14.2 勾股定理的应用
图片预览



文档简介
课件45张PPT。勾股定理
的应用黔江区舟白中学--粟永镇 E-Mail:416352289@qq.com1. 一小船先向正南行进了80米到另一小船处借东西,之后又向正东行进了150米,此时它距出发地多少米?解:设它距出发地x米,
由勾股定理得:
x2=802+1502
=28900
=1702,
解得:x=170
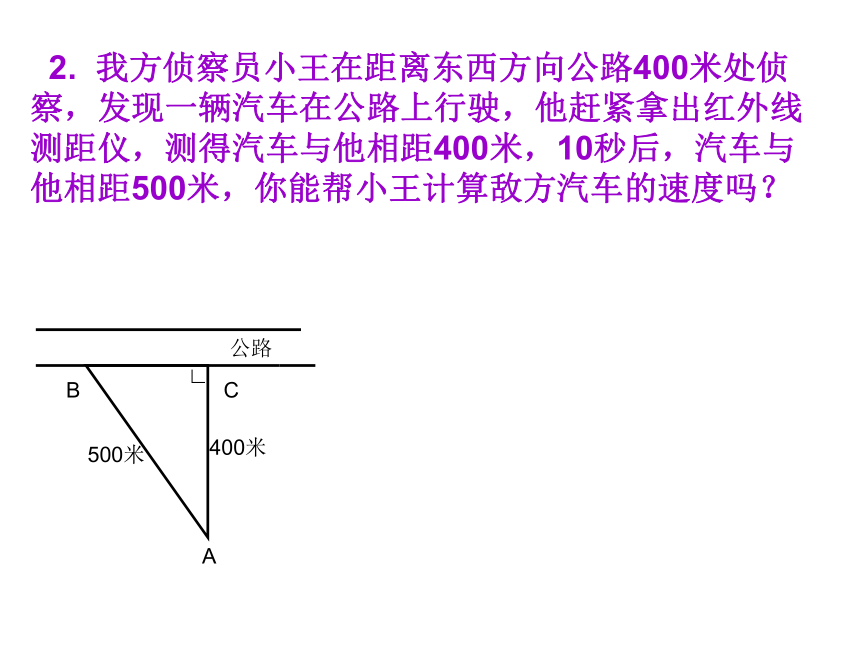
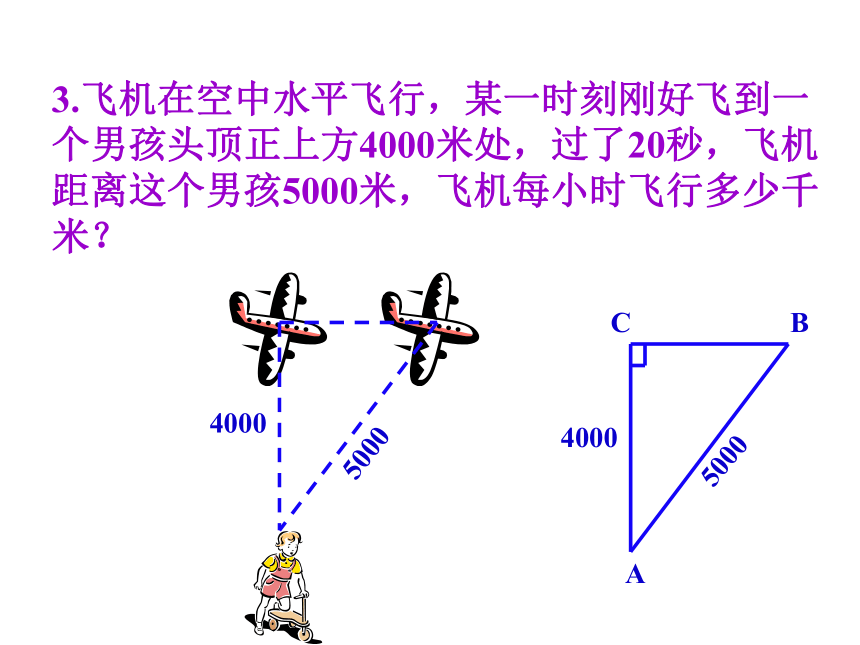
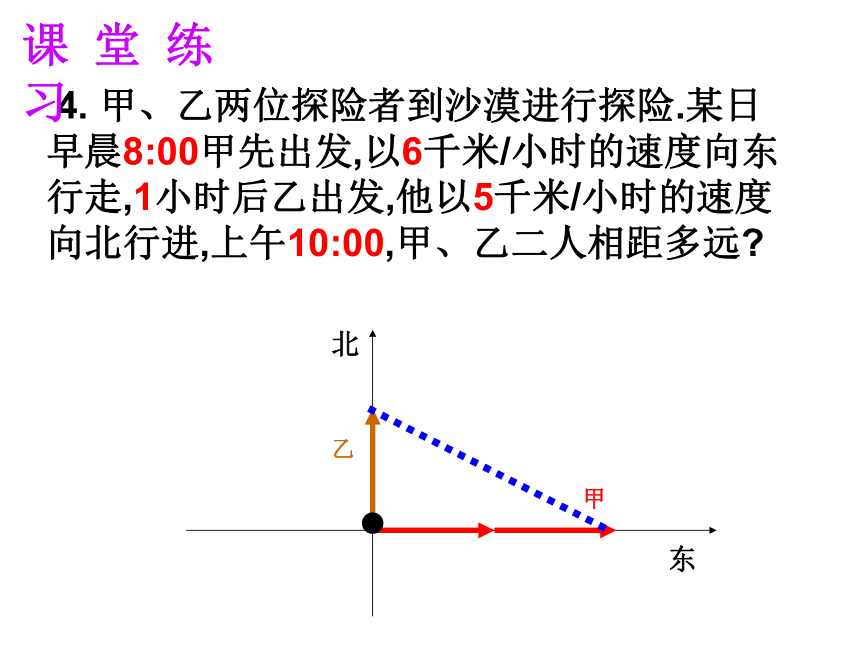
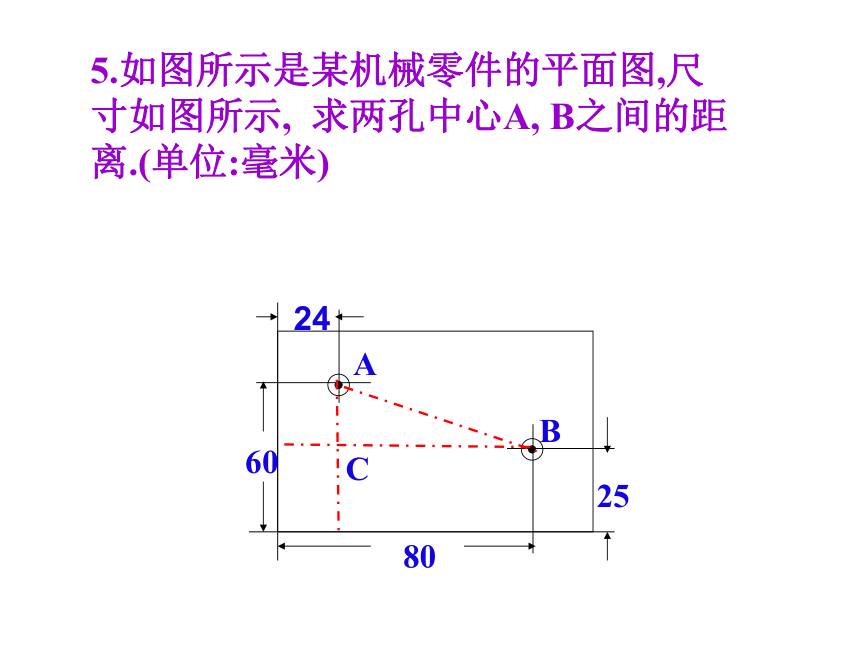
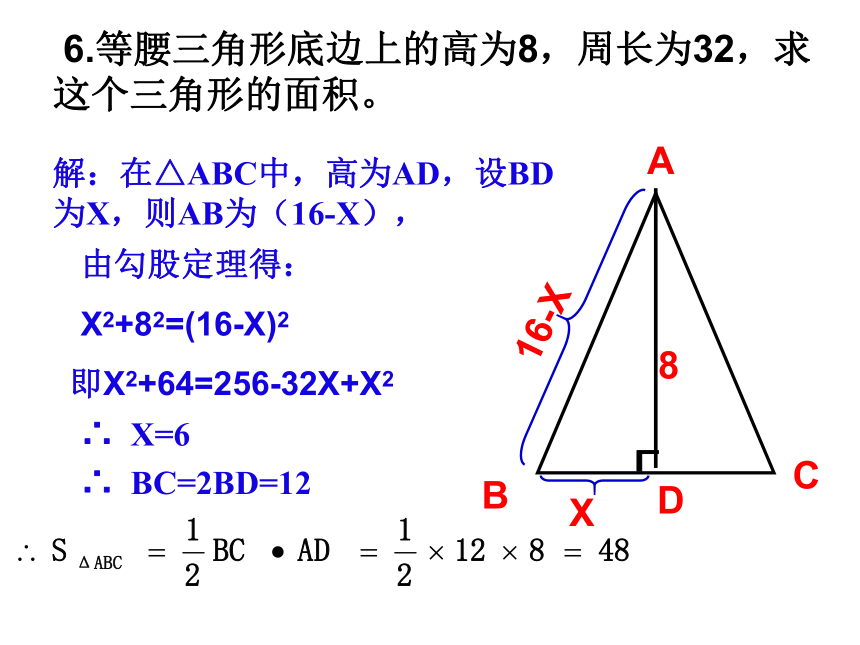
此时小船距出发点170米.勾股定理的应用 2. 我方侦察员小王在距离东西方向公路400米处侦察,发现一辆汽车在公路上行驶,他赶紧拿出红外线测距仪,测得汽车与他相距400米,10秒后,汽车与他相距500米,你能帮小王计算敌方汽车的速度吗?3.飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩5000米,飞机每小时飞行多少千米?40005000 4. 甲、乙两位探险者到沙漠进行探险.某日早晨8:00甲先出发,以6千米/小时的速度向东行走,1小时后乙出发,他以5千米/小时的速度向北行进,上午10:00,甲、乙二人相距多远?东北甲乙课 堂 练 习C5.如图所示是某机械零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米) 6.等腰三角形底边上的高为8,周长为32,求这个三角形的面积。解:在△ABC中,高为AD,设BD为X,则AB为(16-X), 由勾股定理得:
X2+82=(16-X)2即X2+64=256-32X+X2∴ X=6∴ BC=2BD=12我怎么走
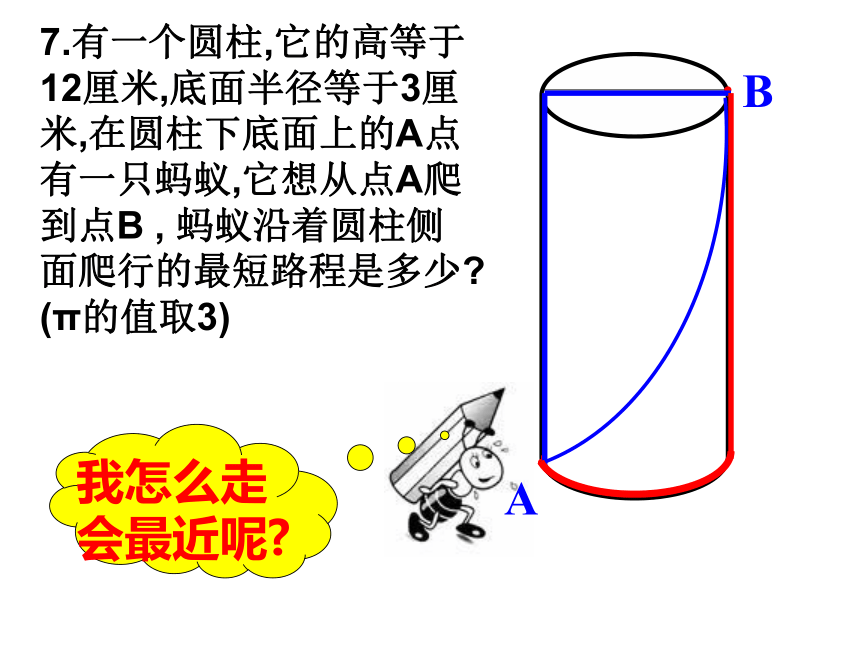
会最近呢?7.有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少? (π的值取3) 高
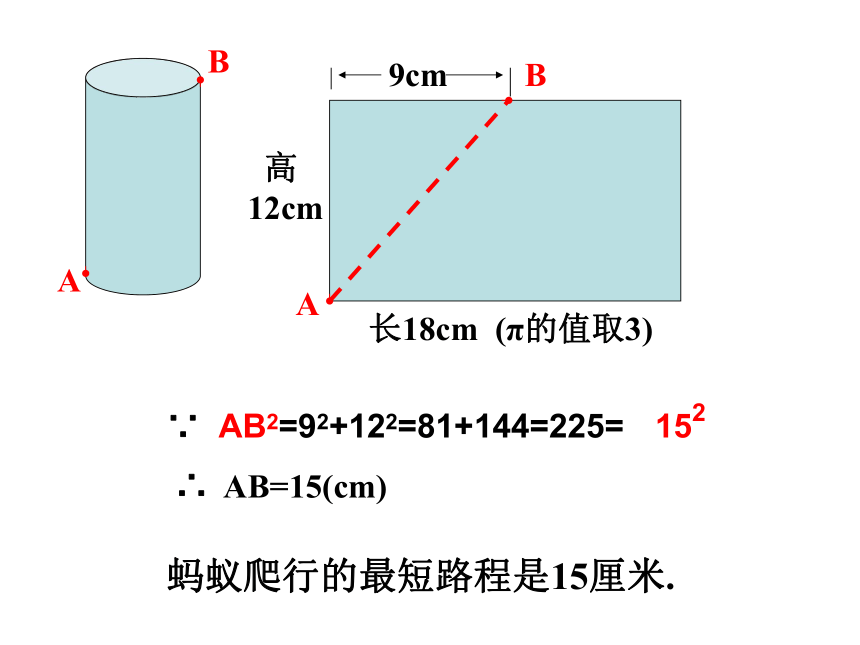
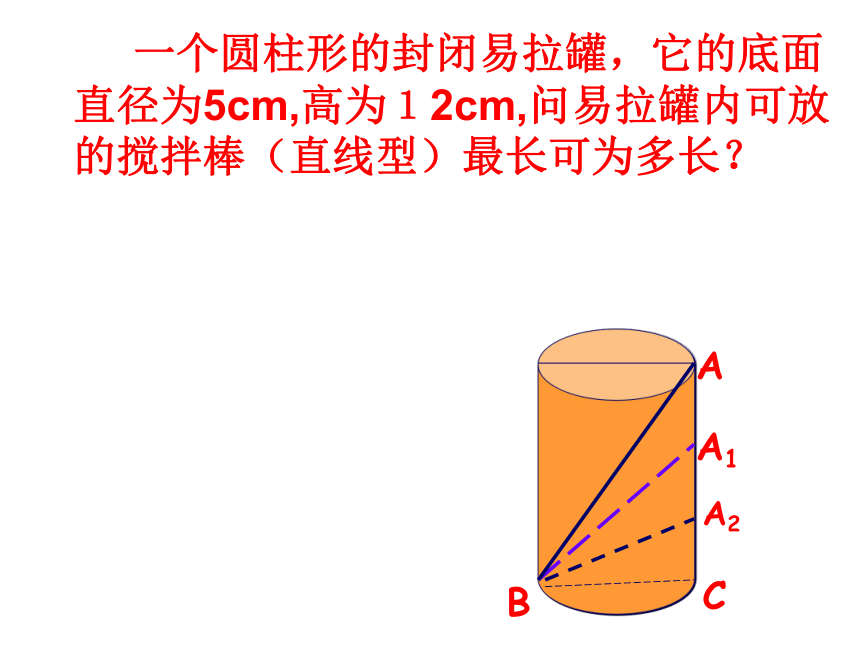
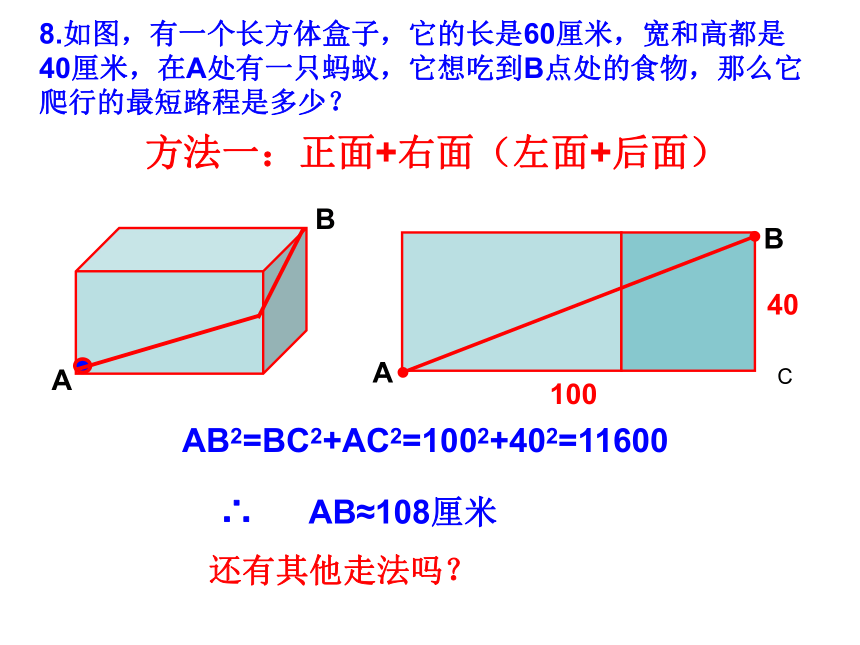
12cmBA长18cm (π的值取3)∵ AB2=92+122=81+144=225=∴ AB=15(cm)蚂蚁爬行的最短路程是15厘米.152 一个圆柱形的封闭易拉罐,它的底面直径为5cm,高为12cm,问易拉罐内可放的搅拌棒(直线型)最长可为多长?BAA1A2C8.如图,有一个长方体盒子,它的长是60厘米,宽和高都是40厘米,在A处有一只蚂蚁,它想吃到B点处的食物,那么它爬行的最短路程是多少?C10040AB2=BC2+AC2=1002+402=11600∴ AB≈108厘米还有其他走法吗?方法一:正面+右面(左面+后面)8.如图,有一个长方体盒子,它的长是60厘米,宽和高都是40厘米,在A处有一只蚂蚁,它想吃到B点处的食物,那么它爬行的最短路程是多少?AB2=AC2+BC2=602+802=1002∴ 蚂蚁爬行的最短路程为100厘米。方法二:正面+上面方法三:左面+上面
自己计算一下9.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200米,结果他在水中实际游了520米,求该河流的宽度。∵AC2=AB2+BC2∴AB2=AC2-BC2
=5202-2002
=4802河流的宽度为480米。10.如果梯子的底端离建筑物9米,那么15米长的梯子可以到达建筑物的高度是多少?X2=152-92
=122∴梯子可以到达建筑物的高度是12米。11.为得到湖两岸A点和B 点间的距离,一个观察者在C点设桩,使△ABC为直角三角形,并测得AC长20米、BC长16米。A,B两点间距离是多少?CAB2=AC2-BC2=202-162=122∴A,B两点距离是12米。12.如图,带阴影的矩形面积是多少?xX2=152+82=172∴ x=1713.有一个水池,在离水池中岸边5尺远有一根新生的芦苇,它高出水面1尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?x2 + 52 = (x+1)2x = 12水池生活中的数学问题 一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?探究所以木板能从门框内通过。 连接AC.在Rt△ABC中,根据勾股定理,得因为AC大于木板的宽, 所以1mABO32.5CD 如图,一个三米长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?要求梯子的底端是否滑动0.5m,只需求出BD的长是否为0.5米。由图可知BD=OD-OB.则需先求出OD,OB的长。所以梯子的顶端下滑0.5m,它的底端不是滑动0.5m.解:如图,在Rt△COD中问题解决问题情境 某楼房三楼失火,消防队员赶来救火,了解到每层楼高3米,消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队员能否进入三楼灭火? 数轴上的点有的表示有理数,有的表示
无理数,你能在数轴上画出表示 的
点吗?01234解:LAB2C试
一
试1请你在作业纸上画图,在数轴上表示 的点2请同学们归纳出如何在数轴上画出表示 的点的方法?3你能在数轴上表示 的点吗?试一试!扩展利用勾股定理作出长为
的线段.11用同样的方法,你能否在数轴上画出表示
,…用同样的方法,你能否在数轴上画出表示
,…02 1 3 54 1 如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA55cm10cm6cm55cm48cm一辆高3米,宽2.4 米的卡车要通过一个半径为3.6米的半圆形隧道,它能顺利通过吗?OA1.2米CD3.6米BAB2=3.62-1.22=12.96-1.44= 11.52∵11.52>32所以卡车能通过 2.3米2米ABCODH在直角三角形OCD中,OC=1 OD=0.8CD2=OC2-OD2=12-0.82
=0.36∴CD=0.6CH=2.3+0.6=2.9∵2.9>2.5∴能通过 一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门? 如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。24平方米如图,以Rt△ABC的三边为边向外作正方形,其面积分别为,请同学们想一想之间有何关系呢?ABCabc + =a2+b2 =c2∵a2+b2=c2∵ a2+b2 =c2
∴ S3=S2+S1探究下面三个圆面积之间的关系abc探究S1、S2、S3之间的关系S1=由勾股定理得 a2+b2=c2∴S1+S2=S3如图6,Rt△ABC中,AC=8,BC=6,∠C=90°,分别以AB、BC、AC为直径作三个半圆,那么阴影部分的面积为 S影阴=SAC+SBC+S△ABC-SAB已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为多少?A为了丰富少年儿童的业余生活,某社区要在如图7所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?如图:边长为4的正方形ABCD中,F是DC的中
点,且CE= BC,则AF⊥EF,试说明理由解:连接AE
∵ABCD是正方形,边长是4,F是DC的中点,EC=1/4BC∴根据勾股定理,在
Rt△ADF,AF2=AD2+DF2=20
Rt△EFC,EF2=EC2+FC2=5
Rt△ABE,AE2=AB2+BE2=25∴AD=4,DF=2,FC=2,EC=1∴AE2=EF2+AF2 ∴∠AEF=90°即AF ⊥EFbca如图大正方形的面积为13,小正方形的面积为1,求(a+b)2的值a2+b2=13(a+b)2=a2+b2+2ab 如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B) √5 (C)2 (D)1分析: 由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图).C2 矩形的一边长是5,对角线是13,则它的面积是 。知 识 回 顾3.三角形三边长分别为6、8、10,那么它最短边上的高为______.
4.测得一个三角形花坛的三边长分别为5cm,12cm,13cm,则这个花坛的面积是________.
5.直角三角形三边是连续整数,则这三角形的各边分别为___6.一个三角形的三边的比为5∶12∶13,它的周长为60cm,则它的面积是___.7.在Rt△ABC中,斜边AB=2,
则AB 2+BC 2+CA 2=___.8.在△ABC中∠C=90°,AB=10,AC=6,则另一边BC=________,面积为______AB边上的高为________;9.等腰△ABC的面积为12cm2,底上的高AD=3cm,则它的周长为___ 10. 若一个直角三角形两条直角边长是3和2,那么第三条边长是多少? 11.若一个直角三角形两条边长是3和2,那么第三条边长是多少?
的应用黔江区舟白中学--粟永镇 E-Mail:416352289@qq.com1. 一小船先向正南行进了80米到另一小船处借东西,之后又向正东行进了150米,此时它距出发地多少米?解:设它距出发地x米,
由勾股定理得:
x2=802+1502
=28900
=1702,
解得:x=170
此时小船距出发点170米.勾股定理的应用 2. 我方侦察员小王在距离东西方向公路400米处侦察,发现一辆汽车在公路上行驶,他赶紧拿出红外线测距仪,测得汽车与他相距400米,10秒后,汽车与他相距500米,你能帮小王计算敌方汽车的速度吗?3.飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩5000米,飞机每小时飞行多少千米?40005000 4. 甲、乙两位探险者到沙漠进行探险.某日早晨8:00甲先出发,以6千米/小时的速度向东行走,1小时后乙出发,他以5千米/小时的速度向北行进,上午10:00,甲、乙二人相距多远?东北甲乙课 堂 练 习C5.如图所示是某机械零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米) 6.等腰三角形底边上的高为8,周长为32,求这个三角形的面积。解:在△ABC中,高为AD,设BD为X,则AB为(16-X), 由勾股定理得:
X2+82=(16-X)2即X2+64=256-32X+X2∴ X=6∴ BC=2BD=12我怎么走
会最近呢?7.有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少? (π的值取3) 高
12cmBA长18cm (π的值取3)∵ AB2=92+122=81+144=225=∴ AB=15(cm)蚂蚁爬行的最短路程是15厘米.152 一个圆柱形的封闭易拉罐,它的底面直径为5cm,高为12cm,问易拉罐内可放的搅拌棒(直线型)最长可为多长?BAA1A2C8.如图,有一个长方体盒子,它的长是60厘米,宽和高都是40厘米,在A处有一只蚂蚁,它想吃到B点处的食物,那么它爬行的最短路程是多少?C10040AB2=BC2+AC2=1002+402=11600∴ AB≈108厘米还有其他走法吗?方法一:正面+右面(左面+后面)8.如图,有一个长方体盒子,它的长是60厘米,宽和高都是40厘米,在A处有一只蚂蚁,它想吃到B点处的食物,那么它爬行的最短路程是多少?AB2=AC2+BC2=602+802=1002∴ 蚂蚁爬行的最短路程为100厘米。方法二:正面+上面方法三:左面+上面
自己计算一下9.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200米,结果他在水中实际游了520米,求该河流的宽度。∵AC2=AB2+BC2∴AB2=AC2-BC2
=5202-2002
=4802河流的宽度为480米。10.如果梯子的底端离建筑物9米,那么15米长的梯子可以到达建筑物的高度是多少?X2=152-92
=122∴梯子可以到达建筑物的高度是12米。11.为得到湖两岸A点和B 点间的距离,一个观察者在C点设桩,使△ABC为直角三角形,并测得AC长20米、BC长16米。A,B两点间距离是多少?CAB2=AC2-BC2=202-162=122∴A,B两点距离是12米。12.如图,带阴影的矩形面积是多少?xX2=152+82=172∴ x=1713.有一个水池,在离水池中岸边5尺远有一根新生的芦苇,它高出水面1尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?x2 + 52 = (x+1)2x = 12水池生活中的数学问题 一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?探究所以木板能从门框内通过。 连接AC.在Rt△ABC中,根据勾股定理,得因为AC大于木板的宽, 所以1mABO32.5CD 如图,一个三米长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?要求梯子的底端是否滑动0.5m,只需求出BD的长是否为0.5米。由图可知BD=OD-OB.则需先求出OD,OB的长。所以梯子的顶端下滑0.5m,它的底端不是滑动0.5m.解:如图,在Rt△COD中问题解决问题情境 某楼房三楼失火,消防队员赶来救火,了解到每层楼高3米,消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队员能否进入三楼灭火? 数轴上的点有的表示有理数,有的表示
无理数,你能在数轴上画出表示 的
点吗?01234解:LAB2C试
一
试1请你在作业纸上画图,在数轴上表示 的点2请同学们归纳出如何在数轴上画出表示 的点的方法?3你能在数轴上表示 的点吗?试一试!扩展利用勾股定理作出长为
的线段.11用同样的方法,你能否在数轴上画出表示
,…用同样的方法,你能否在数轴上画出表示
,…02 1 3 54 1 如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA55cm10cm6cm55cm48cm一辆高3米,宽2.4 米的卡车要通过一个半径为3.6米的半圆形隧道,它能顺利通过吗?OA1.2米CD3.6米BAB2=3.62-1.22=12.96-1.44= 11.52∵11.52>32所以卡车能通过 2.3米2米ABCODH在直角三角形OCD中,OC=1 OD=0.8CD2=OC2-OD2=12-0.82
=0.36∴CD=0.6CH=2.3+0.6=2.9∵2.9>2.5∴能通过 一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门? 如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。24平方米如图,以Rt△ABC的三边为边向外作正方形,其面积分别为,请同学们想一想之间有何关系呢?ABCabc + =a2+b2 =c2∵a2+b2=c2∵ a2+b2 =c2
∴ S3=S2+S1探究下面三个圆面积之间的关系abc探究S1、S2、S3之间的关系S1=由勾股定理得 a2+b2=c2∴S1+S2=S3如图6,Rt△ABC中,AC=8,BC=6,∠C=90°,分别以AB、BC、AC为直径作三个半圆,那么阴影部分的面积为 S影阴=SAC+SBC+S△ABC-SAB已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为多少?A为了丰富少年儿童的业余生活,某社区要在如图7所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?如图:边长为4的正方形ABCD中,F是DC的中
点,且CE= BC,则AF⊥EF,试说明理由解:连接AE
∵ABCD是正方形,边长是4,F是DC的中点,EC=1/4BC∴根据勾股定理,在
Rt△ADF,AF2=AD2+DF2=20
Rt△EFC,EF2=EC2+FC2=5
Rt△ABE,AE2=AB2+BE2=25∴AD=4,DF=2,FC=2,EC=1∴AE2=EF2+AF2 ∴∠AEF=90°即AF ⊥EFbca如图大正方形的面积为13,小正方形的面积为1,求(a+b)2的值a2+b2=13(a+b)2=a2+b2+2ab 如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B) √5 (C)2 (D)1分析: 由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图).C2 矩形的一边长是5,对角线是13,则它的面积是 。知 识 回 顾3.三角形三边长分别为6、8、10,那么它最短边上的高为______.
4.测得一个三角形花坛的三边长分别为5cm,12cm,13cm,则这个花坛的面积是________.
5.直角三角形三边是连续整数,则这三角形的各边分别为___6.一个三角形的三边的比为5∶12∶13,它的周长为60cm,则它的面积是___.7.在Rt△ABC中,斜边AB=2,
则AB 2+BC 2+CA 2=___.8.在△ABC中∠C=90°,AB=10,AC=6,则另一边BC=________,面积为______AB边上的高为________;9.等腰△ABC的面积为12cm2,底上的高AD=3cm,则它的周长为___ 10. 若一个直角三角形两条直角边长是3和2,那么第三条边长是多少? 11.若一个直角三角形两条边长是3和2,那么第三条边长是多少?
