第5单元完美的图形 圆练习卷 小学数学六年级上册青岛版(含答案)
文档属性
| 名称 | 第5单元完美的图形 圆练习卷 小学数学六年级上册青岛版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 00:00:00 | ||
图片预览




文档简介
第5单元完美的图形-圆练习卷-小学数学六年级上册青岛版
一、选择题
1.圆的直径增加4分米,周长增加( )分米。
A.3.14 B.6.28 C.12.56 D.25.12
2.在推导圆的面积公式时,把一个圆分成若干(偶数)等份后,拼成一个近似长方形,这个长方形的长近似于( )。
A.圆的半径 B.圆的周长 C.圆周长的
3.下面3个正方形的边长都是8厘米,每个图中阴影的面积( )。
A.第一个最大 B.相等 C.不相等 D.无法判断
4.一张圆形的纸,用对折的方法确定圆心,至少要对折( )次。
A.1 B.2 C.3
5.在一张长8cm、宽2cm的长方形纸上,最多可剪出( )个半径是1cm的圆。
A.2 B.4 C.8 D.16
6.如图,圆面积与正方形面积的比是( )。
A. B. C.
7.一个正方形和一个圆的周长都是25.12厘米,它们的面积( )。
A.相等 B.圆的面积大 C.正方形面积大
8.如图,长方形的面积等于圆的面积,圆的半径为r,阴影部分的面积是( )。
A.πr2 B.πr2 C.πr2 D.πr2
二、填空题
9.在篝火晚会中,同学们总会自然而然地围成一个圆,这是因为( )。
10.把一个半径是5厘米的圆分成若干等份,剪开后,照下图的样子拼起来,拼成图形的周长比原来圆的周长增加了( )厘米;拼成图形的面积是( )平方厘米。
11.将一个圆等分成若干份(如图),拼成一个近似的长方形,圆的面积是( )cm2。
12.如下图所示,阴影部分的周长是( )厘米,面积是( )平方厘米。
13.如图,一棵树干周长是125.6cm,树干的横截面积约是( )。
14.用一根长26分米的铁丝围成一个圆,接头处长0.88分米,这个圆的面积是( )平方分米。
15.在推导圆的面积公式时,把一个圆平均分成若干等份,然后再拼成一个近似的长方形,这是用了数学上的( )思想。如果拼成的长方形的长是12.56cm,原来圆的面积是( )平方厘米。
16.阴影部分的面积是25平方厘米,则圆环的面积是( )平方厘米。
三、判断题
17.半径是2厘米的圆,面积和周长相等。( )
18.两圆半径的比是2∶1,则其周长的也是2∶1。( )
19.一个圆的半径增加1厘米,它的周长就增加6.28厘米(π取3.14)。( )
20.圆有无数条对称轴,圆的对称轴是它的直径,而一个半圆却只有一条对称轴。( )
21.一个圆的半径扩大3倍,周长扩大3倍,面积也扩大3倍。( )
四、图形计算
22.求阴影部分的面积。
23.求阴影部分面积。
五、解答题
24.公园中有一个近似于圆形的湖,直径为100米。
(1)这个湖的水面面积是多少平方米?
(2)如果妙妙每分钟步行52米,她绕湖周大约用多长时间?(得数保留整数)
25.某小区里有一个圆形花坛,在花坛的外沿安了100个地灯。每两个地灯之间的距离是1.57米。这个圆形花坛的半径是多少米?
26.希望小学有一个直径是8米的圆形花坛。为美化校园,把这个花坛进行了扩建,扩建后花坛的直径与原来直径的比是3∶2。扩建后花坛的面积增加了多少平方米?
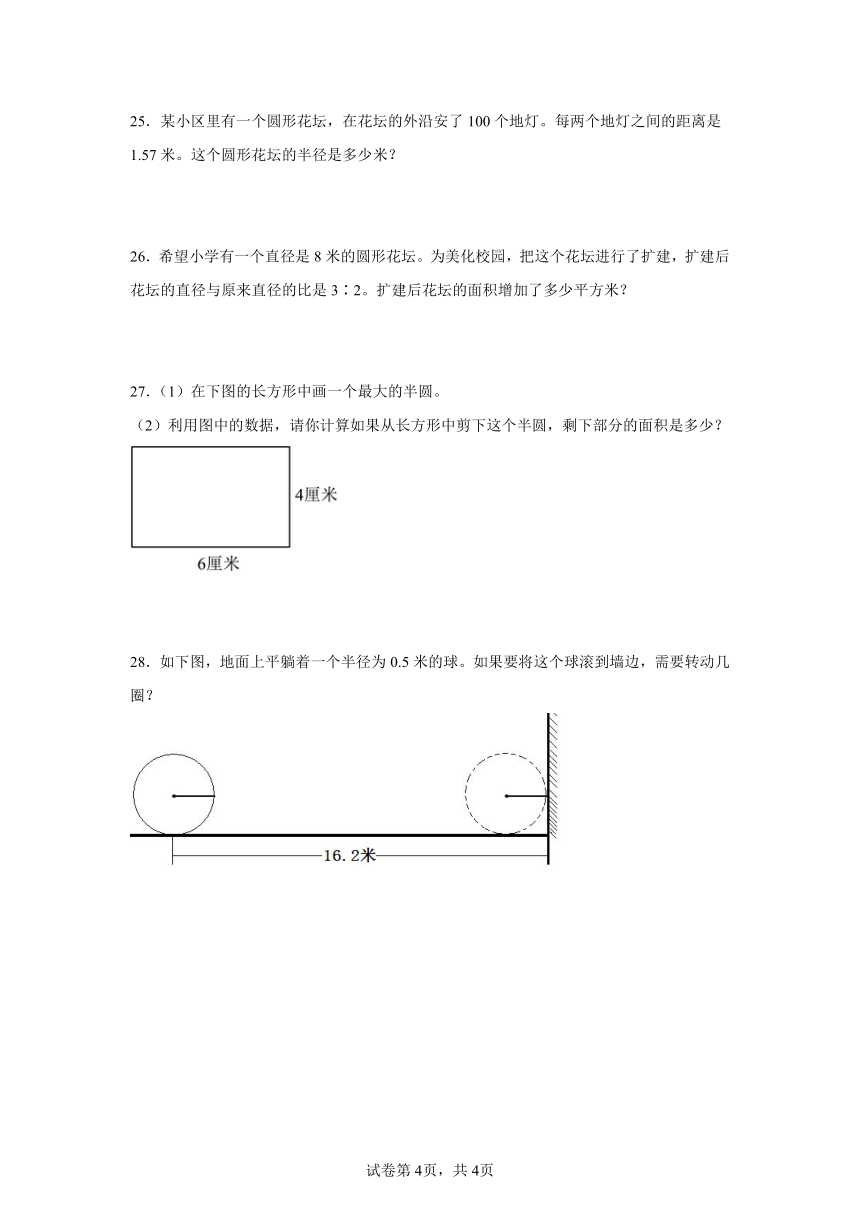
27.(1)在下图的长方形中画一个最大的半圆。
(2)利用图中的数据,请你计算如果从长方形中剪下这个半圆,剩下部分的面积是多少?
28.如下图,地面上平躺着一个半径为0.5米的球。如果要将这个球滚到墙边,需要转动几圈?
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】假设原来的直径是1分米,则增加4分米后,此时的直径:1+4=5分米,根据圆的周长公式:C=πd,求出增加前和增加后的周长,再相减即可。
【详解】假设增加前的直径是1分米
3.14×1=3.14(分米)
1+4=5(分米)
3.14×5=15.7(分米)
15.7-3.14=12.56(分米)
故答案为:C
【点睛】本题主要考查圆的周长公式,熟练掌握它的公式并灵活运用。
2.C
【分析】推导圆的面积公式时,将圆转化成一个近似的长方形,如图:长方形的长相当于圆周长的一半,长方形的宽相当于圆的半径,据此解答即可。
【详解】在推导圆的面积公式时,把一个圆分成若干(偶数)等份后,拼成一个近似长方形,这个长方形的长近似于圆周长的;
故答案为:C。
【点睛】熟练掌握圆的面积推导过程是解答本题的关键。
3.B
【分析】可以利用图形的旋转、拼接等方法,比较空白处的面积大小,进而比较阴影的面积大小。
【详解】图中三个正方形面积相等,通过图形的旋转、拼接等,很容易得出三个正方形中,空白面积相等,即每个图中阴影的面积相等。
故答案为:B
【点睛】圆的面积计算为本题考查重点。
4.B
【分析】圆中心的那个点即圆心,所有直径都相交于圆心,将一个圆形纸片最少要对折两次,才能找到两条折痕相交的那个点,即圆心。
【详解】由分析可得:一张圆形的纸,用对折的方法确定圆心,至少要对折2次。
故答案为:B
【点睛】本题考查了确定圆心的方法。
5.B
【分析】半径是1cm的圆,直径就是2厘米,长方形的宽是2厘米,所以最多可以剪8÷2=4个圆。据此解答。
【详解】8÷(1×2)
=8÷2
=4(个)
故答案为:B
【点睛】本题考查的知识点就是以长方形的宽为圆直径,在长方形最多能剪几个圆的问题。因此求得圆的直径是解答本题的关键。
6.B
【分析】假设圆的半径是r,圆的直径是正方形对角线,根据圆的面积=πr ,正方形面积=对角线×对角线÷2,表示出圆和正方形面积,写出面积比,化简即可。
【详解】(πr )∶(2r×2r÷2)
=(πr )∶(2r )
=π∶2
故答案为:B
【点睛】关键是掌握圆和正方形面积求法,理解比的意义。
7.B
【分析】周长相等的情况下,圆的面积大于其它的平面图形。据此解题。
【详解】一个正方形和一个圆的周长都是25.12厘米,此时,圆的面积大于正方形的面积。
故答案为:B
【点睛】本题考查了圆和正方形的面积,明确圆面积的特点是解题的关键。
8.B
【分析】由圆的面积公式:S=πr2,可知:圆的面积是πr2;又长方形的面积等于圆的面积,所以长方形的面积也是πr2;长方形中,空白部分是圆的面积,用长方形的面积-圆的面积=阴影部分的面积;据此解答。
【详解】长方形的面积=圆的面积=πr2
阴影部分的面积=长方形的面积-圆的面积=πr2-πr2=πr2
故答案为:B
【点睛】本题主要考查圆的面积公式的灵活运用。
9.在同一个圆中,半径都相等
【分析】根据圆的特点,在同一个圆中,半径都相等,同学们总会自然而然地围成一个圆,则每位同学到篝火的距离是一样的,据此填空即可。
【详解】由分析可知:
在篝火晚会中,同学们总会自然而然地围成一个圆,这是因为在同一个圆中,半径都相等。
【点睛】本题考查圆的特点,明确圆的特点是解题的关键。
10. 10 78.5
【分析】由图可知,拼成图形的周长比圆的周长多2条半径的长度,拼成图形的面积等于圆的面积,利用“”求出圆的面积,据此解答。
【详解】增加的周长:5×2=10(厘米)
面积:3.14×52
=3.14×25
=78.5(平方厘米)
【点睛】掌握圆的面积计算公式是解答题目的关键。
11.12.56
【分析】根据题意可知,拼成的近似长方形的长等于圆的周长的一半;根据圆的周长公式:π×2×半径,求出半径;再根据圆的面积公式:π×半径2,代入数据,即可解答。
【详解】长方形的宽:6.28×2÷3.14÷2
=12.56÷3.14÷2
=4÷2
=2(厘米)
面积:3.14×22
=3.14×4
=12.56(平方厘米)
【点睛】本题考查圆的周长公式和面积公式的应用,关键数明确拼成的近似长方形的长等于圆的周长的一半,进而求出圆的半径。
12. 25.12 25.12
【分析】观察图形可知,阴影部分的周长等于半径为4cm圆的周长的一半加上直径为4cm圆的周长;根据圆的周长公式:π×2×半径,代入数据,求出阴影部分周长;下半部分阴影与上部分空白处相等,阴影部分面积等于半径为4cm圆的面积的一半;根据圆的面积公式:π×半径2,代入数据,即可解答。
【详解】周长:3.14×2×4÷2+3.14×4
=6.28×4÷2+12.56
=25.12÷2+12.56
=12.56+12.56
=25.12(厘米)
面积:3.14×42÷2
=3.14×16÷2
=50.24÷2
=25.12(平方厘米)
【点睛】本题考查阴影部分的的周长和面积的求法,以及圆的周长公式、面积公式的应用,关键数熟记公式。
13.1256cm2
【分析】根据圆的周长公式:周长=π×2×半径;半径=周长÷π÷2,代入数据,求出树干的半径;再根据圆的面积公式:面积=π×半径2,代入数据,即可解答。
【详解】半径:125.6÷3.14÷2
=40÷2
=20(cm)
面积:3.14×202
=3.14×400
=1256(cm2)
【点睛】本题考查圆的周长公司、面积公式的应用,关键是熟记公式,灵活运用。
14.50.24
【分析】由题意可知:圆的周长是26-0.88=25.12分米,带入圆的周长公式即可求出圆的半径,再将半径值带入圆的面积公式即可解答。
【详解】(26-0.88)÷3.14÷2
=25.12÷3.14÷2
=4(分米)
3.14×42=50.24(平方分米)
【点睛】本题主要考查圆的周长、面积公式的灵活运用,求出半径值是解题的关键。
15. 转化 50.24
【分析】在推导圆的面积公式时,把一个圆平均分成若干等份,然后再拼成一个近似的长方形,将求圆的面积转化为求长方形的面积,是运用转化思想;拼成的长方形的长是圆周长的一半,根据圆的周长公式求出圆的半径,再带入圆的面积公式计算即可。
【详解】在推导圆的面积公式时,把一个圆平均分成若干等份,然后再拼成一个近似的长方形,这是用了数学上的转化思想。
12.56×2÷3.14÷2
=25.12÷3.14÷2
=8÷2
=4(厘米)
3.14×42=50.24(平方厘米)
【点睛】明确将圆拼成近似的长方形时长方形的长是圆周长的一半是解题的关键。
16.157
【分析】由图知:阴影部分的面积是以大圆半径为直角边的三角形面积减以小圆半径为直角边的三角形面积,也就是大圆的半径平方减小圆半径的平方等于25×2=50平方厘米。又据圆环的面积=(大圆半径平方-小圆半径平方)×3.14=50×3.14,据此计算出积即求得圆环面积。
【详解】25×2=50(平方厘米)
50×3.14=157(平方厘米)
【点睛】理解大圆半径平方与小圆半径平方差是50平方厘米,带入圆环面积公式是解答此题的关键。
17.×
【分析】面积与周长的定义不同:圆的表面或围成的圆形表面的大小,叫做圆的面积;围成圆的一周的长度叫做这个圆的周长;所采用的计量单位也不同:此题中,周长的单位是厘米,面积的单位是平方厘米,单位不能统一,所以没法比较它们的大小。只能说半径是2厘米的圆的周长和面积的数据相等。
【详解】圆的周长:2×3.14×2=12.56(厘米)
圆的面积:3.14×22
=3.14×4
=12.56(平方厘米)
可见圆的周长和圆的面积虽然得出的数据一样,但计算方法不一样,单位不一样,表达的意义也不一样,所以面积和周长无法比较。
故答案为:×
【点睛】此题的解题关键是充分理解圆的面积和周长的意义。这里要注意:单位不能统一的数据无法比较它们的大小。
18.√
【分析】根据题意,可设两圆的半径分别为2,1,那么根据圆的周长公式C=2πr进行计算,然后再进行比较即可得到答案。
【详解】设两圆的半径分别为2、1,
两个圆周长的比为:
(3.14×2×2):∶(3.14×2×1)
=12.56∶6.28
=2∶1
故答案:√
【点睛】此题主要考查的是圆半径与周长的关系,解答此题关键是掌握两个圆半径的比等于两个圆的周长的比。
19.√
【分析】设圆的半径是,按周长公式,计算出现在的周长,减去以前的周长,判断答案是否正确。
【详解】
故答案为:√
【点睛】此类问题可以把圆的半径用相应的数字或字母代替,然后利用圆的周长公式表示出圆的周长进行解答。
20.×
【分析】将图形沿着一条直线对折,如果直线两侧的部分能够完全重合,折痕所在的直线叫做它的对称轴,圆的直径是一条线段不是圆的对称轴,直径所在的直线是圆的对称轴;据此解答。
【详解】圆形的对称轴:每条直径所在的直线,圆有无数条对称轴;半圆的对称轴:圆心和弧中点连线所在的直线,半圆只有1条对称轴。
故答案为:×
【点睛】掌握对称轴的意义是解答题目的关键。
21.×
【分析】圆的周长=2πr,圆的面积=πr2。根据积的变化规律,如果一个因数扩大(或缩小)若干倍,另一个因数不变,那么积也扩大(或缩小)相同倍数,则圆的半径扩大3倍,周长也扩大3倍,面积扩大3×3=9倍。
【详解】一个圆的半径扩大3倍,周长也扩大3倍,面积扩大9倍。
故答案为:×
【点睛】本题考查圆的周长、面积公式和积的变化规律的综合应用。
22.3.87平方厘米
【分析】由图可知,阴影部分的面积=长方形的面积-半圆的面积。
【详解】6×(6÷2)-×3.14×(6÷2)2
=6×3-×3.14×9
=18-1.57×9
=18-14.13
=3.87(平方厘米)
23.251.2平方厘米
【分析】阴影部分是一个圆环,圆环的面积=π(R2-r2),据此解答。
【详解】3.14×(122-82)
=3.14×(144-64)
=3.14×80
=251.2(平方厘米)
24.(1)7850平方米
(2)6分钟
【分析】(1)根据圆的面积公式:S=πr2,据此代入数值进行计算即可;
(2)根据圆的周长公式:C=πd,据此求出湖的一周的长度,再根据路程÷速度=时间,据此解答即可。
【详解】(1)3.14×(100÷2)2
=3.14×2500
=7850(平方米)
答:这个湖的水面面积是7850平方米。
(2)
=314÷52
≈6(分钟)
答:她绕湖周大约用了6分钟。
【点睛】本题考查圆的周长和面积,熟记公式是解题的关键。
25.25米
【分析】由于圆形花坛是封闭图形,则间距数=棵树,由此即可知道间距数是100,由于1个间距是1.57米,则这个圆形花坛的周长:1.57×100=157米,根据圆的周长公式:C=2πr,把数代入即可求出半径。
【详解】1.57×100=157(米)
157÷3.14÷2
=50÷2
=25(米)
答:这个圆形花坛的半径是25米。
【点睛】本题主要考查植树问题以及圆的周长公式,熟练掌握圆的周长公式并灵活运用。
26.62.8平方米
【分析】由“扩建后花坛的直径与原来直径的比是3∶2”可知:扩建后的直径是原来直径的,原来的直径已知,从而可以求出扩建后的直径,进而可以求出扩建前后花坛的面积,再求差即可。
【详解】扩建后的直径:8×=12(米)
增加的面积:3.14×(12÷2)2-3.14×(8÷2)2
=3.14×(36-16)
=3.14×20
=62.8(平方米)
答:扩建后花坛的面积增加了62.8平方米。
【点睛】解答此题的关键是利用直径比求出扩建后的直径。
27.(1)见详解
(2)9.87平方厘米
【分析】(1)由于画一个半圆,则半圆的直径最大是6厘米,由此即可画图;
(2)根据半圆的面积公式:S=πr2÷2,以及长方形的面积公式,长×宽,用长方形的面积减去半圆的面积即可求解。
【详解】(1)如图所示
(2)3.14×(6÷2)2÷2
=3.14×9÷2
=28.26÷2
=14.13(平方厘米)
4×6-14.13
=24-14.13
=9.87(平方厘米)
答:剩下部分的面积是9.87平方厘米
【点睛】本题主要考查圆的面积公式以及长方形的面积公式,熟练掌握它们的公式并灵活运用。
28.5圈
【分析】根据圆的周长=2πr,求出球的周长,用滚动距离÷周长即可。
【详解】(16.2-0.5)÷(2×3.14×0.5)
=15.7÷3.14
=5(圈)
答:需要转动5圈。
【点睛】明确滚动的总路程是(16.2-0.5)米是解决本题的关键。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.圆的直径增加4分米,周长增加( )分米。
A.3.14 B.6.28 C.12.56 D.25.12
2.在推导圆的面积公式时,把一个圆分成若干(偶数)等份后,拼成一个近似长方形,这个长方形的长近似于( )。
A.圆的半径 B.圆的周长 C.圆周长的
3.下面3个正方形的边长都是8厘米,每个图中阴影的面积( )。
A.第一个最大 B.相等 C.不相等 D.无法判断
4.一张圆形的纸,用对折的方法确定圆心,至少要对折( )次。
A.1 B.2 C.3
5.在一张长8cm、宽2cm的长方形纸上,最多可剪出( )个半径是1cm的圆。
A.2 B.4 C.8 D.16
6.如图,圆面积与正方形面积的比是( )。
A. B. C.
7.一个正方形和一个圆的周长都是25.12厘米,它们的面积( )。
A.相等 B.圆的面积大 C.正方形面积大
8.如图,长方形的面积等于圆的面积,圆的半径为r,阴影部分的面积是( )。
A.πr2 B.πr2 C.πr2 D.πr2
二、填空题
9.在篝火晚会中,同学们总会自然而然地围成一个圆,这是因为( )。
10.把一个半径是5厘米的圆分成若干等份,剪开后,照下图的样子拼起来,拼成图形的周长比原来圆的周长增加了( )厘米;拼成图形的面积是( )平方厘米。
11.将一个圆等分成若干份(如图),拼成一个近似的长方形,圆的面积是( )cm2。
12.如下图所示,阴影部分的周长是( )厘米,面积是( )平方厘米。
13.如图,一棵树干周长是125.6cm,树干的横截面积约是( )。
14.用一根长26分米的铁丝围成一个圆,接头处长0.88分米,这个圆的面积是( )平方分米。
15.在推导圆的面积公式时,把一个圆平均分成若干等份,然后再拼成一个近似的长方形,这是用了数学上的( )思想。如果拼成的长方形的长是12.56cm,原来圆的面积是( )平方厘米。
16.阴影部分的面积是25平方厘米,则圆环的面积是( )平方厘米。
三、判断题
17.半径是2厘米的圆,面积和周长相等。( )
18.两圆半径的比是2∶1,则其周长的也是2∶1。( )
19.一个圆的半径增加1厘米,它的周长就增加6.28厘米(π取3.14)。( )
20.圆有无数条对称轴,圆的对称轴是它的直径,而一个半圆却只有一条对称轴。( )
21.一个圆的半径扩大3倍,周长扩大3倍,面积也扩大3倍。( )
四、图形计算
22.求阴影部分的面积。
23.求阴影部分面积。
五、解答题
24.公园中有一个近似于圆形的湖,直径为100米。
(1)这个湖的水面面积是多少平方米?
(2)如果妙妙每分钟步行52米,她绕湖周大约用多长时间?(得数保留整数)
25.某小区里有一个圆形花坛,在花坛的外沿安了100个地灯。每两个地灯之间的距离是1.57米。这个圆形花坛的半径是多少米?
26.希望小学有一个直径是8米的圆形花坛。为美化校园,把这个花坛进行了扩建,扩建后花坛的直径与原来直径的比是3∶2。扩建后花坛的面积增加了多少平方米?
27.(1)在下图的长方形中画一个最大的半圆。
(2)利用图中的数据,请你计算如果从长方形中剪下这个半圆,剩下部分的面积是多少?
28.如下图,地面上平躺着一个半径为0.5米的球。如果要将这个球滚到墙边,需要转动几圈?
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】假设原来的直径是1分米,则增加4分米后,此时的直径:1+4=5分米,根据圆的周长公式:C=πd,求出增加前和增加后的周长,再相减即可。
【详解】假设增加前的直径是1分米
3.14×1=3.14(分米)
1+4=5(分米)
3.14×5=15.7(分米)
15.7-3.14=12.56(分米)
故答案为:C
【点睛】本题主要考查圆的周长公式,熟练掌握它的公式并灵活运用。
2.C
【分析】推导圆的面积公式时,将圆转化成一个近似的长方形,如图:长方形的长相当于圆周长的一半,长方形的宽相当于圆的半径,据此解答即可。
【详解】在推导圆的面积公式时,把一个圆分成若干(偶数)等份后,拼成一个近似长方形,这个长方形的长近似于圆周长的;
故答案为:C。
【点睛】熟练掌握圆的面积推导过程是解答本题的关键。
3.B
【分析】可以利用图形的旋转、拼接等方法,比较空白处的面积大小,进而比较阴影的面积大小。
【详解】图中三个正方形面积相等,通过图形的旋转、拼接等,很容易得出三个正方形中,空白面积相等,即每个图中阴影的面积相等。
故答案为:B
【点睛】圆的面积计算为本题考查重点。
4.B
【分析】圆中心的那个点即圆心,所有直径都相交于圆心,将一个圆形纸片最少要对折两次,才能找到两条折痕相交的那个点,即圆心。
【详解】由分析可得:一张圆形的纸,用对折的方法确定圆心,至少要对折2次。
故答案为:B
【点睛】本题考查了确定圆心的方法。
5.B
【分析】半径是1cm的圆,直径就是2厘米,长方形的宽是2厘米,所以最多可以剪8÷2=4个圆。据此解答。
【详解】8÷(1×2)
=8÷2
=4(个)
故答案为:B
【点睛】本题考查的知识点就是以长方形的宽为圆直径,在长方形最多能剪几个圆的问题。因此求得圆的直径是解答本题的关键。
6.B
【分析】假设圆的半径是r,圆的直径是正方形对角线,根据圆的面积=πr ,正方形面积=对角线×对角线÷2,表示出圆和正方形面积,写出面积比,化简即可。
【详解】(πr )∶(2r×2r÷2)
=(πr )∶(2r )
=π∶2
故答案为:B
【点睛】关键是掌握圆和正方形面积求法,理解比的意义。
7.B
【分析】周长相等的情况下,圆的面积大于其它的平面图形。据此解题。
【详解】一个正方形和一个圆的周长都是25.12厘米,此时,圆的面积大于正方形的面积。
故答案为:B
【点睛】本题考查了圆和正方形的面积,明确圆面积的特点是解题的关键。
8.B
【分析】由圆的面积公式:S=πr2,可知:圆的面积是πr2;又长方形的面积等于圆的面积,所以长方形的面积也是πr2;长方形中,空白部分是圆的面积,用长方形的面积-圆的面积=阴影部分的面积;据此解答。
【详解】长方形的面积=圆的面积=πr2
阴影部分的面积=长方形的面积-圆的面积=πr2-πr2=πr2
故答案为:B
【点睛】本题主要考查圆的面积公式的灵活运用。
9.在同一个圆中,半径都相等
【分析】根据圆的特点,在同一个圆中,半径都相等,同学们总会自然而然地围成一个圆,则每位同学到篝火的距离是一样的,据此填空即可。
【详解】由分析可知:
在篝火晚会中,同学们总会自然而然地围成一个圆,这是因为在同一个圆中,半径都相等。
【点睛】本题考查圆的特点,明确圆的特点是解题的关键。
10. 10 78.5
【分析】由图可知,拼成图形的周长比圆的周长多2条半径的长度,拼成图形的面积等于圆的面积,利用“”求出圆的面积,据此解答。
【详解】增加的周长:5×2=10(厘米)
面积:3.14×52
=3.14×25
=78.5(平方厘米)
【点睛】掌握圆的面积计算公式是解答题目的关键。
11.12.56
【分析】根据题意可知,拼成的近似长方形的长等于圆的周长的一半;根据圆的周长公式:π×2×半径,求出半径;再根据圆的面积公式:π×半径2,代入数据,即可解答。
【详解】长方形的宽:6.28×2÷3.14÷2
=12.56÷3.14÷2
=4÷2
=2(厘米)
面积:3.14×22
=3.14×4
=12.56(平方厘米)
【点睛】本题考查圆的周长公式和面积公式的应用,关键数明确拼成的近似长方形的长等于圆的周长的一半,进而求出圆的半径。
12. 25.12 25.12
【分析】观察图形可知,阴影部分的周长等于半径为4cm圆的周长的一半加上直径为4cm圆的周长;根据圆的周长公式:π×2×半径,代入数据,求出阴影部分周长;下半部分阴影与上部分空白处相等,阴影部分面积等于半径为4cm圆的面积的一半;根据圆的面积公式:π×半径2,代入数据,即可解答。
【详解】周长:3.14×2×4÷2+3.14×4
=6.28×4÷2+12.56
=25.12÷2+12.56
=12.56+12.56
=25.12(厘米)
面积:3.14×42÷2
=3.14×16÷2
=50.24÷2
=25.12(平方厘米)
【点睛】本题考查阴影部分的的周长和面积的求法,以及圆的周长公式、面积公式的应用,关键数熟记公式。
13.1256cm2
【分析】根据圆的周长公式:周长=π×2×半径;半径=周长÷π÷2,代入数据,求出树干的半径;再根据圆的面积公式:面积=π×半径2,代入数据,即可解答。
【详解】半径:125.6÷3.14÷2
=40÷2
=20(cm)
面积:3.14×202
=3.14×400
=1256(cm2)
【点睛】本题考查圆的周长公司、面积公式的应用,关键是熟记公式,灵活运用。
14.50.24
【分析】由题意可知:圆的周长是26-0.88=25.12分米,带入圆的周长公式即可求出圆的半径,再将半径值带入圆的面积公式即可解答。
【详解】(26-0.88)÷3.14÷2
=25.12÷3.14÷2
=4(分米)
3.14×42=50.24(平方分米)
【点睛】本题主要考查圆的周长、面积公式的灵活运用,求出半径值是解题的关键。
15. 转化 50.24
【分析】在推导圆的面积公式时,把一个圆平均分成若干等份,然后再拼成一个近似的长方形,将求圆的面积转化为求长方形的面积,是运用转化思想;拼成的长方形的长是圆周长的一半,根据圆的周长公式求出圆的半径,再带入圆的面积公式计算即可。
【详解】在推导圆的面积公式时,把一个圆平均分成若干等份,然后再拼成一个近似的长方形,这是用了数学上的转化思想。
12.56×2÷3.14÷2
=25.12÷3.14÷2
=8÷2
=4(厘米)
3.14×42=50.24(平方厘米)
【点睛】明确将圆拼成近似的长方形时长方形的长是圆周长的一半是解题的关键。
16.157
【分析】由图知:阴影部分的面积是以大圆半径为直角边的三角形面积减以小圆半径为直角边的三角形面积,也就是大圆的半径平方减小圆半径的平方等于25×2=50平方厘米。又据圆环的面积=(大圆半径平方-小圆半径平方)×3.14=50×3.14,据此计算出积即求得圆环面积。
【详解】25×2=50(平方厘米)
50×3.14=157(平方厘米)
【点睛】理解大圆半径平方与小圆半径平方差是50平方厘米,带入圆环面积公式是解答此题的关键。
17.×
【分析】面积与周长的定义不同:圆的表面或围成的圆形表面的大小,叫做圆的面积;围成圆的一周的长度叫做这个圆的周长;所采用的计量单位也不同:此题中,周长的单位是厘米,面积的单位是平方厘米,单位不能统一,所以没法比较它们的大小。只能说半径是2厘米的圆的周长和面积的数据相等。
【详解】圆的周长:2×3.14×2=12.56(厘米)
圆的面积:3.14×22
=3.14×4
=12.56(平方厘米)
可见圆的周长和圆的面积虽然得出的数据一样,但计算方法不一样,单位不一样,表达的意义也不一样,所以面积和周长无法比较。
故答案为:×
【点睛】此题的解题关键是充分理解圆的面积和周长的意义。这里要注意:单位不能统一的数据无法比较它们的大小。
18.√
【分析】根据题意,可设两圆的半径分别为2,1,那么根据圆的周长公式C=2πr进行计算,然后再进行比较即可得到答案。
【详解】设两圆的半径分别为2、1,
两个圆周长的比为:
(3.14×2×2):∶(3.14×2×1)
=12.56∶6.28
=2∶1
故答案:√
【点睛】此题主要考查的是圆半径与周长的关系,解答此题关键是掌握两个圆半径的比等于两个圆的周长的比。
19.√
【分析】设圆的半径是,按周长公式,计算出现在的周长,减去以前的周长,判断答案是否正确。
【详解】
故答案为:√
【点睛】此类问题可以把圆的半径用相应的数字或字母代替,然后利用圆的周长公式表示出圆的周长进行解答。
20.×
【分析】将图形沿着一条直线对折,如果直线两侧的部分能够完全重合,折痕所在的直线叫做它的对称轴,圆的直径是一条线段不是圆的对称轴,直径所在的直线是圆的对称轴;据此解答。
【详解】圆形的对称轴:每条直径所在的直线,圆有无数条对称轴;半圆的对称轴:圆心和弧中点连线所在的直线,半圆只有1条对称轴。
故答案为:×
【点睛】掌握对称轴的意义是解答题目的关键。
21.×
【分析】圆的周长=2πr,圆的面积=πr2。根据积的变化规律,如果一个因数扩大(或缩小)若干倍,另一个因数不变,那么积也扩大(或缩小)相同倍数,则圆的半径扩大3倍,周长也扩大3倍,面积扩大3×3=9倍。
【详解】一个圆的半径扩大3倍,周长也扩大3倍,面积扩大9倍。
故答案为:×
【点睛】本题考查圆的周长、面积公式和积的变化规律的综合应用。
22.3.87平方厘米
【分析】由图可知,阴影部分的面积=长方形的面积-半圆的面积。
【详解】6×(6÷2)-×3.14×(6÷2)2
=6×3-×3.14×9
=18-1.57×9
=18-14.13
=3.87(平方厘米)
23.251.2平方厘米
【分析】阴影部分是一个圆环,圆环的面积=π(R2-r2),据此解答。
【详解】3.14×(122-82)
=3.14×(144-64)
=3.14×80
=251.2(平方厘米)
24.(1)7850平方米
(2)6分钟
【分析】(1)根据圆的面积公式:S=πr2,据此代入数值进行计算即可;
(2)根据圆的周长公式:C=πd,据此求出湖的一周的长度,再根据路程÷速度=时间,据此解答即可。
【详解】(1)3.14×(100÷2)2
=3.14×2500
=7850(平方米)
答:这个湖的水面面积是7850平方米。
(2)
=314÷52
≈6(分钟)
答:她绕湖周大约用了6分钟。
【点睛】本题考查圆的周长和面积,熟记公式是解题的关键。
25.25米
【分析】由于圆形花坛是封闭图形,则间距数=棵树,由此即可知道间距数是100,由于1个间距是1.57米,则这个圆形花坛的周长:1.57×100=157米,根据圆的周长公式:C=2πr,把数代入即可求出半径。
【详解】1.57×100=157(米)
157÷3.14÷2
=50÷2
=25(米)
答:这个圆形花坛的半径是25米。
【点睛】本题主要考查植树问题以及圆的周长公式,熟练掌握圆的周长公式并灵活运用。
26.62.8平方米
【分析】由“扩建后花坛的直径与原来直径的比是3∶2”可知:扩建后的直径是原来直径的,原来的直径已知,从而可以求出扩建后的直径,进而可以求出扩建前后花坛的面积,再求差即可。
【详解】扩建后的直径:8×=12(米)
增加的面积:3.14×(12÷2)2-3.14×(8÷2)2
=3.14×(36-16)
=3.14×20
=62.8(平方米)
答:扩建后花坛的面积增加了62.8平方米。
【点睛】解答此题的关键是利用直径比求出扩建后的直径。
27.(1)见详解
(2)9.87平方厘米
【分析】(1)由于画一个半圆,则半圆的直径最大是6厘米,由此即可画图;
(2)根据半圆的面积公式:S=πr2÷2,以及长方形的面积公式,长×宽,用长方形的面积减去半圆的面积即可求解。
【详解】(1)如图所示
(2)3.14×(6÷2)2÷2
=3.14×9÷2
=28.26÷2
=14.13(平方厘米)
4×6-14.13
=24-14.13
=9.87(平方厘米)
答:剩下部分的面积是9.87平方厘米
【点睛】本题主要考查圆的面积公式以及长方形的面积公式,熟练掌握它们的公式并灵活运用。
28.5圈
【分析】根据圆的周长=2πr,求出球的周长,用滚动距离÷周长即可。
【详解】(16.2-0.5)÷(2×3.14×0.5)
=15.7÷3.14
=5(圈)
答:需要转动5圈。
【点睛】明确滚动的总路程是(16.2-0.5)米是解决本题的关键。
答案第1页,共2页
答案第1页,共2页
