2013-2014学年度第一学期阶段学业水平检测与反馈九年级数学试题
文档属性
| 名称 | 2013-2014学年度第一学期阶段学业水平检测与反馈九年级数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 255.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-16 11:23:44 | ||
图片预览


文档简介
2013-----2014学年度第一学期阶段(二)学业水平检测与反馈
九年级数学试题 时间100分钟 满分120分
一、选择题 (本题有15个小题,每小题3分,满分45分,下面每小题给出的四个选项中,只有一个是正确的).
1.使用直角钢尺检查某一工件是否恰好是半圆形的凹面,成半圆形的为合格,如图所示的四种情况中合格的是 ( )
2 .给出下列命题:①四条边相等的四边形是正方形;②两组邻边分别相等的四边形是平行四边形;③有一个角是直角的平行四边形是矩形;④两条对角线互相垂直且平分的四边形是菱形.。其中错误命题的个数是( )
A.1 B.2 C.3 D.4
3.、用配方法解方程,下列配方正确的是 ( )
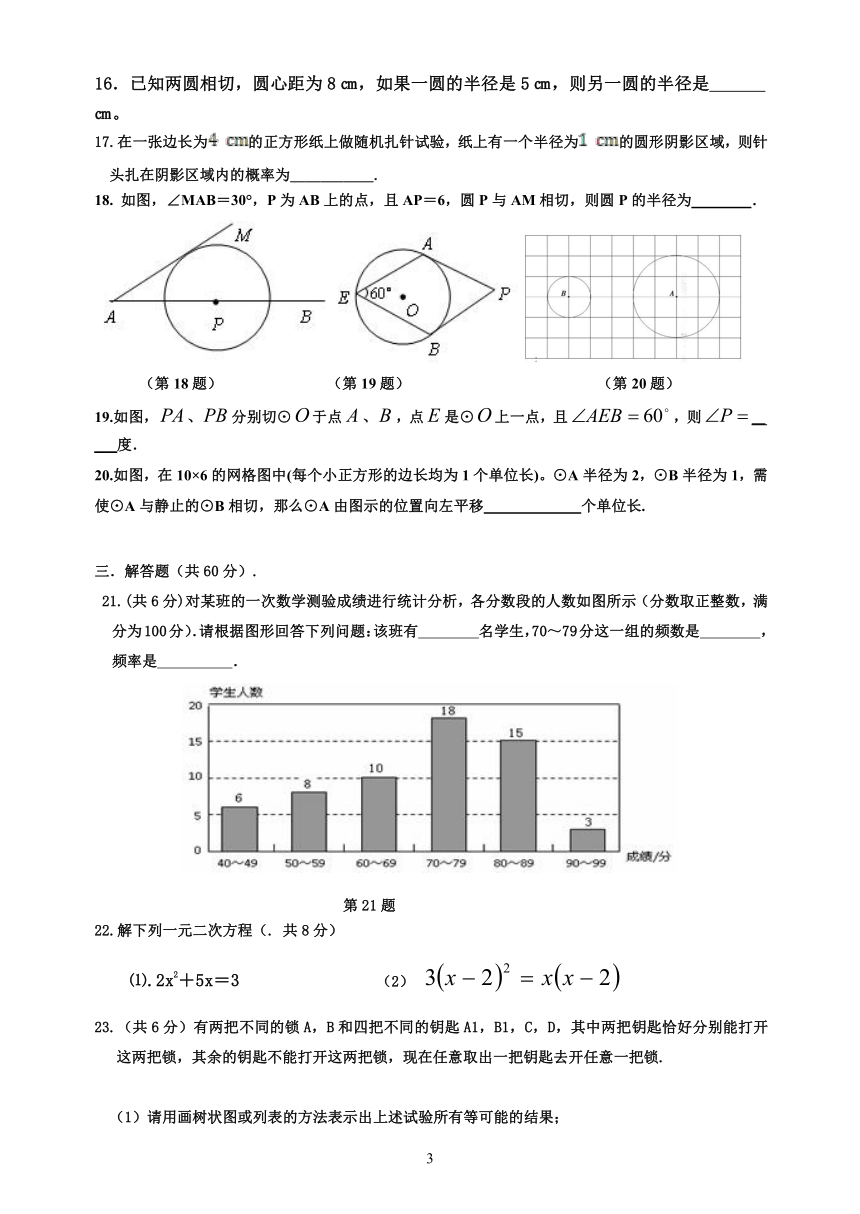
A. B. C. D.
4.已知⊙O1与⊙O2的半径分别为4和6,O1O2=2,则⊙O1与⊙O2的位置关系是 ( )
A.内切 B.相交 C.外切 D.外离
5.⊙O的直径为12㎝,弦AB垂直平分半径OC,则弦AB的长为( )
A.3㎝ B.6㎝ C.6㎝ D.12㎝
6.为了绿化校园,某校计划经过两年时间,绿地面积增加21%.设平均每年绿地面积增长率为x,则方程可列为( ).
A. (1+x)2 =21% B. (1+x) +(1+x)2 =21%
C. (1+x)2 =1+21% D. (1+x) +(1+x)2 =1+21%
7.如图,绕点逆时针旋转到的位置,已知,则等于( ).
A. B. C. D.
(第8题)
8、如图,⊙A、⊙B、⊙C、⊙D、⊙E相互外离,它们的半径都是1,顺次连结五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)的面积之和是( )
(A)π (B)1.5π (C)2π (D)2.5π
9.如图 ,□ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3 cm,则AB的长为 ( )
A.3 cm B.6 cm C.9 cm D.12 cm
10.如图,矩形ABCD沿AE折叠,使点D落在BC边上的F点处,如果∠BAF=60°,那么∠DAE等于( ).
A.15° B.30° C.45° D. 60°
(第9题) (第10题) (第11题)
11. 如图,直线AB与⊙O相切于点A,⊙O的半径为2,若∠OBA = 30°,则OB的长为( )
A. B.4 C. D.2
12. 如图,AB是⊙O的直径,点D在的延长线上,切于若则 等于( )
A. B. C. D.
(第12题) ( 第13题) (第14题)
13、如图,AB是半圆的直径,AB=2r,C、D为半圆的三等分点,则图中
阴影部分的面积是( )。
A、πr2 B、πr2 C、πr2 D、πr2
14. 如图,A、B、C、是⊙O上的三点,∠BAC=45°,则∠BOC的
大小是( )。
A.90° B.60° C.45° D.22.5°
15、、若等腰梯形两底之差等于一腰的长,那么这个梯形一内角是( )
A、 B、 C、 D、
二、填空题(本题共5个小题,每小题3分,共15分)
16.已知两圆相切,圆心距为8㎝,如果一圆的半径是5㎝,则另一圆的半径是 ㎝。
17.在一张边长为的正方形纸上做随机扎针试验,纸上有一个半径为的圆形阴影区域,则针头扎在阴影区域内的概率为___________.
18. 如图,∠MAB=30°,P为AB上的点,且AP=6,圆P与AM相切,则圆P的半径为 .
(第18题) (第19题) (第20题)
19.如图,、分别切⊙于点、,点是⊙上一点,且,则__ ___度.
20.如图,在10×6的网格图中(每个小正方形的边长均为1个单位长)。⊙A半径为2,⊙B半径为1,需使⊙A与静止的⊙B相切,那么⊙A由图示的位置向左平移 个单位长.
三.解答题(共60分).
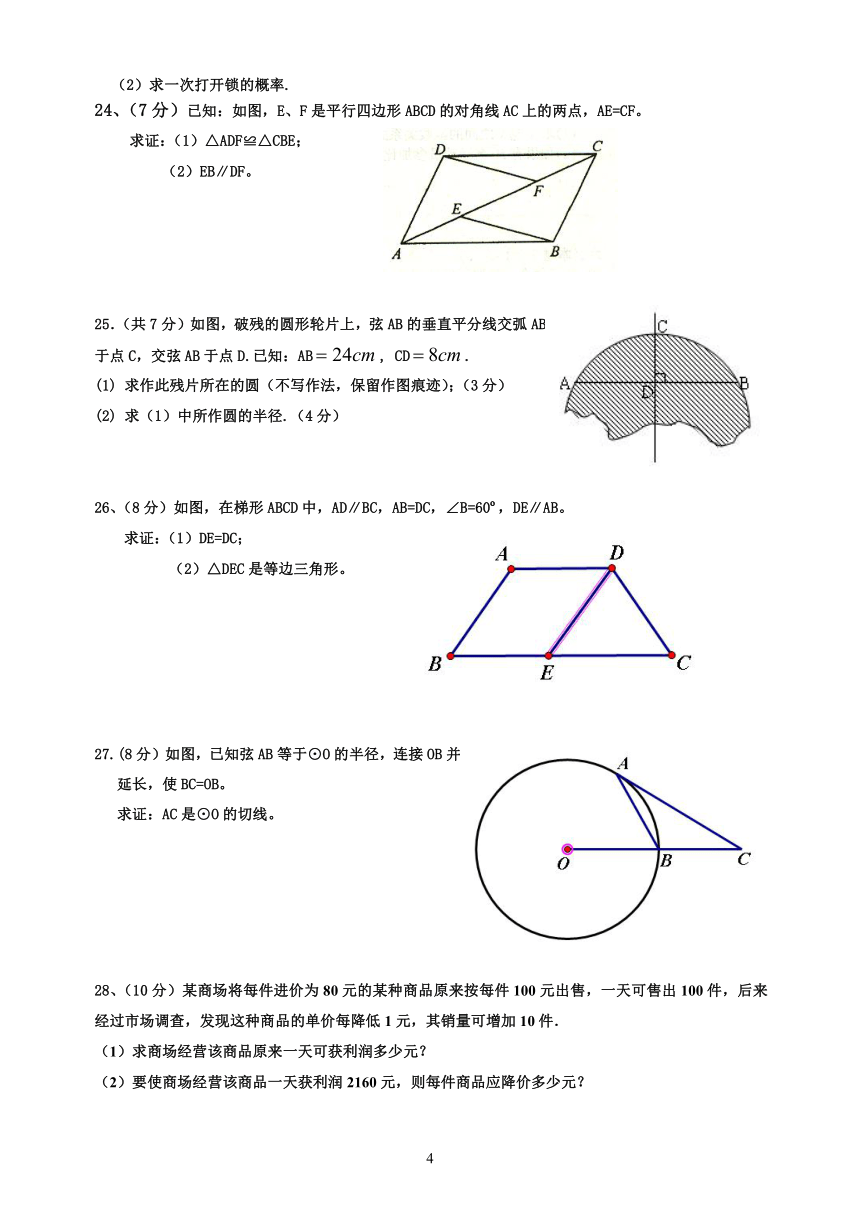
21.(共6分)对某班的一次数学测验成绩进行统计分析,各分数段的人数如图所示(分数取正整数,满分为100分).请根据图形回答下列问题:该班有 名学生,70~79分这一组的频数是 ,频率是 .
第21题
解下列一元二次方程(. 共8分)
⑴.2x2+5x=3 (2)
23.(共6分)有两把不同的锁A,B和四把不同的钥匙A1,B1,C,D,其中两把钥匙恰好分别能打开这两把锁,其余的钥匙不能打开这两把锁,现在任意取出一把钥匙去开任意一把锁.
(1)请用画树状图或列表的方法表示出上述试验所有等可能的结果;
(2)求一次打开锁的概率.
24、(7分)已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF。
求证:(1)△ADF≌△CBE;
(2)EB∥DF。
25.(共7分)如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB, CD.
求作此残片所在的圆(不写作法,保留作图痕迹);(3分)
求(1)中所作圆的半径.(4分)
26、(8分)如图,在梯形ABCD中,AD∥BC,AB=DC,∠B=60 ,DE∥AB。
求证:(1)DE=DC;
(2)△DEC是等边三角形。
27.(8分)如图,已知弦AB等于⊙O的半径,连接OB并延长,使BC=OB。
求证:AC是⊙O的切线。
28、(10分)某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件,后来经过市场调查,发现这种商品的单价每降低1元,其销量可增加10件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)要使商场经营该商品一天获利润2160元,则每件商品应降价多少元?
2013-----2014学年度第一学期阶段(二)学业水平检测与反馈
九年级数学答案卷
一.选择题(共45分)。
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
答案
二.填空题(共15分)。
16__________ . 17_________ . 18___________. 19___________.20________
三.解答题(共60分)
21.(共6分.
(1)________________ (2)_________________ (3)_________________
22.解下列一元二次方程(. 共8分)
⑴.2x2+5x=3 (2)
23.(共6分)
⑴
(2)
24、(7分)
⑴
(2)
25.(共7分)
⑴
(2)
26、(8分)
(1)
(2)
27.(8分)
28、(10分)
(1)
(2)
(第7题)
班级___________ 姓名_________ 考号_____
PAGE
1
九年级数学试题 时间100分钟 满分120分
一、选择题 (本题有15个小题,每小题3分,满分45分,下面每小题给出的四个选项中,只有一个是正确的).
1.使用直角钢尺检查某一工件是否恰好是半圆形的凹面,成半圆形的为合格,如图所示的四种情况中合格的是 ( )
2 .给出下列命题:①四条边相等的四边形是正方形;②两组邻边分别相等的四边形是平行四边形;③有一个角是直角的平行四边形是矩形;④两条对角线互相垂直且平分的四边形是菱形.。其中错误命题的个数是( )
A.1 B.2 C.3 D.4
3.、用配方法解方程,下列配方正确的是 ( )
A. B. C. D.
4.已知⊙O1与⊙O2的半径分别为4和6,O1O2=2,则⊙O1与⊙O2的位置关系是 ( )
A.内切 B.相交 C.外切 D.外离
5.⊙O的直径为12㎝,弦AB垂直平分半径OC,则弦AB的长为( )
A.3㎝ B.6㎝ C.6㎝ D.12㎝
6.为了绿化校园,某校计划经过两年时间,绿地面积增加21%.设平均每年绿地面积增长率为x,则方程可列为( ).
A. (1+x)2 =21% B. (1+x) +(1+x)2 =21%
C. (1+x)2 =1+21% D. (1+x) +(1+x)2 =1+21%
7.如图,绕点逆时针旋转到的位置,已知,则等于( ).
A. B. C. D.
(第8题)
8、如图,⊙A、⊙B、⊙C、⊙D、⊙E相互外离,它们的半径都是1,顺次连结五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)的面积之和是( )
(A)π (B)1.5π (C)2π (D)2.5π
9.如图 ,□ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3 cm,则AB的长为 ( )
A.3 cm B.6 cm C.9 cm D.12 cm
10.如图,矩形ABCD沿AE折叠,使点D落在BC边上的F点处,如果∠BAF=60°,那么∠DAE等于( ).
A.15° B.30° C.45° D. 60°
(第9题) (第10题) (第11题)
11. 如图,直线AB与⊙O相切于点A,⊙O的半径为2,若∠OBA = 30°,则OB的长为( )
A. B.4 C. D.2
12. 如图,AB是⊙O的直径,点D在的延长线上,切于若则 等于( )
A. B. C. D.
(第12题) ( 第13题) (第14题)
13、如图,AB是半圆的直径,AB=2r,C、D为半圆的三等分点,则图中
阴影部分的面积是( )。
A、πr2 B、πr2 C、πr2 D、πr2
14. 如图,A、B、C、是⊙O上的三点,∠BAC=45°,则∠BOC的
大小是( )。
A.90° B.60° C.45° D.22.5°
15、、若等腰梯形两底之差等于一腰的长,那么这个梯形一内角是( )
A、 B、 C、 D、
二、填空题(本题共5个小题,每小题3分,共15分)
16.已知两圆相切,圆心距为8㎝,如果一圆的半径是5㎝,则另一圆的半径是 ㎝。
17.在一张边长为的正方形纸上做随机扎针试验,纸上有一个半径为的圆形阴影区域,则针头扎在阴影区域内的概率为___________.
18. 如图,∠MAB=30°,P为AB上的点,且AP=6,圆P与AM相切,则圆P的半径为 .
(第18题) (第19题) (第20题)
19.如图,、分别切⊙于点、,点是⊙上一点,且,则__ ___度.
20.如图,在10×6的网格图中(每个小正方形的边长均为1个单位长)。⊙A半径为2,⊙B半径为1,需使⊙A与静止的⊙B相切,那么⊙A由图示的位置向左平移 个单位长.
三.解答题(共60分).
21.(共6分)对某班的一次数学测验成绩进行统计分析,各分数段的人数如图所示(分数取正整数,满分为100分).请根据图形回答下列问题:该班有 名学生,70~79分这一组的频数是 ,频率是 .
第21题
解下列一元二次方程(. 共8分)
⑴.2x2+5x=3 (2)
23.(共6分)有两把不同的锁A,B和四把不同的钥匙A1,B1,C,D,其中两把钥匙恰好分别能打开这两把锁,其余的钥匙不能打开这两把锁,现在任意取出一把钥匙去开任意一把锁.
(1)请用画树状图或列表的方法表示出上述试验所有等可能的结果;
(2)求一次打开锁的概率.
24、(7分)已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF。
求证:(1)△ADF≌△CBE;
(2)EB∥DF。
25.(共7分)如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB, CD.
求作此残片所在的圆(不写作法,保留作图痕迹);(3分)
求(1)中所作圆的半径.(4分)
26、(8分)如图,在梯形ABCD中,AD∥BC,AB=DC,∠B=60 ,DE∥AB。
求证:(1)DE=DC;
(2)△DEC是等边三角形。
27.(8分)如图,已知弦AB等于⊙O的半径,连接OB并延长,使BC=OB。
求证:AC是⊙O的切线。
28、(10分)某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件,后来经过市场调查,发现这种商品的单价每降低1元,其销量可增加10件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)要使商场经营该商品一天获利润2160元,则每件商品应降价多少元?
2013-----2014学年度第一学期阶段(二)学业水平检测与反馈
九年级数学答案卷
一.选择题(共45分)。
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
答案
二.填空题(共15分)。
16__________ . 17_________ . 18___________. 19___________.20________
三.解答题(共60分)
21.(共6分.
(1)________________ (2)_________________ (3)_________________
22.解下列一元二次方程(. 共8分)
⑴.2x2+5x=3 (2)
23.(共6分)
⑴
(2)
24、(7分)
⑴
(2)
25.(共7分)
⑴
(2)
26、(8分)
(1)
(2)
27.(8分)
28、(10分)
(1)
(2)
(第7题)
班级___________ 姓名_________ 考号_____
PAGE
1
同课章节目录
