青岛版数学七年级下册 综合与实践 多边形的密铺 课件(共33张PPT)
文档属性
| 名称 | 青岛版数学七年级下册 综合与实践 多边形的密铺 课件(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 00:00:00 | ||
图片预览






文档简介
(共33张PPT)
综合与实践
多边形的密铺
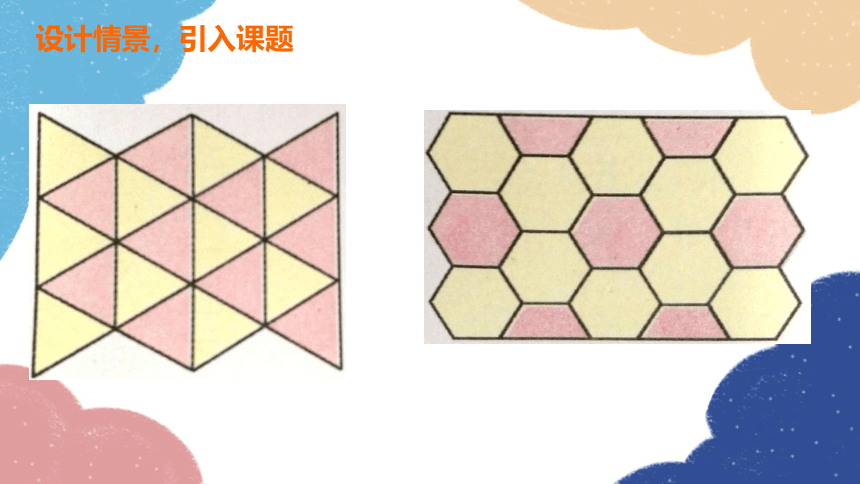
设计情景,引入课题
设计情景,引入课题
设计情景,引入课题
思考与发现
思考:
通过观察上面的图片,你发现它们有哪些共同特征?
发现:
(1)不重叠 (2)不留空隙
概念:由若干个多边形既无空隙、又不重叠地拼接,将
平面完全覆盖,称为多边形的密铺。
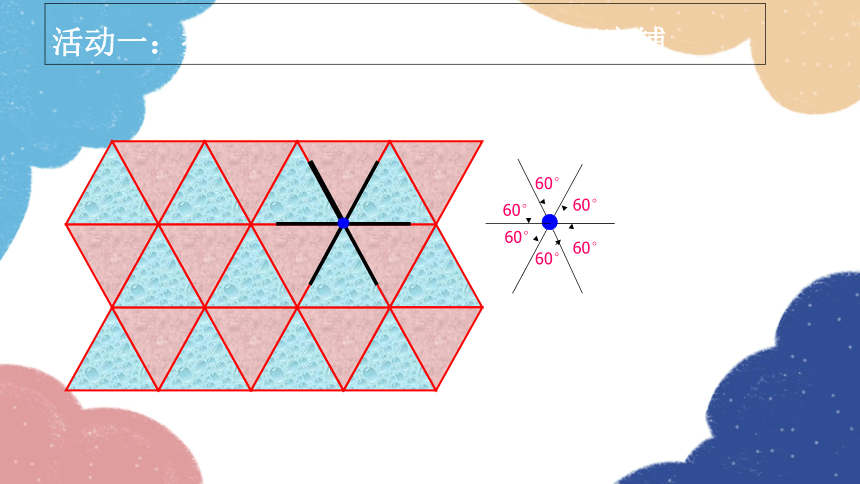
活动一:探索只用同一种正多边形进行密铺
请同学们拿出准备好的正多边形纸片,以小组为单位完成下列问题,并填好实验报告单。
1.用同一种正多边形(如正三角形、正四边形、正五边 形、正六边形)能否密铺成平面图案?
2.如果能,哪几种正多边形能密铺成平面图案? 3.能够用同一种正多边形密铺的条件是什么?
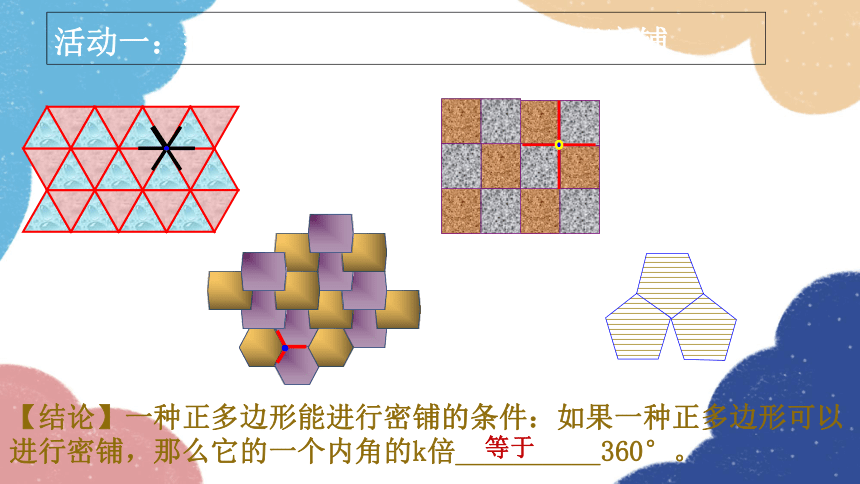
【结论】一种正多边形能进行密铺的条件:如果一种正多边形可以进行密铺,那么它的一个内角的k倍__________360°。
活动一:探索只用同一种正多边形进行密铺
60°
60°
60°
60°
60°
60°
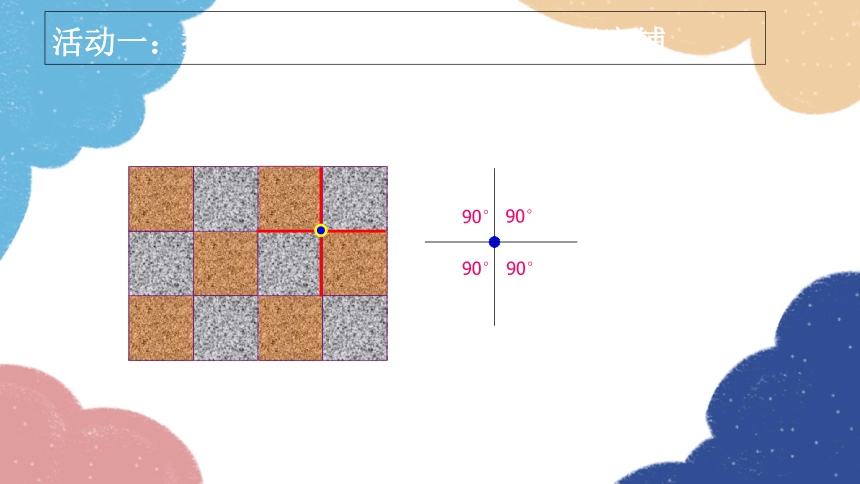
活动一:探索只用同一种正多边形进行密铺
90°
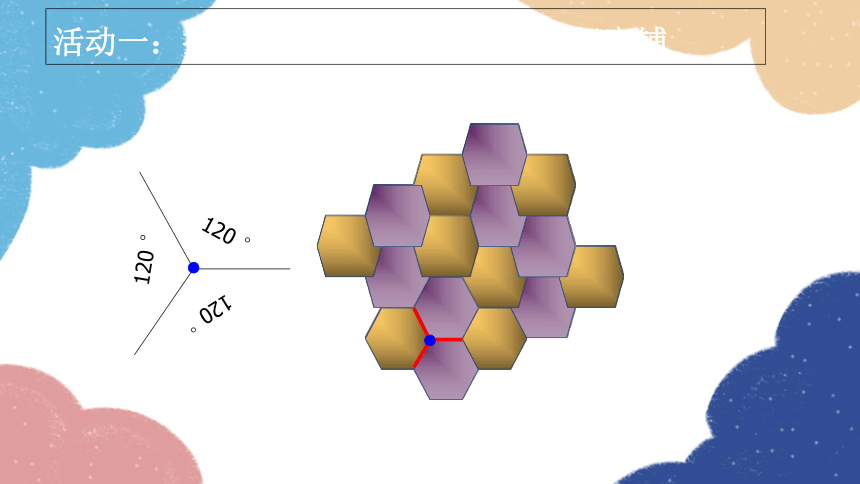
活动一:探索只用同一种正多边形进行密铺
90°
90°
90°
120 °
120 °
120 °
活动一:探索只用同一种正多边形进行密铺
108°
108°
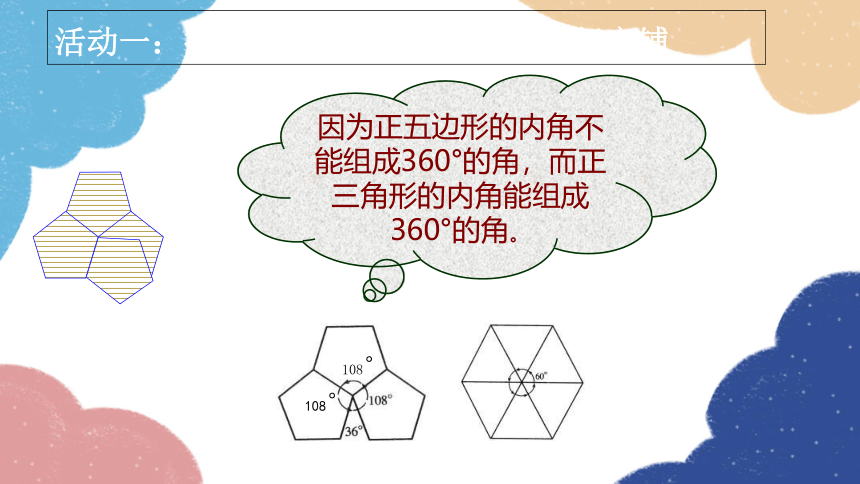
因为正五边形的内角不能组成360°的角,而正三角形的内角能组成360°的角。
活动一:探索只用同一种正多边形进行密铺
【结论】一种正多边形能进行密铺的条件:如果一种正多边形可以进行密铺,那么它的一个内角的k倍__________360°。
活动一:探索只用同一种正多边形进行密铺
等于
又n≥3,且n为正整数。
∴n-2为4的约数
∴n-2=________
∴n=___________
活动一:探索只用同一种正多边形进行密铺
1或2或4
3或4或6
思考:除了上述三种正多边形外,还有没有其他的正多边形,只用同样大小的这种正多边形就可以进行密铺?
解:设正多边形的边数为n,在拼接点处有K个角,则有:
活动二:探索用两种正多边形进行密铺
1.用正三角形与正方形结合拼图,能否密铺成平面图案?请你试一试,并填好实验报告单。
2.还能用其他的两种正多边形进行密铺吗?
活动二:探索用两种正多边形进行密铺
【结论】如果用两种正多边形进行密铺,在拼接点处的各内角的度数和一定等于 。两种正多边形的边长_ _。
活动二:探索用两种正多边形进行密铺
1.正三角形与正六边形的密铺(图案1)
60°
60°
120°
60°
60°
每个顶点处正六边形1个,正三角形4个.
活动二:探索用两种正多边形进行密铺
2.正三角形与正六边形的密铺(图案2)
120°
120°
60°
60°
【结论】如果用两种正多边形进行密铺,在拼接点处的各内角的度数和一定等于_________。两种正多边形的边长_________。
活动二:探索用两种正多边形进行密铺
360°
相等
思考:用几个正三角形与正六边形可以密铺?
解:设一个顶点周围有m个正三角形、n个正六边形,则有方程:
__________+__________=360°
∴ m+2n=6,又m、n为正整数,解得m=2,n=2,或者m=4,n=1。
即用两个正三角形和两个正六边形或者用四个正三角形和一个正六边形可以密铺。
活动二:探索用两种正多边形进行密铺
n×120°
m×60°
活动二:探索用两种正多边形进行密铺
延伸:用正四边形与正八边形能否密铺?若能,则在一个顶点处有_____个正方形_____个正八边形。
1
2
活动三:探究任意三角形与任意四边形的密铺。
问题: 1.形状大小完全相同的任意三角形能密铺成平面图形吗? 2.形状大小完全相同的任意四边形能密铺成平面图形吗?
分小组试一试,并完成实验报告单。
活动三:探究任意三角形与任意四边形的密铺。
【结论】任意三角形、任意四边形_______________________密铺。
活动三:探究任意三角形与任意四边形的密铺。
结论:
形状、大小完全相同的任意
三角形能密铺成平面图形。
结论:
形状、大小相同的任意四边形能密铺成平面图形
归纳小结,交流感悟
谈一谈本课的学习有哪些收获和体会?
1.平面密铺:无空隙,不重复。
2.多边形平面密铺的条件:
顶点公用,边长相等。
一个顶点处各内角之和为360°。
3.两种正多边形密铺的条件:
两种正多边形的各内角的整数倍之和为360°。
两种正多边形的边长相等。
密铺图片欣赏
密铺图片欣赏
密铺图片欣赏
密铺图片欣赏
密铺图片欣赏
荷兰画家埃舍尔创作了许多用单一的精美图形铺满平面的图案奇作,作品中的具象图形不论是鱼、神兽,还是骑士,都是那么严谨、生动,真可谓鬼斧神工,妙手天成。
共同探讨,设计图案
要求:
1.如果用正多边形密铺,设计时必须用两种(或两种以上)正 多边形密铺。 2.也可以用不规则的图形,设计丰富多彩的密铺图案。
课后延伸,弘扬个性
1.课下设计用三种正多边形进行密铺的图案(可以用彩色拼,也可以自己画或者在电脑上操作)比一比,看谁设计的更漂亮!
2.你能围绕多边形的密铺问题作进一步的探讨吗?就你研究的过程与结果写成一篇小论文,在班内交流。
综合与实践
多边形的密铺
设计情景,引入课题
设计情景,引入课题
设计情景,引入课题
思考与发现
思考:
通过观察上面的图片,你发现它们有哪些共同特征?
发现:
(1)不重叠 (2)不留空隙
概念:由若干个多边形既无空隙、又不重叠地拼接,将
平面完全覆盖,称为多边形的密铺。
活动一:探索只用同一种正多边形进行密铺
请同学们拿出准备好的正多边形纸片,以小组为单位完成下列问题,并填好实验报告单。
1.用同一种正多边形(如正三角形、正四边形、正五边 形、正六边形)能否密铺成平面图案?
2.如果能,哪几种正多边形能密铺成平面图案? 3.能够用同一种正多边形密铺的条件是什么?
【结论】一种正多边形能进行密铺的条件:如果一种正多边形可以进行密铺,那么它的一个内角的k倍__________360°。
活动一:探索只用同一种正多边形进行密铺
60°
60°
60°
60°
60°
60°
活动一:探索只用同一种正多边形进行密铺
90°
活动一:探索只用同一种正多边形进行密铺
90°
90°
90°
120 °
120 °
120 °
活动一:探索只用同一种正多边形进行密铺
108°
108°
因为正五边形的内角不能组成360°的角,而正三角形的内角能组成360°的角。
活动一:探索只用同一种正多边形进行密铺
【结论】一种正多边形能进行密铺的条件:如果一种正多边形可以进行密铺,那么它的一个内角的k倍__________360°。
活动一:探索只用同一种正多边形进行密铺
等于
又n≥3,且n为正整数。
∴n-2为4的约数
∴n-2=________
∴n=___________
活动一:探索只用同一种正多边形进行密铺
1或2或4
3或4或6
思考:除了上述三种正多边形外,还有没有其他的正多边形,只用同样大小的这种正多边形就可以进行密铺?
解:设正多边形的边数为n,在拼接点处有K个角,则有:
活动二:探索用两种正多边形进行密铺
1.用正三角形与正方形结合拼图,能否密铺成平面图案?请你试一试,并填好实验报告单。
2.还能用其他的两种正多边形进行密铺吗?
活动二:探索用两种正多边形进行密铺
【结论】如果用两种正多边形进行密铺,在拼接点处的各内角的度数和一定等于 。两种正多边形的边长_ _。
活动二:探索用两种正多边形进行密铺
1.正三角形与正六边形的密铺(图案1)
60°
60°
120°
60°
60°
每个顶点处正六边形1个,正三角形4个.
活动二:探索用两种正多边形进行密铺
2.正三角形与正六边形的密铺(图案2)
120°
120°
60°
60°
【结论】如果用两种正多边形进行密铺,在拼接点处的各内角的度数和一定等于_________。两种正多边形的边长_________。
活动二:探索用两种正多边形进行密铺
360°
相等
思考:用几个正三角形与正六边形可以密铺?
解:设一个顶点周围有m个正三角形、n个正六边形,则有方程:
__________+__________=360°
∴ m+2n=6,又m、n为正整数,解得m=2,n=2,或者m=4,n=1。
即用两个正三角形和两个正六边形或者用四个正三角形和一个正六边形可以密铺。
活动二:探索用两种正多边形进行密铺
n×120°
m×60°
活动二:探索用两种正多边形进行密铺
延伸:用正四边形与正八边形能否密铺?若能,则在一个顶点处有_____个正方形_____个正八边形。
1
2
活动三:探究任意三角形与任意四边形的密铺。
问题: 1.形状大小完全相同的任意三角形能密铺成平面图形吗? 2.形状大小完全相同的任意四边形能密铺成平面图形吗?
分小组试一试,并完成实验报告单。
活动三:探究任意三角形与任意四边形的密铺。
【结论】任意三角形、任意四边形_______________________密铺。
活动三:探究任意三角形与任意四边形的密铺。
结论:
形状、大小完全相同的任意
三角形能密铺成平面图形。
结论:
形状、大小相同的任意四边形能密铺成平面图形
归纳小结,交流感悟
谈一谈本课的学习有哪些收获和体会?
1.平面密铺:无空隙,不重复。
2.多边形平面密铺的条件:
顶点公用,边长相等。
一个顶点处各内角之和为360°。
3.两种正多边形密铺的条件:
两种正多边形的各内角的整数倍之和为360°。
两种正多边形的边长相等。
密铺图片欣赏
密铺图片欣赏
密铺图片欣赏
密铺图片欣赏
密铺图片欣赏
荷兰画家埃舍尔创作了许多用单一的精美图形铺满平面的图案奇作,作品中的具象图形不论是鱼、神兽,还是骑士,都是那么严谨、生动,真可谓鬼斧神工,妙手天成。
共同探讨,设计图案
要求:
1.如果用正多边形密铺,设计时必须用两种(或两种以上)正 多边形密铺。 2.也可以用不规则的图形,设计丰富多彩的密铺图案。
课后延伸,弘扬个性
1.课下设计用三种正多边形进行密铺的图案(可以用彩色拼,也可以自己画或者在电脑上操作)比一比,看谁设计的更漂亮!
2.你能围绕多边形的密铺问题作进一步的探讨吗?就你研究的过程与结果写成一篇小论文,在班内交流。
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
