人教版九年级数学上册23.1图形的旋转 导学案及作业设计(无答案)
文档属性
| 名称 | 人教版九年级数学上册23.1图形的旋转 导学案及作业设计(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 237.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 15:46:02 | ||
图片预览

文档简介
人教版九年级数学上册第二十三章
《图形的旋转》学习任务单及作业设计
第一课时
【学习目标】
1.通过观察具体实例认识旋转,归纳旋转的概念.
2.探索旋转的性质,会按要求画简单平面图形旋转后的图形.
【课前学习任务】
复习平移、轴对称的定义和性质,以及发现性质的过程与方法.
【课上学习任务】
学习任务一:
想一想:
时钟的指针在不停地转动,从 3 时到 5 时,时针是如何转动的?
_________________________________________________________________
学习任务二:
探究:
1.线段 OA 与 OA′有什么关系?
2.∠AOA′与∠BOB′有什么关系?
3.△ABC 与△A′B′C′的形状和大小有什么关系?
学习任务三:
任意画一个△ABC,作下列旋转:
1.以点 A 为中心,把△ABC 逆时针旋转 40°;
2.在△ABC 外任取一点为中心,把△ABC顺时针旋转90°;
3.以 AC 的中点为中心,把△ABC 旋转180°.
学习任务四:
△A′B′C′是由△ABC 旋转得到的,你能找出旋转中心点 O 吗?(要求尺规作图)
【作业设计】
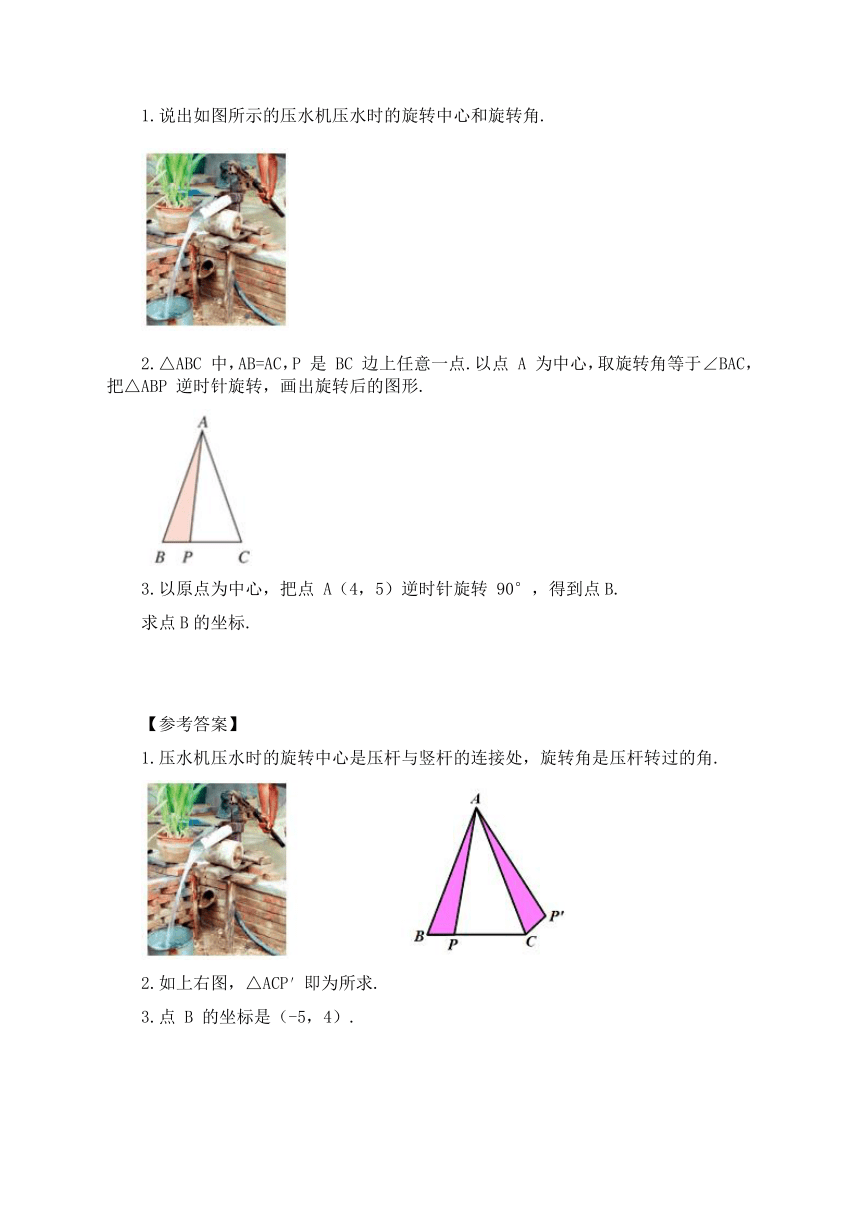
1.说出如图所示的压水机压水时的旋转中心和旋转角.
2.△ABC 中,AB=AC,P 是 BC 边上任意一点.以点 A 为中心,取旋转角等于∠BAC,把△ABP 逆时针旋转,画出旋转后的图形.
3.以原点为中心,把点 A(4,5)逆时针旋转 90°,得到点B.
求点B的坐标.
【参考答案】
1.压水机压水时的旋转中心是压杆与竖杆的连接处,旋转角是压杆转过的角.
2.如上右图,△ACP′即为所求.
3.点 B 的坐标是(-5,4).
第二课时
【学习目标】
1.通过对比平移、轴对称、旋转的相同点和不同点,进一步形成图形变换的知识体系.
2.运用多种方法解决问题,认识画旋转后图形的本质.
3.了解旋转对称的概念及其在生活中的应用.
【课前学习任务】
复习旋转的定义及其性质,复习画旋转后图形的方法.
【课上学习任务】
学习任务一:
对比平移、轴对称、旋转的相同点和不同点,完成表格.
平移 轴对称 旋转
相同点
不同点 定义
图形
要素
性质
学习任务二:
例:如图,E是正方形 ABCD 中CD边上一点,以点A为中心,把△ADE顺时针旋转90°.
(1)画出旋转后的图形;
(2)若 AD=4,DE=3,点E旋转后的对应点为E′,求EE′的长.
学习任务三:
观察图片,体会把一个图案进行旋转,选择不同的旋转中心,不同点的旋转角,出现不同的效果. 理解旋转对称的概念及其在生活中的应用.
【作业设计】
1.把图中的五角星图案,绕着它的中心O旋转. 旋转角至少为多少度时,旋转后的五角星能与自身重合?对等边三角形进行类似的讨论.
2.如图,△ABC 中,∠C=90°.
(1)将△ABC 绕点B逆时针旋转90°,画出旋转后的三角形;
(2)若 BC=3,AC=4,点A旋转后的对应点为A′,求A′A的长.
3.如图,△ABD,△AEC 都是等边三角形. BE 与 DC 有什么关系?你能用旋转的性质说明上述关系成立的理由吗?
【参考答案】
1.五角星图案,绕着点O旋转,旋转角至少为72°时,旋转后的五角星能和自身重合. 等边三角形绕着中心旋转,旋转角为120°或120°的整数倍时,旋转后的等边三角形能和自身重合.
2.(1)△A′BC′即为所求.
(2)∵ △ABC中,∠C=90°,BC=3,AC=4.
∴ AB=5. 由旋转的性质可得
△A′BA中,∠A′BA = 90°,A′B=AB=5.
∴ AA′= .
3. ∵ △AEC是等边三角形,
∴ AE=AC,∠EAC=60°.
同理,AB=AD,∠BAD=60°.
∴ 以点A为旋转中心将△EAB 顺时针旋转60°就得到△CAD.
∴ △EAB≌△CAD,
∴ BE=DC .
《图形的旋转》学习任务单及作业设计
第一课时
【学习目标】
1.通过观察具体实例认识旋转,归纳旋转的概念.
2.探索旋转的性质,会按要求画简单平面图形旋转后的图形.
【课前学习任务】
复习平移、轴对称的定义和性质,以及发现性质的过程与方法.
【课上学习任务】
学习任务一:
想一想:
时钟的指针在不停地转动,从 3 时到 5 时,时针是如何转动的?
_________________________________________________________________
学习任务二:
探究:
1.线段 OA 与 OA′有什么关系?
2.∠AOA′与∠BOB′有什么关系?
3.△ABC 与△A′B′C′的形状和大小有什么关系?
学习任务三:
任意画一个△ABC,作下列旋转:
1.以点 A 为中心,把△ABC 逆时针旋转 40°;
2.在△ABC 外任取一点为中心,把△ABC顺时针旋转90°;
3.以 AC 的中点为中心,把△ABC 旋转180°.
学习任务四:
△A′B′C′是由△ABC 旋转得到的,你能找出旋转中心点 O 吗?(要求尺规作图)
【作业设计】
1.说出如图所示的压水机压水时的旋转中心和旋转角.
2.△ABC 中,AB=AC,P 是 BC 边上任意一点.以点 A 为中心,取旋转角等于∠BAC,把△ABP 逆时针旋转,画出旋转后的图形.
3.以原点为中心,把点 A(4,5)逆时针旋转 90°,得到点B.
求点B的坐标.
【参考答案】
1.压水机压水时的旋转中心是压杆与竖杆的连接处,旋转角是压杆转过的角.
2.如上右图,△ACP′即为所求.
3.点 B 的坐标是(-5,4).
第二课时
【学习目标】
1.通过对比平移、轴对称、旋转的相同点和不同点,进一步形成图形变换的知识体系.
2.运用多种方法解决问题,认识画旋转后图形的本质.
3.了解旋转对称的概念及其在生活中的应用.
【课前学习任务】
复习旋转的定义及其性质,复习画旋转后图形的方法.
【课上学习任务】
学习任务一:
对比平移、轴对称、旋转的相同点和不同点,完成表格.
平移 轴对称 旋转
相同点
不同点 定义
图形
要素
性质
学习任务二:
例:如图,E是正方形 ABCD 中CD边上一点,以点A为中心,把△ADE顺时针旋转90°.
(1)画出旋转后的图形;
(2)若 AD=4,DE=3,点E旋转后的对应点为E′,求EE′的长.
学习任务三:
观察图片,体会把一个图案进行旋转,选择不同的旋转中心,不同点的旋转角,出现不同的效果. 理解旋转对称的概念及其在生活中的应用.
【作业设计】
1.把图中的五角星图案,绕着它的中心O旋转. 旋转角至少为多少度时,旋转后的五角星能与自身重合?对等边三角形进行类似的讨论.
2.如图,△ABC 中,∠C=90°.
(1)将△ABC 绕点B逆时针旋转90°,画出旋转后的三角形;
(2)若 BC=3,AC=4,点A旋转后的对应点为A′,求A′A的长.
3.如图,△ABD,△AEC 都是等边三角形. BE 与 DC 有什么关系?你能用旋转的性质说明上述关系成立的理由吗?
【参考答案】
1.五角星图案,绕着点O旋转,旋转角至少为72°时,旋转后的五角星能和自身重合. 等边三角形绕着中心旋转,旋转角为120°或120°的整数倍时,旋转后的等边三角形能和自身重合.
2.(1)△A′BC′即为所求.
(2)∵ △ABC中,∠C=90°,BC=3,AC=4.
∴ AB=5. 由旋转的性质可得
△A′BA中,∠A′BA = 90°,A′B=AB=5.
∴ AA′= .
3. ∵ △AEC是等边三角形,
∴ AE=AC,∠EAC=60°.
同理,AB=AD,∠BAD=60°.
∴ 以点A为旋转中心将△EAB 顺时针旋转60°就得到△CAD.
∴ △EAB≌△CAD,
∴ BE=DC .
同课章节目录
