人教A版(2019)高中数学必修第二册 《平面向量基本定理》名师课件(共38张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 《平面向量基本定理》名师课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 18:13:55 | ||
图片预览



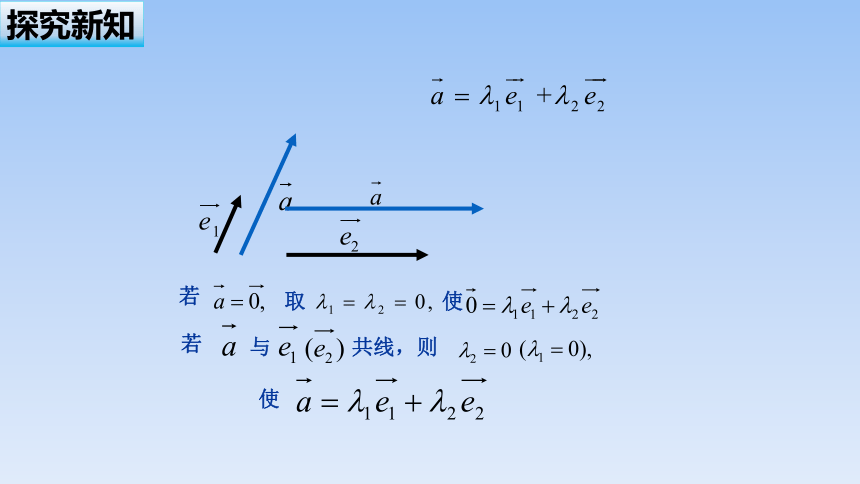



文档简介
(共38张PPT)
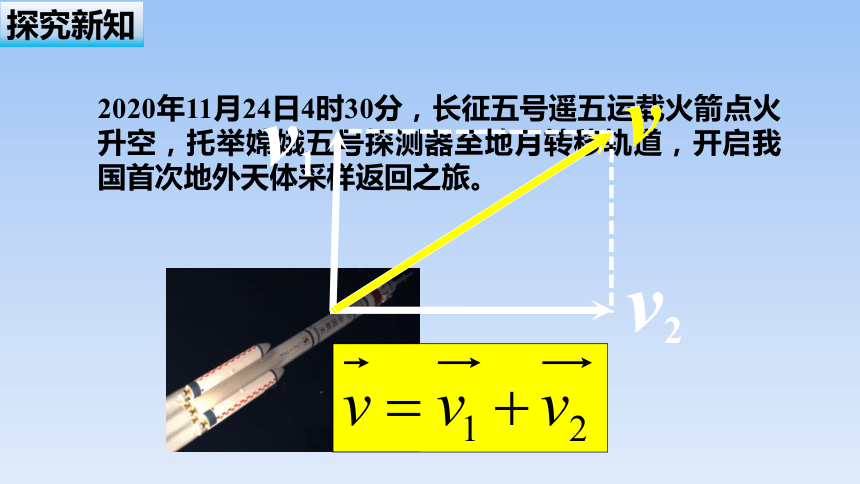
(1)小明从A到B,再从B到C,则他两次的位移之和是:
A
B
C
D
(2)向量共线定理:
三角形法则
平行四边形法则
首尾相接,由首至尾
共起点
反之,如果是共线向量,那么有且只有一个实数
复习引入
人教A版同步教材名师课件
平面向量基本定理
学习目标
学 习 目 标 核心素养
了解向量基底的含义,在平面内,当一个基底选定后,会用这个基底表示其他向量. 数学抽象
会用平面向量基本定理解决相关问题. 逻辑推理
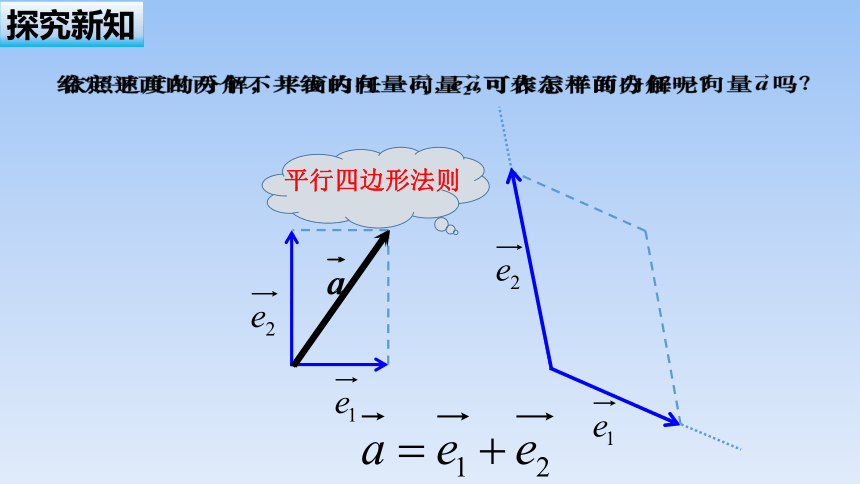
2020年11月24日4时30分,长征五号遥五运载火箭点火升空,托举嫦娥五号探测器至地月转移轨道,开启我国首次地外天体采样返回之旅。
v
v1
v2
v
探究新知
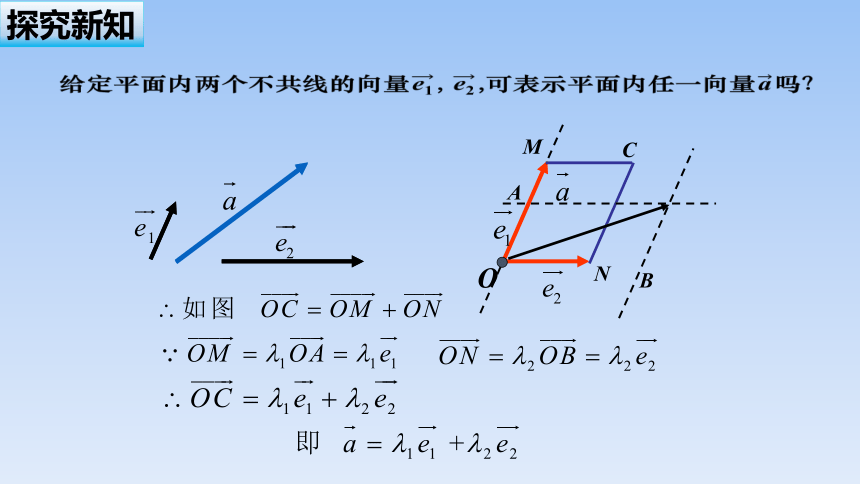
依照速度的分解,平面内任一向量可作怎样的分解呢?
平行四边形法则
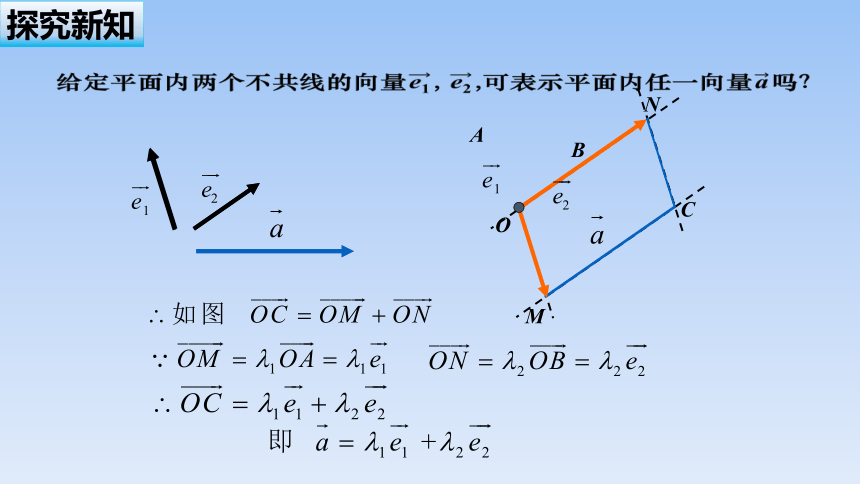
给定平面内两个不共线的向量, ,可表示平面内任一向量吗?
探究新知
O
C
A
B
M
N
探究新知
给定平面内两个不共线的向量, ,可表示平面内任一向量吗?
O
C
A
B
M
N
探究新知
给定平面内两个不共线的向量, ,可表示平面内任一向量吗?
取
使
若
与
共线,则
使
若
探究新知
(1)平面向量基本定理
存 在 性
唯 一 性
存在
如果
是同一平面内两个不共线向量,
那么对于这一平面的任意向量
一对实数,
使
有且只有
思考:
上述表达式中的
是否唯一?
( 2 )
基底:
把不共线的向量
叫做这一平面内
所有向量的一组基底.
探究新知
(1)一个平面内,可作为基底的向量有 对。
无数
①③
探究新知
(2)设O是 两对角线的交点,已知下列向量组:
①与;② 与;③ 与;④ 与,其中可作为这个平行四边形所在平面的基底的有:
唯一
0
内的任何向量都可以用这组基底来表
中的实数对
是______确定的。
(4)若向量
不共线,且
如果
,那么
(3)选定基底后,这个平面
示,并且
(5)若
是一组基底,若
,则
_____
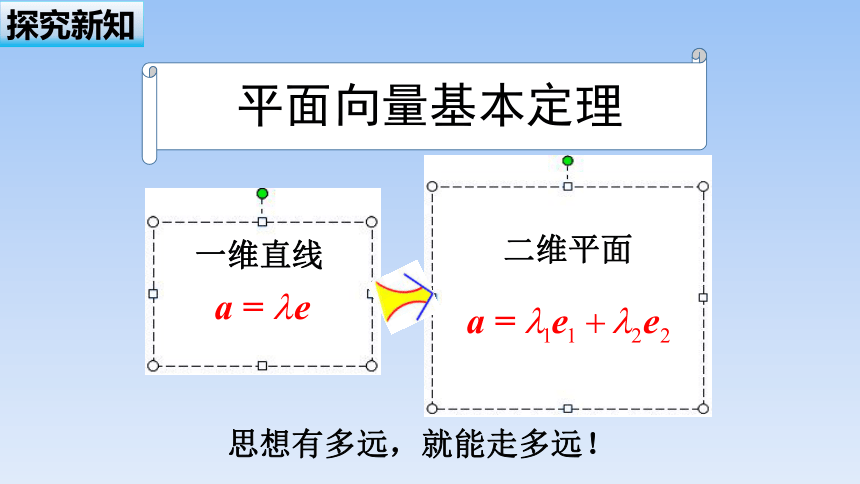
探究新知
一维直线
平面向量基本定理
二维平面
思想有多远,就能走多远!
探究新知
例1、设O是平行四边形ABCD两对角线的交点,给出下列向量组:
①与;② 与;③ 与;④ 与,其中可作为这个平行四边形所在平面的一组基底的是( )
A.①② B.①③ C.①④ D.③④
① 与不共线;②=-,则与共线;③与不共线;④ =- ,则与共线.由平面向量基底的概念知,只有不共线的两个向量才能构成一组基底,故①③满足题意.
B
典例讲解
解析
对基底的理解
(1)两个向量能否作为一组基底,关键是看这两个向量是否共线.若共线,则不能作基底,反之,则可作基底.
(2)一个平面的基底若确定,那么平面上任意一个向量都可以由这组基底唯一线性表示出来,设向量与是平面内两个不共线的向量,若x1+y1=x2+y2,则
方法归纳
1、若向量不共线,则=,=,试判断能否作为基底.
设存在实数λ,使=λ,则=λ(),
即(2-3λ)+(2λ-1)=0,
由于向量不共线,
所以2-3λ=2λ-1=0,这样的λ是不存在的,
从而不共线能作为基底.
解:
变式训练
例2、如图所示,在 ABCD中,点E,F分别为BC,DC边上的中点,DE与BF交于点G,若=, =,试用表示向量, .
=++
=-++
=-++=-
=++
=-++=-
变式训练
条件不变,试用基底表示.
由平面几何知识知BG=BF,故=+= + =+()=+-=+.
若=, =,试用表示向量, .
= + =2+ =-2+ =-2+
= + =2+ =-2+ =-2+
典例讲解
解析
(1)运用向量的线性运算法则对待求向量不断进行转化,直至用基底表示为止.
(2)通过列向量方程或方程组的形式,利用基底表示向量的唯一性求解.
用基底表示向量的两种方法
方法归纳
2、如图,在平行四边形ABCD中,M,N分别为DC,BC的中点,已知=, =,试用表示和.
设=, =,则由M,N分别为DC,BC的中点,可得=, =.
在△ABN与△ADM中,可得
用向量表示,
得
故 =.
变式训练
解析
例3、已知||=||,且与的夹角为120°,求+与的夹角及-与的夹角.
如图,作=, =,∠AOB=120°,以,为邻边作平行四边形OACB,则=+, =-.
典例讲解
因为||=|| ,所以平行四边形OACB为菱形.
所以与的夹角∠AOC=60°,
与的夹角即为与的夹角∠ABC=30°.
所以+与的夹角为60°, -与的夹角为30°.
解析
(1)实质:两个向量的夹角,实质上是从同一起点出发的两个非零向量构成的角.
(2)关键:求两个向量的夹角,关键是利用平移的方法使两个向量的起点重合,然后按照“一作二证三算”的步骤,并结合平面几何知识求出两个向量的夹角.
两个向量夹角的实质及求解的关键
方法归纳
3、如图,已知△ABC是等边三角形.
(1)求向量与向量的夹角;
(2)若E为BC的中点,求向量与向量的夹角.
(1)因为△ABC为等边三角形,所以∠ABC=60°.
如图,延长AB至点D,使AB=BD,则= ,
(2)因为E为BC的中点,所以AE⊥BC,
所以向量与向量的夹角为90°.
所以∠DBC为向量与向量的夹角.
因为∠DBC=120°,所以向量与向量的夹角为120°.
变式训练
解析
典例讲解
例4、如图,在△ABC中, ,P是BN上的一点,若,则实数m的值为(
解析
又
思路分析 利用己得,利用点B,P,N共线的条件得出的值.
C
方法归纳
包含两层意思:
( 1)当点P在直线AB上时满足该式;
(2)当点Р满足该式时,点P一定在直线AB上.
变式训练
4. 如图,一直线EF与平行四边形ABCD的两边AB,AD分别交于点E,F,且交其对角线AC于点K,若,则的值为_______.
解析
又E,F,K三点共线,
典例讲解
例5、如图所示, 是两个不共线的非零向量,N为线段OB的中点,M为线段OA上靠近点A 的三等分点,点C在直线MN上,且 , 的最小值为(
解析
因为点C,M ,N三点共线,所以存在实数 , ,使 ,且又,所以 1,故, 1.易知当取得最小值,最小值为
A
变式训练
5. 如图所示,A,B,C是圆О上的三点,线段CO的延长线与BA 的延长线交于圆О外的一点D,若,则 + 的取值范围是_______.
解析
由题意得,
,
, ,
, 的取值范围为(-1,0).
(-1,0)
典例讲解
例6、已知是平面内所有向量的一个基底,且,若,试求、的值.
思路分析 先用基底表示,再将所得的表达式与条件加以对照,可得有关、 的方程组,解方程组即可求得、 的值.
解析
由题意可得
,且是平面内所有向量的一个基底,
解得
方法归纳
利用平面向量基本定理求参数的题型的常见形式:
一个向量用基底表示,求相应系数的值.对于这类题型,一般先利用向量的运算法则将该向量用同一个基底表示出来,再与已知中给出的形式对照,利用基底表示向量的唯一性求出参数的值.
变式训练
6.设D,E分别是△ABC的边AB,BC上的点, .若(, 为实数),则+ =
解析
,且与不共线, ,
故
典例讲解
例7、如图,在平行四边形ABCD中,F是边CD的中点,AF与BD交于点E,用向量方法证明:E为线段BD的三等分点.
解析
设,则
因为点A,E,F与点B,D,E分别共线,所以存在实数, ,使 , ,
于是 , - ,所以因为与不共线,所以,解得,
所以,所以点E为线段BD(靠近D)的三等分点.
典例讲解
例8、如图所示,在△ABC中,AD为BC边上的中线,E在边AC上且AE= 2EC,BE交AD于点G,求及的值.
解析
设, =u. AD为BC边上的中线,
,
又,
又 不共线
变式训练
7.如图,在平行四边形ABCD中,M、N分别是边DC、BC的中点.
解析
(1)求证:
(2)设,且,求实数, 的值.
(1) M、N分别是边DC、BC的中点,
,
且
(2),
,
.
1.基底的性质
(1)不共线性:平面内两个不共线的向量才可以作为一组基底,基底不同,表示也不同.由于零向量与任何向量共线,所以零向量不可以作为基底.
(2)不唯一性:对基底的选取不唯一,平面内任一向量a都可被这个平面的一组基底e1,e2线性表示,且在基底确定后,这样的表示是唯一的.
2.两个向量的夹角
(1)向量的夹角是针对非零向量定义的.
(2)向量的夹角和直线的夹角范围是不同的,它们的范围分别是[0,π]和[0,].
素养提炼
当堂练习
1.已知平行四边形ABCD,则下列各组向量中可以作为该平面内所有向量的一个基底的是( )
D
2.设D为△ABC 所在平面内一点,若,则( )
A
当堂练习
3.已知{, }是表示平面内所有向量的一个基底,那么下面四组向量中不能作为一个基底的是( )
A
4.( )
1
B
5.
.
3
1、平面向量基本定理、两向量的夹角
2、对基本定理的理解
(1)基底不唯一,关键是不共线
(2)实数对 的存在性和唯一性
二、思想方法总结:待定系数法、数形结合、转化思想、方程思想、类比归纳
一、知识总结
归纳小结
归纳小结
平面向量基本定理
基本定理内容
基底
应用
不共线向量,
(,不共线)
作 业
课本27页 练习1、2、 3
(1)小明从A到B,再从B到C,则他两次的位移之和是:
A
B
C
D
(2)向量共线定理:
三角形法则
平行四边形法则
首尾相接,由首至尾
共起点
反之,如果是共线向量,那么有且只有一个实数
复习引入
人教A版同步教材名师课件
平面向量基本定理
学习目标
学 习 目 标 核心素养
了解向量基底的含义,在平面内,当一个基底选定后,会用这个基底表示其他向量. 数学抽象
会用平面向量基本定理解决相关问题. 逻辑推理
2020年11月24日4时30分,长征五号遥五运载火箭点火升空,托举嫦娥五号探测器至地月转移轨道,开启我国首次地外天体采样返回之旅。
v
v1
v2
v
探究新知
依照速度的分解,平面内任一向量可作怎样的分解呢?
平行四边形法则
给定平面内两个不共线的向量, ,可表示平面内任一向量吗?
探究新知
O
C
A
B
M
N
探究新知
给定平面内两个不共线的向量, ,可表示平面内任一向量吗?
O
C
A
B
M
N
探究新知
给定平面内两个不共线的向量, ,可表示平面内任一向量吗?
取
使
若
与
共线,则
使
若
探究新知
(1)平面向量基本定理
存 在 性
唯 一 性
存在
如果
是同一平面内两个不共线向量,
那么对于这一平面的任意向量
一对实数,
使
有且只有
思考:
上述表达式中的
是否唯一?
( 2 )
基底:
把不共线的向量
叫做这一平面内
所有向量的一组基底.
探究新知
(1)一个平面内,可作为基底的向量有 对。
无数
①③
探究新知
(2)设O是 两对角线的交点,已知下列向量组:
①与;② 与;③ 与;④ 与,其中可作为这个平行四边形所在平面的基底的有:
唯一
0
内的任何向量都可以用这组基底来表
中的实数对
是______确定的。
(4)若向量
不共线,且
如果
,那么
(3)选定基底后,这个平面
示,并且
(5)若
是一组基底,若
,则
_____
探究新知
一维直线
平面向量基本定理
二维平面
思想有多远,就能走多远!
探究新知
例1、设O是平行四边形ABCD两对角线的交点,给出下列向量组:
①与;② 与;③ 与;④ 与,其中可作为这个平行四边形所在平面的一组基底的是( )
A.①② B.①③ C.①④ D.③④
① 与不共线;②=-,则与共线;③与不共线;④ =- ,则与共线.由平面向量基底的概念知,只有不共线的两个向量才能构成一组基底,故①③满足题意.
B
典例讲解
解析
对基底的理解
(1)两个向量能否作为一组基底,关键是看这两个向量是否共线.若共线,则不能作基底,反之,则可作基底.
(2)一个平面的基底若确定,那么平面上任意一个向量都可以由这组基底唯一线性表示出来,设向量与是平面内两个不共线的向量,若x1+y1=x2+y2,则
方法归纳
1、若向量不共线,则=,=,试判断能否作为基底.
设存在实数λ,使=λ,则=λ(),
即(2-3λ)+(2λ-1)=0,
由于向量不共线,
所以2-3λ=2λ-1=0,这样的λ是不存在的,
从而不共线能作为基底.
解:
变式训练
例2、如图所示,在 ABCD中,点E,F分别为BC,DC边上的中点,DE与BF交于点G,若=, =,试用表示向量, .
=++
=-++
=-++=-
=++
=-++=-
变式训练
条件不变,试用基底表示.
由平面几何知识知BG=BF,故=+= + =+()=+-=+.
若=, =,试用表示向量, .
= + =2+ =-2+ =-2+
= + =2+ =-2+ =-2+
典例讲解
解析
(1)运用向量的线性运算法则对待求向量不断进行转化,直至用基底表示为止.
(2)通过列向量方程或方程组的形式,利用基底表示向量的唯一性求解.
用基底表示向量的两种方法
方法归纳
2、如图,在平行四边形ABCD中,M,N分别为DC,BC的中点,已知=, =,试用表示和.
设=, =,则由M,N分别为DC,BC的中点,可得=, =.
在△ABN与△ADM中,可得
用向量表示,
得
故 =.
变式训练
解析
例3、已知||=||,且与的夹角为120°,求+与的夹角及-与的夹角.
如图,作=, =,∠AOB=120°,以,为邻边作平行四边形OACB,则=+, =-.
典例讲解
因为||=|| ,所以平行四边形OACB为菱形.
所以与的夹角∠AOC=60°,
与的夹角即为与的夹角∠ABC=30°.
所以+与的夹角为60°, -与的夹角为30°.
解析
(1)实质:两个向量的夹角,实质上是从同一起点出发的两个非零向量构成的角.
(2)关键:求两个向量的夹角,关键是利用平移的方法使两个向量的起点重合,然后按照“一作二证三算”的步骤,并结合平面几何知识求出两个向量的夹角.
两个向量夹角的实质及求解的关键
方法归纳
3、如图,已知△ABC是等边三角形.
(1)求向量与向量的夹角;
(2)若E为BC的中点,求向量与向量的夹角.
(1)因为△ABC为等边三角形,所以∠ABC=60°.
如图,延长AB至点D,使AB=BD,则= ,
(2)因为E为BC的中点,所以AE⊥BC,
所以向量与向量的夹角为90°.
所以∠DBC为向量与向量的夹角.
因为∠DBC=120°,所以向量与向量的夹角为120°.
变式训练
解析
典例讲解
例4、如图,在△ABC中, ,P是BN上的一点,若,则实数m的值为(
解析
又
思路分析 利用己得,利用点B,P,N共线的条件得出的值.
C
方法归纳
包含两层意思:
( 1)当点P在直线AB上时满足该式;
(2)当点Р满足该式时,点P一定在直线AB上.
变式训练
4. 如图,一直线EF与平行四边形ABCD的两边AB,AD分别交于点E,F,且交其对角线AC于点K,若,则的值为_______.
解析
又E,F,K三点共线,
典例讲解
例5、如图所示, 是两个不共线的非零向量,N为线段OB的中点,M为线段OA上靠近点A 的三等分点,点C在直线MN上,且 , 的最小值为(
解析
因为点C,M ,N三点共线,所以存在实数 , ,使 ,且又,所以 1,故, 1.易知当取得最小值,最小值为
A
变式训练
5. 如图所示,A,B,C是圆О上的三点,线段CO的延长线与BA 的延长线交于圆О外的一点D,若,则 + 的取值范围是_______.
解析
由题意得,
,
, ,
, 的取值范围为(-1,0).
(-1,0)
典例讲解
例6、已知是平面内所有向量的一个基底,且,若,试求、的值.
思路分析 先用基底表示,再将所得的表达式与条件加以对照,可得有关、 的方程组,解方程组即可求得、 的值.
解析
由题意可得
,且是平面内所有向量的一个基底,
解得
方法归纳
利用平面向量基本定理求参数的题型的常见形式:
一个向量用基底表示,求相应系数的值.对于这类题型,一般先利用向量的运算法则将该向量用同一个基底表示出来,再与已知中给出的形式对照,利用基底表示向量的唯一性求出参数的值.
变式训练
6.设D,E分别是△ABC的边AB,BC上的点, .若(, 为实数),则+ =
解析
,且与不共线, ,
故
典例讲解
例7、如图,在平行四边形ABCD中,F是边CD的中点,AF与BD交于点E,用向量方法证明:E为线段BD的三等分点.
解析
设,则
因为点A,E,F与点B,D,E分别共线,所以存在实数, ,使 , ,
于是 , - ,所以因为与不共线,所以,解得,
所以,所以点E为线段BD(靠近D)的三等分点.
典例讲解
例8、如图所示,在△ABC中,AD为BC边上的中线,E在边AC上且AE= 2EC,BE交AD于点G,求及的值.
解析
设, =u. AD为BC边上的中线,
,
又,
又 不共线
变式训练
7.如图,在平行四边形ABCD中,M、N分别是边DC、BC的中点.
解析
(1)求证:
(2)设,且,求实数, 的值.
(1) M、N分别是边DC、BC的中点,
,
且
(2),
,
.
1.基底的性质
(1)不共线性:平面内两个不共线的向量才可以作为一组基底,基底不同,表示也不同.由于零向量与任何向量共线,所以零向量不可以作为基底.
(2)不唯一性:对基底的选取不唯一,平面内任一向量a都可被这个平面的一组基底e1,e2线性表示,且在基底确定后,这样的表示是唯一的.
2.两个向量的夹角
(1)向量的夹角是针对非零向量定义的.
(2)向量的夹角和直线的夹角范围是不同的,它们的范围分别是[0,π]和[0,].
素养提炼
当堂练习
1.已知平行四边形ABCD,则下列各组向量中可以作为该平面内所有向量的一个基底的是( )
D
2.设D为△ABC 所在平面内一点,若,则( )
A
当堂练习
3.已知{, }是表示平面内所有向量的一个基底,那么下面四组向量中不能作为一个基底的是( )
A
4.( )
1
B
5.
.
3
1、平面向量基本定理、两向量的夹角
2、对基本定理的理解
(1)基底不唯一,关键是不共线
(2)实数对 的存在性和唯一性
二、思想方法总结:待定系数法、数形结合、转化思想、方程思想、类比归纳
一、知识总结
归纳小结
归纳小结
平面向量基本定理
基本定理内容
基底
应用
不共线向量,
(,不共线)
作 业
课本27页 练习1、2、 3
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
