人教A版(2019)高中数学必修第二册 《平面向量数乘运算的坐标表示》名师课件(共42张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 《平面向量数乘运算的坐标表示》名师课件(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 00:00:00 | ||
图片预览





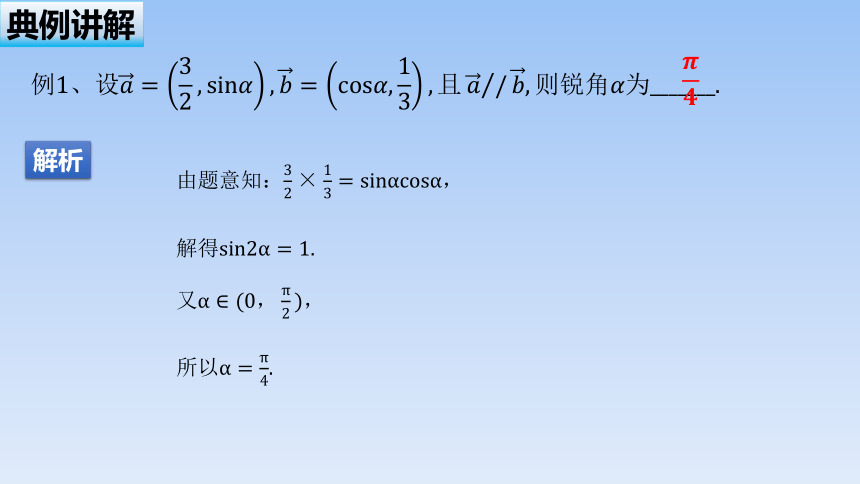





文档简介
(共42张PPT)
1.向量共线定理:
2.平面向量的坐标运算:
注:向量坐标等于终点坐标减去起点坐标
复习引入
人教A版同步教材名师课件
平面向量数乘运算的坐标表示
x
y
O
P1
P2
P
课程目标 学科素养
A.掌握向量数乘运算的坐标表示; B.会根据向量的坐标,判断向量是否共线. 1.数学抽象:向量数乘运算的坐标表示;
2.逻辑推理:推导共线向量的坐标表示;
3.数学运算:由向量共线求参数的值;
4.直观想象:学会用坐标进行向量的相关运算,理解数学内容之间的内在联系;
5.数学模型:通过对共线向量坐标关系的探究,提高分析问题、解决问题的能力。
学习目标
探究新知
已知,能够快速求出的坐标吗?
即
实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标.
思考一
思考二
探究新知
向量共线定理的坐标形式
如果用坐标表示,可写为
思考:两个向量共线的条件是什么?如何用坐标表示两个共线向量?
探究新知
典例讲解
由题意知:,
解得.
又
所以.
解析
∵
例2、已知当为何值时, 平行时它们是同向还是反向
解析
法一:当 时,存在唯一实数入 ,使,
即,得解得,
即当 时, ,此时,
典例讲解
∵.
法二:由题意得,,解得:.
此时.
当时, ,且方向相反.
例2、已知当为何值时, 平行时它们是同向还是反向
解析
典例讲解
方法归纳
向量共线的判定方法
①利用向量共线定理,由推出.
②利用向量共线的坐标公式直接求解.
变式训练
1. 已知A(2,1),B(0,4),C(1,3),D(5,-3), 与是否共线 如果共线,它们的方向相同还是相反
解析
共线且方向相反.
变式训练
2.已知A,B,C三点的坐标分别为(-1,0),(3,-1),(1,2),并且,求证:.
解析
设依题意有
, ,
, , .
, ,
.又 , .
典例讲解
例3、在△AOB中,已知点O(0,0) ,A(0,5),B(4,3) , 与交于点 ,求点的坐标.
解析
,
,则 三点共线,
易知
三点共线, ,
由①②解得
方法归纳
①寻找共线向量
②利用已知点的坐标求出共线向量的坐标
③设出待求点的坐标,用含的式子表示含有的向量的坐标
④利用共线向量的坐标表示列方程(组)
⑤解方程(组)求出点的坐标
对于利用向量共线的坐标表示求点的坐标的问题,还可以利用向量共线定理求解.
利用向量共线的坐标表示求点的坐标的步骤
变式训练
3.平面上有A(-2,1),B(1,4),D(4,-3)三点,点C在直线AB上,且,连接 DC,点E在CD上,且,求E点的坐标.
解析
.
设点坐标为,则
, , ,
.设点坐标为() ,则
.
典例讲解
例4、设点若向量与共线且同向,则的值为( )
A.2 B.-2 C. D.1
解析
由已知条件得,显然.由与共线得,解得 .
当时, ,则有,满足与同向;当时, , ,则有,此时与反向,不符合题意.
因此,符合条件的只有
A
典例讲解
例5、已知向量是不共线的两个向量且,求的值.
,
∴存在实数,使得
即.
∴ ,解得:.
解析
由向量共线求参数值的方法
方法归纳
变式训练
4.已知向量,则的值等于( )
A. B. C. D.2
解析
.
A
变式训练
5.已知,则 .
解析
变式训练
6.平面内给定三个向量
( 1 )求满足的实数的值;
( 2 )若,求实数的值.
解析
,
,,
.
A
B
C
典例讲解
例6、已知试判断三点之间的位置关系.
在直角坐标系中作出三点,观察图形,猜想三点共线。
证明如下
∵
∴ .
∵直线、直线有公共点,
∴ 三点共线.
解析
典例讲解
例7、设向量当为何值时,三点共线?
由题意知:
又三点共线.
∴
得.
∴当时,三点共线.
解析
判断向量(或三点)共线的三个步骤
方法归纳
7.如图,在直角梯形中, ,过作E,M 为CE的中点,用向量法证明:
( 1 ) DE//BC;
( 2 )D,M,B三点共线.
变式训练
解析
以为原点,所在直线为轴,所在直线为轴,建立平面直角坐标系,如图,令. 四边形为正方形.各点坐标分别为
( 1 ) ,
,.
7.如图,在直角梯形中, ,过作, 为的中点,用向量法证明:
( 1 ) DE//BC;
( 2 )D,M,B三点共线.
变式训练
解析
以为原点,所在直线为轴,所在直线为轴,建立平面直角坐标系,如图,令. 四边形为正方形.各点坐标分别为
( 2 ) 为的中点,,, ,.
又与有公共点
典例讲解
例8、已知在直角坐标系平面上的四点
证明:四边形为梯形.
由题意
∴.
又,∴四边形为梯形.
证明
典例讲解
例9、已知
解析
;
不能.理由:由题意知
若四边形OABP为平行四边形,则,
典例讲解
例10、设 约定两个向量之间的运算.若,则= .
解析
设
方法归纳
在引入向量的坐标表示以后,将几何图形放到适当的平面直角坐标系中,可以把几何图形的性质转化为向量运算,这样就能进行相应的代数运算,变抽象逻辑推理为具体的向量运算,实现了“数”与“形”的有机结合,使向量运算完全代数化.这种解题方法具有普遍性,应牢固掌握.
8. 若向量,则点能否构成三角形 若能,求出实数满足的条件;若不能,请说明理由.
变式训练
解析
若点能构成三角形,则这三点不共线,由题可得
,则,解得.
所以当时,点能构成三角形.
9. 设,规定向量之间的一个运算
,已知=(1,2) ,=(-4,-3) ,则= ( )
A.(2,1) B.(-2,1) C.(2,-1) D.(-2,-1)
变式训练
解析
设,则
.
B
例11、设点P是线段P1P2上的一点,P1、P2的坐标分别是
。
(1)当点P是线段P1P2的中点时,求点P的坐标;
(2)当点P是线段P1P2的一个三等分点时,求点P的坐标。
x
y
O
P1(x1,y1)
P2(x2,y2)
P
(1)
M
中点坐标公式:
)
2
,
2
(
2
1
2
1
y
y
x
x
+
+
典例讲解
x
y
O
P1
P2
P
x
y
O
P1
P2
P
例11、设点P是线段P1P2上的一点,P1、P2的坐标分别是
。
(1)当点P是线段P1P2的中点时,求点P的坐标;
(2)当点P是线段P1P2的一个三等分点时,求点P的坐标。
典例讲解
解:
x
y
O
P1
P2
P
拓 展
你能根据前面的结论推导三角形的重心坐标公式吗?
A
B
C
E
F
D
G
则点G的坐标为
的三个顶点的坐标分别为
点G为重心,
拓 展
典例讲解
例12、已知点点在圆上运动,
求的重心的轨迹方程.
设的重心为则
解得: (1)
又因点在圆上运动,所以
将(1)式代入(2)式得:
所以的重心的轨迹方程为.
解析
素养提炼
素养提炼
当堂练习
1.已知则 =( )
A.(3,0) B.(2,1) C.(3,3) D.(3,3)
2.若三点,则B,则 ( )
A. 1 B. 3 C. D. 51
D
B
3.已知,且// , 等于 ( )
A.(5, 10) B.(4, 8) C.(3, 6) D.(2, 4)
4.已知点,若,则 点P的坐标是__________.
B
归纳小结
作 业
课本35页 练习:1、2、3、5
1.向量共线定理:
2.平面向量的坐标运算:
注:向量坐标等于终点坐标减去起点坐标
复习引入
人教A版同步教材名师课件
平面向量数乘运算的坐标表示
x
y
O
P1
P2
P
课程目标 学科素养
A.掌握向量数乘运算的坐标表示; B.会根据向量的坐标,判断向量是否共线. 1.数学抽象:向量数乘运算的坐标表示;
2.逻辑推理:推导共线向量的坐标表示;
3.数学运算:由向量共线求参数的值;
4.直观想象:学会用坐标进行向量的相关运算,理解数学内容之间的内在联系;
5.数学模型:通过对共线向量坐标关系的探究,提高分析问题、解决问题的能力。
学习目标
探究新知
已知,能够快速求出的坐标吗?
即
实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标.
思考一
思考二
探究新知
向量共线定理的坐标形式
如果用坐标表示,可写为
思考:两个向量共线的条件是什么?如何用坐标表示两个共线向量?
探究新知
典例讲解
由题意知:,
解得.
又
所以.
解析
∵
例2、已知当为何值时, 平行时它们是同向还是反向
解析
法一:当 时,存在唯一实数入 ,使,
即,得解得,
即当 时, ,此时,
典例讲解
∵.
法二:由题意得,,解得:.
此时.
当时, ,且方向相反.
例2、已知当为何值时, 平行时它们是同向还是反向
解析
典例讲解
方法归纳
向量共线的判定方法
①利用向量共线定理,由推出.
②利用向量共线的坐标公式直接求解.
变式训练
1. 已知A(2,1),B(0,4),C(1,3),D(5,-3), 与是否共线 如果共线,它们的方向相同还是相反
解析
共线且方向相反.
变式训练
2.已知A,B,C三点的坐标分别为(-1,0),(3,-1),(1,2),并且,求证:.
解析
设依题意有
, ,
, , .
, ,
.又 , .
典例讲解
例3、在△AOB中,已知点O(0,0) ,A(0,5),B(4,3) , 与交于点 ,求点的坐标.
解析
,
,则 三点共线,
易知
三点共线, ,
由①②解得
方法归纳
①寻找共线向量
②利用已知点的坐标求出共线向量的坐标
③设出待求点的坐标,用含的式子表示含有的向量的坐标
④利用共线向量的坐标表示列方程(组)
⑤解方程(组)求出点的坐标
对于利用向量共线的坐标表示求点的坐标的问题,还可以利用向量共线定理求解.
利用向量共线的坐标表示求点的坐标的步骤
变式训练
3.平面上有A(-2,1),B(1,4),D(4,-3)三点,点C在直线AB上,且,连接 DC,点E在CD上,且,求E点的坐标.
解析
.
设点坐标为,则
, , ,
.设点坐标为() ,则
.
典例讲解
例4、设点若向量与共线且同向,则的值为( )
A.2 B.-2 C. D.1
解析
由已知条件得,显然.由与共线得,解得 .
当时, ,则有,满足与同向;当时, , ,则有,此时与反向,不符合题意.
因此,符合条件的只有
A
典例讲解
例5、已知向量是不共线的两个向量且,求的值.
,
∴存在实数,使得
即.
∴ ,解得:.
解析
由向量共线求参数值的方法
方法归纳
变式训练
4.已知向量,则的值等于( )
A. B. C. D.2
解析
.
A
变式训练
5.已知,则 .
解析
变式训练
6.平面内给定三个向量
( 1 )求满足的实数的值;
( 2 )若,求实数的值.
解析
,
,,
.
A
B
C
典例讲解
例6、已知试判断三点之间的位置关系.
在直角坐标系中作出三点,观察图形,猜想三点共线。
证明如下
∵
∴ .
∵直线、直线有公共点,
∴ 三点共线.
解析
典例讲解
例7、设向量当为何值时,三点共线?
由题意知:
又三点共线.
∴
得.
∴当时,三点共线.
解析
判断向量(或三点)共线的三个步骤
方法归纳
7.如图,在直角梯形中, ,过作E,M 为CE的中点,用向量法证明:
( 1 ) DE//BC;
( 2 )D,M,B三点共线.
变式训练
解析
以为原点,所在直线为轴,所在直线为轴,建立平面直角坐标系,如图,令. 四边形为正方形.各点坐标分别为
( 1 ) ,
,.
7.如图,在直角梯形中, ,过作, 为的中点,用向量法证明:
( 1 ) DE//BC;
( 2 )D,M,B三点共线.
变式训练
解析
以为原点,所在直线为轴,所在直线为轴,建立平面直角坐标系,如图,令. 四边形为正方形.各点坐标分别为
( 2 ) 为的中点,,, ,.
又与有公共点
典例讲解
例8、已知在直角坐标系平面上的四点
证明:四边形为梯形.
由题意
∴.
又,∴四边形为梯形.
证明
典例讲解
例9、已知
解析
;
不能.理由:由题意知
若四边形OABP为平行四边形,则,
典例讲解
例10、设 约定两个向量之间的运算.若,则= .
解析
设
方法归纳
在引入向量的坐标表示以后,将几何图形放到适当的平面直角坐标系中,可以把几何图形的性质转化为向量运算,这样就能进行相应的代数运算,变抽象逻辑推理为具体的向量运算,实现了“数”与“形”的有机结合,使向量运算完全代数化.这种解题方法具有普遍性,应牢固掌握.
8. 若向量,则点能否构成三角形 若能,求出实数满足的条件;若不能,请说明理由.
变式训练
解析
若点能构成三角形,则这三点不共线,由题可得
,则,解得.
所以当时,点能构成三角形.
9. 设,规定向量之间的一个运算
,已知=(1,2) ,=(-4,-3) ,则= ( )
A.(2,1) B.(-2,1) C.(2,-1) D.(-2,-1)
变式训练
解析
设,则
.
B
例11、设点P是线段P1P2上的一点,P1、P2的坐标分别是
。
(1)当点P是线段P1P2的中点时,求点P的坐标;
(2)当点P是线段P1P2的一个三等分点时,求点P的坐标。
x
y
O
P1(x1,y1)
P2(x2,y2)
P
(1)
M
中点坐标公式:
)
2
,
2
(
2
1
2
1
y
y
x
x
+
+
典例讲解
x
y
O
P1
P2
P
x
y
O
P1
P2
P
例11、设点P是线段P1P2上的一点,P1、P2的坐标分别是
。
(1)当点P是线段P1P2的中点时,求点P的坐标;
(2)当点P是线段P1P2的一个三等分点时,求点P的坐标。
典例讲解
解:
x
y
O
P1
P2
P
拓 展
你能根据前面的结论推导三角形的重心坐标公式吗?
A
B
C
E
F
D
G
则点G的坐标为
的三个顶点的坐标分别为
点G为重心,
拓 展
典例讲解
例12、已知点点在圆上运动,
求的重心的轨迹方程.
设的重心为则
解得: (1)
又因点在圆上运动,所以
将(1)式代入(2)式得:
所以的重心的轨迹方程为.
解析
素养提炼
素养提炼
当堂练习
1.已知则 =( )
A.(3,0) B.(2,1) C.(3,3) D.(3,3)
2.若三点,则B,则 ( )
A. 1 B. 3 C. D. 51
D
B
3.已知,且// , 等于 ( )
A.(5, 10) B.(4, 8) C.(3, 6) D.(2, 4)
4.已知点,若,则 点P的坐标是__________.
B
归纳小结
作 业
课本35页 练习:1、2、3、5
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
