人教A版(2019)高中数学必修第二册 《平面向量的正交分解及加、减运算的坐标表示》名师课件(共38张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 《平面向量的正交分解及加、减运算的坐标表示》名师课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 00:00:00 | ||
图片预览







文档简介
(共38张PPT)
复习引入
平面向量的基本定理
其实质:同一平面内任一向量都可以用两个不共线向量来表示.
=
人教A版同步教材名师课件
平面向量的正交分解及加、减运算的坐标表示
学习目标
学 习 目 标 核心素养
通过平面向量基本定理及正交分解,可以导出平面向量的坐标表示,利用向量的加、减法及数乘运算法则,会导出平面向量的加、减法及数乘运算的坐标表示. 数学抽象
掌握向量的三种表示方法:几何表示法、字母表示法、坐标表示法. 直观想象
理解向量的坐标运算是一种代数运算,其加、减及数乘的实质是坐标之间的运算. 逻辑推理
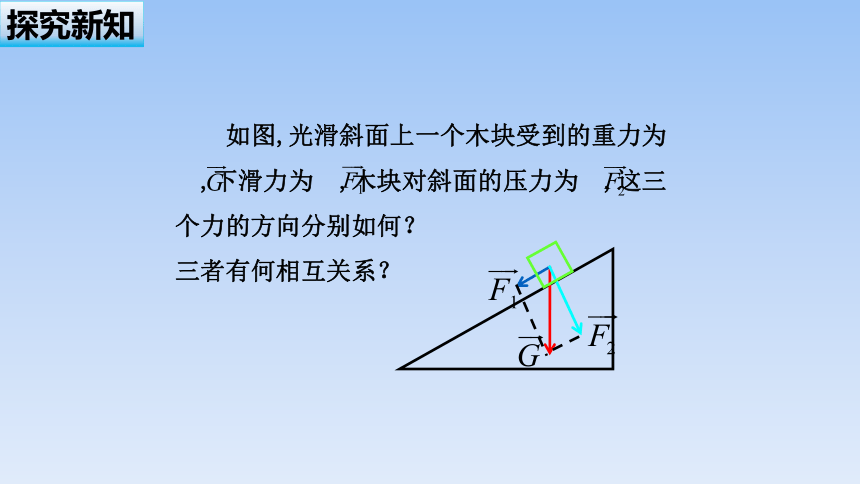
如图,光滑斜面上一个木块受到的重力为 ,下滑力为 ,木块对斜面的压力为 ,这三个力的方向分别如何?
三者有何相互关系?
探究新知
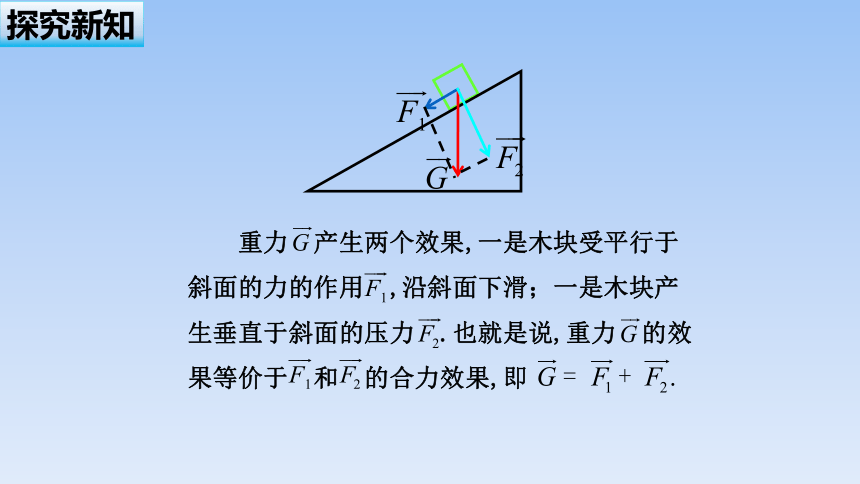
重力 产生两个效果,一是木块受平行于斜面的力的作用 ,沿斜面下滑;一是木块产生垂直于斜面的压力 .也就是说,重力 的效果等价于 和 的合力效果,即
探究新知
在物理中,力是一个向量,力的合成就是向量的加法运算.力也可以分解,任何一个大小不为零的力,都可以分解成两个不同方向的分力之和.将这种力的分解拓展到向量中来,就会形成一个新的数学理论.
探究新知
把一个向量分解为两个互相垂直的向量,叫做把向量正交分解.
平面向量的正交分解
探究新知
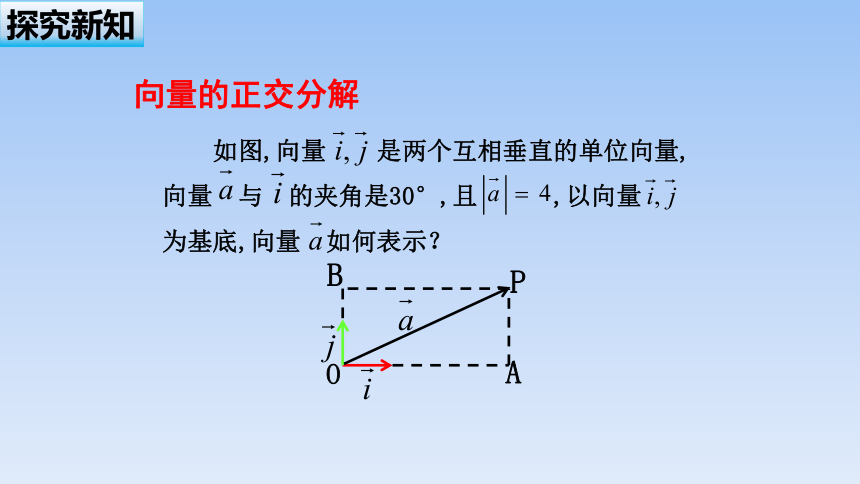
如图,向量 是两个互相垂直的单位向量,向量 与 的夹角是30°,且 ,以向量 为基底,向量 如何表示?
B
O
A
P
向量的正交分解
探究新知
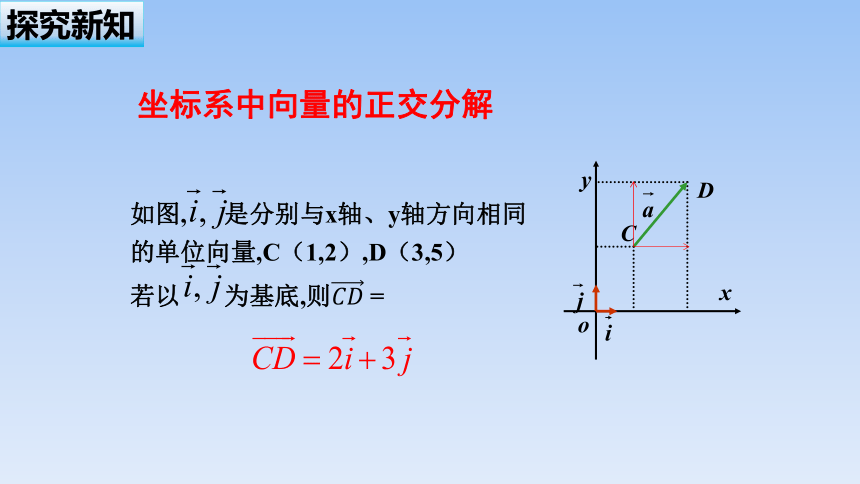
如图, 是分别与x轴、y轴方向相同
的单位向量,C(1,2),D(3,5)
若以 为基底,则 =
坐标系中向量的正交分解
探究新知
如图, 是分别与x轴、y轴方向相同
的单位向量,若以 为基底,则
平面向量的坐标表示
探究新知
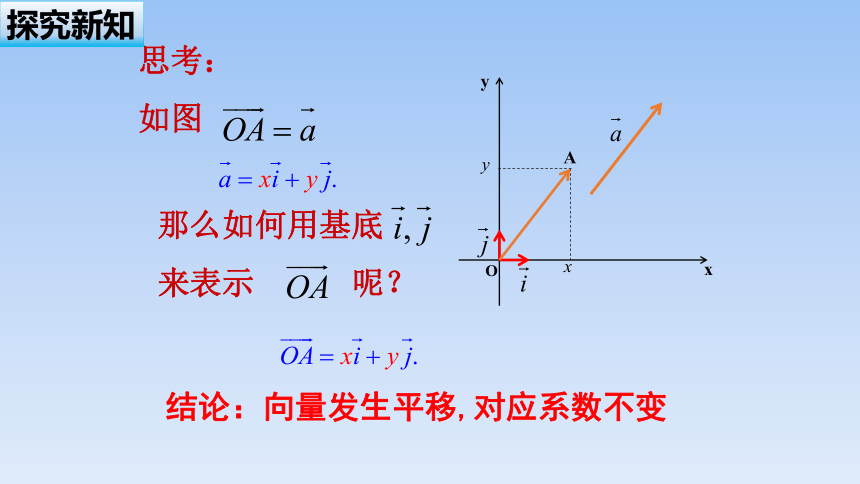
思考:
如图
O
x
y
A
那么如何用基底
来表示 呢?
结论:向量发生平移,对应系数不变
探究新知
①
其中,x叫做 在x轴上的坐标,y叫做 在y轴上的坐标,①式叫做向量的坐标表示.
这样,平面内的任一向量 都可由x,y唯一确定,我们把(x,y)叫做向量 的(直角)坐标,记作
探究新知
如图, 是分别与x轴、y轴方向相同
的单位向量,C(1,2),D(3,5)
若以 为基底,则 =
平面向量的坐标表示
(1,0)
(0,1)
(0,0)
特别地:
探究新知
概念理解
O
x
y
A
1.以原点O为起点作 ,点A的位置是唯一确定的吗?由谁确定
由 唯一确定.
探究新知
2.点A的坐标与向量 的坐标的关系?
两者相同
向量
坐标(x ,y)
一 一 对 应
O
x
y
A
探究新知
1
2
3
4
-1
-5
-2
-3
-4
x
y
5
0
1
2
3
4
-1
-2
-3
o
若已知 =(1 ,3) , =(5 ,1),
a
b
如何求 + , -- 的坐标呢?
a
b
a
b
a
b
C
(6,4)
- =(x1-x2 ,y1-y2)
b
a
(x1,y1)
(x2,y2)
+
b
a
=(x1 +y1 )
+(x2 +y2 )
=(x1 + x2 ) + ( y1+ y2 )
猜想:
+ =(x1+x2 ,y1+y2)
b
a
证明:
=(x1 , ) + ( , y2 )
=(x1 +y1 )
+(x2 +y2 )
重点
?
已知两个向量的坐标如何求它们和向量与差向量的坐标呢
探究新知
平面向量的坐标运算法则
结论:两个向量和(差)的坐标分别等于这两个向量相应坐标的和(差).
探究新知
探究:将表示向量的有向线段的起点放在坐标原点后有何结论呢?
a
x
y
o
A
1
2
3
1
2
3
结论:以原点O为起点的向量
OA的坐标与点A的坐标相同
此时向量坐标就由这条有向线段的终点坐标唯一确定了.
A(2,3)
探究新知
已知 ,求 的坐标.
O
x
y
B(x2,y2)
A(x1,y1)
结论:一个向量的坐标等于表示此向量的终点的坐标减去始点的坐标。
问题:若已知点A、点B的坐标,如何求向量AB的坐标呢?
探究新知
典例讲解
例1、用基底分别表示向量并求出它们的坐标.
-4 -3 -2 -1 1 2 3 4
A
B
1
2
-2
-1
x
y
4
5
3
典例讲解
方法归纳
1.在同一直角坐标系内画出下列向量.
1
2
-1
3
变式训练
解析
例2、已知O是坐标原点,点A在第一象限,||=4,∠xOA=60°,
(1)求向量的坐标;
(2)若B(,-1),求的坐标.
(1)设点A(x,y),则x= || cos 60°=4cos 60°=2,
y= || sin 60°=4sin 60°=6,
即A(2,6),所以=(2,6).
(2) =(2,6)-(,-1)=(,7).
典例讲解
解析
方法归纳
(1)在求一个向量时,可以首先求出这个向量的起点坐标A(x1,y1)和终点坐标B(x2,y2),则=(x1,y1),=(x2,y2),=-=(x2,y2)-(x1,y1)=(x2-x1,
y2-y1).
(2)求一个点的坐标,可以转化为求该点相对于坐标原点的位置向量的坐标.
[注意] 点的坐标不能直接参与向量的坐标表示及运算.
求点和向量坐标的常用方法
2.如图,取与x轴、y轴同向的两个单位向量i,j作为基底,分别用i,j表示并求出它们的坐标.
变式训练
由图形可知,=6i+2j,=2i+4j,=-4i+2j,它们的坐标表示为=(6,2), =(2,4), =(-4,2).
解析
例3、(1)已知点A(0,1),B(3,2),向量=(-4,-3),则向量=( )
A.(-7,-4) B.(7,4) C.(-1,4) D.(1,4)
(2)已知向量的坐标分别是(-1,2),(3,-5),求的坐标.
典例讲解
(1)法一:设,则=(-4,-3),所以从而
法二:
(2) =(-1,2)+(3,-5)=(2,-3),=(-1,2)-(3,-5)=(-4,7),
=3(-1,2)=(-3,6),=2(-1,2)+3(3,-5)=(-2,4)+(9,-15)=(7,-11).
解析
(1)若已知向量的坐标,则直接应用两个向量和、差及向量数乘的运算法则进行.
(2)若已知有向线段两端点的坐标,则必须先求出向量的坐标,然后再进行向量的坐标运算.
(3)向量的线性坐标运算可类比数的运算进行.
平面向量坐标(线性)运算的方法
方法归纳
3.(1)已知向量=(2,1),=(1,-2),若m+nm,n∈R),则m-n的值为________.
(2)已知A(2,-4),B(-1,3),C(3,4),若=2+3,求点M的坐标.
变式训练
(1)因为 m+n=(2m+n,m-2n)=(9,-8),
所以所以所以m-n=2-5=-3.故填-3.
(2)由A(2,-4),B(-1,3),C(3,4),得=(2-3,-4-4)=(-1,-8),=(-1-3,3-4)
=(-4,-1),
所以=2+3=2(-1,-8)+3(-4,-1)=(-2,-16)+(-12,-3)=(-14,-19).
解析
3.(1)已知向量=(2,1),=(1,-2),若m+nm,n∈R),则m-n的值为________.
(2)已知A(2,-4),B(-1,3),C(3,4),若=2+3,求点M的坐标.
变式训练
解析
设点M的坐标为(x,y),则=(x-3,y-4).
由向量相等坐标相同可得解得
所以点M的坐标为(-11,-15).
例4、已知点O(0,0),A(1,2),B(4,5),及= +t .
(1)t为何值时,点P在x轴上?点P在y轴上?点P在第二象限?
(2)四边形OABP能为平行四边形吗?若能,求出t的值;若不能,请说明理由.
(1) = +t =(1,2)+t(3,3)
=(1+3t,2+3t).
若点P在第二象限,则
所以-<t<-.
若点P在x轴上,则2+3t=0,所以t=-.
若点P在y轴上,则1+3t=0,所以t=-.
该方程组无解.
故四边形OABP不能为平行四边形.
(2)=(1,2),=(3-3t,3-3t).
若四边形OABP为平行四边形,
则=,所以
变式训练
若保持本例条件不变,问t为何值时,B为线段AP的中点?
由= +t ,得= t .
所以当t=2时,= ,B为线段AP的中点.
典例讲解
解析
(1)向量的坐标含有两个量:横坐标和纵坐标,如果纵坐标或横坐标是一个变量,则表示向量的点的坐标的位置会随之改变.
(2)解答这类由参数决定点的位置的题目,关键是列出满足条件的含参数的方程(组),解这个方程(组),就能达到解题的目的.
向量中含参数问题的求解策略
方法归纳
4.已知=(-1,2),=(1,-1),=(3,-2),且有=p+q,试求实数p,q的值.
变式训练
因为=(-1,2),=(1,-1),
所以p+q=p(-1,2)+q(1,-1)=(-p+q,2p-q).
因为=p+q,所以解得
故p,q的值分别为1,4.
解析
素养提炼
1.向量坐标
(1)平面向量的坐标只有当起点在原点时,向量的坐标才与向量终点的坐标相同.
(2)给定一个向量,它的坐标是唯一的,对应一对实数,由于向量可以平移,故以这对实数为坐标的向量有无穷多个.
2.平面向量坐标运算的注意点
(1)要弄清楚向量的坐标与表示该向量的有向线段的始点、终点的具体位置无关,只与其相对位置有关.
(2)进行向量的坐标运算时,向量的始点、终点的顺序不能颠倒.
当堂练习
1.已知则下面说法正确的是( )
A.A点的坐标是(2,4)
B.B点的坐标是(2,4)
C.当B是原点时,A点的坐标是(2,4)
D.当A是原点时,B点的坐标是(2,4)
2.设平面向量则= ( )
A.(4,4) B.(5,4) C.(0,2) D.(5,3)
D
B
当堂练习
3.若向量,且A点的坐标为(2,3),则B点的坐标为 ( )
A.(2,6) B.(3,5) C.(1,1) D.(1, 1)
4.已知平行四边形ABCD的三个顶点A,B,C的坐标分别是(2,1),(1,3),(3,4),
则向量的坐标是( )
B
B
归纳小结
平面向量的坐标
表示及运算
平面向量的正交分解
平面向量的坐标表示
平面向量的坐标运算
加法运算
减法运算
作 业
课本30页:练习:1、2、3
复习引入
平面向量的基本定理
其实质:同一平面内任一向量都可以用两个不共线向量来表示.
=
人教A版同步教材名师课件
平面向量的正交分解及加、减运算的坐标表示
学习目标
学 习 目 标 核心素养
通过平面向量基本定理及正交分解,可以导出平面向量的坐标表示,利用向量的加、减法及数乘运算法则,会导出平面向量的加、减法及数乘运算的坐标表示. 数学抽象
掌握向量的三种表示方法:几何表示法、字母表示法、坐标表示法. 直观想象
理解向量的坐标运算是一种代数运算,其加、减及数乘的实质是坐标之间的运算. 逻辑推理
如图,光滑斜面上一个木块受到的重力为 ,下滑力为 ,木块对斜面的压力为 ,这三个力的方向分别如何?
三者有何相互关系?
探究新知
重力 产生两个效果,一是木块受平行于斜面的力的作用 ,沿斜面下滑;一是木块产生垂直于斜面的压力 .也就是说,重力 的效果等价于 和 的合力效果,即
探究新知
在物理中,力是一个向量,力的合成就是向量的加法运算.力也可以分解,任何一个大小不为零的力,都可以分解成两个不同方向的分力之和.将这种力的分解拓展到向量中来,就会形成一个新的数学理论.
探究新知
把一个向量分解为两个互相垂直的向量,叫做把向量正交分解.
平面向量的正交分解
探究新知
如图,向量 是两个互相垂直的单位向量,向量 与 的夹角是30°,且 ,以向量 为基底,向量 如何表示?
B
O
A
P
向量的正交分解
探究新知
如图, 是分别与x轴、y轴方向相同
的单位向量,C(1,2),D(3,5)
若以 为基底,则 =
坐标系中向量的正交分解
探究新知
如图, 是分别与x轴、y轴方向相同
的单位向量,若以 为基底,则
平面向量的坐标表示
探究新知
思考:
如图
O
x
y
A
那么如何用基底
来表示 呢?
结论:向量发生平移,对应系数不变
探究新知
①
其中,x叫做 在x轴上的坐标,y叫做 在y轴上的坐标,①式叫做向量的坐标表示.
这样,平面内的任一向量 都可由x,y唯一确定,我们把(x,y)叫做向量 的(直角)坐标,记作
探究新知
如图, 是分别与x轴、y轴方向相同
的单位向量,C(1,2),D(3,5)
若以 为基底,则 =
平面向量的坐标表示
(1,0)
(0,1)
(0,0)
特别地:
探究新知
概念理解
O
x
y
A
1.以原点O为起点作 ,点A的位置是唯一确定的吗?由谁确定
由 唯一确定.
探究新知
2.点A的坐标与向量 的坐标的关系?
两者相同
向量
坐标(x ,y)
一 一 对 应
O
x
y
A
探究新知
1
2
3
4
-1
-5
-2
-3
-4
x
y
5
0
1
2
3
4
-1
-2
-3
o
若已知 =(1 ,3) , =(5 ,1),
a
b
如何求 + , -- 的坐标呢?
a
b
a
b
a
b
C
(6,4)
- =(x1-x2 ,y1-y2)
b
a
(x1,y1)
(x2,y2)
+
b
a
=(x1 +y1 )
+(x2 +y2 )
=(x1 + x2 ) + ( y1+ y2 )
猜想:
+ =(x1+x2 ,y1+y2)
b
a
证明:
=(x1 , ) + ( , y2 )
=(x1 +y1 )
+(x2 +y2 )
重点
?
已知两个向量的坐标如何求它们和向量与差向量的坐标呢
探究新知
平面向量的坐标运算法则
结论:两个向量和(差)的坐标分别等于这两个向量相应坐标的和(差).
探究新知
探究:将表示向量的有向线段的起点放在坐标原点后有何结论呢?
a
x
y
o
A
1
2
3
1
2
3
结论:以原点O为起点的向量
OA的坐标与点A的坐标相同
此时向量坐标就由这条有向线段的终点坐标唯一确定了.
A(2,3)
探究新知
已知 ,求 的坐标.
O
x
y
B(x2,y2)
A(x1,y1)
结论:一个向量的坐标等于表示此向量的终点的坐标减去始点的坐标。
问题:若已知点A、点B的坐标,如何求向量AB的坐标呢?
探究新知
典例讲解
例1、用基底分别表示向量并求出它们的坐标.
-4 -3 -2 -1 1 2 3 4
A
B
1
2
-2
-1
x
y
4
5
3
典例讲解
方法归纳
1.在同一直角坐标系内画出下列向量.
1
2
-1
3
变式训练
解析
例2、已知O是坐标原点,点A在第一象限,||=4,∠xOA=60°,
(1)求向量的坐标;
(2)若B(,-1),求的坐标.
(1)设点A(x,y),则x= || cos 60°=4cos 60°=2,
y= || sin 60°=4sin 60°=6,
即A(2,6),所以=(2,6).
(2) =(2,6)-(,-1)=(,7).
典例讲解
解析
方法归纳
(1)在求一个向量时,可以首先求出这个向量的起点坐标A(x1,y1)和终点坐标B(x2,y2),则=(x1,y1),=(x2,y2),=-=(x2,y2)-(x1,y1)=(x2-x1,
y2-y1).
(2)求一个点的坐标,可以转化为求该点相对于坐标原点的位置向量的坐标.
[注意] 点的坐标不能直接参与向量的坐标表示及运算.
求点和向量坐标的常用方法
2.如图,取与x轴、y轴同向的两个单位向量i,j作为基底,分别用i,j表示并求出它们的坐标.
变式训练
由图形可知,=6i+2j,=2i+4j,=-4i+2j,它们的坐标表示为=(6,2), =(2,4), =(-4,2).
解析
例3、(1)已知点A(0,1),B(3,2),向量=(-4,-3),则向量=( )
A.(-7,-4) B.(7,4) C.(-1,4) D.(1,4)
(2)已知向量的坐标分别是(-1,2),(3,-5),求的坐标.
典例讲解
(1)法一:设,则=(-4,-3),所以从而
法二:
(2) =(-1,2)+(3,-5)=(2,-3),=(-1,2)-(3,-5)=(-4,7),
=3(-1,2)=(-3,6),=2(-1,2)+3(3,-5)=(-2,4)+(9,-15)=(7,-11).
解析
(1)若已知向量的坐标,则直接应用两个向量和、差及向量数乘的运算法则进行.
(2)若已知有向线段两端点的坐标,则必须先求出向量的坐标,然后再进行向量的坐标运算.
(3)向量的线性坐标运算可类比数的运算进行.
平面向量坐标(线性)运算的方法
方法归纳
3.(1)已知向量=(2,1),=(1,-2),若m+nm,n∈R),则m-n的值为________.
(2)已知A(2,-4),B(-1,3),C(3,4),若=2+3,求点M的坐标.
变式训练
(1)因为 m+n=(2m+n,m-2n)=(9,-8),
所以所以所以m-n=2-5=-3.故填-3.
(2)由A(2,-4),B(-1,3),C(3,4),得=(2-3,-4-4)=(-1,-8),=(-1-3,3-4)
=(-4,-1),
所以=2+3=2(-1,-8)+3(-4,-1)=(-2,-16)+(-12,-3)=(-14,-19).
解析
3.(1)已知向量=(2,1),=(1,-2),若m+nm,n∈R),则m-n的值为________.
(2)已知A(2,-4),B(-1,3),C(3,4),若=2+3,求点M的坐标.
变式训练
解析
设点M的坐标为(x,y),则=(x-3,y-4).
由向量相等坐标相同可得解得
所以点M的坐标为(-11,-15).
例4、已知点O(0,0),A(1,2),B(4,5),及= +t .
(1)t为何值时,点P在x轴上?点P在y轴上?点P在第二象限?
(2)四边形OABP能为平行四边形吗?若能,求出t的值;若不能,请说明理由.
(1) = +t =(1,2)+t(3,3)
=(1+3t,2+3t).
若点P在第二象限,则
所以-<t<-.
若点P在x轴上,则2+3t=0,所以t=-.
若点P在y轴上,则1+3t=0,所以t=-.
该方程组无解.
故四边形OABP不能为平行四边形.
(2)=(1,2),=(3-3t,3-3t).
若四边形OABP为平行四边形,
则=,所以
变式训练
若保持本例条件不变,问t为何值时,B为线段AP的中点?
由= +t ,得= t .
所以当t=2时,= ,B为线段AP的中点.
典例讲解
解析
(1)向量的坐标含有两个量:横坐标和纵坐标,如果纵坐标或横坐标是一个变量,则表示向量的点的坐标的位置会随之改变.
(2)解答这类由参数决定点的位置的题目,关键是列出满足条件的含参数的方程(组),解这个方程(组),就能达到解题的目的.
向量中含参数问题的求解策略
方法归纳
4.已知=(-1,2),=(1,-1),=(3,-2),且有=p+q,试求实数p,q的值.
变式训练
因为=(-1,2),=(1,-1),
所以p+q=p(-1,2)+q(1,-1)=(-p+q,2p-q).
因为=p+q,所以解得
故p,q的值分别为1,4.
解析
素养提炼
1.向量坐标
(1)平面向量的坐标只有当起点在原点时,向量的坐标才与向量终点的坐标相同.
(2)给定一个向量,它的坐标是唯一的,对应一对实数,由于向量可以平移,故以这对实数为坐标的向量有无穷多个.
2.平面向量坐标运算的注意点
(1)要弄清楚向量的坐标与表示该向量的有向线段的始点、终点的具体位置无关,只与其相对位置有关.
(2)进行向量的坐标运算时,向量的始点、终点的顺序不能颠倒.
当堂练习
1.已知则下面说法正确的是( )
A.A点的坐标是(2,4)
B.B点的坐标是(2,4)
C.当B是原点时,A点的坐标是(2,4)
D.当A是原点时,B点的坐标是(2,4)
2.设平面向量则= ( )
A.(4,4) B.(5,4) C.(0,2) D.(5,3)
D
B
当堂练习
3.若向量,且A点的坐标为(2,3),则B点的坐标为 ( )
A.(2,6) B.(3,5) C.(1,1) D.(1, 1)
4.已知平行四边形ABCD的三个顶点A,B,C的坐标分别是(2,1),(1,3),(3,4),
则向量的坐标是( )
B
B
归纳小结
平面向量的坐标
表示及运算
平面向量的正交分解
平面向量的坐标表示
平面向量的坐标运算
加法运算
减法运算
作 业
课本30页:练习:1、2、3
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
