人教A版(2019)高中数学必修第二册 6.3.2平面向量的正交分解及坐标表示教学设计(2)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 6.3.2平面向量的正交分解及坐标表示教学设计(2) |  | |
| 格式 | docx | ||
| 文件大小 | 108.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 19:21:18 | ||
图片预览

文档简介
6.3.2 平面向量的正交分解及坐标表示教学设计
本节内容是平面向量一种新的表示方:向量的坐标表示,是本章的重点内容之一,也是培养学生自主学习能力的良好题材.引入向量的坐标表示可使向量运算完全代数化,将数与形紧密结合起来,这就可以使很多几何问题的解答转化为学生熟知的数量运算.
课程目标
掌握平面向量的正交分解及其坐标表示;
2.通过学习平面向量的正交分解及其坐标表示,使学生认识事物之间的相互联系,培养学生辨证思维能力.
数学学科素养
1.数学抽象:平面向量的坐标表示;
2.逻辑推理:根据正交分解和平面向量共线定理推导出平面向量的坐标表示;
3.数学建模:数形结合,将几何问题转化为代数问题解决.
重点:向量的坐标表示;
难点:向量的坐标表示的理解.
教学方法:以学生为主体,小组为单位,采用诱思探究式教学,精讲多练。
教学工具:多媒体。
情景导入
问题:由平面向量基本定理,我们知道,在平面直角坐标系,每一个点都可用一对有序实数(即它的坐标)表示,对直角坐标平面内的每一个向量,如何表示?
要求:让学生自由发言,教师不做判断。而是引导学生进一步观察,研探.
二、预习课本,引入新课
阅读课本27-29页,思考并完成以下问题
1、怎样分解一个向量才为正交分解?
2、平面向量怎样用坐标表示?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
三、新知探究
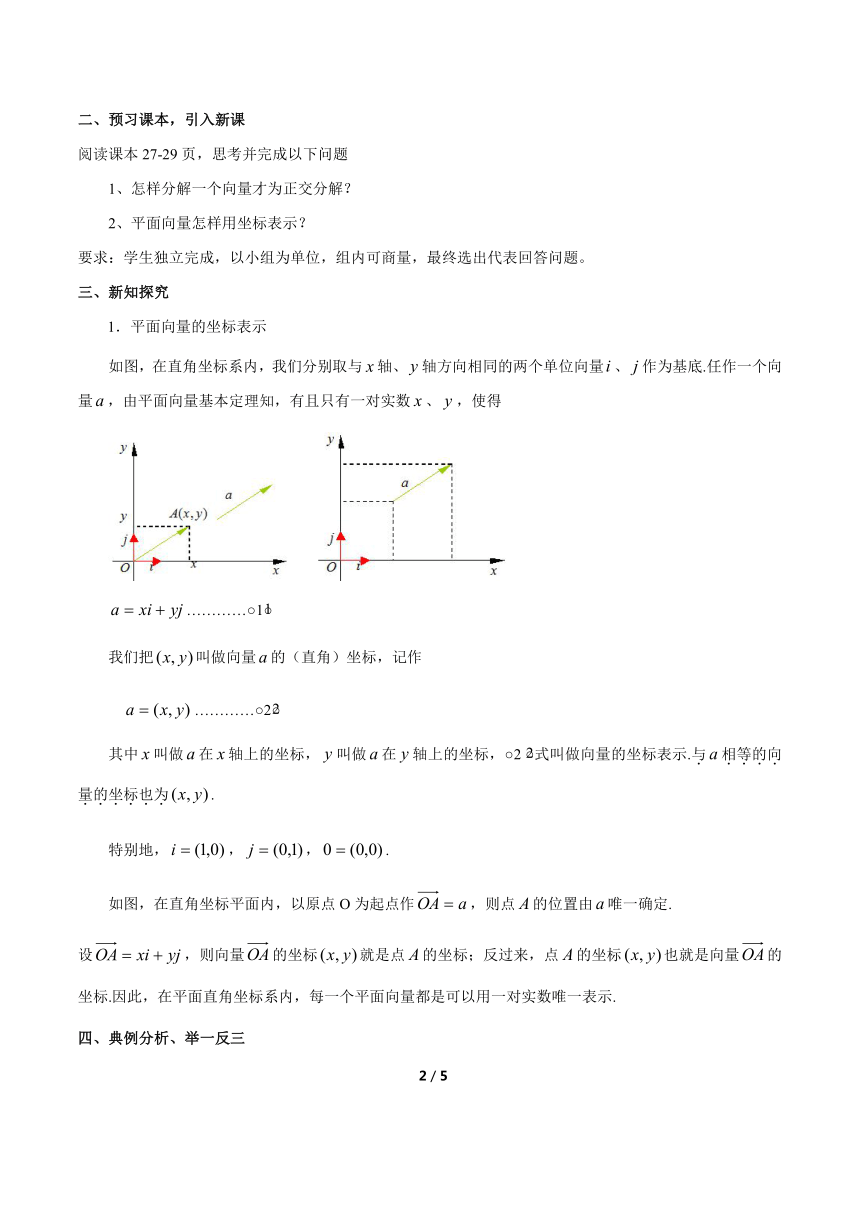
1.平面向量的坐标表示
如图,在直角坐标系内,我们分别取与轴、轴方向相同的两个单位向量、作为基底.任作一个向量,由平面向量基本定理知,有且只有一对实数、,使得
…………○1
我们把叫做向量的(直角)坐标,记作
…………○2
其中叫做在轴上的坐标,叫做在轴上的坐标,○2式叫做向量的坐标表示.与相等的向量的坐标也为.
特别地,,,.
如图,在直角坐标平面内,以原点O为起点作,则点的位置由唯一确定.
设,则向量的坐标就是点的坐标;反过来,点的坐标也就是向量的坐标.因此,在平面直角坐标系内,每一个平面向量都是可以用一对实数唯一表示.
四、典例分析、举一反三
题型一 向量的减法运算
例1 如图,向量a,b,c的坐标分别是________,________,_______________.
【答案】a=(-4,0); b=(0,6);c=(-2,-5).
【解析】将各向量分别向基底i,j所在直线分解,则a=-4i+0·j,∴a=(-4,0);b=0·i+6j,∴b=(0,6);c=-2i-5j,∴c=(-2,-5).
例2 如图所示,在边长为1的正方形ABCD中,AB与x轴正半轴成30°角.求点B和点D的坐标和与的坐标.
【答案】B. D.=,=.
【解析】由题知B,D分别是30°,120°角的终边与单位圆的交点.设B(x1,y1),D(x2,y2).由三角函数的定义,得
x1=cos30°=,y1=sin30°=,∴B.
x2=cos120°=-,y2=sin120°=,∴D.
∴=,=.
解题技巧(求点和向量坐标的方法)
(1)求一个点的坐标,可以转化为求该点相对于坐标原点的位置向量的坐标.
(2)在求一个向量时,可以首先求出这个向量的起点坐标和终点坐标,再运用终点坐标减去起点坐标得到该向量的坐标.
跟踪训练一
1.已知e1=(1,2),e2=(-2,3),a=(-1,2),试以e1,e2为基底,将a分解成λ1e1+λ2e2的形式为____________.
【答案】a=e1+e2.
【解析】设a=λ1e1+λ2e2(λ1,λ2∈R),则(-1,2)=λ1(1,2)+λ2(-2,3)=(λ1-2λ2,2λ1+3λ2).
∴解得∴a=e1+e2.
2. 已知O是坐标原点,点A在第一象限,||=4,∠xOA=60°,
(1)求向量的坐标;
(2)若B(,-1),求的坐标.
【答案】(1)=(2,6).(2)= (,7).
【解析】(1)设点A(x,y),则x=4cos60°=2,
y=4sin60°=6,即A(2,6),=(2,6).
(2)=(2,6)-(,-1)=(,7).
五、课堂小结
让学生总结本节课所学主要知识及解题技巧
六、板书设计
七、作业
课本37页习题6.3的15题.
本节内容是平面向量定理的一种延伸,比较简单,学生掌握起来较容易.引入向量的坐标表示可使向量运算完全代数化,将数与形紧密结合起来,这就可以使很多几何问题的解答转化为学生熟知的数量运算.
1 / 5
本节内容是平面向量一种新的表示方:向量的坐标表示,是本章的重点内容之一,也是培养学生自主学习能力的良好题材.引入向量的坐标表示可使向量运算完全代数化,将数与形紧密结合起来,这就可以使很多几何问题的解答转化为学生熟知的数量运算.
课程目标
掌握平面向量的正交分解及其坐标表示;
2.通过学习平面向量的正交分解及其坐标表示,使学生认识事物之间的相互联系,培养学生辨证思维能力.
数学学科素养
1.数学抽象:平面向量的坐标表示;
2.逻辑推理:根据正交分解和平面向量共线定理推导出平面向量的坐标表示;
3.数学建模:数形结合,将几何问题转化为代数问题解决.
重点:向量的坐标表示;
难点:向量的坐标表示的理解.
教学方法:以学生为主体,小组为单位,采用诱思探究式教学,精讲多练。
教学工具:多媒体。
情景导入
问题:由平面向量基本定理,我们知道,在平面直角坐标系,每一个点都可用一对有序实数(即它的坐标)表示,对直角坐标平面内的每一个向量,如何表示?
要求:让学生自由发言,教师不做判断。而是引导学生进一步观察,研探.
二、预习课本,引入新课
阅读课本27-29页,思考并完成以下问题
1、怎样分解一个向量才为正交分解?
2、平面向量怎样用坐标表示?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
三、新知探究
1.平面向量的坐标表示
如图,在直角坐标系内,我们分别取与轴、轴方向相同的两个单位向量、作为基底.任作一个向量,由平面向量基本定理知,有且只有一对实数、,使得
…………○1
我们把叫做向量的(直角)坐标,记作
…………○2
其中叫做在轴上的坐标,叫做在轴上的坐标,○2式叫做向量的坐标表示.与相等的向量的坐标也为.
特别地,,,.
如图,在直角坐标平面内,以原点O为起点作,则点的位置由唯一确定.
设,则向量的坐标就是点的坐标;反过来,点的坐标也就是向量的坐标.因此,在平面直角坐标系内,每一个平面向量都是可以用一对实数唯一表示.
四、典例分析、举一反三
题型一 向量的减法运算
例1 如图,向量a,b,c的坐标分别是________,________,_______________.
【答案】a=(-4,0); b=(0,6);c=(-2,-5).
【解析】将各向量分别向基底i,j所在直线分解,则a=-4i+0·j,∴a=(-4,0);b=0·i+6j,∴b=(0,6);c=-2i-5j,∴c=(-2,-5).
例2 如图所示,在边长为1的正方形ABCD中,AB与x轴正半轴成30°角.求点B和点D的坐标和与的坐标.
【答案】B. D.=,=.
【解析】由题知B,D分别是30°,120°角的终边与单位圆的交点.设B(x1,y1),D(x2,y2).由三角函数的定义,得
x1=cos30°=,y1=sin30°=,∴B.
x2=cos120°=-,y2=sin120°=,∴D.
∴=,=.
解题技巧(求点和向量坐标的方法)
(1)求一个点的坐标,可以转化为求该点相对于坐标原点的位置向量的坐标.
(2)在求一个向量时,可以首先求出这个向量的起点坐标和终点坐标,再运用终点坐标减去起点坐标得到该向量的坐标.
跟踪训练一
1.已知e1=(1,2),e2=(-2,3),a=(-1,2),试以e1,e2为基底,将a分解成λ1e1+λ2e2的形式为____________.
【答案】a=e1+e2.
【解析】设a=λ1e1+λ2e2(λ1,λ2∈R),则(-1,2)=λ1(1,2)+λ2(-2,3)=(λ1-2λ2,2λ1+3λ2).
∴解得∴a=e1+e2.
2. 已知O是坐标原点,点A在第一象限,||=4,∠xOA=60°,
(1)求向量的坐标;
(2)若B(,-1),求的坐标.
【答案】(1)=(2,6).(2)= (,7).
【解析】(1)设点A(x,y),则x=4cos60°=2,
y=4sin60°=6,即A(2,6),=(2,6).
(2)=(2,6)-(,-1)=(,7).
五、课堂小结
让学生总结本节课所学主要知识及解题技巧
六、板书设计
七、作业
课本37页习题6.3的15题.
本节内容是平面向量定理的一种延伸,比较简单,学生掌握起来较容易.引入向量的坐标表示可使向量运算完全代数化,将数与形紧密结合起来,这就可以使很多几何问题的解答转化为学生熟知的数量运算.
1 / 5
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
