15.3等腰三角形(2课时)
图片预览




文档简介
课件34张PPT。15.3 等腰三角形第1课时
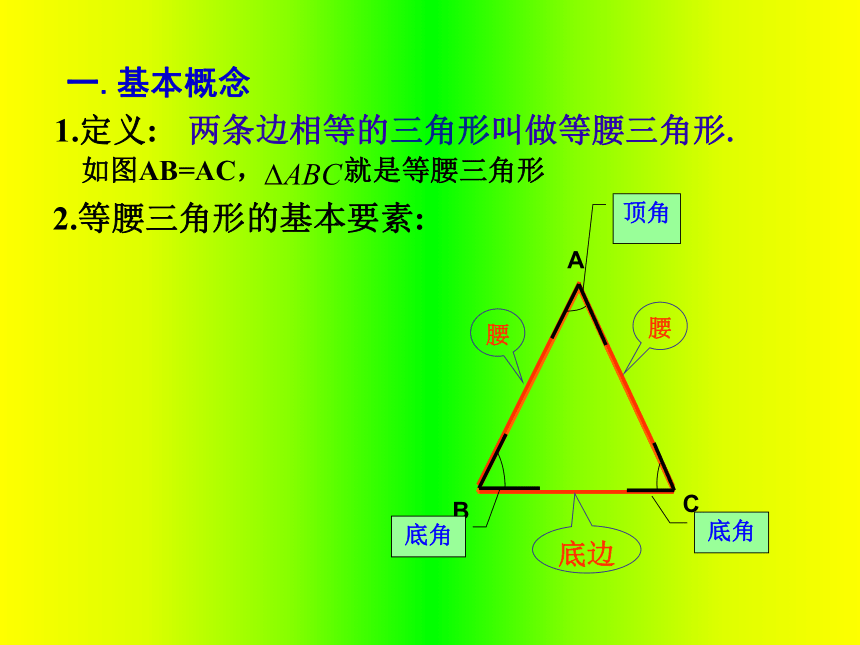
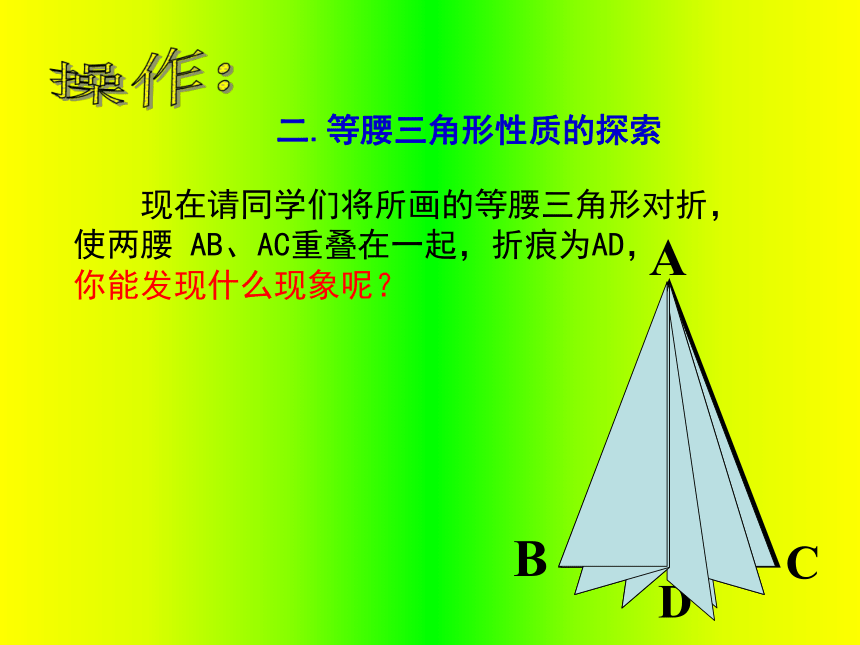
等腰三角形的性质一.基本概念 1.定义:两条边相等的三角形叫做等腰三角形. 如图AB=AC, 就是等腰三角形 2.等腰三角形的基本要素:操作: 现在请同学们将所画的等腰三角形对折,
使两腰 AB、AC重叠在一起,折痕为AD,
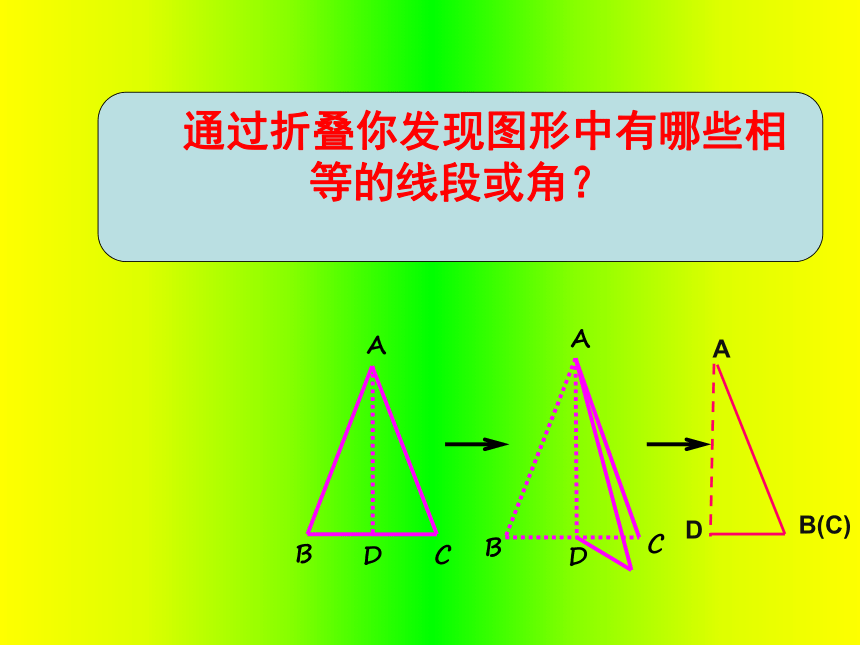
你能发现什么现象呢?二.等腰三角形性质的探索BACD 通过折叠你发现图形中有哪些相等的线段或角?(1)、等腰三角形是轴对称图形(2)、∠ B =∠ C,(3)、BD = CD,(4)、∠ADB = ∠ADC = 90°,(5)、∠BAD = ∠CAD ,由上述结论(2)可得如下性质:定理1 等腰三角形的两底角相等.简称“等边对等角”.由上述结论(3)、(4)、(5)可得如下性质:定理2 等腰三角形顶角的平分线垂直平分底边.(“三线合一”)归纳:即两底角相等即AD 为底边上的中线即AD为底边上的高即AD为顶角平分线CDBA1、(1) 在ΔABC中,∵AB=AC,
∴ ∠B=∠C( )等边对等角① ∵AD⊥BC,
∴∠____ = ∠____,___= ___ ② ∵AD是中线,∴___⊥___ ,∠____ =∠____③∵AD是角平分线,
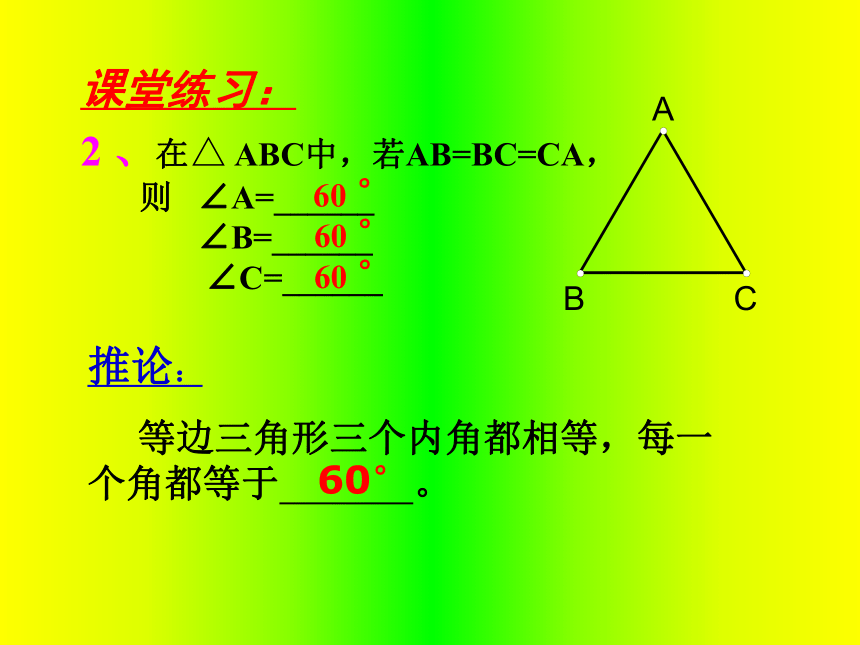
∴___ ⊥___ ,___ =___BAD CADBD CD AD BC AD BCBAD CADBD CD(2) 在△ABC中, AB=AC时, 课堂练习:(三线合一)2 、在△ ABC中,若AB=BC=CA,
则 ∠A=______
∠B=______
∠C=______
推论:
等边三角形三个内角都相等,每一个角都等于 。课堂练习:60 °60 °60 °60°
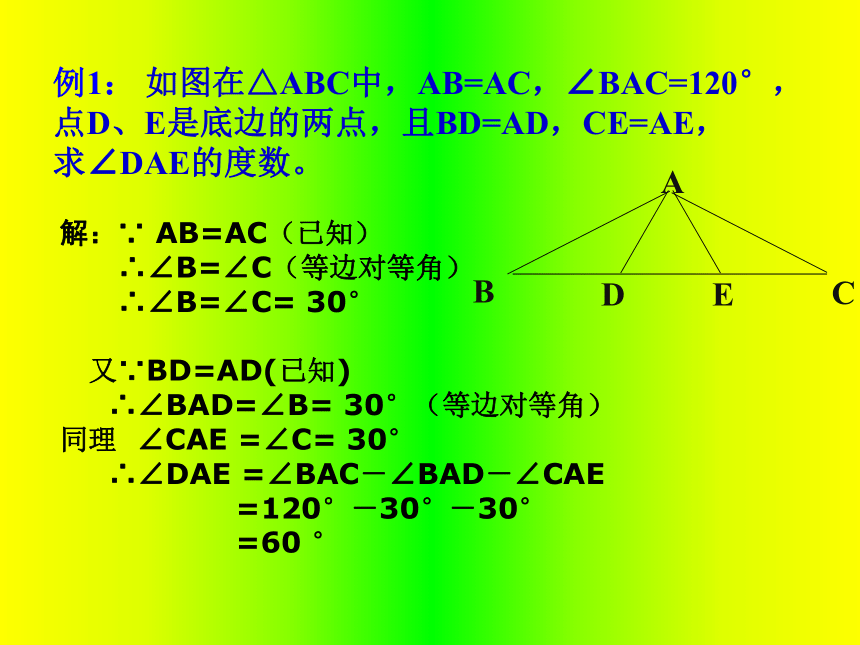
解:∵ AB=AC(已知)
∴∠B=∠C(等边对等角)
∴∠B=∠C= 30°
又∵BD=AD(已知)
∴∠BAD=∠B= 30°(等边对等角)
同理 ∠CAE =∠C= 30°
∴∠DAE =∠BAC-∠BAD-∠CAE
=120°-30°-30°
=60 °例1: 如图在△ABC中,AB=AC,∠BAC=120°,点D、E是底边的两点,且BD=AD,CE=AE,
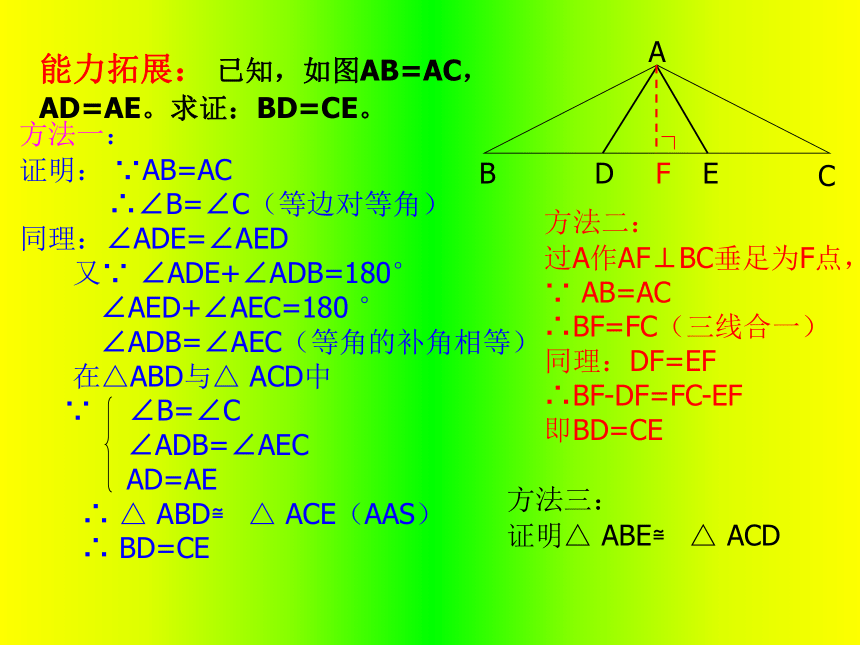
求∠DAE的度数。能力拓展: 已知,如图AB=AC,AD=AE。求证:BD=CE。EDCBA方法一:
证明: ∵AB=AC
∴∠B=∠C(等边对等角)
同理:∠ADE=∠AED
又∵ ∠ADE+∠ADB=180°
∠AED+∠AEC=180 °
∠ADB=∠AEC(等角的补角相等)
在△ABD与△ ACD中
∵ ∠B=∠C
∠ADB=∠AEC
AD=AE
∴ △ ABD≌ △ ACE(AAS)
∴ BD=CE方法二:
过A作AF⊥BC垂足为F点,
∵ AB=AC
∴BF=FC(三线合一)
同理:DF=EF
∴BF-DF=FC-EF
即BD=CEF∟方法三:
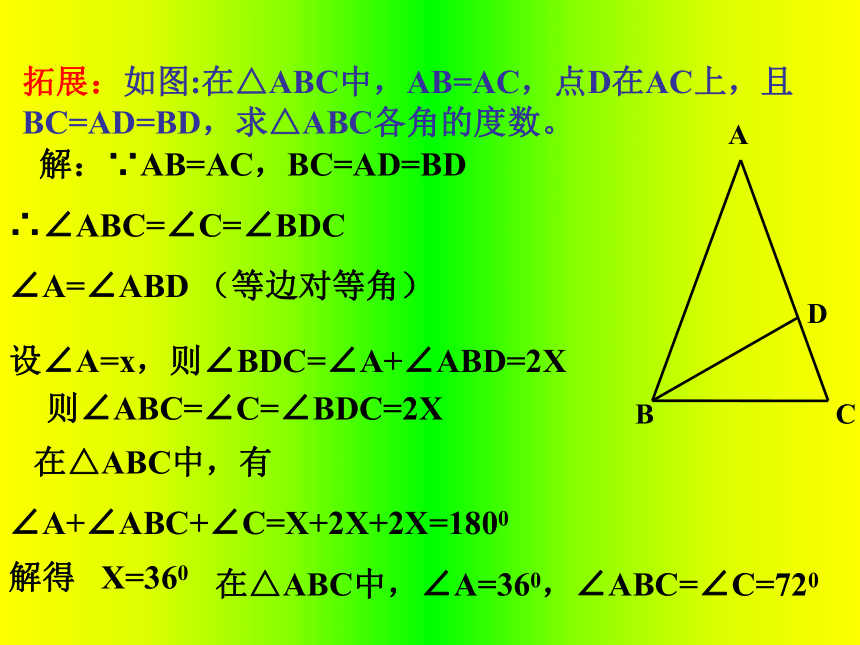
证明△ ABE≌ △ ACD拓展:如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。解:∵AB=AC,BC=AD=BD∴∠ABC=∠C=∠BDC
∠A=∠ABD (等边对等角)设∠A=x,则∠BDC=∠A+∠ABD=2X则∠ABC=∠C=∠BDC=2X 在△ABC中,有
∠A+∠ABC+∠C=X+2X+2X=1800解得 X=360在△ABC中,∠A=360,∠ABC=∠C=720⒈等腰三角形一个底角为40°,它的顶角为______.⒉等腰三角形一顶角为40°,它的另外两个底角为
__________________.⒊等腰三角形一个角为40°,它的另外两个角为___________.100 °100°,40 °
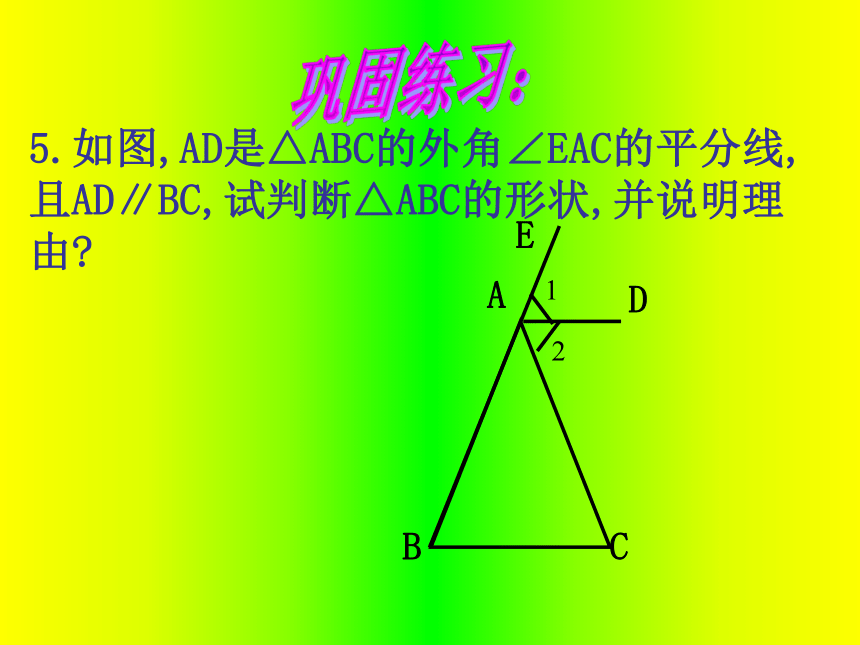
或70 °,70 ° 70°,70°4.等腰三角形一个角为120°,它的另外两个角为 . 30°30°巩固练习:5.如图,AD是△ABC的外角∠EAC的平分线,且AD∥BC,试判断△ABC的形状,并说明理由? BDACE12巩固练习:6.已知:如图,AD∥BC,BD平分∠ABC,试判断△ABD的形状,并说明理由?C巩固练习:7.如图,在等腰△ABC中,AB=AC,两底角的平分线BE和CD相交于点O,那么△OBC是什么三角形?为什么?ABCEDO巩固练习:8.如图,在△ABC中,已知∠ABC=∠ACB,BF平分∠ABC,CF平分∠ACB,EG∥BC.请想想看,由以上条件,你能推导出什么结论?并说明理由.ABCF巩固练习:9.如图,△ABC中,∠C=90°,AC=BC,AD是角平分线。求证:AB=AC+DC。ABCED巩固练习:10、如图,已知AB=AC,EB=EC,
结论∠ABE= ∠ACE是否正确?
说明理由。巩固练习:小结:1、等腰三角形的性质:等边对等角2、 等腰三角形顶角的平分线垂直平分底边(三线合一)本节课你学到了什么? 4、利用等腰三角形的“三线合一”性质作辅助线(顶角的平分线、底边上的高、底边上的中线),帮助我们解决实际问题。3、等边三角形三个内角相等,每一个内角都等于60°15.3 等腰三角形第2课时
等腰三角形的判定等腰三角形的性质?1.等腰三角形的两底角相等(简称“等边对等角”)
2.等腰三角形顶角的平分线、底边上的中线 和底边上的高互相重合(简称“三线合一”) 思考 :1、如图:ΔABC中,已知AB=AC,
∠ B= ∠ C(在同一个三角形中,
等边对等角).
2、反过来:在ΔABC中,∠ B= ∠ C,
AB=AC成立吗?
已知:ΔABC中,∠B=∠C求证:AB=AC证明:作∠BAC的平分线AD在ΔBAD和ΔCAD中,∠BAD=∠CAD,
∠B=∠C,
AD=AD∴ ΔBAD≌ ΔCAD(AAS)∴AB=AC已知在一个三角形中,等角对等边定理 有两个角相等的三角形是
等腰三角形.简称(“等角对等边”) 在△ABC中, ∵∠B=∠C ( ) ∴ AC=AB. ( )用符号语言表示为:这又是一个判定两条线段相等根据之一.
归纳:由上述定理我们可以得到什么启示:已知:如图,⊿ABC中, ∠ A=∠B=∠C
求证:AB=AC=BC
证明:在⊿ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理CA=AB
∴BC=CA=AB
推论1 三个角都相等的三角形是等边三角形。已知: ⊿ABC中,AB=AC, ∠ A=600。
求证:AB=AC=BC证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ A=600
∴ ∠B=∠C = 600
∴AB=AC=BC
已知: ⊿ABC中,AB=AC, ∠B=600。
求证:AB=AC=BC证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ B=600
∴ ∠C = 600
∴∠ A=600
∴AB=AC=BC
推论2 有一个角是600的等腰三角形是等边三角形。 如图:△ABC是直角三角形,其中,∠C=90°
∠A=30°,延长BC到点D,使BC=DC,则△ABD是等边三角形。则AB=BD=AD=1/2BC。 ABDC30°定理 在直角三角形中,
如果一个锐角等于30°,
那么它所对的直角边等
于斜边的一半。
问:如图,下列推理正确吗? (等角对等边)(等角对等边)错,因为都不是在同一个三角形中。练一练:解: ∵ ∠ DAC= ∠ ACB+ ∠ ABC
(三角形外角的性质)∴ ∠ ABC= ∠ DAC -∠ ACB
=60 °- 30 ° =30 °∵ ∠ ABC= ∠ ACB∴ AB=AC(在同一个三角形中, 等角对等边)即AC的长就是河宽。 范例讲解:例1:一次数学实践活动的内容是测量河宽,如图,即测量A, B之间的距离。小明想出了一个方法:从点A出发,沿着与直线AB成60 °角的AC方向前进至C , 在C处测得∠ C= 30 °,量出AC的长,它就是河的宽度。这个方法正确吗?请说明理由。想一想:还有其它测量河宽的方法吗?例2:已知,如图等边△AEB与等边△BCD在线段AC的同侧。 求证: △ABD≌△EBCA B C DE变式:已知如图△ABD与△ACE均为等边三角形,求证:DC=BE想一想:
你还能写出哪些结论
例3:如图,已知在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD与CE相交于M点。求证:BM=CM。证明:∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∴BD⊥AC于D,CE⊥AB于E
∴∠BEC=∠CDB=90°
∴∠1+∠ACB=90°,∠2+∠ABC=90°(直角三角形两个锐角互余)
∴∠1=∠2(等角的余角相等)
∴BM=CM(等角对等边)例4:如图,在等边△ABC中,AF=BD=CE, 求证:△DEF也是等边三角形.证明:∵△ABC是等边三角形
∴AC=BC,∠A=∠C
∵CE=BD
∴BC-BD=AC-CE
∴CD=AE
在△AEF和△CDE中
∴△AEF≌△CDE(SAS)
∴EF=DE
同理可证EF=DF
∴EF=DE=DF
∴△DEF是等边三角形
有两边相等的三角形是等腰三角形三线合一是轴对称图形等角对等边课堂小结等边对等角推论(P133)
推论1、2(P137)定理(P137)
等腰三角形的性质一.基本概念 1.定义:两条边相等的三角形叫做等腰三角形. 如图AB=AC, 就是等腰三角形 2.等腰三角形的基本要素:操作: 现在请同学们将所画的等腰三角形对折,
使两腰 AB、AC重叠在一起,折痕为AD,
你能发现什么现象呢?二.等腰三角形性质的探索BACD 通过折叠你发现图形中有哪些相等的线段或角?(1)、等腰三角形是轴对称图形(2)、∠ B =∠ C,(3)、BD = CD,(4)、∠ADB = ∠ADC = 90°,(5)、∠BAD = ∠CAD ,由上述结论(2)可得如下性质:定理1 等腰三角形的两底角相等.简称“等边对等角”.由上述结论(3)、(4)、(5)可得如下性质:定理2 等腰三角形顶角的平分线垂直平分底边.(“三线合一”)归纳:即两底角相等即AD 为底边上的中线即AD为底边上的高即AD为顶角平分线CDBA1、(1) 在ΔABC中,∵AB=AC,
∴ ∠B=∠C( )等边对等角① ∵AD⊥BC,
∴∠____ = ∠____,___= ___ ② ∵AD是中线,∴___⊥___ ,∠____ =∠____③∵AD是角平分线,
∴___ ⊥___ ,___ =___BAD CADBD CD AD BC AD BCBAD CADBD CD(2) 在△ABC中, AB=AC时, 课堂练习:(三线合一)2 、在△ ABC中,若AB=BC=CA,
则 ∠A=______
∠B=______
∠C=______
推论:
等边三角形三个内角都相等,每一个角都等于 。课堂练习:60 °60 °60 °60°
解:∵ AB=AC(已知)
∴∠B=∠C(等边对等角)
∴∠B=∠C= 30°
又∵BD=AD(已知)
∴∠BAD=∠B= 30°(等边对等角)
同理 ∠CAE =∠C= 30°
∴∠DAE =∠BAC-∠BAD-∠CAE
=120°-30°-30°
=60 °例1: 如图在△ABC中,AB=AC,∠BAC=120°,点D、E是底边的两点,且BD=AD,CE=AE,
求∠DAE的度数。能力拓展: 已知,如图AB=AC,AD=AE。求证:BD=CE。EDCBA方法一:
证明: ∵AB=AC
∴∠B=∠C(等边对等角)
同理:∠ADE=∠AED
又∵ ∠ADE+∠ADB=180°
∠AED+∠AEC=180 °
∠ADB=∠AEC(等角的补角相等)
在△ABD与△ ACD中
∵ ∠B=∠C
∠ADB=∠AEC
AD=AE
∴ △ ABD≌ △ ACE(AAS)
∴ BD=CE方法二:
过A作AF⊥BC垂足为F点,
∵ AB=AC
∴BF=FC(三线合一)
同理:DF=EF
∴BF-DF=FC-EF
即BD=CEF∟方法三:
证明△ ABE≌ △ ACD拓展:如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。解:∵AB=AC,BC=AD=BD∴∠ABC=∠C=∠BDC
∠A=∠ABD (等边对等角)设∠A=x,则∠BDC=∠A+∠ABD=2X则∠ABC=∠C=∠BDC=2X 在△ABC中,有
∠A+∠ABC+∠C=X+2X+2X=1800解得 X=360在△ABC中,∠A=360,∠ABC=∠C=720⒈等腰三角形一个底角为40°,它的顶角为______.⒉等腰三角形一顶角为40°,它的另外两个底角为
__________________.⒊等腰三角形一个角为40°,它的另外两个角为___________.100 °100°,40 °
或70 °,70 ° 70°,70°4.等腰三角形一个角为120°,它的另外两个角为 . 30°30°巩固练习:5.如图,AD是△ABC的外角∠EAC的平分线,且AD∥BC,试判断△ABC的形状,并说明理由? BDACE12巩固练习:6.已知:如图,AD∥BC,BD平分∠ABC,试判断△ABD的形状,并说明理由?C巩固练习:7.如图,在等腰△ABC中,AB=AC,两底角的平分线BE和CD相交于点O,那么△OBC是什么三角形?为什么?ABCEDO巩固练习:8.如图,在△ABC中,已知∠ABC=∠ACB,BF平分∠ABC,CF平分∠ACB,EG∥BC.请想想看,由以上条件,你能推导出什么结论?并说明理由.ABCF巩固练习:9.如图,△ABC中,∠C=90°,AC=BC,AD是角平分线。求证:AB=AC+DC。ABCED巩固练习:10、如图,已知AB=AC,EB=EC,
结论∠ABE= ∠ACE是否正确?
说明理由。巩固练习:小结:1、等腰三角形的性质:等边对等角2、 等腰三角形顶角的平分线垂直平分底边(三线合一)本节课你学到了什么? 4、利用等腰三角形的“三线合一”性质作辅助线(顶角的平分线、底边上的高、底边上的中线),帮助我们解决实际问题。3、等边三角形三个内角相等,每一个内角都等于60°15.3 等腰三角形第2课时
等腰三角形的判定等腰三角形的性质?1.等腰三角形的两底角相等(简称“等边对等角”)
2.等腰三角形顶角的平分线、底边上的中线 和底边上的高互相重合(简称“三线合一”) 思考 :1、如图:ΔABC中,已知AB=AC,
∠ B= ∠ C(在同一个三角形中,
等边对等角).
2、反过来:在ΔABC中,∠ B= ∠ C,
AB=AC成立吗?
已知:ΔABC中,∠B=∠C求证:AB=AC证明:作∠BAC的平分线AD在ΔBAD和ΔCAD中,∠BAD=∠CAD,
∠B=∠C,
AD=AD∴ ΔBAD≌ ΔCAD(AAS)∴AB=AC已知在一个三角形中,等角对等边定理 有两个角相等的三角形是
等腰三角形.简称(“等角对等边”) 在△ABC中, ∵∠B=∠C ( ) ∴ AC=AB. ( )用符号语言表示为:这又是一个判定两条线段相等根据之一.
归纳:由上述定理我们可以得到什么启示:已知:如图,⊿ABC中, ∠ A=∠B=∠C
求证:AB=AC=BC
证明:在⊿ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理CA=AB
∴BC=CA=AB
推论1 三个角都相等的三角形是等边三角形。已知: ⊿ABC中,AB=AC, ∠ A=600。
求证:AB=AC=BC证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ A=600
∴ ∠B=∠C = 600
∴AB=AC=BC
已知: ⊿ABC中,AB=AC, ∠B=600。
求证:AB=AC=BC证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ B=600
∴ ∠C = 600
∴∠ A=600
∴AB=AC=BC
推论2 有一个角是600的等腰三角形是等边三角形。 如图:△ABC是直角三角形,其中,∠C=90°
∠A=30°,延长BC到点D,使BC=DC,则△ABD是等边三角形。则AB=BD=AD=1/2BC。 ABDC30°定理 在直角三角形中,
如果一个锐角等于30°,
那么它所对的直角边等
于斜边的一半。
问:如图,下列推理正确吗? (等角对等边)(等角对等边)错,因为都不是在同一个三角形中。练一练:解: ∵ ∠ DAC= ∠ ACB+ ∠ ABC
(三角形外角的性质)∴ ∠ ABC= ∠ DAC -∠ ACB
=60 °- 30 ° =30 °∵ ∠ ABC= ∠ ACB∴ AB=AC(在同一个三角形中, 等角对等边)即AC的长就是河宽。 范例讲解:例1:一次数学实践活动的内容是测量河宽,如图,即测量A, B之间的距离。小明想出了一个方法:从点A出发,沿着与直线AB成60 °角的AC方向前进至C , 在C处测得∠ C= 30 °,量出AC的长,它就是河的宽度。这个方法正确吗?请说明理由。想一想:还有其它测量河宽的方法吗?例2:已知,如图等边△AEB与等边△BCD在线段AC的同侧。 求证: △ABD≌△EBCA B C DE变式:已知如图△ABD与△ACE均为等边三角形,求证:DC=BE想一想:
你还能写出哪些结论
例3:如图,已知在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD与CE相交于M点。求证:BM=CM。证明:∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∴BD⊥AC于D,CE⊥AB于E
∴∠BEC=∠CDB=90°
∴∠1+∠ACB=90°,∠2+∠ABC=90°(直角三角形两个锐角互余)
∴∠1=∠2(等角的余角相等)
∴BM=CM(等角对等边)例4:如图,在等边△ABC中,AF=BD=CE, 求证:△DEF也是等边三角形.证明:∵△ABC是等边三角形
∴AC=BC,∠A=∠C
∵CE=BD
∴BC-BD=AC-CE
∴CD=AE
在△AEF和△CDE中
∴△AEF≌△CDE(SAS)
∴EF=DE
同理可证EF=DF
∴EF=DE=DF
∴△DEF是等边三角形
有两边相等的三角形是等腰三角形三线合一是轴对称图形等角对等边课堂小结等边对等角推论(P133)
推论1、2(P137)定理(P137)
