4.3.3 《余角和补角》 课件(共23张PPT)
文档属性
| 名称 | 4.3.3 《余角和补角》 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 15:19:03 | ||
图片预览






文档简介
(共23张PPT)
第四章 几何图形初步
4.3 角
4.3.3 余角和补角
主讲人:数学可以很简单
目录
课前导入
探索新知
巩固练习
课堂小结
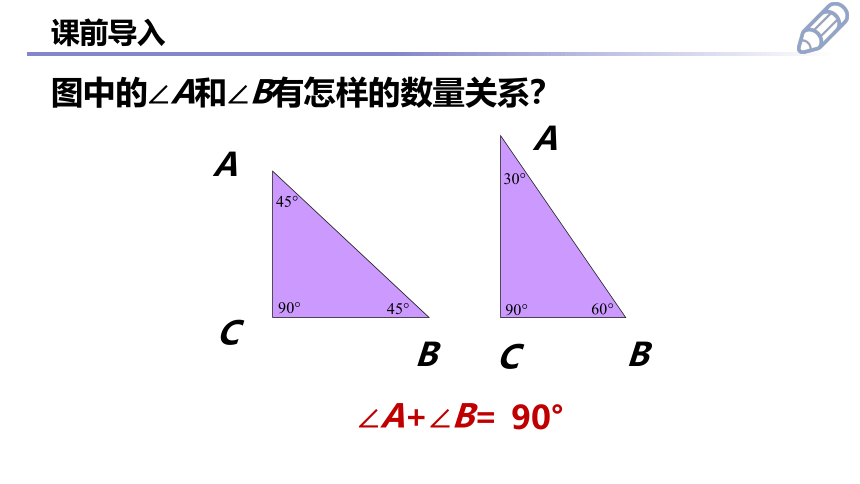
课前导入
A
C
B
A
C
B
∠A+∠B=
90°
图中的∠A和∠B有怎样的数量关系?
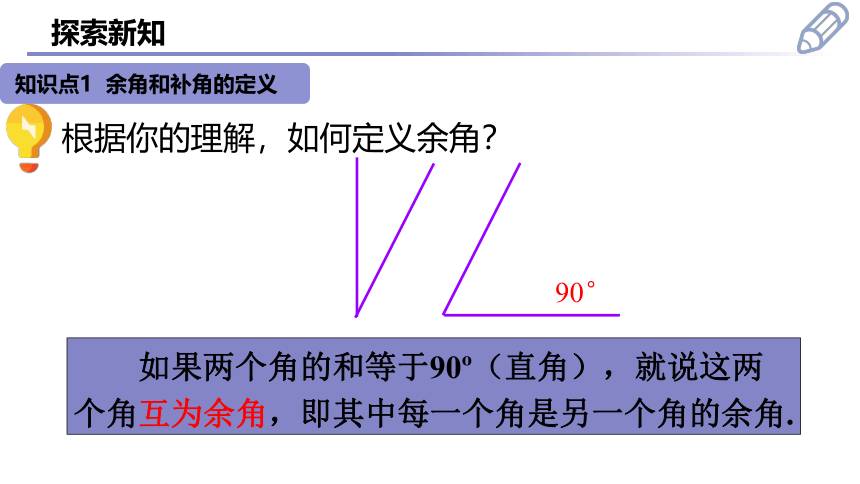
探索新知
知识点1 余角和补角的定义
根据你的理解,如何定义余角?
如果两个角的和等于90 (直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
90°
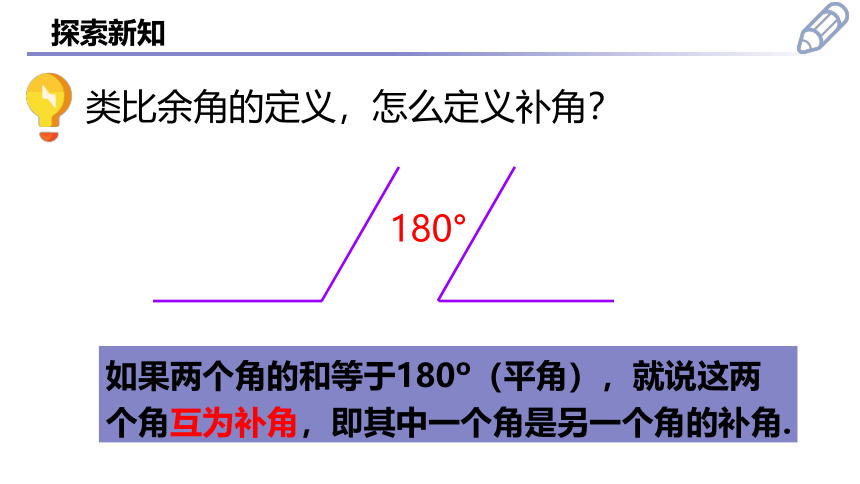
探索新知
类比余角的定义,怎么定义补角?
如果两个角的和等于180 (平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
180°
探索新知
∠1与∠2互为余角,∠1与∠3互为余角,那么∠2与∠3有怎样的数量关系呢?
你能证明这个结论吗?
∠2=∠3.
探索新知
已知:∠1与∠2互余,∠1与∠3互余,
求证:∠2=∠3.
证明:因为∠1与∠2互余,
所以∠1+∠2= ,
所以∠2= -∠1.
同理,因为∠1与∠3互余,
所以∠1+∠3= ,
所以∠3= -∠1.
由等式性质可得 ∠2=∠3.
同角的余角相等.
探索新知
如果∠1+∠2= ,∠3+∠4= ,且∠1=∠3,那么∠2=∠4吗?
因为∠1+∠2= ,∠3+∠4= ,
且∠1=∠3,
所以∠2=∠4.
等角的余角相等.
探索新知
如何证明?
如果∠1与∠2互补,∠3与∠4互补,且∠1=∠3,那么∠2=∠4吗?
∠2=∠4.
探索新知
证明:因为∠1与∠2互补,
所以∠1+∠2=180 ,
所以∠2=180 -∠1.
同理,因为∠3与∠4互补,
所以∠3+∠4=180 .
所以∠4=180 -∠3.
因为∠1=∠3,
所以∠2=∠4.
已知:∠1与∠2互补,∠3与∠4互补,且∠1=∠3,
求证:∠2=∠4.
等角的补角相等.
探索新知
如果∠1+∠2=180 ,∠1+∠3=180 ,那么∠2=∠3吗?
等角的补角相等.
∠2=∠3.
探索新知
同角(等角)的补角相等.
同角(等角)的余角相等.
探索新知
知识点1 余角和补角的应用
例1 如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC 和 ∠BOC,图中哪些角互为余角?
探索新知
分析:要找图中互余的角,就是要找和为 度的两个角.
90°
所以∠COD +∠COE
解:因为A,O,B在同一直线上,
所以∠AOC 和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC、∠BOC,
=90°
= (∠AOC+∠BOC)
探索新知
所以, ∠COD 和∠COE 互为余角,
同理, ∠AOD 和∠BOE,
∠AOD 和∠COE ,
∠COD 和∠BOE 也互为余角.
探索新知
例2 如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°、南偏西10°、西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
东
南
西
北
O
●
● A
60°
40°
B
C
10°
45°
D
巩固练习
巩固练习
练习2.一个角是70 39 ,求这个角的补角.
解: 互为补角的两个角和为180 ,
所以它的补角=180 -70 39
=109 21 .
答: 这个角的补角为109 21 .
巩固练习
练习3. ∠α的补角是它的3倍,∠α是多少度
巩固练习
练习4.一个角是钝角,它的一半是什么角?
课堂小结
余角和补角
如果两个角的和等于90 (直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
如果两个角的和等于180 (平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
性质:同角(等角)的余角相等.
同角(等角)的补角相等.
作业:
1. 完成习题4.3中第8,9题;
2.完成练习册本课时的习题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第四章 几何图形初步
4.3 角
4.3.3 余角和补角
主讲人:数学可以很简单
目录
课前导入
探索新知
巩固练习
课堂小结
课前导入
A
C
B
A
C
B
∠A+∠B=
90°
图中的∠A和∠B有怎样的数量关系?
探索新知
知识点1 余角和补角的定义
根据你的理解,如何定义余角?
如果两个角的和等于90 (直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
90°
探索新知
类比余角的定义,怎么定义补角?
如果两个角的和等于180 (平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
180°
探索新知
∠1与∠2互为余角,∠1与∠3互为余角,那么∠2与∠3有怎样的数量关系呢?
你能证明这个结论吗?
∠2=∠3.
探索新知
已知:∠1与∠2互余,∠1与∠3互余,
求证:∠2=∠3.
证明:因为∠1与∠2互余,
所以∠1+∠2= ,
所以∠2= -∠1.
同理,因为∠1与∠3互余,
所以∠1+∠3= ,
所以∠3= -∠1.
由等式性质可得 ∠2=∠3.
同角的余角相等.
探索新知
如果∠1+∠2= ,∠3+∠4= ,且∠1=∠3,那么∠2=∠4吗?
因为∠1+∠2= ,∠3+∠4= ,
且∠1=∠3,
所以∠2=∠4.
等角的余角相等.
探索新知
如何证明?
如果∠1与∠2互补,∠3与∠4互补,且∠1=∠3,那么∠2=∠4吗?
∠2=∠4.
探索新知
证明:因为∠1与∠2互补,
所以∠1+∠2=180 ,
所以∠2=180 -∠1.
同理,因为∠3与∠4互补,
所以∠3+∠4=180 .
所以∠4=180 -∠3.
因为∠1=∠3,
所以∠2=∠4.
已知:∠1与∠2互补,∠3与∠4互补,且∠1=∠3,
求证:∠2=∠4.
等角的补角相等.
探索新知
如果∠1+∠2=180 ,∠1+∠3=180 ,那么∠2=∠3吗?
等角的补角相等.
∠2=∠3.
探索新知
同角(等角)的补角相等.
同角(等角)的余角相等.
探索新知
知识点1 余角和补角的应用
例1 如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC 和 ∠BOC,图中哪些角互为余角?
探索新知
分析:要找图中互余的角,就是要找和为 度的两个角.
90°
所以∠COD +∠COE
解:因为A,O,B在同一直线上,
所以∠AOC 和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC、∠BOC,
=90°
= (∠AOC+∠BOC)
探索新知
所以, ∠COD 和∠COE 互为余角,
同理, ∠AOD 和∠BOE,
∠AOD 和∠COE ,
∠COD 和∠BOE 也互为余角.
探索新知
例2 如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°、南偏西10°、西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
东
南
西
北
O
●
● A
60°
40°
B
C
10°
45°
D
巩固练习
巩固练习
练习2.一个角是70 39 ,求这个角的补角.
解: 互为补角的两个角和为180 ,
所以它的补角=180 -70 39
=109 21 .
答: 这个角的补角为109 21 .
巩固练习
练习3. ∠α的补角是它的3倍,∠α是多少度
巩固练习
练习4.一个角是钝角,它的一半是什么角?
课堂小结
余角和补角
如果两个角的和等于90 (直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
如果两个角的和等于180 (平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
性质:同角(等角)的余角相等.
同角(等角)的补角相等.
作业:
1. 完成习题4.3中第8,9题;
2.完成练习册本课时的习题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
