数学人教A版(2019)必修第一册5.4.1正弦函数、余弦函数的图象(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.4.1正弦函数、余弦函数的图象(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 933.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 19:08:49 | ||
图片预览





文档简介
(共20张PPT)
生活中的正弦/余弦曲线
人教A版高中数学必修第一册
1.理解利用正弦函数的定义画正弦曲线的方法
2.能熟练掌握“五点法”作图的步骤
3.理解正弦函数图像与余弦函数图像之间的关系
5.4.1正弦函数、余弦函数的图像
探究.01
绘制正弦函数 y=sinx (x∈R) 的图象
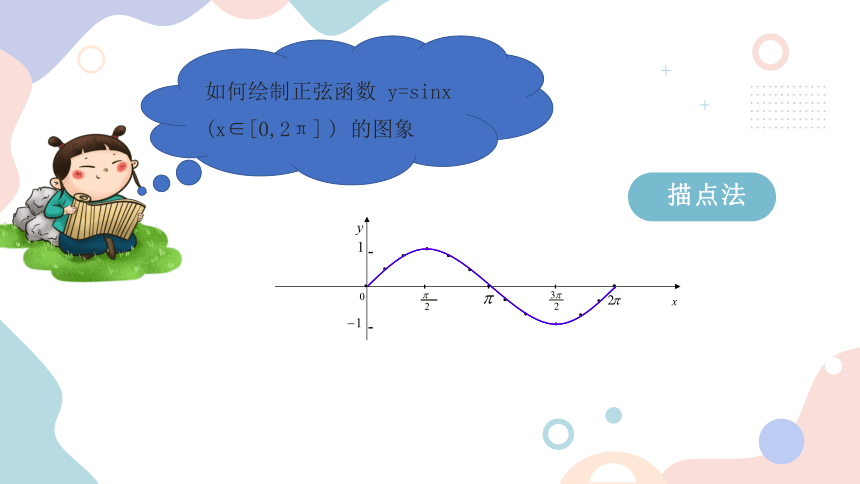
描点法
-
-
-
-
-
-
如何绘制正弦函数 y=sinx (x∈[0,2π] ) 的图象
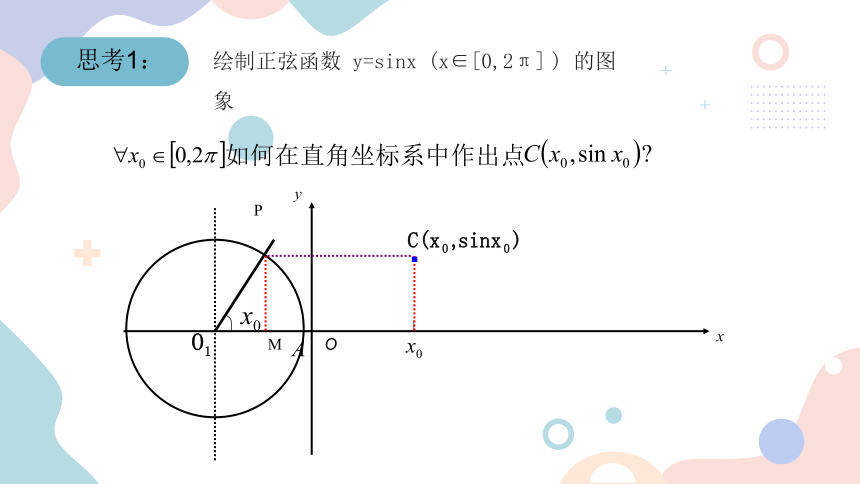
思考1:
绘制正弦函数 y=sinx (x∈[0,2π] ) 的图象
如何在直角坐标系中作出点
O
P
M
x
y
.
几何法
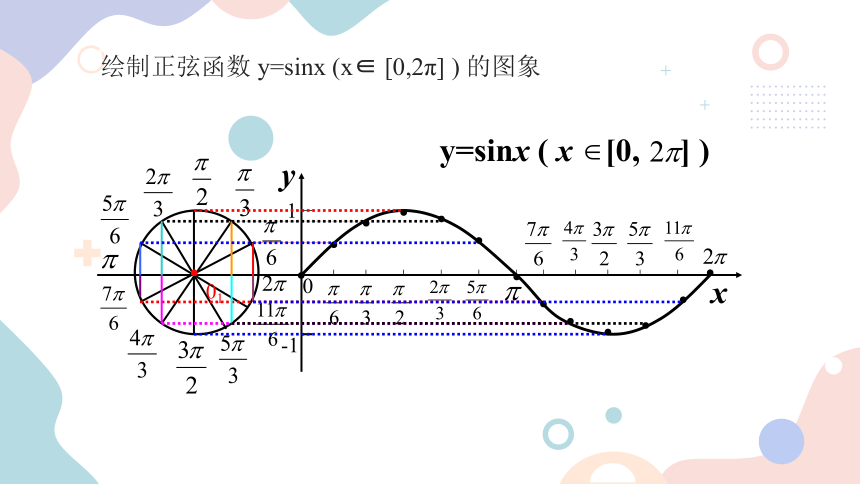
绘制正弦函数 y=sinx (x∈ [0,2π] ) 的图象
1
-1
0
y
x
●
●
●
y=sinx ( x [0, ] )
●
●
●
●
●
●
●
●
●
●
●
01
思考2:如何画出正弦函数y=sinx, x∈R的图象
y
x
o
正弦函数y=sinx, x R的图象叫正弦曲线.
y=sinx x [0,2 ]
y=sinx x R
sin(x+2k )=sinx, k Z
五点法
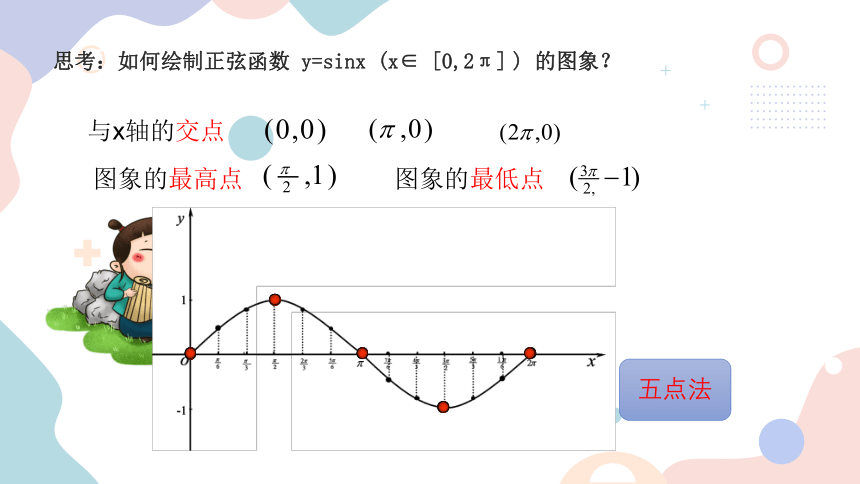
思考:如何绘制正弦函数 y=sinx (x∈ [0,2π] ) 的图象?
与x轴的交点
图象的最高点
图象的最低点
五点法
思考:你能根据诱导公式,以正弦函数的图像为基础,通过适当的图像变换得到余弦函数的图像吗?
小组合作
探究.02
绘制余弦函数 y=cosx (x∈R)的图象
正弦函数、余弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦函数的图象
正弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦曲线
正弦曲线
形状完全一样只是位置不同
1
-1
x
y
o
余弦函数的“五点画图法”
x
cosx
0
1
-1
0
1
与x轴的交点
图象的最高点
图象的最低点
与x轴的交点
图象的最高点
图象的最低点
五点作图法
x
y
o
例1.(1)作函数y=1+sinx,x∈[0,2π]的简图;
(2)作函数 y=-cosx, x∈[0, 2π]的简图.
解:(1)列表
用五点法描点做出简图
x
sinx
sinx+1
1
0
-1
0
0
1
2
1
1
0
函数y=1+sinx, x∈[0, 2π]与函数 y=sinx,x∈[0, 2π]的图象之间有何联系?
例1.(1)作函数y=1+sinx,x∈[0,2π]的简图;
(2)作函数 y=-cosx, x∈[0, 2π]的简图.
(1)按五个关键点列表
(2)用五点法做出简图
函数y=-cosx,与函数y=cosx, x∈[0,2π] 的图象有何联系?
x 0 π/2 π 3π/2 2π
cosx
-cosx
1
-1
0
1
-1
-1
0
0
1
0
O
x
1
-1
y
跟踪训练:画出下列函数的简图
(1)
(2)
课堂反馈
1.(多选)以下对正弦函数y=sin x的图象描述正确的是( )
A.在x∈[2kπ,2kπ+2π](k∈Z)上的图象形状相同,只是位置不同
B.介于直线y=1与直线y=-1之间
C.关于x轴对称
D.与y轴仅有一个交点
2.函数y=cos (-x),x∈[0,2π]的简图是( )
3.函数y=sin x,x∈[0,2π]的图象与直线y=的交点个数是()
A.1个 B.2个 C.3个 D.4个
1. 正弦曲线、余弦曲线作法
五点法(描点法)
图象变换法
y
x
o
1
-1
y=sinx,x [0, 2 ]
y=cosx,x [0, 2 ]
2.正弦曲线和余弦曲线之间的区别与联系;
课堂小结
一.知识与技能
二.数学思想方法
课堂作业
预习:
根据研究新函数的方法,通过图像探究正弦函数、余弦函数的性质
书面作业:
课本200页第1,2,3题
探究:
(1)余弦函数定义画余弦函数的图像;
(2)继续探索正弦函数、余弦函数的图像在生活中的具体应用.
会用数学眼光观察世界
会用数学思维思考世界
会用数学语言表达世界
生活中的正弦/余弦曲线
人教A版高中数学必修第一册
1.理解利用正弦函数的定义画正弦曲线的方法
2.能熟练掌握“五点法”作图的步骤
3.理解正弦函数图像与余弦函数图像之间的关系
5.4.1正弦函数、余弦函数的图像
探究.01
绘制正弦函数 y=sinx (x∈R) 的图象
描点法
-
-
-
-
-
-
如何绘制正弦函数 y=sinx (x∈[0,2π] ) 的图象
思考1:
绘制正弦函数 y=sinx (x∈[0,2π] ) 的图象
如何在直角坐标系中作出点
O
P
M
x
y
.
几何法
绘制正弦函数 y=sinx (x∈ [0,2π] ) 的图象
1
-1
0
y
x
●
●
●
y=sinx ( x [0, ] )
●
●
●
●
●
●
●
●
●
●
●
01
思考2:如何画出正弦函数y=sinx, x∈R的图象
y
x
o
正弦函数y=sinx, x R的图象叫正弦曲线.
y=sinx x [0,2 ]
y=sinx x R
sin(x+2k )=sinx, k Z
五点法
思考:如何绘制正弦函数 y=sinx (x∈ [0,2π] ) 的图象?
与x轴的交点
图象的最高点
图象的最低点
五点法
思考:你能根据诱导公式,以正弦函数的图像为基础,通过适当的图像变换得到余弦函数的图像吗?
小组合作
探究.02
绘制余弦函数 y=cosx (x∈R)的图象
正弦函数、余弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦函数的图象
正弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦曲线
正弦曲线
形状完全一样只是位置不同
1
-1
x
y
o
余弦函数的“五点画图法”
x
cosx
0
1
-1
0
1
与x轴的交点
图象的最高点
图象的最低点
与x轴的交点
图象的最高点
图象的最低点
五点作图法
x
y
o
例1.(1)作函数y=1+sinx,x∈[0,2π]的简图;
(2)作函数 y=-cosx, x∈[0, 2π]的简图.
解:(1)列表
用五点法描点做出简图
x
sinx
sinx+1
1
0
-1
0
0
1
2
1
1
0
函数y=1+sinx, x∈[0, 2π]与函数 y=sinx,x∈[0, 2π]的图象之间有何联系?
例1.(1)作函数y=1+sinx,x∈[0,2π]的简图;
(2)作函数 y=-cosx, x∈[0, 2π]的简图.
(1)按五个关键点列表
(2)用五点法做出简图
函数y=-cosx,与函数y=cosx, x∈[0,2π] 的图象有何联系?
x 0 π/2 π 3π/2 2π
cosx
-cosx
1
-1
0
1
-1
-1
0
0
1
0
O
x
1
-1
y
跟踪训练:画出下列函数的简图
(1)
(2)
课堂反馈
1.(多选)以下对正弦函数y=sin x的图象描述正确的是( )
A.在x∈[2kπ,2kπ+2π](k∈Z)上的图象形状相同,只是位置不同
B.介于直线y=1与直线y=-1之间
C.关于x轴对称
D.与y轴仅有一个交点
2.函数y=cos (-x),x∈[0,2π]的简图是( )
3.函数y=sin x,x∈[0,2π]的图象与直线y=的交点个数是()
A.1个 B.2个 C.3个 D.4个
1. 正弦曲线、余弦曲线作法
五点法(描点法)
图象变换法
y
x
o
1
-1
y=sinx,x [0, 2 ]
y=cosx,x [0, 2 ]
2.正弦曲线和余弦曲线之间的区别与联系;
课堂小结
一.知识与技能
二.数学思想方法
课堂作业
预习:
根据研究新函数的方法,通过图像探究正弦函数、余弦函数的性质
书面作业:
课本200页第1,2,3题
探究:
(1)余弦函数定义画余弦函数的图像;
(2)继续探索正弦函数、余弦函数的图像在生活中的具体应用.
会用数学眼光观察世界
会用数学思维思考世界
会用数学语言表达世界
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
