人教版(2019)物理必修第二册5.2运动的合成与分解 课件(共34张PPT)
文档属性
| 名称 | 人教版(2019)物理必修第二册5.2运动的合成与分解 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 957.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-21 14:55:39 | ||
图片预览










文档简介
(共34张PPT)
5.2 运动的合成与分解
1. 探究合运动与分运动的关系。
2. 利用平面直角坐标系定量研究蜡块运动的速度、位移和轨迹。
3. 探究合运动的性质和轨迹。
若人在河中始终保持头朝正前方游向对岸,你认为他会在对岸的正前方到达,还是会偏向上游或下游?为什么?
一、一个平面运动的实例
对类似上述的运动应该怎样分析呢?下面让我们从一个简单的平面运动开始研究。
想一想:
观察蜡块的运动
在一端封闭、长约 1 m 的玻璃管内注满清水,
水中放一个红蜡做的小圆柱体 A,将玻璃管的开
口端用橡胶塞塞紧(图 5.2-1 甲)。把玻璃管倒
置(图乙),蜡块 A 沿玻璃管上升。如果在玻璃
管旁边竖立一把刻度尺,可以看到,蜡块上升的速
度大致不变,即蜡块做匀速直线运动。 ①
在蜡块匀速上升的同时,将玻璃管紧贴着黑
板沿水平方向向右匀速移动(图丙),观察蜡块
的运动情况。
1.建立坐标系:研究物体运动时,坐标系的选取很重要。
(1)对于直线运动,应沿着直线建立直线坐标系。
(2)研究物体在平面内的运动时,可以选择平面直角坐标系。
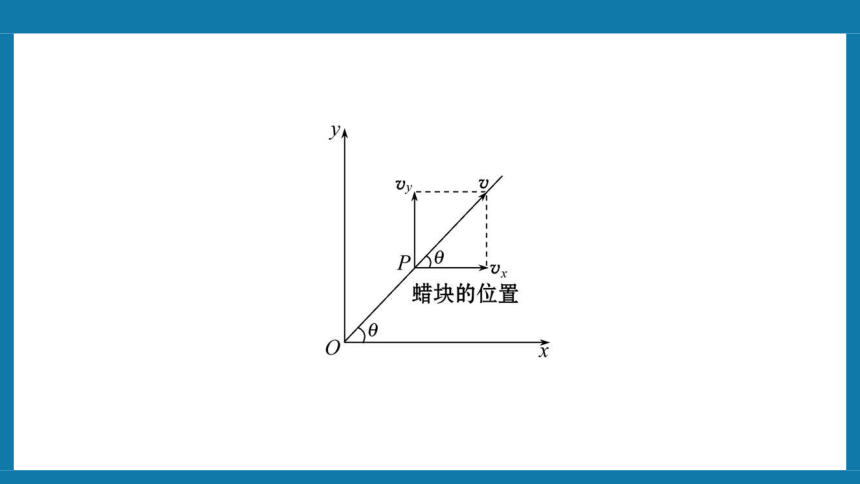
2.蜡块的运动轨迹:
(1)蜡块的位置:从蜡块开始运动的时刻计时,在t时刻,蜡块的位置P可以用它的x、y两个坐标表示:x=vxt,y=vyt。
(2)蜡块的速度:大小为,速度的方向满足tan =。
(3)蜡块的运动轨迹:y=x,是一条过原点的直线。
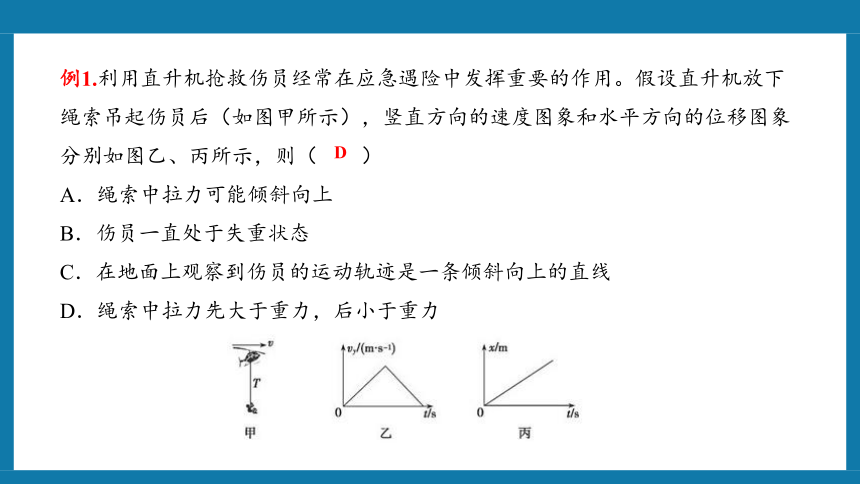
例1.利用直升机抢救伤员经常在应急遇险中发挥重要的作用。假设直升机放下绳索吊起伤员后(如图甲所示),竖直方向的速度图象和水平方向的位移图象分别如图乙、丙所示,则( )
A.绳索中拉力可能倾斜向上
B.伤员一直处于失重状态
C.在地面上观察到伤员的运动轨迹是一条倾斜向上的直线
D.绳索中拉力先大于重力,后小于重力
D
变式训练:
如图所示,一根长直轻杆AB在墙角沿竖直墙和水平地面滑动。当AB杆和墙的夹角为θ时,杆的A端沿墙下滑的速度大小为v1,B端沿地面滑动的速度大小为v2,则v1、v2的关系是( )
A.v1=v2
B.v1=v2cos θ
C.v1=v2tan θ
D.v1=v2sin θ
C
解析:如图所示,将杆的A端的速度沿杆的方向和垂直于杆的方向进行分解可得,沿杆方向的分速度为v1∥=v1cos θ,将杆的B端的速度沿杆的方向和垂直于杆的方向进行分解可得,沿杆方向的分速度v2∥=v2sin θ。由于v1∥=v2∥,解得v1=v2tan θ,故C正确。
故选:C
技法点拨:
根据竖直方向上加速度的方向判断出是否处于失重状态;根据水平方向运动的特点判断绳子沿水平方向的拉力;根据运动的合成的特点分析运动的轨迹;根据牛顿第二定律分析绳子上拉力的变化。结合v-t图象与x-t图象综合考查牛顿第二定律的应用以及运动的合成,涉及的知识点多,思维的密度相对比较大,在解答的过程中要缜密思考。
二、运动的合成与分解
1.内涵:
(1)合运动与分运动:如果物体同时参与了几个运动,那么物体实际发生的运动就是合运动,参与的几个运动就是分运动。
(2)运动的合成与分解:已知分运动求合运动,叫运动的合成;已知合运动求分运动,叫运动的分解。
2.运动的合成与分解的运算法则:合成与分解的内容是位移、速度、加速度的合成与分解,这些量都是矢量,遵循的是平行四边形定则。
3.合运动与分运动的关系:
等效性 各分运动的共同效果与合运动的效果相同
等时性 各分运动与合运动同时发生,同时结束,经历的时间相同
独立性 各分运动之间互不相干,彼此独立,互不影响
同体性 各分运动与合运动是同一物体的运动
X
Y
A
B
合运动和分运动具有等时性
V
vx
vy
合运动
水平分运动
竖直分运动
合速度?
分速度?
α
4.确定合运动性质的方法:
分析两个直线运动的合运动的性质时,应先根据平行四边形定则,确定合运动的合初速度v0和合加速度a,然后进行判断:
(1)判断是否做匀变速运动:若a恒定,物体做匀变速运动;若a变化,物体做变加速运动。
(2)判断轨迹曲直:若a与v0共线,则做直线运动;若a与v0不共线,则做曲线运动。
运动的合成与分解的应用
1.确定物体的合运动(实际发生的运动)与分运动。
2.画出矢量(速度、位移或加速度)合成或分解的平行四边形。
3.应用运动学公式分析同一运动(合运动或某一分运动)中的位移、速度、加速度等物理量之间的关系,应用几何知识分析合矢量与分矢量之间的关系。
小船渡河模型
(1)合运动与分运动:小船渡河时实际上参与了两个方向的分运动,即随水流的运动(水冲船的运动)和船在静水中的运动(运动方向为船头朝向的方向),船的实际运动是合运动。
甲 乙
(2)处理方法:
①根据运动的实际效果去分析;
②利用正交分解法去分析。
我们以渡河时间最短为例,讲解两种方法。
方法1:若使小船渡河的时间最短,那么船在实际运动时,应使船头正对河岸行驶,如图甲所示,此时渡河时间为t=(d为河宽),此时小船一定在对岸下游处靠岸。
方法2:将船相对水的速度沿平行于河岸和垂直于河岸方向正交分解,如图乙所示,则v水-v船cos θ为船实际沿水流方向的速度,v船sin θ为船垂直于河岸方向的速度。要使小船渡河时间最短,则应使v船sin θ最大,即当θ=90°(船头方向与河岸垂直)时,小船渡河时间最短,最短时间为 。
③小船渡河问题的常考模型
情况 图示 说明
渡河时 间最短 当船头垂直于河岸时,小船渡河时间最短,最短时间为= ,对应渡河位移x=
渡河位 移最短 当v水情况 图示 说明
渡河位 移最短 当v水>v船时,如果船头方向(v船方向)与合速度方向垂直,小船渡河位移最短,此时船头与河岸夹角为 ,最短渡河位移= =
渡河船 速最小 在水流速度v水和船的航行方向(v合方向)一定的前提下,当船头方向(v船方向)与合速度方向垂直时,有满足条件的最小船速,即
例2.下列说法中正确的是( )
A.处于“超重”现象的物体是因为该物体受到的重力增加了
B.甲、乙两队进行“拔河”比赛,若甲队获胜,则甲队拉绳的力一定大于乙队拉绳的力
C.牛顿第一定律是实验定律,可以用实验进行验证
D.两个初速度不为零的匀变速直线运动的合运动一定是匀变速运动
D
解析:A、物体处于超重状态,是对支撑面的压力增大,重力不变,故A错误;
B、甲、乙两队进行拔河比赛,甲队拉绳的力与乙队拉绳的力为作用力与反作用力,故B错误;
C、牛顿第一定律是牛顿在前人实验的基础上,根据逻辑推理得出的,不能用实验来验证,故C错误;
D、两个初速度不为零的匀变速直线运动,它们受到的都是恒力,所以它们的合运动受到的力也一定是恒力,加速度是恒定的,所以合运动一定是匀变速运动,故D正确;
故选:D。
变式训练:
如图所示,一个弯成半圆形的固定硬杆AB,一根绳子跨过B端的定滑轮后,连接一个套在杆上的小环。小环在绳子的拉动下从靠近A端开始沿着杆AB运动到B端,已知拉绳速度恒为v,则小环从A到B的运动情况是( )
A.越来越快
B.越来越慢
C.先变快后变慢
D.先变慢后变快
B
技法点拨:
(1)当物体对接触面的压力大于物体的真实重力时,就说物体处于超重状态,此时有向上的加速度;
(2)由牛顿第三定律可知,作用力与反作用力大小相等,方向相反,作用在同一条直线上,作用在两个物体上;
(3)牛顿第一定律是牛顿在前人实验的基础上,根据逻辑推理得出的,是以实验为基础,但又不是完全通过实验得出;
(4)根据力的矢量叠加原理可知两个恒力的合力也为恒力,受到合力作用的物体一定是匀变速运动。
分运动
合运动
运动的合成
运动的分解
分速度
分位移
分加速度
合速度
合位移
合加速度
遵循平行四边形定则
等时性
等效性
独立性
1.关于合运动与分运动,下列说法正确的是 ( )
A.合运动的速度等于两个分运动的速度之和
B.合运动的时间一定等于分运动的时间
C.两个直线运动的合运动一定是直线运动
D.合运动的速度方向一定与其中某一分速度方向相同
解析:选B。根据平行四边形定则知,合运动的速度可能比分运动的速度大,可能比分运动的速度小,可能与分运动的速度相等,故A错误;合运动与分运动具有等时性,故B正确;两个直线运动的合运动不一定是直线运动,故C错误;合运动的速度方向可以与某一分运动的速度方向相同,也可能不同,故D错误。
B
2.关于运动的性质,以下说法中正确的是 ( )
A.曲线运动一定是变速运动
B.变速运动一定是曲线运动
C.加速度大小和速度大小都不变的运动一定是直线运动
D.只要两个分运动是直线运动,则合运动一定是直线运动
解析:选A。无论是物体速度的大小变了,还是速度的方向变了,都说明速度是变化的,都是变速运动,做曲线运动的物体的速度方向在时刻改变,所以曲线运动一定是变速运动,故A正确;变速运动也可以是平时所学的匀加速直线运动或匀减速直线运动,并不一定是曲线运动,故B错误;加速度大小和速度大小都不变的运动不一定是直线运动,可能是曲线运动,故C错误;两个分运动是直线运动,则合运动不一定是直线运动,故D错误。
A
3.如图所示,帆船船头指向正东以速度v(静水中速度)航行,海面正刮着南风,风速为v,以海岸为参考系,不计阻力。关于帆船的实际航行方向和速度大小,下列说法中正确的是 ( )
A.帆船北偏东30°方向航行,速度大小为2v
B.帆船东偏北60°方向航行,速度大小为v
C.帆船东偏北30°方向航行,速度大小为2v
D.帆船东偏南60°方向航行,速度大小为v
解析:选A。由于帆船的船头指向正东,并以相对静水中的速度v航行,南风以v的风速向北吹来,当以海岸为参考系时,实际速度v实==2v,设帆船实际航行方向与正北方向夹角为α,则sinα==,α=30°,即帆船沿北偏东30°方向航行,故A正确。
A
4.如图甲所示,竖直放置、两端封闭的玻璃管中注满清水,内有一个能在水中以0.3 m/s的速度匀速上浮的红蜡块。若红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动的方向与水平方向的夹角为37°,则:(sin 37°=0.6,cos 37°=0.8)
(1)根据题意可知玻璃管水平方向的移动速度为 m/s。
(2)如图乙所示,若红蜡块从A点匀速上浮的同时,使玻璃管水平向右做匀加速直线运动,则红蜡块实际运动的轨迹是图中的 。
A.直线P B.曲线Q C.曲线R D.无法确定
0.4
B
解析:(1)据平行四边形定则可知,玻璃管水平方向的移动速度为= =m/s=0.4m/s。
(2)红蜡块在竖直方向做匀速运动,在水平方向做匀加速直线运动,则红蜡块所受的合力方向水平向右,合速度方向与合力方向不共线,红蜡块做曲线运动;因为合力的方向指向轨迹的凹侧,可知红蜡块实际运动的轨迹是图中的曲线Q。
再见
5.2 运动的合成与分解
1. 探究合运动与分运动的关系。
2. 利用平面直角坐标系定量研究蜡块运动的速度、位移和轨迹。
3. 探究合运动的性质和轨迹。
若人在河中始终保持头朝正前方游向对岸,你认为他会在对岸的正前方到达,还是会偏向上游或下游?为什么?
一、一个平面运动的实例
对类似上述的运动应该怎样分析呢?下面让我们从一个简单的平面运动开始研究。
想一想:
观察蜡块的运动
在一端封闭、长约 1 m 的玻璃管内注满清水,
水中放一个红蜡做的小圆柱体 A,将玻璃管的开
口端用橡胶塞塞紧(图 5.2-1 甲)。把玻璃管倒
置(图乙),蜡块 A 沿玻璃管上升。如果在玻璃
管旁边竖立一把刻度尺,可以看到,蜡块上升的速
度大致不变,即蜡块做匀速直线运动。 ①
在蜡块匀速上升的同时,将玻璃管紧贴着黑
板沿水平方向向右匀速移动(图丙),观察蜡块
的运动情况。
1.建立坐标系:研究物体运动时,坐标系的选取很重要。
(1)对于直线运动,应沿着直线建立直线坐标系。
(2)研究物体在平面内的运动时,可以选择平面直角坐标系。
2.蜡块的运动轨迹:
(1)蜡块的位置:从蜡块开始运动的时刻计时,在t时刻,蜡块的位置P可以用它的x、y两个坐标表示:x=vxt,y=vyt。
(2)蜡块的速度:大小为,速度的方向满足tan =。
(3)蜡块的运动轨迹:y=x,是一条过原点的直线。
例1.利用直升机抢救伤员经常在应急遇险中发挥重要的作用。假设直升机放下绳索吊起伤员后(如图甲所示),竖直方向的速度图象和水平方向的位移图象分别如图乙、丙所示,则( )
A.绳索中拉力可能倾斜向上
B.伤员一直处于失重状态
C.在地面上观察到伤员的运动轨迹是一条倾斜向上的直线
D.绳索中拉力先大于重力,后小于重力
D
变式训练:
如图所示,一根长直轻杆AB在墙角沿竖直墙和水平地面滑动。当AB杆和墙的夹角为θ时,杆的A端沿墙下滑的速度大小为v1,B端沿地面滑动的速度大小为v2,则v1、v2的关系是( )
A.v1=v2
B.v1=v2cos θ
C.v1=v2tan θ
D.v1=v2sin θ
C
解析:如图所示,将杆的A端的速度沿杆的方向和垂直于杆的方向进行分解可得,沿杆方向的分速度为v1∥=v1cos θ,将杆的B端的速度沿杆的方向和垂直于杆的方向进行分解可得,沿杆方向的分速度v2∥=v2sin θ。由于v1∥=v2∥,解得v1=v2tan θ,故C正确。
故选:C
技法点拨:
根据竖直方向上加速度的方向判断出是否处于失重状态;根据水平方向运动的特点判断绳子沿水平方向的拉力;根据运动的合成的特点分析运动的轨迹;根据牛顿第二定律分析绳子上拉力的变化。结合v-t图象与x-t图象综合考查牛顿第二定律的应用以及运动的合成,涉及的知识点多,思维的密度相对比较大,在解答的过程中要缜密思考。
二、运动的合成与分解
1.内涵:
(1)合运动与分运动:如果物体同时参与了几个运动,那么物体实际发生的运动就是合运动,参与的几个运动就是分运动。
(2)运动的合成与分解:已知分运动求合运动,叫运动的合成;已知合运动求分运动,叫运动的分解。
2.运动的合成与分解的运算法则:合成与分解的内容是位移、速度、加速度的合成与分解,这些量都是矢量,遵循的是平行四边形定则。
3.合运动与分运动的关系:
等效性 各分运动的共同效果与合运动的效果相同
等时性 各分运动与合运动同时发生,同时结束,经历的时间相同
独立性 各分运动之间互不相干,彼此独立,互不影响
同体性 各分运动与合运动是同一物体的运动
X
Y
A
B
合运动和分运动具有等时性
V
vx
vy
合运动
水平分运动
竖直分运动
合速度?
分速度?
α
4.确定合运动性质的方法:
分析两个直线运动的合运动的性质时,应先根据平行四边形定则,确定合运动的合初速度v0和合加速度a,然后进行判断:
(1)判断是否做匀变速运动:若a恒定,物体做匀变速运动;若a变化,物体做变加速运动。
(2)判断轨迹曲直:若a与v0共线,则做直线运动;若a与v0不共线,则做曲线运动。
运动的合成与分解的应用
1.确定物体的合运动(实际发生的运动)与分运动。
2.画出矢量(速度、位移或加速度)合成或分解的平行四边形。
3.应用运动学公式分析同一运动(合运动或某一分运动)中的位移、速度、加速度等物理量之间的关系,应用几何知识分析合矢量与分矢量之间的关系。
小船渡河模型
(1)合运动与分运动:小船渡河时实际上参与了两个方向的分运动,即随水流的运动(水冲船的运动)和船在静水中的运动(运动方向为船头朝向的方向),船的实际运动是合运动。
甲 乙
(2)处理方法:
①根据运动的实际效果去分析;
②利用正交分解法去分析。
我们以渡河时间最短为例,讲解两种方法。
方法1:若使小船渡河的时间最短,那么船在实际运动时,应使船头正对河岸行驶,如图甲所示,此时渡河时间为t=(d为河宽),此时小船一定在对岸下游处靠岸。
方法2:将船相对水的速度沿平行于河岸和垂直于河岸方向正交分解,如图乙所示,则v水-v船cos θ为船实际沿水流方向的速度,v船sin θ为船垂直于河岸方向的速度。要使小船渡河时间最短,则应使v船sin θ最大,即当θ=90°(船头方向与河岸垂直)时,小船渡河时间最短,最短时间为 。
③小船渡河问题的常考模型
情况 图示 说明
渡河时 间最短 当船头垂直于河岸时,小船渡河时间最短,最短时间为= ,对应渡河位移x=
渡河位 移最短 当v水
渡河位 移最短 当v水>v船时,如果船头方向(v船方向)与合速度方向垂直,小船渡河位移最短,此时船头与河岸夹角为 ,最短渡河位移= =
渡河船 速最小 在水流速度v水和船的航行方向(v合方向)一定的前提下,当船头方向(v船方向)与合速度方向垂直时,有满足条件的最小船速,即
例2.下列说法中正确的是( )
A.处于“超重”现象的物体是因为该物体受到的重力增加了
B.甲、乙两队进行“拔河”比赛,若甲队获胜,则甲队拉绳的力一定大于乙队拉绳的力
C.牛顿第一定律是实验定律,可以用实验进行验证
D.两个初速度不为零的匀变速直线运动的合运动一定是匀变速运动
D
解析:A、物体处于超重状态,是对支撑面的压力增大,重力不变,故A错误;
B、甲、乙两队进行拔河比赛,甲队拉绳的力与乙队拉绳的力为作用力与反作用力,故B错误;
C、牛顿第一定律是牛顿在前人实验的基础上,根据逻辑推理得出的,不能用实验来验证,故C错误;
D、两个初速度不为零的匀变速直线运动,它们受到的都是恒力,所以它们的合运动受到的力也一定是恒力,加速度是恒定的,所以合运动一定是匀变速运动,故D正确;
故选:D。
变式训练:
如图所示,一个弯成半圆形的固定硬杆AB,一根绳子跨过B端的定滑轮后,连接一个套在杆上的小环。小环在绳子的拉动下从靠近A端开始沿着杆AB运动到B端,已知拉绳速度恒为v,则小环从A到B的运动情况是( )
A.越来越快
B.越来越慢
C.先变快后变慢
D.先变慢后变快
B
技法点拨:
(1)当物体对接触面的压力大于物体的真实重力时,就说物体处于超重状态,此时有向上的加速度;
(2)由牛顿第三定律可知,作用力与反作用力大小相等,方向相反,作用在同一条直线上,作用在两个物体上;
(3)牛顿第一定律是牛顿在前人实验的基础上,根据逻辑推理得出的,是以实验为基础,但又不是完全通过实验得出;
(4)根据力的矢量叠加原理可知两个恒力的合力也为恒力,受到合力作用的物体一定是匀变速运动。
分运动
合运动
运动的合成
运动的分解
分速度
分位移
分加速度
合速度
合位移
合加速度
遵循平行四边形定则
等时性
等效性
独立性
1.关于合运动与分运动,下列说法正确的是 ( )
A.合运动的速度等于两个分运动的速度之和
B.合运动的时间一定等于分运动的时间
C.两个直线运动的合运动一定是直线运动
D.合运动的速度方向一定与其中某一分速度方向相同
解析:选B。根据平行四边形定则知,合运动的速度可能比分运动的速度大,可能比分运动的速度小,可能与分运动的速度相等,故A错误;合运动与分运动具有等时性,故B正确;两个直线运动的合运动不一定是直线运动,故C错误;合运动的速度方向可以与某一分运动的速度方向相同,也可能不同,故D错误。
B
2.关于运动的性质,以下说法中正确的是 ( )
A.曲线运动一定是变速运动
B.变速运动一定是曲线运动
C.加速度大小和速度大小都不变的运动一定是直线运动
D.只要两个分运动是直线运动,则合运动一定是直线运动
解析:选A。无论是物体速度的大小变了,还是速度的方向变了,都说明速度是变化的,都是变速运动,做曲线运动的物体的速度方向在时刻改变,所以曲线运动一定是变速运动,故A正确;变速运动也可以是平时所学的匀加速直线运动或匀减速直线运动,并不一定是曲线运动,故B错误;加速度大小和速度大小都不变的运动不一定是直线运动,可能是曲线运动,故C错误;两个分运动是直线运动,则合运动不一定是直线运动,故D错误。
A
3.如图所示,帆船船头指向正东以速度v(静水中速度)航行,海面正刮着南风,风速为v,以海岸为参考系,不计阻力。关于帆船的实际航行方向和速度大小,下列说法中正确的是 ( )
A.帆船北偏东30°方向航行,速度大小为2v
B.帆船东偏北60°方向航行,速度大小为v
C.帆船东偏北30°方向航行,速度大小为2v
D.帆船东偏南60°方向航行,速度大小为v
解析:选A。由于帆船的船头指向正东,并以相对静水中的速度v航行,南风以v的风速向北吹来,当以海岸为参考系时,实际速度v实==2v,设帆船实际航行方向与正北方向夹角为α,则sinα==,α=30°,即帆船沿北偏东30°方向航行,故A正确。
A
4.如图甲所示,竖直放置、两端封闭的玻璃管中注满清水,内有一个能在水中以0.3 m/s的速度匀速上浮的红蜡块。若红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动的方向与水平方向的夹角为37°,则:(sin 37°=0.6,cos 37°=0.8)
(1)根据题意可知玻璃管水平方向的移动速度为 m/s。
(2)如图乙所示,若红蜡块从A点匀速上浮的同时,使玻璃管水平向右做匀加速直线运动,则红蜡块实际运动的轨迹是图中的 。
A.直线P B.曲线Q C.曲线R D.无法确定
0.4
B
解析:(1)据平行四边形定则可知,玻璃管水平方向的移动速度为= =m/s=0.4m/s。
(2)红蜡块在竖直方向做匀速运动,在水平方向做匀加速直线运动,则红蜡块所受的合力方向水平向右,合速度方向与合力方向不共线,红蜡块做曲线运动;因为合力的方向指向轨迹的凹侧,可知红蜡块实际运动的轨迹是图中的曲线Q。
再见
