第十二章全等三角形学案
图片预览


文档简介
第十二章 全等三角形
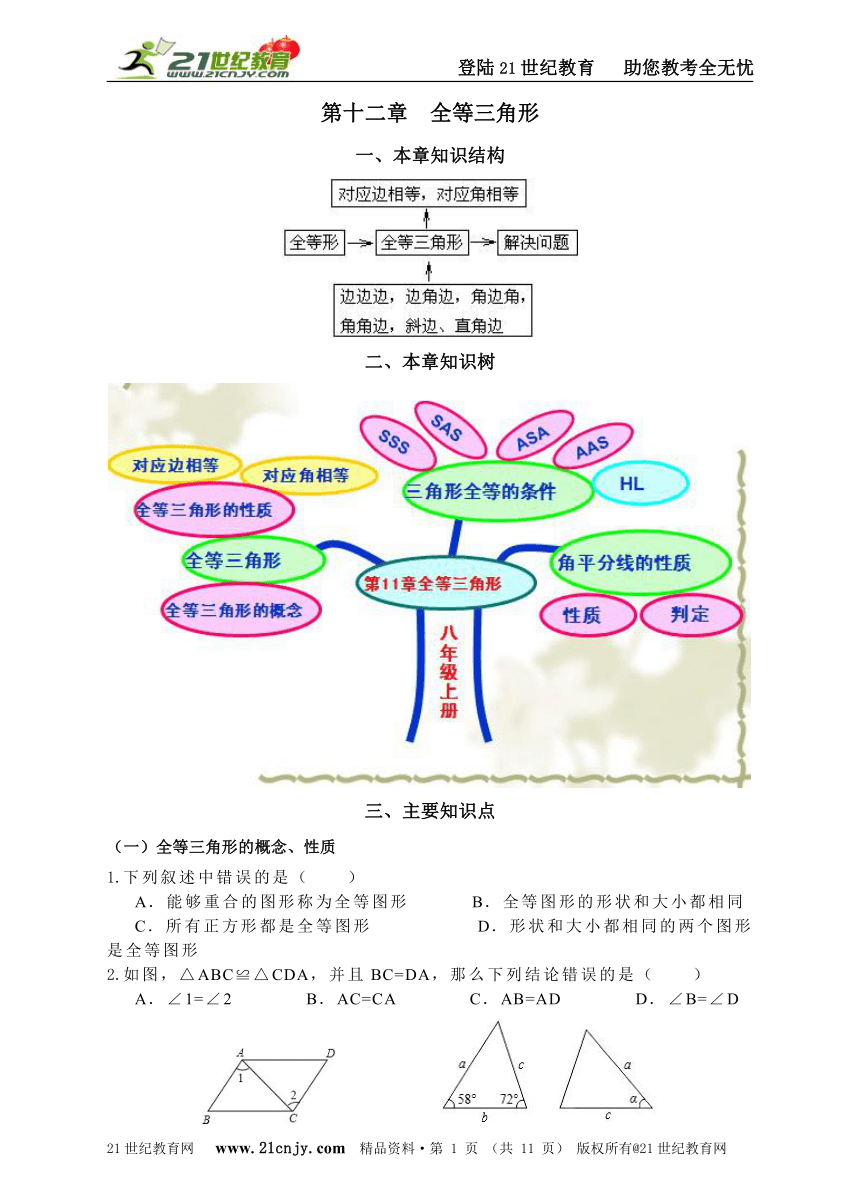
一、本章知识结构
二、本章知识树
三、主要知识点
(一)全等三角形的概念、性质
1.下列叙述中错误的是( )
A.能够重合的图形称为全等图形 B.全等图形的形状和大小都相同
C.所有正方形都是全等图形 D.形状和大小都相同的两个图形是全等图形
2.如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是( )
A.∠1=∠2 B.AC=CA C.AB=AD D.∠B=∠D
第2题 第3题
3.已知图中的两个三角形全等,则∠α的度数是 °.
4.如图,已知△ABC≌△ADE,若∠ABC=70°,∠DAE=80°,则∠C的度数是
°.
第4题 第5题
5.如图,已知△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,则∠EGF=
°.
【知识点】
1. 叫全等形, 叫全等三角形;
2.全等三角形性质:全等三角形的 相等, 相等, 相等, 相等,对应边上的 相等,对应角的 相等.
(二)全等三角形的判定
1. 如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
第1题 第2题 第3题 第4题
2. 尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,作射线OP.则射线OP就是∠AOB的平分线.由作法得△OCP≌△ODP的根据是 .
3. 如图,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是 .
4. 如图,在△ABC中AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是 .
5. 如图,在方格纸中的三个顶点及A、B、C、D、E五个点都在小方格的顶点上.现以A、B、C、D、E中的三个点为顶点画三角形.
(1)在图甲中画出一个三角形与△PQR全等;
(2)在图乙中画出一个三角形与△PQR面积相等但不全等.
第5题 第6题
6. 如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是 .
【知识点】
三角形全等的判定方法有 、 、 、 、 .
常见的全等变换有 、 、 .
(三)全等三角形的证明
1.如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E,求证:BC=DC.
如图,点E、F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.求证:AF=DC.
如图,C是AB的中点,AD=BE,CD=CE.求证:∠A=∠B.
如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.求证:AE=BC.
6.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.线段BD、CE有怎样的数量关系和位置关系?写出你猜想的结论并加以证明.
如图,两根旗杆AC,BD相距10米,旗杆AC高3米,且AC⊥AB,BD⊥AB,一同学从B点出发向A点走去,当他走到点M时,发现自己刚好走了3米,此时他仰望旗杆的顶点C,D,又发现两条视线CM=DM. (1)求旗杆BD的高为多少米? (2)两条视线CM,DM有怎样的位置关系?请说明理由.
8. 已知:如图,∠1=∠2,∠D+∠C=180°.求证:AC=BD.
(四)角平分线的性质
1. 如图,△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,BD=5cm,则D点到AB的距离是 cm.
第1题 第2题 第3题 第4题
2. 如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是 .
3. 如图,∠AOB=30°,OP平分∠AOB,PC∥OB,PD⊥OB,如果PC=6,那么PD等于 .
4. 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于E,若△DEB的周长为10cm,则AB的长为 cm.
5. 如图,△ABO中,AD⊥OB于D,BC⊥OA于C,AD,BC交于点E,且OE平∠AOB,求证:AE=BE.
6.如图,△ABC的角平分线AD、BE相交于点P, (1)在图1中,分别画出点P到边AC、BC、BA的垂线段PF、PG、PH,这3条线段相等吗?为什么? (2)在图2中,∠ABC是直角,∠C=60°,其余条件都不变,请你判断并写出PE与PD之间的数量关系,并说明理由.
7.如图,已知∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上移动,两直角边分别与边OA,OB交于点C,D.求证:PC=PD.
8.如图,在四边形ABCD中,已知∠1=∠2,∠A+∠C=180°.求证:AD=CD.
9.如图,已知:Rt△ABC中,∠C=90°,AC=BC,AD是∠A的平分线.求证:AC+CD=AB.
【知识点】
角平分线的性质: ;
角平分线的判定: .
已知角平分线时,常用的辅助线是: ; .
四、检测
一、选择题:
1. 如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠AEC等于( )
A.60° B. 50° C. 45° D. 30°
第1题 第2题 第3题 第4题
如图,直线l过等腰直角△ABC顶点B,A、C两点到直线l的距离分别是2和3,则MN的长是( )
A.5 B. 4 C. 3 D. 2
如图,AC⊥BE,∠A=∠E,不能判断△ABC≌△EDC的条件是( )
A.BC=DC B.∠B=∠CDE C.AB=DE D.AC=CE
如图,折叠直角△ABC,使点C落在AB上的点E处.已知BC=12,∠B=30°,则DE的长是( )
A.6 B. 4 C. 3 D. 2
二、填空题:
5.如图,△ABC≌△DBF,∠ABD=30°,则∠CBF的度数为 °.
第5题 第6题 第7题
6.如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有 (填序号).
7.如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件 ,使得△EAB≌△BCD.
8.如图,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE= cm.
第8题 第9题 第10题
9.如图,在Rt△ABC中,∠C=90°,∠B=60°,∠A的平分线AD交BC于D,则= .
10.如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是 .
三、解答题:
11.如图:已知D、E分别在AB、AC上,AB=AC,∠B=∠C,求证:BE=CD.
12.已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点.求证:BD=AE.
13.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.直线BF垂直于直线CE于点F,交CD于点G,求证:AE=CG.
14.已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上. (1)如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之; (2)如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
检测答案
A 2. A 3. B 4. B 5. 30
①③④ 7. 答案不惟一,如BE=BD,AE=BC等 8.7 9. 10. 21
11.证明:在△ACD和△ABE中,
∴△ACD≌△AEB(ASA), ∴BE=CD.
12.证明:∵△ABC和△ECD都是等腰直角三角形, ∴AC=BC,CD=CE, ∵∠ACB=∠DCE=90°, ∴∠ACE+∠ACD=∠BCD+∠ACD, ∴∠ACE=∠BCD, 在△ACE和△BCD中,
∴△ACE≌△BCD(SAS), ∴BD=AE.
证明:∵AC=BC,∠ACB=90°,点D是AB的中点,
∴∠A=∠BCD=45°,∠ACE+∠BCF=90°,
∵BF⊥CE,
∴∠CBGE+∠BCF=90°,
∴∠ACE=∠CBG.
在△ACE和△BCG中,
∴△ACE≌△BCG(ASA), ∴AE=CG.
解:(1)关系是:AD+AB=AC 证明:∵AC平分∠MAN,∠MAN=120° ∴∠CAD=∠CAB=60° 又∠ADC=∠ABC=90°, ∴∠ACD=∠ACB=30° 则AD=AB=AC ∴AD+AB=AC; (2)仍成立.
证明:过点C分别作AM、AN的垂线,垂足分别为E、F, ∵AC平分∠MAN ∴CE=CF, ∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180° ∴∠CDE=∠ABC 又∠CED=∠CFB=90°,∴△CED≌△CFB(AAS), ∵ED=FB,∴AD+AB=AE-ED+AF+FB=AE+AF, 由(1)知AE+AF=AC, ∴AD+AB=AC.
一、本章知识结构
二、本章知识树
三、主要知识点
(一)全等三角形的概念、性质
1.下列叙述中错误的是( )
A.能够重合的图形称为全等图形 B.全等图形的形状和大小都相同
C.所有正方形都是全等图形 D.形状和大小都相同的两个图形是全等图形
2.如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是( )
A.∠1=∠2 B.AC=CA C.AB=AD D.∠B=∠D
第2题 第3题
3.已知图中的两个三角形全等,则∠α的度数是 °.
4.如图,已知△ABC≌△ADE,若∠ABC=70°,∠DAE=80°,则∠C的度数是
°.
第4题 第5题
5.如图,已知△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,则∠EGF=
°.
【知识点】
1. 叫全等形, 叫全等三角形;
2.全等三角形性质:全等三角形的 相等, 相等, 相等, 相等,对应边上的 相等,对应角的 相等.
(二)全等三角形的判定
1. 如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
第1题 第2题 第3题 第4题
2. 尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,作射线OP.则射线OP就是∠AOB的平分线.由作法得△OCP≌△ODP的根据是 .
3. 如图,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是 .
4. 如图,在△ABC中AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是 .
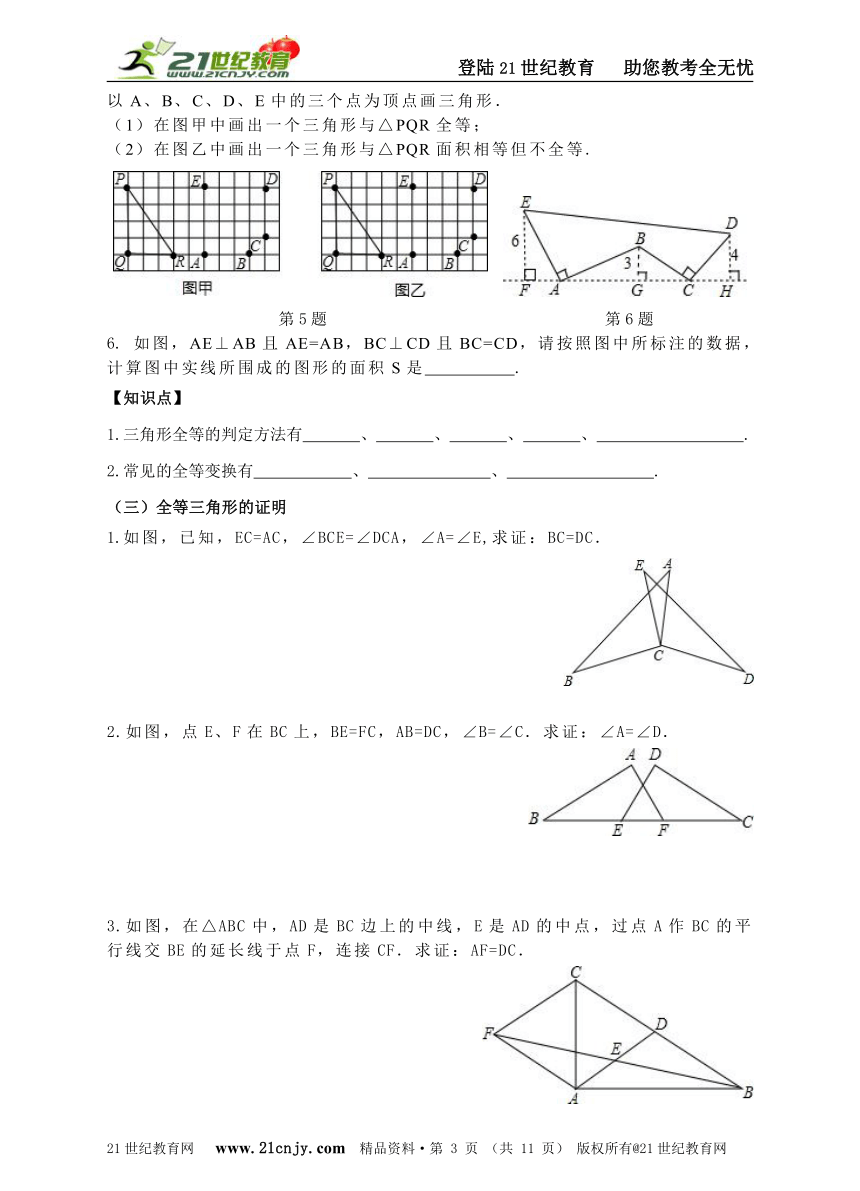
5. 如图,在方格纸中的三个顶点及A、B、C、D、E五个点都在小方格的顶点上.现以A、B、C、D、E中的三个点为顶点画三角形.
(1)在图甲中画出一个三角形与△PQR全等;
(2)在图乙中画出一个三角形与△PQR面积相等但不全等.
第5题 第6题
6. 如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是 .
【知识点】
三角形全等的判定方法有 、 、 、 、 .
常见的全等变换有 、 、 .
(三)全等三角形的证明
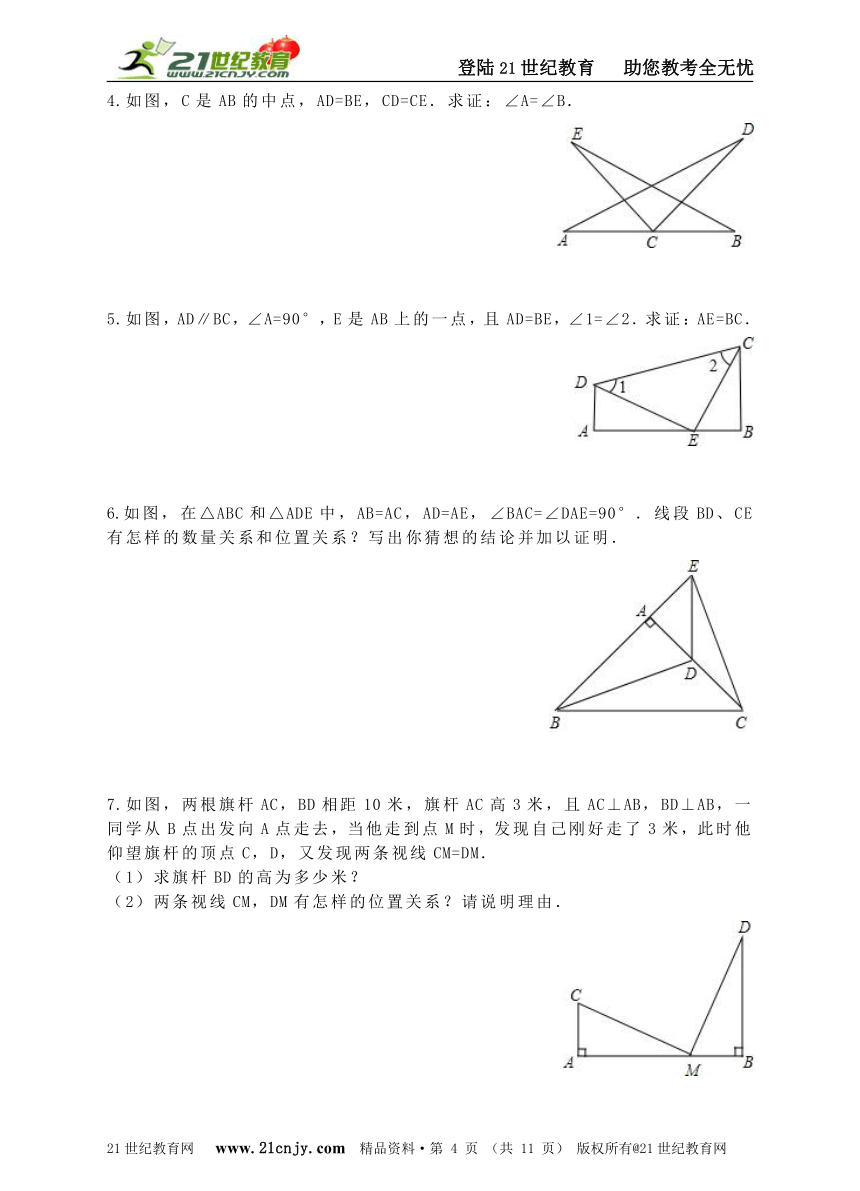
1.如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E,求证:BC=DC.
如图,点E、F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.求证:AF=DC.
如图,C是AB的中点,AD=BE,CD=CE.求证:∠A=∠B.
如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.求证:AE=BC.
6.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.线段BD、CE有怎样的数量关系和位置关系?写出你猜想的结论并加以证明.
如图,两根旗杆AC,BD相距10米,旗杆AC高3米,且AC⊥AB,BD⊥AB,一同学从B点出发向A点走去,当他走到点M时,发现自己刚好走了3米,此时他仰望旗杆的顶点C,D,又发现两条视线CM=DM. (1)求旗杆BD的高为多少米? (2)两条视线CM,DM有怎样的位置关系?请说明理由.
8. 已知:如图,∠1=∠2,∠D+∠C=180°.求证:AC=BD.
(四)角平分线的性质
1. 如图,△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,BD=5cm,则D点到AB的距离是 cm.
第1题 第2题 第3题 第4题
2. 如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是 .
3. 如图,∠AOB=30°,OP平分∠AOB,PC∥OB,PD⊥OB,如果PC=6,那么PD等于 .
4. 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于E,若△DEB的周长为10cm,则AB的长为 cm.
5. 如图,△ABO中,AD⊥OB于D,BC⊥OA于C,AD,BC交于点E,且OE平∠AOB,求证:AE=BE.
6.如图,△ABC的角平分线AD、BE相交于点P, (1)在图1中,分别画出点P到边AC、BC、BA的垂线段PF、PG、PH,这3条线段相等吗?为什么? (2)在图2中,∠ABC是直角,∠C=60°,其余条件都不变,请你判断并写出PE与PD之间的数量关系,并说明理由.
7.如图,已知∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上移动,两直角边分别与边OA,OB交于点C,D.求证:PC=PD.
8.如图,在四边形ABCD中,已知∠1=∠2,∠A+∠C=180°.求证:AD=CD.
9.如图,已知:Rt△ABC中,∠C=90°,AC=BC,AD是∠A的平分线.求证:AC+CD=AB.
【知识点】
角平分线的性质: ;
角平分线的判定: .
已知角平分线时,常用的辅助线是: ; .
四、检测
一、选择题:
1. 如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠AEC等于( )
A.60° B. 50° C. 45° D. 30°
第1题 第2题 第3题 第4题
如图,直线l过等腰直角△ABC顶点B,A、C两点到直线l的距离分别是2和3,则MN的长是( )
A.5 B. 4 C. 3 D. 2
如图,AC⊥BE,∠A=∠E,不能判断△ABC≌△EDC的条件是( )
A.BC=DC B.∠B=∠CDE C.AB=DE D.AC=CE
如图,折叠直角△ABC,使点C落在AB上的点E处.已知BC=12,∠B=30°,则DE的长是( )
A.6 B. 4 C. 3 D. 2
二、填空题:
5.如图,△ABC≌△DBF,∠ABD=30°,则∠CBF的度数为 °.
第5题 第6题 第7题
6.如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有 (填序号).
7.如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件 ,使得△EAB≌△BCD.
8.如图,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE= cm.
第8题 第9题 第10题
9.如图,在Rt△ABC中,∠C=90°,∠B=60°,∠A的平分线AD交BC于D,则= .
10.如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是 .
三、解答题:
11.如图:已知D、E分别在AB、AC上,AB=AC,∠B=∠C,求证:BE=CD.
12.已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点.求证:BD=AE.
13.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.直线BF垂直于直线CE于点F,交CD于点G,求证:AE=CG.
14.已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上. (1)如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之; (2)如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
检测答案
A 2. A 3. B 4. B 5. 30
①③④ 7. 答案不惟一,如BE=BD,AE=BC等 8.7 9. 10. 21
11.证明:在△ACD和△ABE中,
∴△ACD≌△AEB(ASA), ∴BE=CD.
12.证明:∵△ABC和△ECD都是等腰直角三角形, ∴AC=BC,CD=CE, ∵∠ACB=∠DCE=90°, ∴∠ACE+∠ACD=∠BCD+∠ACD, ∴∠ACE=∠BCD, 在△ACE和△BCD中,
∴△ACE≌△BCD(SAS), ∴BD=AE.
证明:∵AC=BC,∠ACB=90°,点D是AB的中点,
∴∠A=∠BCD=45°,∠ACE+∠BCF=90°,
∵BF⊥CE,
∴∠CBGE+∠BCF=90°,
∴∠ACE=∠CBG.
在△ACE和△BCG中,
∴△ACE≌△BCG(ASA), ∴AE=CG.
解:(1)关系是:AD+AB=AC 证明:∵AC平分∠MAN,∠MAN=120° ∴∠CAD=∠CAB=60° 又∠ADC=∠ABC=90°, ∴∠ACD=∠ACB=30° 则AD=AB=AC ∴AD+AB=AC; (2)仍成立.
证明:过点C分别作AM、AN的垂线,垂足分别为E、F, ∵AC平分∠MAN ∴CE=CF, ∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180° ∴∠CDE=∠ABC 又∠CED=∠CFB=90°,∴△CED≌△CFB(AAS), ∵ED=FB,∴AD+AB=AE-ED+AF+FB=AE+AF, 由(1)知AE+AF=AC, ∴AD+AB=AC.
