人教版(2019)物理必修第二册 5.4 抛体运动的规律课件(共38张PPT)
文档属性
| 名称 | 人教版(2019)物理必修第二册 5.4 抛体运动的规律课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-23 19:57:16 | ||
图片预览










文档简介
(共38张PPT)
5.4 抛体运动的规律
1. 理解抛体运动是匀变速运动。
2. 理论分析并推导平抛运动规律。
3. 了解探究一般抛体运动规律的方法。
在排球比赛中,你是否曾为排球下网或者出界而感到惋惜?如果运动员沿水平方向击球,在不计空气阻力的情况下,要使排球既能过网,又不出界,需要考虑哪些因素?如何估算球落地时的速度大小?
一、平抛运动的速度
平抛运动水平方向的速度有什么特点?大小如何?竖直方向的速度有什么特点?大小如何求得?如何确定某时刻物体的速度的大小和方向?
想一想:
1.在研究直线运动时,我们已经认识到,为了得到物体的速度与时间的关系,要先分析物体受到的力,由合力求出物体的加速度,进而得到物体的速度与时间的关系。关于平抛运动,我们仍然可以遵循这样的思路,只是要在相互垂直的两个方向上分别研究。
以速度沿水平方向抛出一物体,物体做平抛运动。以抛出点为原点,以初速度 的方向为x 轴方向,竖直向下的方向为y 轴方向,建立平面直角坐标系。
由于物体受到的重力是竖直向下的,它在x 方向的分力是0,根据牛顿运动定律,物体在 x 方向的加速度是 0;又由于物体在x 方向的分速度vx 在运动开始的时候是,所以它将保持 不变,与时间t 无关,即在整个运动过程中始终有
=
在y 方向受到的重力等于mg。以a 表示物体在y 方向的加速度,应用牛顿第二定律,得到mg = ma,所以a = g,即物体在竖直方向的加速度等于自由落体加速度。物体的初速度 沿x 方向,它在y 方向的分速度是 0,所以,物体在y 方向的分速度与时间t 的关系是
=gt
根据矢量运算法则,代表速度矢量v 和它的两个分矢量、的三个有向线段正好构成一个矩形的对角线和一对邻边。由勾股定理可知
V==
速度的方向可以由夹角θ 来表示。在图中,θ 是直角三角形的一个锐角,它的正切等于对边与邻边之比,即
tan θ = =
由上式可知,随着物体的下落,角θ 越来越大。也就是说,物体运动的方向越来越接近竖直向下的方向。这也与日常经验一致。
平抛运动的规律
1.平抛运动的特点:
项目 物理特性
理想化特点 物理上提出的平抛运动是一种理想化的模型,即把物体看成质点,抛出后只考虑重力作用,忽略空气阻力
速度 平抛运动的速度大小和方向都不断改变,故它是变速运动
加速度 平抛运动的加速度为自由落体加速度,恒定不变,故它是匀变速曲线运动
速度变化 做平抛运动的物体任意相等时间内速度变化量相等,均为Δv=gΔt,方向竖直向下
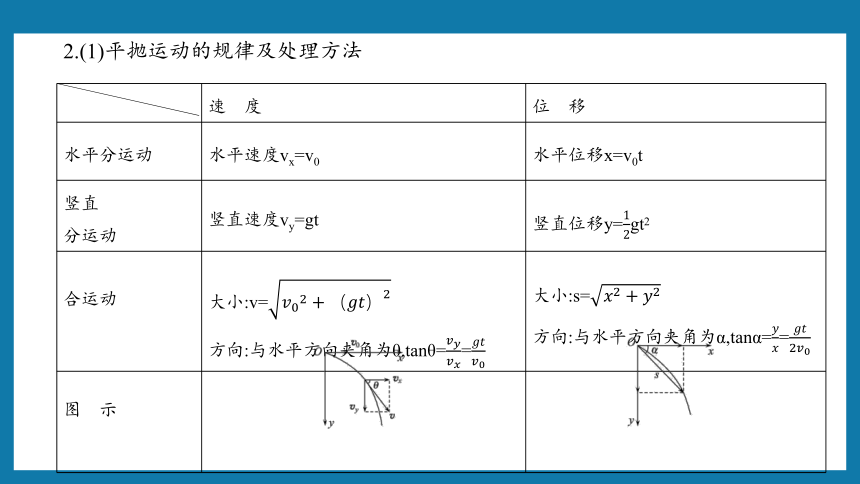
速 度 位 移
水平分运动 水平速度vx=v0 水平位移x=v0t
竖直 分运动 竖直速度vy=gt 竖直位移y=gt2
合运动 大小:v= 方向:与水平方向夹角为θ,tanθ== 大小:s=
方向:与水平方向夹角为α,tanα==
图 示
2.(1)平抛运动的规律及处理方法
(2)平抛运动的研究方法:研究平抛运动通常采用“化曲为直”的方法,即将平抛运动分解为竖直方向上的自由落体运动和水平方向上的匀速直线运动。
3.平抛运动时间的求解方法:
(1)利用水平位移或竖直位移求解时间:根据水平方向x=v0t或竖直方向y=gt2可求解时间。
(2)利用竖直分速度可求解时间:先求出竖直分速度,再根据vy=gt可求解时间。
(3)利用匀变速直线运动的推论Δy=gT2可求解时间。
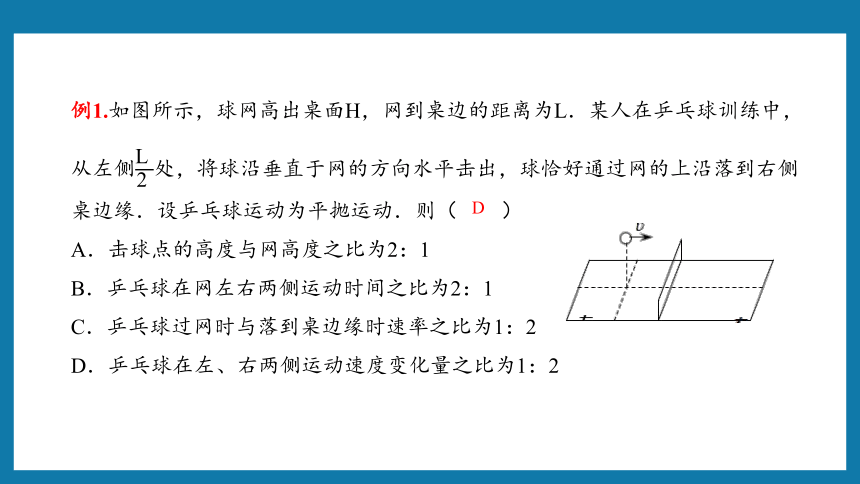
例1.如图所示,球网高出桌面H,网到桌边的距离为L.某人在乒乓球训练中,从左侧处,将球沿垂直于网的方向水平击出,球恰好通过网的上沿落到右侧桌边缘.设乒乓球运动为平抛运动.则( )
A.击球点的高度与网高度之比为2:1
B.乒乓球在网左右两侧运动时间之比为2:1
C.乒乓球过网时与落到桌边缘时速率之比为1:2
D.乒乓球在左、右两侧运动速度变化量之比为1:2
D
解析:A、因为水平方向做匀速运动,网右侧的水平位移是左边水平位移的两倍,所以由x=v0t知,网右侧运动时间是左侧的两倍,竖直方向做自由落体运动,根据h=g可知,在网上面运动的位移和整个高度之比为1:9,所以击球点的高度与网高之比为:9:8,故AB错误;
C、球恰好通过网的上沿的时间为落到右侧桌边缘的时间的,竖直方向做自由落体运动,根据v=gt可知,球恰好通过网的上沿的竖直分速度与落到右侧桌边缘的竖直分速度之比为1:3,根据v=可知,乒乓球过网时与落到桌边缘时速率之比不是1:2,故C错误;
D、网右侧运动时间是左侧的两倍,△v=gt,所以乒乓球在左、右两侧运动速度变化量之比为1:2;故D正确;
故选:D。
变式训练:
一名滑雪运动员练习跳台滑雪,第一次从斜坡的起点O水平飞出,落到斜坡上的A点,该运动员第二次从O点水平飞出时速度是第一次从O点飞出时速度的倍,已知OA=AB,不计空气阻力,下列判断不正确的是( )
A.两次飞行中速度变化率相同
B.第二次飞行运动员将落在AB之间
C.两次落到斜面时的速度方向与斜面之间的夹角相同
D.该运动员落到斜面时的速度大小是前一次落到斜面时速度的倍
B
解析:A、速度变化率相同即为加速度,两种情况下的加速度均为重力加速度g,所以两次飞行中速度变化率相同,A正确;B、设运动员平抛运动的水平位移为x、竖直位移为y,则有:x=t,y=g,tanθ==,解得:t=,则水平位移:x=t=;当速度为时水平位移x′=,所以运动员刚好落在B点,B错误;C、设运动员落到斜面时的速度方向与水平方向夹角为β,如图,根据速度方向偏向角与位移方向偏向角的关系可得,tanβ=2tanθ,所以两种情况下β相同,则两次落到斜面时的速度方向与斜面之间的夹角也相同,C正确;D、设运动员落到斜面上的速度为v,则:cosβ=,解得:v=,当该运动员第二次从O点水平飞出时速度是第一次从O点飞出时速度的倍时,运动员落到斜面时的速度大小是前一次落到斜面时速度的倍,D正确;
故选:B。
技法点拨:
平抛运动可以分解为在水平方向上的匀速直线运动,和竖直方向上的自由落体运动,分别根据匀速直线运动和自由落体运动的运动规律列方程求解即可.
1.平抛运动中的位移:
(1)水平方向:x=v0t
(2)竖直方向:y=gt2
2.物体的运动轨迹:y=,其中, 与x、y无关,具有y=a的形式,它的图像是一条抛物线。
二、平抛运动的位移与轨迹
平抛与斜面问题
1.常见的有两类问题:
(1)物体从斜面上某一点抛出以后又重新落在斜面上,此时平抛运动物体的合位移方向与水平方向的夹角等于斜面的倾角。
(2)做平抛运动的物体垂直打在斜面上,此时物体的合速度方向与斜面垂直。
题干信息 实例 处理方法或思路
速度 方向 垂直打在斜面上的平抛运动 (1)会速度分解图,确定速度与竖直方向的夹角
(2)根据水平方向和竖直方向的运动规律分析vx、vy
(3)根据tanθ=列方程求解
位移 方向 从斜面上水平抛出后又落在斜面上的平抛运动 (1)确定位移与水平方向的夹角α,画位移分解图
(2)根据水平方向和竖直方向的运动规律分析x、y
(3)根据tanα=列方程求解
2.基本求解思路:
例2.如图所示,乒乓球在球台上从O点弹起落在M点后,又弹起落在N点,两次弹起的最大高度相同,不考虑乒乓球的旋转和空气阻力。在上述两个过程中,下列说法正确的是( )
A.在最高点时加速度为零
B.在最高点时速度相等
C.两次弹起在空中的运动时间相等
D.在M点与台面碰撞前后速度大小相等
C
解析:A、不考虑乒乓球的旋转和空气阻力,乒乓球在空中运动时的加速度均为g,故A错误;
B、乒乓球每次从最高点到落在球台上做平抛运动,在最高点时水平速度不为零,故B错误;
C、两次的高度相同,由公式h=g可知,做平抛运动的时间相同,根据对称性可知,两次运动时间相等,故C正确;
D、由于高度相等,由公式=2gh可知,在M点与台面碰撞前后竖直方向的速度大小相等,且初速度大小不同,由平行四边形定则可知,在M点与台面碰撞前后速度大小不相等,故D错误。
故选:C。
变式训练:
在空间P点以初速度水平抛出一个小球,小球运动到空中A点时,速度与水平方向的夹角为60°,若在P点抛出的初速度方向不变,大小变为2,结果小球运动到空中B点时速度与水平方向的夹角也为60°,不计空气阻力,则下列说法正确的是( )
A.PB长是PA长的2倍
B.PB长是PA长的4倍
C.PA与水平方向的夹角小于PB与水平方向的夹角
D.PA与水平方向的夹角大于PB与水平方向的夹角
B
解析:
CD、小球到达A点,PA为位移,设PA与水平方向的夹角为θ,则有tanθ=tan60°,小球到达B点,PB为位移,设PB与水平方向的夹角为α,则有tanα=tan60°,因此PA与水平方向的夹角等于PB与水平方向的夹角,故CD错误;
AB、因为θ=α,可知P、A、B在同一直线上,假设PAB为斜面,小球从P点运动到A点的时间为 t1=,水平位移为x1=v0t1=,则SPA=
=,同理可得 SPB=,因此PB为PA的4倍,故A错误,B正确;
故选:B。
技法点拨:
由运动的合成与分解规律,水平方向做匀速直线运动,竖直方向做竖直上抛运动,过程中加速度相同,由竖直高度相同,由运动学公式分析可知道水平初速度的关系.两次在最高点的速度等于水平初速度.由速度合成分析初速度的关系,即可知道落地速度的大小关系.
三、一般的抛体运动
1.抛体运动的方向:初速度方向斜向上或斜向下。
2.运动性质:由于物体只受重力,所以抛体运动是匀变速曲线运动。
3.分析方法:斜抛运动可以看成是水平方向的匀速直线运动和竖直方向的匀变速直线运动的合运动。
4.初速度:水平方向:=cosθ;竖直方向:= sinθ 。
1.斜抛运动的规律:
(1)速度规律。
水平速度:v0x=v0cosθ。
竖直速度:v0y=v0sinθ-gt。
t时刻的速度大小为v=。
(2)位移规律。
水平位移:x=v0xt=v0tcosθ。
竖直位移:y=v0tsinθ-gt2。
t时间内的位移大小为s=,与水平方向成α角,且tanα=。
2.射高和射程:
(1)斜抛运动的飞行时间:t= =
(2)射高:h==
(3)射程:s=cosθ·t== 对于给定的,当θ=45°时,射程达到最大值, =。
3.一般抛体运动问题的分析思路:一般抛体运动问题的处理方法和平抛运动的处理方法相同,都是将运动分解为两个方向的简单的直线运动,分别为水平方向的匀速直线运动和竖直方向的匀变速直线运动。
例3.某人玩抛球游戏,从同一位置以相同大小的速度v抛出甲、乙和丙三个不同的小球,抛出点距落地点的高度差均为h,甲球竖直上抛,乙球竖直下抛,丙球水平抛出,空气阻力不计,则以下说法正确的是( )
A.甲、乙、丙从抛出点到落地点的位移相同
B.甲、乙、丙三球落地速度相同
C.甲、乙、丙三球运动加速度相同
D.甲、乙、丙从抛出到落地重力做的功一定相同
C
解析:A、以大地为参考系,甲做竖直上抛运动,乙做竖直下抛运动,丙做平抛运动,则甲和乙的位移相同,丙的位移最大,故A错误;
B、三小球沿着不同的方向抛出,都只有重力做功,每个小球的机械能守恒,故可得到落地时速度大小相等,但方向不同,故B错误;
C、小球沿着不同的方向抛出,都只受重力作用,三小球运动的加速度均相同,故C正确;
D、三个小球抛出点距落地点的高度差均为h,但三个小球的质量不一定相同,则从抛出到落地过程中重力做功W=mgh不一定相同,故D错误;
故选:C。
变式训练:
如图所示,将一小球从固定斜面顶端A以某一速度水平向右抛出,恰好落到斜面底端B.若初速度不变,对小球施加不为零的竖直方向的恒力F,使小球落到AB连线之间的某点C.不计空气阻力。则( )
A.小球落到B点与落到C点的速度方向一定相同
B.小球落到B点与落到C点的速度大小一定不同
C.小球落到C点时的速度方向可能竖直向下
D.力F越大,小球落到斜面的时间越长
A
解析:
AB、A小球从A到B做平抛运动,加恒力F后,从A到C做类平抛运动,两次都落在斜面上,故位移偏向角相等,则速度偏向角也相等,初速度相同,所以末速度也相同,故A正确,B错误;
C、小球有水平方向的速度,故C错误;
D、力F竖直向下,力越大,竖直方向的加速度越大,小球落到斜面的时间越短,故D错误;
故选:A。
技法点拨:
沿不同方向抛出的小球都只有重力做功,机械能守恒;同时速度是矢量,大小相等、方向相同时速度才是相同的,要有矢量意识.
1.关于平抛运动,下列说法正确的是( )
A.平抛运动是非匀变速运动
B.平抛运动是匀速运动
C.平抛运动是匀变速曲线运动
D.平抛运动的物体落地时速度方向一定是竖直向下的
解析:A、B错,C对:平抛运动的加速度不变,是匀变速曲线运动。
D错:落地时有水平分速度,合速度方向不会竖直向下。
故选:C。
C
2.如图所示,某公园有喷水装置,若水从小鱼模型口中水平喷出,忽略空气阻力及水之间的相互作用,下列说法中正确的是( )
A.喷水口高度一定,喷水速度越大,水从喷出到落入池中的时间越短
B.喷水口高度一定,喷水速度越大,水喷得越近
C.喷水速度一定,喷水高度越高,水喷得越近
D.喷水口高度一定,喷水速度越大,水从喷出到落人池中的时间不变
解析:设水做平抛运动的初速度为v,抛出时的高度为h,下落的时间为t,则由h=g,得t=,水平方向的位移:x=vt=v。ABD、喷水高度一定,则运动时间一定,喷水速度越大,水平位移越大,故AB错误,D正确;C、喷水速度一定,喷水高度越高,运动时间和水平位移就越大,水喷得越远,故C错误;
故选:D。
D
3.做平抛运动的物体,在相等的两段时间内( )
A.动能变化相同
B.发生的位移相等
C.速度的变化量相等
D.平均速度相等
解析:A、物体做平抛运动,只受重力,相等时间内,重力方向上的位移不等,重力做功不等,根据动能定理可知,动能变化不等,故A错误;
BD、物体做平抛运动,在相等时间内水平方向上的位移相等,竖直方向上的位移不等,则相等时间内经过的位移不等,根据平均速度的定义可知,平均速度不等,故BD错误;
C、平抛运动的加速度不变,根据△v=g△t知相等时间内速度的变化量相等,故C正确。
故选:C。
C
4.如图,某一小球以v0=10 m/s的速度水平抛出,在落地之前经过空中A、B两点,在A点小球的速度与水平方向的夹角为45°,在B点小球的速度与水平方向的夹角为60°,空气阻力忽略不计,g取10 m/s2,求:
(1)小球在B点的速度大小;
(2)A、B两点间水平距离xAB的值。
解析:(1)如图甲,在B点=tan 60°,解得=10 m/s,
==20 m/s。
(2)如图乙,在A点=tan 45°,解得=10 m/s。
小球从A点运动到B点的时间t==( -1) s。
则A、B两点间的水平距离=t=10( -1) m。
再见
5.4 抛体运动的规律
1. 理解抛体运动是匀变速运动。
2. 理论分析并推导平抛运动规律。
3. 了解探究一般抛体运动规律的方法。
在排球比赛中,你是否曾为排球下网或者出界而感到惋惜?如果运动员沿水平方向击球,在不计空气阻力的情况下,要使排球既能过网,又不出界,需要考虑哪些因素?如何估算球落地时的速度大小?
一、平抛运动的速度
平抛运动水平方向的速度有什么特点?大小如何?竖直方向的速度有什么特点?大小如何求得?如何确定某时刻物体的速度的大小和方向?
想一想:
1.在研究直线运动时,我们已经认识到,为了得到物体的速度与时间的关系,要先分析物体受到的力,由合力求出物体的加速度,进而得到物体的速度与时间的关系。关于平抛运动,我们仍然可以遵循这样的思路,只是要在相互垂直的两个方向上分别研究。
以速度沿水平方向抛出一物体,物体做平抛运动。以抛出点为原点,以初速度 的方向为x 轴方向,竖直向下的方向为y 轴方向,建立平面直角坐标系。
由于物体受到的重力是竖直向下的,它在x 方向的分力是0,根据牛顿运动定律,物体在 x 方向的加速度是 0;又由于物体在x 方向的分速度vx 在运动开始的时候是,所以它将保持 不变,与时间t 无关,即在整个运动过程中始终有
=
在y 方向受到的重力等于mg。以a 表示物体在y 方向的加速度,应用牛顿第二定律,得到mg = ma,所以a = g,即物体在竖直方向的加速度等于自由落体加速度。物体的初速度 沿x 方向,它在y 方向的分速度是 0,所以,物体在y 方向的分速度与时间t 的关系是
=gt
根据矢量运算法则,代表速度矢量v 和它的两个分矢量、的三个有向线段正好构成一个矩形的对角线和一对邻边。由勾股定理可知
V==
速度的方向可以由夹角θ 来表示。在图中,θ 是直角三角形的一个锐角,它的正切等于对边与邻边之比,即
tan θ = =
由上式可知,随着物体的下落,角θ 越来越大。也就是说,物体运动的方向越来越接近竖直向下的方向。这也与日常经验一致。
平抛运动的规律
1.平抛运动的特点:
项目 物理特性
理想化特点 物理上提出的平抛运动是一种理想化的模型,即把物体看成质点,抛出后只考虑重力作用,忽略空气阻力
速度 平抛运动的速度大小和方向都不断改变,故它是变速运动
加速度 平抛运动的加速度为自由落体加速度,恒定不变,故它是匀变速曲线运动
速度变化 做平抛运动的物体任意相等时间内速度变化量相等,均为Δv=gΔt,方向竖直向下
速 度 位 移
水平分运动 水平速度vx=v0 水平位移x=v0t
竖直 分运动 竖直速度vy=gt 竖直位移y=gt2
合运动 大小:v= 方向:与水平方向夹角为θ,tanθ== 大小:s=
方向:与水平方向夹角为α,tanα==
图 示
2.(1)平抛运动的规律及处理方法
(2)平抛运动的研究方法:研究平抛运动通常采用“化曲为直”的方法,即将平抛运动分解为竖直方向上的自由落体运动和水平方向上的匀速直线运动。
3.平抛运动时间的求解方法:
(1)利用水平位移或竖直位移求解时间:根据水平方向x=v0t或竖直方向y=gt2可求解时间。
(2)利用竖直分速度可求解时间:先求出竖直分速度,再根据vy=gt可求解时间。
(3)利用匀变速直线运动的推论Δy=gT2可求解时间。
例1.如图所示,球网高出桌面H,网到桌边的距离为L.某人在乒乓球训练中,从左侧处,将球沿垂直于网的方向水平击出,球恰好通过网的上沿落到右侧桌边缘.设乒乓球运动为平抛运动.则( )
A.击球点的高度与网高度之比为2:1
B.乒乓球在网左右两侧运动时间之比为2:1
C.乒乓球过网时与落到桌边缘时速率之比为1:2
D.乒乓球在左、右两侧运动速度变化量之比为1:2
D
解析:A、因为水平方向做匀速运动,网右侧的水平位移是左边水平位移的两倍,所以由x=v0t知,网右侧运动时间是左侧的两倍,竖直方向做自由落体运动,根据h=g可知,在网上面运动的位移和整个高度之比为1:9,所以击球点的高度与网高之比为:9:8,故AB错误;
C、球恰好通过网的上沿的时间为落到右侧桌边缘的时间的,竖直方向做自由落体运动,根据v=gt可知,球恰好通过网的上沿的竖直分速度与落到右侧桌边缘的竖直分速度之比为1:3,根据v=可知,乒乓球过网时与落到桌边缘时速率之比不是1:2,故C错误;
D、网右侧运动时间是左侧的两倍,△v=gt,所以乒乓球在左、右两侧运动速度变化量之比为1:2;故D正确;
故选:D。
变式训练:
一名滑雪运动员练习跳台滑雪,第一次从斜坡的起点O水平飞出,落到斜坡上的A点,该运动员第二次从O点水平飞出时速度是第一次从O点飞出时速度的倍,已知OA=AB,不计空气阻力,下列判断不正确的是( )
A.两次飞行中速度变化率相同
B.第二次飞行运动员将落在AB之间
C.两次落到斜面时的速度方向与斜面之间的夹角相同
D.该运动员落到斜面时的速度大小是前一次落到斜面时速度的倍
B
解析:A、速度变化率相同即为加速度,两种情况下的加速度均为重力加速度g,所以两次飞行中速度变化率相同,A正确;B、设运动员平抛运动的水平位移为x、竖直位移为y,则有:x=t,y=g,tanθ==,解得:t=,则水平位移:x=t=;当速度为时水平位移x′=,所以运动员刚好落在B点,B错误;C、设运动员落到斜面时的速度方向与水平方向夹角为β,如图,根据速度方向偏向角与位移方向偏向角的关系可得,tanβ=2tanθ,所以两种情况下β相同,则两次落到斜面时的速度方向与斜面之间的夹角也相同,C正确;D、设运动员落到斜面上的速度为v,则:cosβ=,解得:v=,当该运动员第二次从O点水平飞出时速度是第一次从O点飞出时速度的倍时,运动员落到斜面时的速度大小是前一次落到斜面时速度的倍,D正确;
故选:B。
技法点拨:
平抛运动可以分解为在水平方向上的匀速直线运动,和竖直方向上的自由落体运动,分别根据匀速直线运动和自由落体运动的运动规律列方程求解即可.
1.平抛运动中的位移:
(1)水平方向:x=v0t
(2)竖直方向:y=gt2
2.物体的运动轨迹:y=,其中, 与x、y无关,具有y=a的形式,它的图像是一条抛物线。
二、平抛运动的位移与轨迹
平抛与斜面问题
1.常见的有两类问题:
(1)物体从斜面上某一点抛出以后又重新落在斜面上,此时平抛运动物体的合位移方向与水平方向的夹角等于斜面的倾角。
(2)做平抛运动的物体垂直打在斜面上,此时物体的合速度方向与斜面垂直。
题干信息 实例 处理方法或思路
速度 方向 垂直打在斜面上的平抛运动 (1)会速度分解图,确定速度与竖直方向的夹角
(2)根据水平方向和竖直方向的运动规律分析vx、vy
(3)根据tanθ=列方程求解
位移 方向 从斜面上水平抛出后又落在斜面上的平抛运动 (1)确定位移与水平方向的夹角α,画位移分解图
(2)根据水平方向和竖直方向的运动规律分析x、y
(3)根据tanα=列方程求解
2.基本求解思路:
例2.如图所示,乒乓球在球台上从O点弹起落在M点后,又弹起落在N点,两次弹起的最大高度相同,不考虑乒乓球的旋转和空气阻力。在上述两个过程中,下列说法正确的是( )
A.在最高点时加速度为零
B.在最高点时速度相等
C.两次弹起在空中的运动时间相等
D.在M点与台面碰撞前后速度大小相等
C
解析:A、不考虑乒乓球的旋转和空气阻力,乒乓球在空中运动时的加速度均为g,故A错误;
B、乒乓球每次从最高点到落在球台上做平抛运动,在最高点时水平速度不为零,故B错误;
C、两次的高度相同,由公式h=g可知,做平抛运动的时间相同,根据对称性可知,两次运动时间相等,故C正确;
D、由于高度相等,由公式=2gh可知,在M点与台面碰撞前后竖直方向的速度大小相等,且初速度大小不同,由平行四边形定则可知,在M点与台面碰撞前后速度大小不相等,故D错误。
故选:C。
变式训练:
在空间P点以初速度水平抛出一个小球,小球运动到空中A点时,速度与水平方向的夹角为60°,若在P点抛出的初速度方向不变,大小变为2,结果小球运动到空中B点时速度与水平方向的夹角也为60°,不计空气阻力,则下列说法正确的是( )
A.PB长是PA长的2倍
B.PB长是PA长的4倍
C.PA与水平方向的夹角小于PB与水平方向的夹角
D.PA与水平方向的夹角大于PB与水平方向的夹角
B
解析:
CD、小球到达A点,PA为位移,设PA与水平方向的夹角为θ,则有tanθ=tan60°,小球到达B点,PB为位移,设PB与水平方向的夹角为α,则有tanα=tan60°,因此PA与水平方向的夹角等于PB与水平方向的夹角,故CD错误;
AB、因为θ=α,可知P、A、B在同一直线上,假设PAB为斜面,小球从P点运动到A点的时间为 t1=,水平位移为x1=v0t1=,则SPA=
=,同理可得 SPB=,因此PB为PA的4倍,故A错误,B正确;
故选:B。
技法点拨:
由运动的合成与分解规律,水平方向做匀速直线运动,竖直方向做竖直上抛运动,过程中加速度相同,由竖直高度相同,由运动学公式分析可知道水平初速度的关系.两次在最高点的速度等于水平初速度.由速度合成分析初速度的关系,即可知道落地速度的大小关系.
三、一般的抛体运动
1.抛体运动的方向:初速度方向斜向上或斜向下。
2.运动性质:由于物体只受重力,所以抛体运动是匀变速曲线运动。
3.分析方法:斜抛运动可以看成是水平方向的匀速直线运动和竖直方向的匀变速直线运动的合运动。
4.初速度:水平方向:=cosθ;竖直方向:= sinθ 。
1.斜抛运动的规律:
(1)速度规律。
水平速度:v0x=v0cosθ。
竖直速度:v0y=v0sinθ-gt。
t时刻的速度大小为v=。
(2)位移规律。
水平位移:x=v0xt=v0tcosθ。
竖直位移:y=v0tsinθ-gt2。
t时间内的位移大小为s=,与水平方向成α角,且tanα=。
2.射高和射程:
(1)斜抛运动的飞行时间:t= =
(2)射高:h==
(3)射程:s=cosθ·t== 对于给定的,当θ=45°时,射程达到最大值, =。
3.一般抛体运动问题的分析思路:一般抛体运动问题的处理方法和平抛运动的处理方法相同,都是将运动分解为两个方向的简单的直线运动,分别为水平方向的匀速直线运动和竖直方向的匀变速直线运动。
例3.某人玩抛球游戏,从同一位置以相同大小的速度v抛出甲、乙和丙三个不同的小球,抛出点距落地点的高度差均为h,甲球竖直上抛,乙球竖直下抛,丙球水平抛出,空气阻力不计,则以下说法正确的是( )
A.甲、乙、丙从抛出点到落地点的位移相同
B.甲、乙、丙三球落地速度相同
C.甲、乙、丙三球运动加速度相同
D.甲、乙、丙从抛出到落地重力做的功一定相同
C
解析:A、以大地为参考系,甲做竖直上抛运动,乙做竖直下抛运动,丙做平抛运动,则甲和乙的位移相同,丙的位移最大,故A错误;
B、三小球沿着不同的方向抛出,都只有重力做功,每个小球的机械能守恒,故可得到落地时速度大小相等,但方向不同,故B错误;
C、小球沿着不同的方向抛出,都只受重力作用,三小球运动的加速度均相同,故C正确;
D、三个小球抛出点距落地点的高度差均为h,但三个小球的质量不一定相同,则从抛出到落地过程中重力做功W=mgh不一定相同,故D错误;
故选:C。
变式训练:
如图所示,将一小球从固定斜面顶端A以某一速度水平向右抛出,恰好落到斜面底端B.若初速度不变,对小球施加不为零的竖直方向的恒力F,使小球落到AB连线之间的某点C.不计空气阻力。则( )
A.小球落到B点与落到C点的速度方向一定相同
B.小球落到B点与落到C点的速度大小一定不同
C.小球落到C点时的速度方向可能竖直向下
D.力F越大,小球落到斜面的时间越长
A
解析:
AB、A小球从A到B做平抛运动,加恒力F后,从A到C做类平抛运动,两次都落在斜面上,故位移偏向角相等,则速度偏向角也相等,初速度相同,所以末速度也相同,故A正确,B错误;
C、小球有水平方向的速度,故C错误;
D、力F竖直向下,力越大,竖直方向的加速度越大,小球落到斜面的时间越短,故D错误;
故选:A。
技法点拨:
沿不同方向抛出的小球都只有重力做功,机械能守恒;同时速度是矢量,大小相等、方向相同时速度才是相同的,要有矢量意识.
1.关于平抛运动,下列说法正确的是( )
A.平抛运动是非匀变速运动
B.平抛运动是匀速运动
C.平抛运动是匀变速曲线运动
D.平抛运动的物体落地时速度方向一定是竖直向下的
解析:A、B错,C对:平抛运动的加速度不变,是匀变速曲线运动。
D错:落地时有水平分速度,合速度方向不会竖直向下。
故选:C。
C
2.如图所示,某公园有喷水装置,若水从小鱼模型口中水平喷出,忽略空气阻力及水之间的相互作用,下列说法中正确的是( )
A.喷水口高度一定,喷水速度越大,水从喷出到落入池中的时间越短
B.喷水口高度一定,喷水速度越大,水喷得越近
C.喷水速度一定,喷水高度越高,水喷得越近
D.喷水口高度一定,喷水速度越大,水从喷出到落人池中的时间不变
解析:设水做平抛运动的初速度为v,抛出时的高度为h,下落的时间为t,则由h=g,得t=,水平方向的位移:x=vt=v。ABD、喷水高度一定,则运动时间一定,喷水速度越大,水平位移越大,故AB错误,D正确;C、喷水速度一定,喷水高度越高,运动时间和水平位移就越大,水喷得越远,故C错误;
故选:D。
D
3.做平抛运动的物体,在相等的两段时间内( )
A.动能变化相同
B.发生的位移相等
C.速度的变化量相等
D.平均速度相等
解析:A、物体做平抛运动,只受重力,相等时间内,重力方向上的位移不等,重力做功不等,根据动能定理可知,动能变化不等,故A错误;
BD、物体做平抛运动,在相等时间内水平方向上的位移相等,竖直方向上的位移不等,则相等时间内经过的位移不等,根据平均速度的定义可知,平均速度不等,故BD错误;
C、平抛运动的加速度不变,根据△v=g△t知相等时间内速度的变化量相等,故C正确。
故选:C。
C
4.如图,某一小球以v0=10 m/s的速度水平抛出,在落地之前经过空中A、B两点,在A点小球的速度与水平方向的夹角为45°,在B点小球的速度与水平方向的夹角为60°,空气阻力忽略不计,g取10 m/s2,求:
(1)小球在B点的速度大小;
(2)A、B两点间水平距离xAB的值。
解析:(1)如图甲,在B点=tan 60°,解得=10 m/s,
==20 m/s。
(2)如图乙,在A点=tan 45°,解得=10 m/s。
小球从A点运动到B点的时间t==( -1) s。
则A、B两点间的水平距离=t=10( -1) m。
再见
