人教版(2019)物理必修第二册 8.4 机械能守恒定律课件(共35张PPT)
文档属性
| 名称 | 人教版(2019)物理必修第二册 8.4 机械能守恒定律课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-23 20:08:05 | ||
图片预览








文档简介
(共35张PPT)
8.4 机械能守恒定律
1. 知道机械能的各种形式.
2.能够分析动能与势能(包括弹性势能)之间的相互转化问题.
3.知道机械能守恒的条件,写出机械能守恒定律的表达式.
4.会判断机械能是否守恒,运用机械能守恒定律解决有关问题.
学习重点:在具体的问题中能判定机械能是否守恒,并能列出定律的数学表达式.
学习难点:从能的转化和功能关系出发理解机械能守恒的条件.
思考:过山车在运动过程中,虽然没有什么动力,但为什么每次总能如此准确的完成一连串有惊无险的动作呢?
这实际上是动能和势能之间发生了相互转化,那么你知道它们在转化的过程中遵守什么规律吗?
一、动能与势能的相互转化
1.追寻守恒量
伽利略理想斜面实验视频
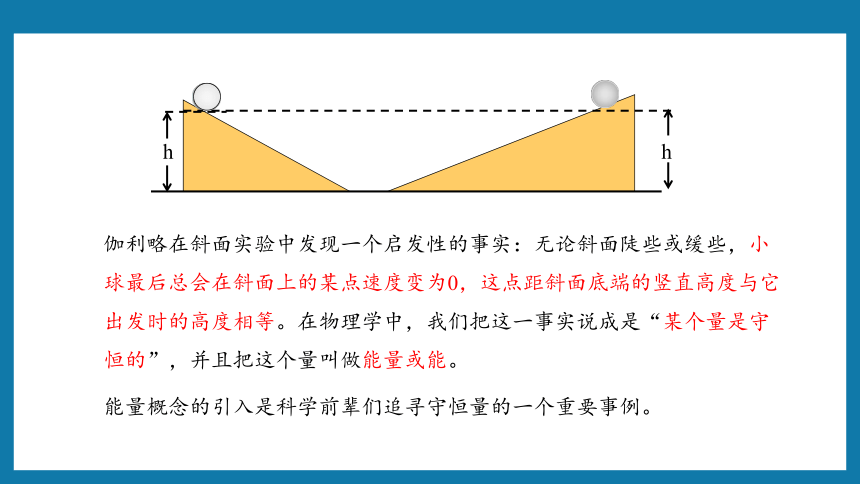
伽利略在斜面实验中发现一个启发性的事实:无论斜面陡些或缓些,小球最后总会在斜面上的某点速度变为0,这点距斜面底端的竖直高度与它出发时的高度相等。在物理学中,我们把这一事实说成是“某个量是守恒的”,并且把这个量叫做能量或能。
h
h
能量概念的引入是科学前辈们追寻守恒量的一个重要事例。
2.动能与势能的相互转化
(1)重力势能与动能相互转化
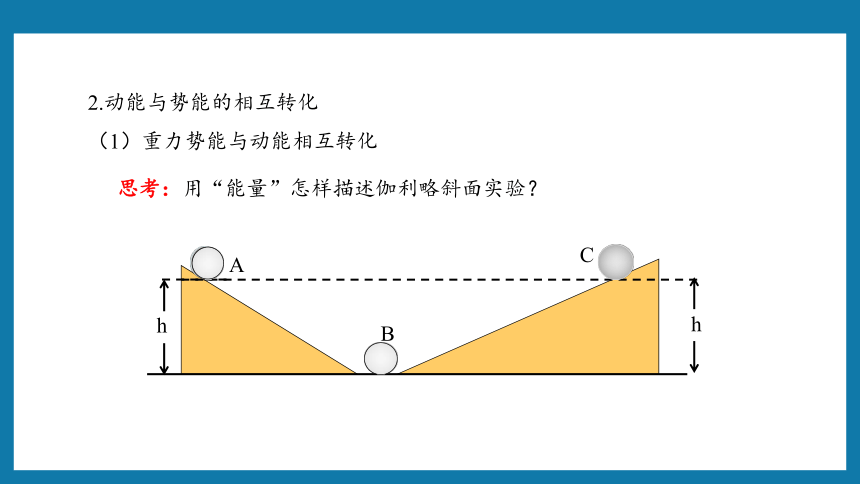
思考:用“能量”怎样描述伽利略斜面实验?
h
h
A
B
C
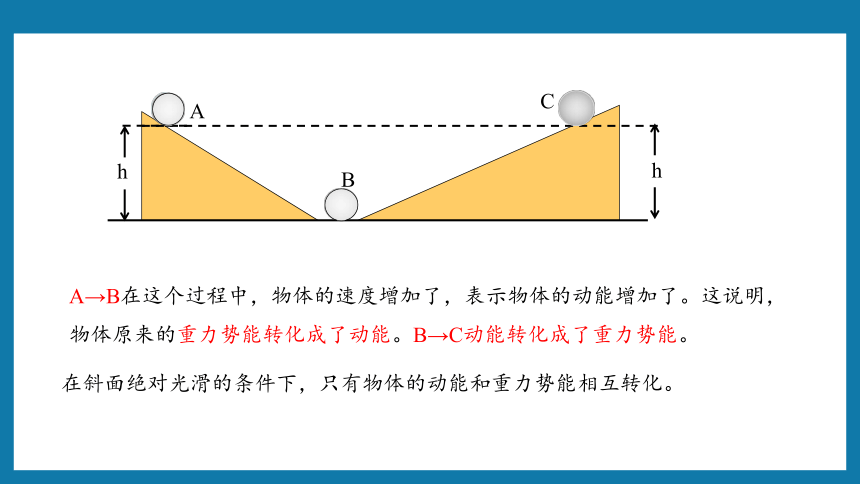
在斜面绝对光滑的条件下,只有物体的动能和重力势能相互转化。
A→B在这个过程中,物体的速度增加了,表示物体的动能增加了。这说明,物体原来的重力势能转化成了动能。B→C动能转化成了重力势能。
h
h
A
B
C
(2)弹性势能与动能相互转化
弯弓射箭时,弓的弹性势能转化成箭的动能。
篮球跳动的过程中动能和弹性势能的转化。
3.机械能
(1)物体的动能和势能之和为物体的机械能,它包括动能、重力势能和弹性势能。
(2)机械能是一个状态量,做机械运动的物体在某一位置时 ,具有确定的速度,也就有确定的动能和势能,即具有确定的机械能。
(3)机械能具有相对性,其大小与参考系、参考平面的选取有关。
(4)机械能是标量,是系统共有的。
(5)通过重力或弹力做功,机械能可以从一种形式转化成另一种形式。
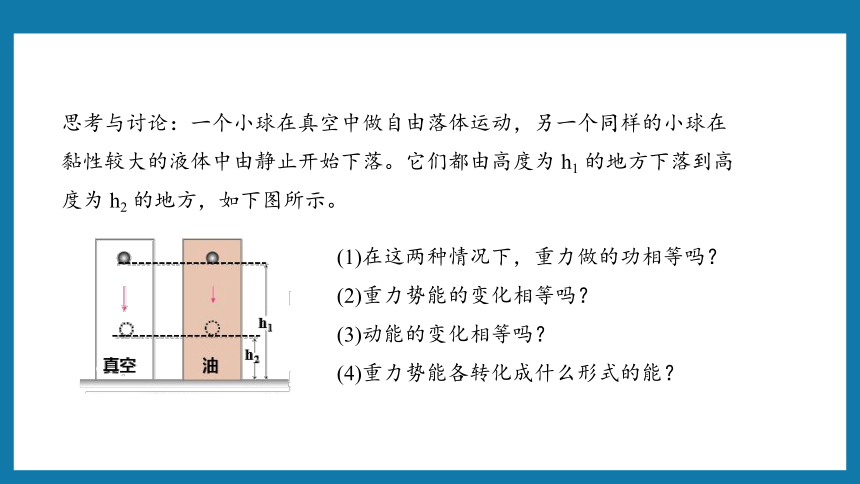
思考与讨论:一个小球在真空中做自由落体运动,另一个同样的小球在黏性较大的液体中由静止开始下落。它们都由高度为 h1 的地方下落到高度为 h2 的地方,如下图所示。
(1)在这两种情况下,重力做的功相等吗?
(2)重力势能的变化相等吗?
(3)动能的变化相等吗?
(4)重力势能各转化成什么形式的能?
参考答案:
(1)这两种情况下,重力做功相等;
(2)重力势能的变化相等;
(3)动能变化不相等;
(4)第一次减小的重力势能完全转化为动能,第二次减小的重力势能除了转化为动能外,还有一部分转化为内能。
例1. 如图所示,物体A在拉力F的作用下向上做加速运动,在这一过程中( )
A.动能不变,重力势能增加,机械能增加
B.动能增加,重力势能不变,机械能增加
C.动能增加,重力势能增加,机械能增加
D.动能不变,重力势能不变,机械能不变
C
F
v
变式训练:
如图所示,小球沿轨道由静止从A处运动到D处的过程中,忽略空气阻力和摩擦力,仅有动能和重力势能间的相互转化,则( )
A.小球在A处的动能等于在D处的动能
B.小球在C处的动能大于在B处的动能
C.小球在B处的机械能小于在D处的机械能
D.小球在B处的机械能等于在A处的机械能
D
A
C
D
B
技法点拨:
小球在运动的过程中没有能量损耗,故其在各处的机械能都相等。小球在A处时高度最高,重力势能最大,动能最小;小球在B处时高度最小,重力势能最小,但动能最大。
二、机械能守恒定律
例如:如图物体沿光滑曲面滑下的情形。这种情形下,物体受到哪些力的作用?哪些力做功?
思考:动能与势能的相互转化是否存在某种定量的关系?
重力和曲面支持力的作用,因为支持力方向与运动方向垂直,支持力不做功,所以,只有重力做功。
如图所示物体在某一时刻处在高度为 h1 的位置A,这时它的速度是 v1 。经过一段时间后,物体下落到高度为 h2 的另一位置 B,这时它的速度是 v2 。
另一方面,重力对物体做的功等于物体重力势能的减少。即:
从动能定理知道,重力对物体做的功等于物体动能的增加,即:
进一步整理可得:
从以上两式可得:
这就是说,重力做了多少功,就有多少重力势能转化为动能。
等式左边为物体末状态动能与势能之和,等式右边为物体初状态动能与势能之和。
结论:在只有重力做功的系统内,动能与重力势能互相转化时总的机械能保持不变。
思考:在上图中,如果物体从位置 B 沿光滑曲面上升到位置 A,重力做负功。这种情况下上式的关系是否还成立?
另一方面,重力对物体做的负功等于物体重力势能的增加。
即:
由动能定理得:
进一步整理可得:
从以上两式可得:
这就是说,重力做了多少功,就有多少重力势能转化为动能。
这种情况下上式的关系仍然成立。
1.机械能守恒定律内容
在只有重力或弹力做功的物体系统内,动能和势能可以相互转化,而总的机械能保持不变,这叫作机械能守恒定律。
2. 条件
只有系统内的重力或弹力做功,其他力不做功或做功的代数和为零。
3. 常用表达式
(1)守恒观点:系统的初状态机械能的总和与末状态机械能的的零势能面,且初、末状总和相等。
EK1 + EP1 = EK2 + EP2
注意:应用时应选好重力势能态必须用同一 零势能面计算势能。
(2)转化观点:表示系统(或物体)机械能守恒时, 系统减少(或增加)的重力势能等于系统增加(或减少)的动能。
EK=- Ep
应用时的关键在于分清重力势能的增加量或减少量,可不选零势能面而直接计算初、末状态的势能差。
例1. 把一个小球用细线悬挂起来,就成为一个摆如图所示,摆长为 l,最大偏角为 θ。如果阻力可以忽略,小球运动到最低点时的速度大小是多少?
解:以小球为研究对象。设最低点的重力势能为 0,以小球在最高点的状态作为初状态,以小球在最低点的状态作为末状态。
在最高点的动能 Ek1=0,重力势能是Ep1=mg(l - l cos θ)
在最低点的重力势能 Ep2 = 0,而动能可以表示为:
由此解出小球运动到最低点时的速度大小:
从得到的表达式可以看出,初状态的 θ 角越大,cosθ 越小,(1-cos θ )
就越大,v 也就越大。也就是说,最初把小球拉得越高,它到达最低点时的速度也就越大。
运动过程中只有重力做功,所以机械能守恒,即:Ek2+Ep2 = Ek1+Ep1
把初末状态下动能、重力势能的表达式代入,得
=mg(L-L cos θ)
4.利用机械能守恒定律解题思路
(1)选取研究对象
(2)根据研究对象所经历的物理过程,进行受力,做功分析,判断机械能是否守恒。
(3)恰当地选取参考平面,确定研究对象在过程的初末时刻的机械能。
(4)根据机械能守恒定律列方程,进行求解。
变式训练:如图所示,A物体用板托着,离地高度h=4.0m,轻质细绳通过光滑定滑轮与A、B相连,绳子处于绷直状态。已知A物体质量M=3.0kg,B物体质量m=2.0kg,现将板抽走,A将拉动B上升,设A着地后不反弹,B上升过程中不会碰到定滑轮,g取10m/s2。求:
(1)A着地时,B的速度大小;
(2)B物体在上升过程中离地面的最大高度。
参考答案: (1)4m/s;(2)4.8m
技法点拨:
(1)A、B组成的系统,只有重力做功,系统机械能守恒。
(2)A落地后,B物体仅受重力,机械能守恒
机械能守恒定律
机械能守恒定律的内容
表达式:EK1 + EP1 = EK2 + EP2
守恒条件
机械能守恒定律
动能与势能的相互转化
机械能
重力势能
弹性势能
动能
1.关于机械能是否守恒的叙述,正确的是( )
A. 做匀速直线运动的物体的机械能不一定守恒
B. 只有重力对物体做功,物体机械能不一定守恒
C. 做匀变速运动的物体机械能一定守恒
D. 外力对物体做功为零时,机械能一定守恒
A
2. 在下面各实例中,机械能守恒的是( )
A. 在空中做平抛运动的铅球
B. 在空中匀速下降的跳伞运动员
C. 随电梯加速上升的学生
D. 在蹦极运动过程中,运动员的机械能始终守恒
A
3.一物体从地面由静止开始运动,取地面为零势能面,运动过程中重力对物体做功W1,阻力对物体做功W2,其他力对物体做功W3,则该过程终态时( )
A. 物体的动能为W1 +W2
B. 物体的重力势能为W1
C. 物体的机械能为W2 +W3
D. 物体的机械能为W1 +W2 +W3
C
4. (多选)自由下落的小球,从接触竖直放置的轻弹簧开始,到压缩弹簧有最大形变的过程中,以下说法中正确的是( )
小球的动能逐渐减少
B. 小球的重力势能逐渐减少
C. 小球的机械能不守恒
D. 小球的加速度逐渐增大
BC
5. (多选) 下列说法中正确的是( )
A.用绳子拉着物体匀速上升,只有重力和弹力对物体做功,物体的机械能守恒
B.做竖直上抛运动的物体,只有重力对它做功,机械能守恒
C.沿光滑斜面自由下滑的物体,只有重力对物体做功,机械能守恒
D.用水平拉力使物体沿光滑水平面匀加速运动,机械能守恒
BC
再见
8.4 机械能守恒定律
1. 知道机械能的各种形式.
2.能够分析动能与势能(包括弹性势能)之间的相互转化问题.
3.知道机械能守恒的条件,写出机械能守恒定律的表达式.
4.会判断机械能是否守恒,运用机械能守恒定律解决有关问题.
学习重点:在具体的问题中能判定机械能是否守恒,并能列出定律的数学表达式.
学习难点:从能的转化和功能关系出发理解机械能守恒的条件.
思考:过山车在运动过程中,虽然没有什么动力,但为什么每次总能如此准确的完成一连串有惊无险的动作呢?
这实际上是动能和势能之间发生了相互转化,那么你知道它们在转化的过程中遵守什么规律吗?
一、动能与势能的相互转化
1.追寻守恒量
伽利略理想斜面实验视频
伽利略在斜面实验中发现一个启发性的事实:无论斜面陡些或缓些,小球最后总会在斜面上的某点速度变为0,这点距斜面底端的竖直高度与它出发时的高度相等。在物理学中,我们把这一事实说成是“某个量是守恒的”,并且把这个量叫做能量或能。
h
h
能量概念的引入是科学前辈们追寻守恒量的一个重要事例。
2.动能与势能的相互转化
(1)重力势能与动能相互转化
思考:用“能量”怎样描述伽利略斜面实验?
h
h
A
B
C
在斜面绝对光滑的条件下,只有物体的动能和重力势能相互转化。
A→B在这个过程中,物体的速度增加了,表示物体的动能增加了。这说明,物体原来的重力势能转化成了动能。B→C动能转化成了重力势能。
h
h
A
B
C
(2)弹性势能与动能相互转化
弯弓射箭时,弓的弹性势能转化成箭的动能。
篮球跳动的过程中动能和弹性势能的转化。
3.机械能
(1)物体的动能和势能之和为物体的机械能,它包括动能、重力势能和弹性势能。
(2)机械能是一个状态量,做机械运动的物体在某一位置时 ,具有确定的速度,也就有确定的动能和势能,即具有确定的机械能。
(3)机械能具有相对性,其大小与参考系、参考平面的选取有关。
(4)机械能是标量,是系统共有的。
(5)通过重力或弹力做功,机械能可以从一种形式转化成另一种形式。
思考与讨论:一个小球在真空中做自由落体运动,另一个同样的小球在黏性较大的液体中由静止开始下落。它们都由高度为 h1 的地方下落到高度为 h2 的地方,如下图所示。
(1)在这两种情况下,重力做的功相等吗?
(2)重力势能的变化相等吗?
(3)动能的变化相等吗?
(4)重力势能各转化成什么形式的能?
参考答案:
(1)这两种情况下,重力做功相等;
(2)重力势能的变化相等;
(3)动能变化不相等;
(4)第一次减小的重力势能完全转化为动能,第二次减小的重力势能除了转化为动能外,还有一部分转化为内能。
例1. 如图所示,物体A在拉力F的作用下向上做加速运动,在这一过程中( )
A.动能不变,重力势能增加,机械能增加
B.动能增加,重力势能不变,机械能增加
C.动能增加,重力势能增加,机械能增加
D.动能不变,重力势能不变,机械能不变
C
F
v
变式训练:
如图所示,小球沿轨道由静止从A处运动到D处的过程中,忽略空气阻力和摩擦力,仅有动能和重力势能间的相互转化,则( )
A.小球在A处的动能等于在D处的动能
B.小球在C处的动能大于在B处的动能
C.小球在B处的机械能小于在D处的机械能
D.小球在B处的机械能等于在A处的机械能
D
A
C
D
B
技法点拨:
小球在运动的过程中没有能量损耗,故其在各处的机械能都相等。小球在A处时高度最高,重力势能最大,动能最小;小球在B处时高度最小,重力势能最小,但动能最大。
二、机械能守恒定律
例如:如图物体沿光滑曲面滑下的情形。这种情形下,物体受到哪些力的作用?哪些力做功?
思考:动能与势能的相互转化是否存在某种定量的关系?
重力和曲面支持力的作用,因为支持力方向与运动方向垂直,支持力不做功,所以,只有重力做功。
如图所示物体在某一时刻处在高度为 h1 的位置A,这时它的速度是 v1 。经过一段时间后,物体下落到高度为 h2 的另一位置 B,这时它的速度是 v2 。
另一方面,重力对物体做的功等于物体重力势能的减少。即:
从动能定理知道,重力对物体做的功等于物体动能的增加,即:
进一步整理可得:
从以上两式可得:
这就是说,重力做了多少功,就有多少重力势能转化为动能。
等式左边为物体末状态动能与势能之和,等式右边为物体初状态动能与势能之和。
结论:在只有重力做功的系统内,动能与重力势能互相转化时总的机械能保持不变。
思考:在上图中,如果物体从位置 B 沿光滑曲面上升到位置 A,重力做负功。这种情况下上式的关系是否还成立?
另一方面,重力对物体做的负功等于物体重力势能的增加。
即:
由动能定理得:
进一步整理可得:
从以上两式可得:
这就是说,重力做了多少功,就有多少重力势能转化为动能。
这种情况下上式的关系仍然成立。
1.机械能守恒定律内容
在只有重力或弹力做功的物体系统内,动能和势能可以相互转化,而总的机械能保持不变,这叫作机械能守恒定律。
2. 条件
只有系统内的重力或弹力做功,其他力不做功或做功的代数和为零。
3. 常用表达式
(1)守恒观点:系统的初状态机械能的总和与末状态机械能的的零势能面,且初、末状总和相等。
EK1 + EP1 = EK2 + EP2
注意:应用时应选好重力势能态必须用同一 零势能面计算势能。
(2)转化观点:表示系统(或物体)机械能守恒时, 系统减少(或增加)的重力势能等于系统增加(或减少)的动能。
EK=- Ep
应用时的关键在于分清重力势能的增加量或减少量,可不选零势能面而直接计算初、末状态的势能差。
例1. 把一个小球用细线悬挂起来,就成为一个摆如图所示,摆长为 l,最大偏角为 θ。如果阻力可以忽略,小球运动到最低点时的速度大小是多少?
解:以小球为研究对象。设最低点的重力势能为 0,以小球在最高点的状态作为初状态,以小球在最低点的状态作为末状态。
在最高点的动能 Ek1=0,重力势能是Ep1=mg(l - l cos θ)
在最低点的重力势能 Ep2 = 0,而动能可以表示为:
由此解出小球运动到最低点时的速度大小:
从得到的表达式可以看出,初状态的 θ 角越大,cosθ 越小,(1-cos θ )
就越大,v 也就越大。也就是说,最初把小球拉得越高,它到达最低点时的速度也就越大。
运动过程中只有重力做功,所以机械能守恒,即:Ek2+Ep2 = Ek1+Ep1
把初末状态下动能、重力势能的表达式代入,得
=mg(L-L cos θ)
4.利用机械能守恒定律解题思路
(1)选取研究对象
(2)根据研究对象所经历的物理过程,进行受力,做功分析,判断机械能是否守恒。
(3)恰当地选取参考平面,确定研究对象在过程的初末时刻的机械能。
(4)根据机械能守恒定律列方程,进行求解。
变式训练:如图所示,A物体用板托着,离地高度h=4.0m,轻质细绳通过光滑定滑轮与A、B相连,绳子处于绷直状态。已知A物体质量M=3.0kg,B物体质量m=2.0kg,现将板抽走,A将拉动B上升,设A着地后不反弹,B上升过程中不会碰到定滑轮,g取10m/s2。求:
(1)A着地时,B的速度大小;
(2)B物体在上升过程中离地面的最大高度。
参考答案: (1)4m/s;(2)4.8m
技法点拨:
(1)A、B组成的系统,只有重力做功,系统机械能守恒。
(2)A落地后,B物体仅受重力,机械能守恒
机械能守恒定律
机械能守恒定律的内容
表达式:EK1 + EP1 = EK2 + EP2
守恒条件
机械能守恒定律
动能与势能的相互转化
机械能
重力势能
弹性势能
动能
1.关于机械能是否守恒的叙述,正确的是( )
A. 做匀速直线运动的物体的机械能不一定守恒
B. 只有重力对物体做功,物体机械能不一定守恒
C. 做匀变速运动的物体机械能一定守恒
D. 外力对物体做功为零时,机械能一定守恒
A
2. 在下面各实例中,机械能守恒的是( )
A. 在空中做平抛运动的铅球
B. 在空中匀速下降的跳伞运动员
C. 随电梯加速上升的学生
D. 在蹦极运动过程中,运动员的机械能始终守恒
A
3.一物体从地面由静止开始运动,取地面为零势能面,运动过程中重力对物体做功W1,阻力对物体做功W2,其他力对物体做功W3,则该过程终态时( )
A. 物体的动能为W1 +W2
B. 物体的重力势能为W1
C. 物体的机械能为W2 +W3
D. 物体的机械能为W1 +W2 +W3
C
4. (多选)自由下落的小球,从接触竖直放置的轻弹簧开始,到压缩弹簧有最大形变的过程中,以下说法中正确的是( )
小球的动能逐渐减少
B. 小球的重力势能逐渐减少
C. 小球的机械能不守恒
D. 小球的加速度逐渐增大
BC
5. (多选) 下列说法中正确的是( )
A.用绳子拉着物体匀速上升,只有重力和弹力对物体做功,物体的机械能守恒
B.做竖直上抛运动的物体,只有重力对它做功,机械能守恒
C.沿光滑斜面自由下滑的物体,只有重力对物体做功,机械能守恒
D.用水平拉力使物体沿光滑水平面匀加速运动,机械能守恒
BC
再见
