4.3《角》课时练习题(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版七年级数学上册第四章《4.3角》课时练习题(含答案)
一、单选题
1.下列各度数的角,能借助一副三角尺画出的是( )
A.55° B.65° C.75° D.85°
2.如图所示,正方形网格中有和,如果每个小正方形的边长都为1,估测与的大小关系为( )
A. B. C. D.无法估测
3.下列换算中,正确的是( )
A. B.
C. D.
4.已知,则的余角是( )
A. B. C. D.
5.已知∠A=38°,则∠A的补角的度数是( )
A.52° B.62° C.142° D.162°
6.如图,在同一平面内,,,点为反向延长线上一点(图中所有角均指小于的角).下列结论:
①;
②;
③;
④.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
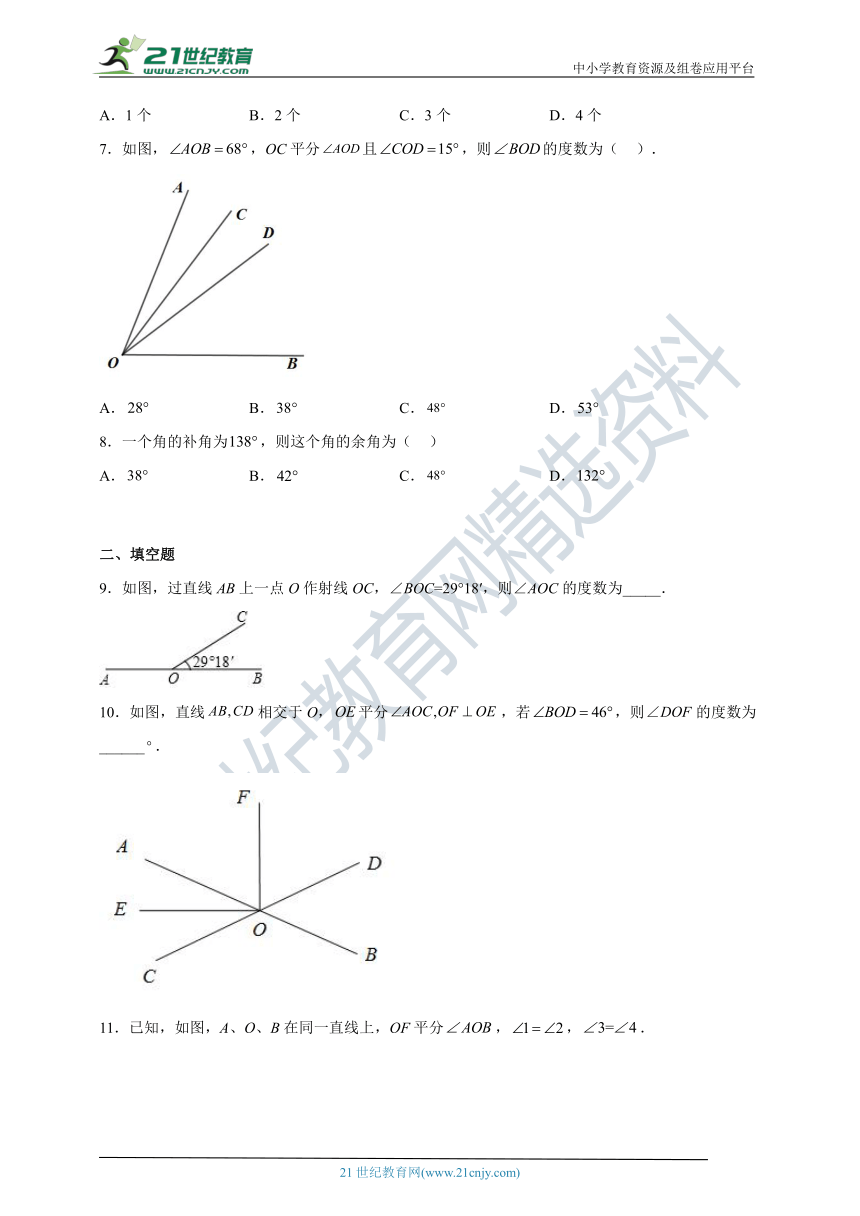
7.如图,,OC平分且,则的度数为( ).
A. B. C. D.
8.一个角的补角为,则这个角的余角为( )
A. B. C. D.
二、填空题
9.如图,过直线AB上一点O作射线OC,∠BOC=29°18′,则∠AOC的度数为_____.
10.如图,直线相交于O,平分,若,则的度数为______.
11.已知,如图,A、O、B在同一直线上,OF平分,,.
(1)射线OD是_______的角平分线;(2)的补角是_______;(3)的余角是_______;(4)_______是的余角;(5)的补角是_______;(6)_______是的补角.
12.如图,若OC、OD三等分,则______________,_______,_______.
13.如图,已知∠AOB=90°,射线OC在∠AOB内部,OD平分∠AOC,OE平分∠BOC,则∠DOE=_____°.
14.如图,将一副三角尺的两个锐角(30°角和45°角)的顶点P叠放在一起,没有重叠的部分分别记作∠1和∠2,若∠1与∠2的和为61°,则∠APC的度数是 _____.
三、解答题
15.如图,点P是直线l外一点,过点P画直线PA,PB,PC,…,分别交直线l于点A,B,C,….用量角器量出,,的度数,并量出PA,PB,PC的长度,你发现了什么?
16.如图,两个直角三角形的直角顶点重合,∠AOC=40°,求∠BOD的度数.结合图形,完成填空:
解:因为∠AOC+∠COB= °,
∠COB+∠BOD= ①
所以∠AOC= .②
因为∠AOC=40°,
所以∠BOD= °.
在上面①到②的推导过程中,理由依据是: .
17.如图①,已知线段AB=18cm,CD=2cm,线段CD在线段AB上运动,E,F分别是AC,BD的中点.
(1)若AC=4cm,则EF= cm;
(2)当线段CD在线段AB上运动时,试判断EF的长度是否发生变化?如果不变,请求出EF的长度,如果变化,请说明理由.
(3)a.我们发现角的很多规律和线段一样,如图②,已知∠COD在∠AOB内部转动,OE,OF分别平分∠AOC和∠BOD,若∠AOB=140°,∠COD=40°,求∠EOF.
b.由此,你猜想∠EOF,∠AOB和∠COD会有怎样的数量关系 .(直接写出猜想即可)
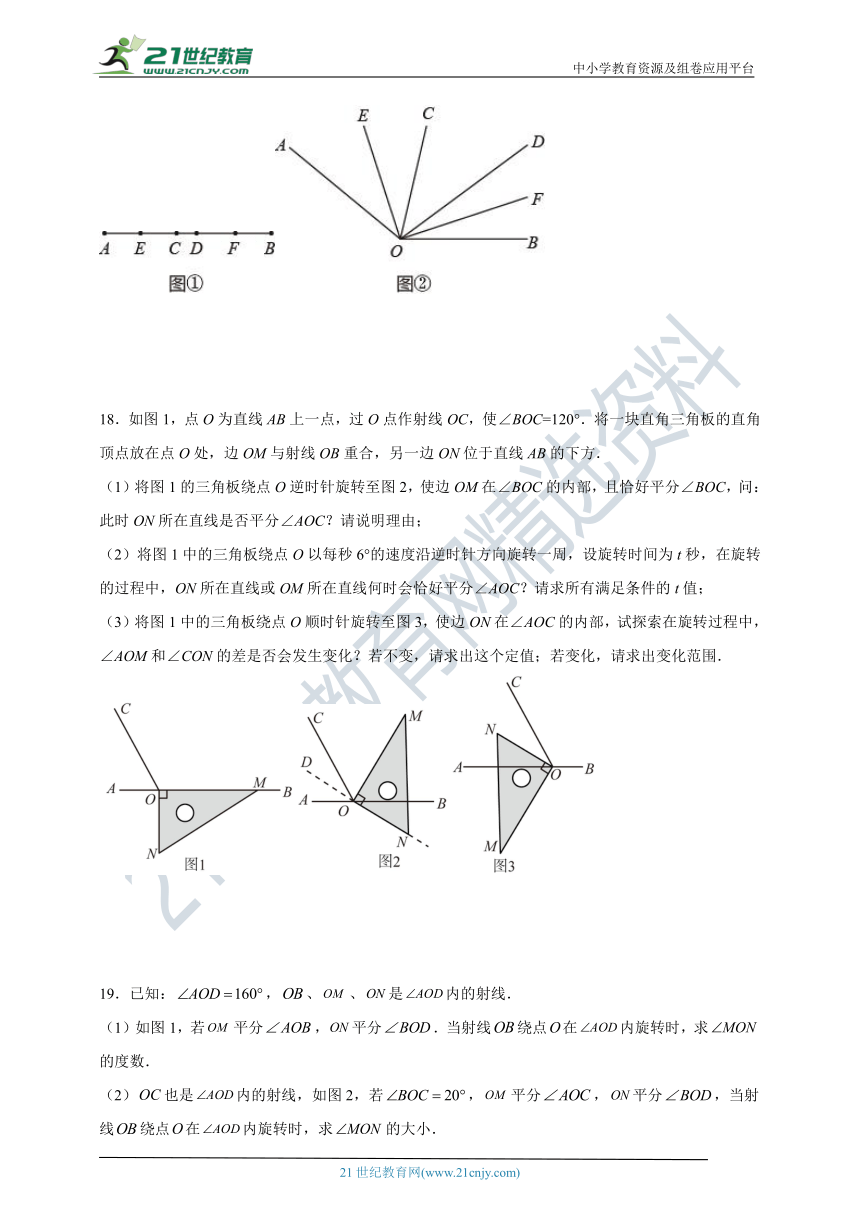
18.如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°.将一块直角三角板的直角顶点放在点O处,边OM与射线OB重合,另一边ON位于直线AB的下方.
(1)将图1的三角板绕点O逆时针旋转至图2,使边OM在∠BOC的内部,且恰好平分∠BOC,问:此时ON所在直线是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,设旋转时间为t秒,在旋转的过程中,ON所在直线或OM所在直线何时会恰好平分∠AOC?请求所有满足条件的t值;
(3)将图1中的三角板绕点O顺时针旋转至图3,使边ON在∠AOC的内部,试探索在旋转过程中,∠AOM和∠CON的差是否会发生变化?若不变,请求出这个定值;若变化,请求出变化范围.
19.已知:,、、是内的射线.
(1)如图1,若平分,平分.当射线绕点在内旋转时,求的度数.
(2)也是内的射线,如图2,若,平分,平分,当射线绕点在内旋转时,求的大小.
20.【阅读理解】
定义:在一条直线同侧的三条具有公共端点的射线之间若满足以下关系,其中一条射线分别与另外两条射线组成的角恰好满足2倍的数量关系,则称该射线是另外两条射线的“双倍和谐线”.如图1,点P在直线l上,射线PR,PS,PT位于直线l同侧,若PS平分∠RPT,则有∠RPT=2∠RPS,所以我们称射线PR是射线PS,PT的“双倍和谐线”.
【迁移运用】
(1)如图1,射线PS (选填“是”或“不是”)射线PR,PT的“双倍和谐线”;射线PT (选填“是”或“不是”)射线PS,PR的“双倍和谐线”;
(2)如图2,点O在直线MN上,OAMN,∠AOB=40°,射线OC从ON出发,绕点O以每秒4°的速度逆时针旋转,运动时间为t秒,当射线OC与射线OA重合时,运动停止.
①当射线OA是射线OB,OC的“双倍和谐线”时,求t的值;
②若在射线OC旋转的同时,∠AOB绕点O以每秒2°的速度逆时针旋转,且在旋转过程中,射线OD平分∠AOB.当射线OC位于射线OD左侧且射线OC是射线OM,OD的“双倍和谐线”时,求∠CON的度数。
参考答案
1.C2.A3.B4.A5.C6.C7.B8.C
9.150°42′
10.67
11. 和 和
12. 3 AOD
13.45°.
14.68°
15.解:量得,,,,,,
由此发现,在P点与直线上的点的连线中,与直线的夹角越大(不超过),P点与直线交点连线的线段长度越短;反之亦然.
16.解:因为∠AOC+∠COB= 90 °,
∠COB+∠BOD= 90 ° -﹣﹣﹣①
所以∠AOC= ∠BOD .﹣﹣﹣﹣②-
因为∠AOC=40°,
所以∠BOD= 40 °.
在上面①到②的推导过程中,理由依据是:同角的余角相等.
故答案为:90,90,∠BOD,40,同角的余角相等.
17.解:(1)∵E,F分别是AC,BD的中点,
∴EC=,DF=.
∴EC+DF=.
又∵AB=18cm,CD=2cm,
∴AC+DB=AB﹣CD=18﹣2=16(cm).
∴EC+DF==8(cm).
∴EF=EC+DF+CD=8+2=10(cm).
故答案为:10.
(2)不变,理由如下:
∵E,F分别是AC,BD的中点,
∴EC=,DF=.
∴EC+DF=.
∴EF=EC+DF+CD=CD+=,
又∵AB=18cm,CD=2cm,
∴EF==10(cm).
(3)a:∵OE,OF分别平分∠AOC和∠BOD,
∴∠EOC=,∠DOF=.
∴∠EOC+∠DOF==.
又∵∠AOB=140°,∠COD=40°,
∴∠AOC+∠BOD=∠AOB﹣∠COD=100°.
∴∠EOC+∠DOF=50°.
∴∠EOF=∠EOC+∠DOF+∠COD=50°+40°=90°.
b:由(1)得:∠EOC+∠DOF=.
∵∠AOC+∠DOB=∠AOB﹣∠COD,
∴∠EOC+∠DOF=.
∴∠EOF=∠EOC+∠DOF+∠COD=+∠COD=.
18.解:(1)直线ON平分∠AOC
理由:设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB,
又∵OM⊥ON,
∴∠MOD=∠MON=90°,
∴∠COD=∠BON,
又∵∠AOD=∠BON,
∴∠COD=∠AOD,
∴OD平分∠AOC,即直线ON平分∠AOC;
(2)①当直线ON平分∠AOC时,
三角板旋转角度为60°或240°,
∵旋转速度为6°/秒,
∴t=10秒或40秒;
②当直线OM平分∠AOC时,
三角板旋转角度为150°或330°,
∴t=25秒或55秒,
综上所述:t=10秒或40秒或25秒或55秒;
(3)设∠AON=x°,则∠CON=60°-x°,∠AOM=90°-x°,
∴∠AOM-∠CON=30°,
∴∠AOM与∠CON差不会改变,为定值30°.
19.解:(1)∵平分,
∴
∵平分,
∴
∴
(2)∵平分,
∴,
∵平分,
∴
∴
=
20.(1)解:∵PS平分∠RPT,
∴∠RPS=∠TPS,
∴射线PS不是射线PR,PT的“双倍和谐线”;
∵PS平分∠RPT,
∴∠TPR=2∠TPS.
∴射线PT是射线PS,PR的“双倍和谐线”.
故答案为:不是;是;
(2)①由题意得:∠AOC=90°-4°t,∠AOB=40°.
∵射线OA是射线OB,OC的“双倍和谐线”,
∴∠AOC=2∠AOB或∠AOB=2∠AOC.
当∠AOC=2∠AOB时,如图,
则:90-4t=2×40.
解得:t=,
当∠AOB=2∠AOC时,如图,
则:40=2(90-4t).
解得:t=,
综上,当射线OA是射线OB,OC的“双倍和谐线”时,t的值为或;
②由题意得:∠CON=4°t,∠AON=90°+2°t,∠AOD=20°,∠DON=∠AON-∠AOD=70°+2°t.
∵当射线OC与射线OA重合时,运动停止,
∴此时∠AON=∠CON.
∴90+2t=4t.
∴t=45.
∴当t=45秒时,运动停止,此时∠AON=180°.
∵射线OC位于射线OD左侧且射线OC是射线OM,OD的“双倍和谐线”,
∴∠COM=2∠COD或∠COD=2∠COM.
当∠COM=2∠COD时,如图,
即:180°-∠CON=2(∠CON-∠DON),
则:180-4t=2(4t-70-2t).
解得:t=40.
∴∠CON=4°×40=160°.
当∠COD=2∠COM时,如图,
即:∠CON-∠DON=2(180°-∠CON).
则:4t-(70+2t)=2(180-4t).
解得:t=43.
∴∠CON=4°×43=172°.
综上,当射线OC位于射线OD左侧且射线OC是射线OM,OD的“双倍和谐线”时,∠CON的度数为160°或172°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版七年级数学上册第四章《4.3角》课时练习题(含答案)
一、单选题
1.下列各度数的角,能借助一副三角尺画出的是( )
A.55° B.65° C.75° D.85°
2.如图所示,正方形网格中有和,如果每个小正方形的边长都为1,估测与的大小关系为( )
A. B. C. D.无法估测
3.下列换算中,正确的是( )
A. B.
C. D.
4.已知,则的余角是( )
A. B. C. D.
5.已知∠A=38°,则∠A的补角的度数是( )
A.52° B.62° C.142° D.162°
6.如图,在同一平面内,,,点为反向延长线上一点(图中所有角均指小于的角).下列结论:
①;
②;
③;
④.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
7.如图,,OC平分且,则的度数为( ).
A. B. C. D.
8.一个角的补角为,则这个角的余角为( )
A. B. C. D.
二、填空题
9.如图,过直线AB上一点O作射线OC,∠BOC=29°18′,则∠AOC的度数为_____.
10.如图,直线相交于O,平分,若,则的度数为______.
11.已知,如图,A、O、B在同一直线上,OF平分,,.
(1)射线OD是_______的角平分线;(2)的补角是_______;(3)的余角是_______;(4)_______是的余角;(5)的补角是_______;(6)_______是的补角.
12.如图,若OC、OD三等分,则______________,_______,_______.
13.如图,已知∠AOB=90°,射线OC在∠AOB内部,OD平分∠AOC,OE平分∠BOC,则∠DOE=_____°.
14.如图,将一副三角尺的两个锐角(30°角和45°角)的顶点P叠放在一起,没有重叠的部分分别记作∠1和∠2,若∠1与∠2的和为61°,则∠APC的度数是 _____.
三、解答题
15.如图,点P是直线l外一点,过点P画直线PA,PB,PC,…,分别交直线l于点A,B,C,….用量角器量出,,的度数,并量出PA,PB,PC的长度,你发现了什么?
16.如图,两个直角三角形的直角顶点重合,∠AOC=40°,求∠BOD的度数.结合图形,完成填空:
解:因为∠AOC+∠COB= °,
∠COB+∠BOD= ①
所以∠AOC= .②
因为∠AOC=40°,
所以∠BOD= °.
在上面①到②的推导过程中,理由依据是: .
17.如图①,已知线段AB=18cm,CD=2cm,线段CD在线段AB上运动,E,F分别是AC,BD的中点.
(1)若AC=4cm,则EF= cm;
(2)当线段CD在线段AB上运动时,试判断EF的长度是否发生变化?如果不变,请求出EF的长度,如果变化,请说明理由.
(3)a.我们发现角的很多规律和线段一样,如图②,已知∠COD在∠AOB内部转动,OE,OF分别平分∠AOC和∠BOD,若∠AOB=140°,∠COD=40°,求∠EOF.
b.由此,你猜想∠EOF,∠AOB和∠COD会有怎样的数量关系 .(直接写出猜想即可)
18.如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°.将一块直角三角板的直角顶点放在点O处,边OM与射线OB重合,另一边ON位于直线AB的下方.
(1)将图1的三角板绕点O逆时针旋转至图2,使边OM在∠BOC的内部,且恰好平分∠BOC,问:此时ON所在直线是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,设旋转时间为t秒,在旋转的过程中,ON所在直线或OM所在直线何时会恰好平分∠AOC?请求所有满足条件的t值;
(3)将图1中的三角板绕点O顺时针旋转至图3,使边ON在∠AOC的内部,试探索在旋转过程中,∠AOM和∠CON的差是否会发生变化?若不变,请求出这个定值;若变化,请求出变化范围.
19.已知:,、、是内的射线.
(1)如图1,若平分,平分.当射线绕点在内旋转时,求的度数.
(2)也是内的射线,如图2,若,平分,平分,当射线绕点在内旋转时,求的大小.
20.【阅读理解】
定义:在一条直线同侧的三条具有公共端点的射线之间若满足以下关系,其中一条射线分别与另外两条射线组成的角恰好满足2倍的数量关系,则称该射线是另外两条射线的“双倍和谐线”.如图1,点P在直线l上,射线PR,PS,PT位于直线l同侧,若PS平分∠RPT,则有∠RPT=2∠RPS,所以我们称射线PR是射线PS,PT的“双倍和谐线”.
【迁移运用】
(1)如图1,射线PS (选填“是”或“不是”)射线PR,PT的“双倍和谐线”;射线PT (选填“是”或“不是”)射线PS,PR的“双倍和谐线”;
(2)如图2,点O在直线MN上,OAMN,∠AOB=40°,射线OC从ON出发,绕点O以每秒4°的速度逆时针旋转,运动时间为t秒,当射线OC与射线OA重合时,运动停止.
①当射线OA是射线OB,OC的“双倍和谐线”时,求t的值;
②若在射线OC旋转的同时,∠AOB绕点O以每秒2°的速度逆时针旋转,且在旋转过程中,射线OD平分∠AOB.当射线OC位于射线OD左侧且射线OC是射线OM,OD的“双倍和谐线”时,求∠CON的度数。
参考答案
1.C2.A3.B4.A5.C6.C7.B8.C
9.150°42′
10.67
11. 和 和
12. 3 AOD
13.45°.
14.68°
15.解:量得,,,,,,
由此发现,在P点与直线上的点的连线中,与直线的夹角越大(不超过),P点与直线交点连线的线段长度越短;反之亦然.
16.解:因为∠AOC+∠COB= 90 °,
∠COB+∠BOD= 90 ° -﹣﹣﹣①
所以∠AOC= ∠BOD .﹣﹣﹣﹣②-
因为∠AOC=40°,
所以∠BOD= 40 °.
在上面①到②的推导过程中,理由依据是:同角的余角相等.
故答案为:90,90,∠BOD,40,同角的余角相等.
17.解:(1)∵E,F分别是AC,BD的中点,
∴EC=,DF=.
∴EC+DF=.
又∵AB=18cm,CD=2cm,
∴AC+DB=AB﹣CD=18﹣2=16(cm).
∴EC+DF==8(cm).
∴EF=EC+DF+CD=8+2=10(cm).
故答案为:10.
(2)不变,理由如下:
∵E,F分别是AC,BD的中点,
∴EC=,DF=.
∴EC+DF=.
∴EF=EC+DF+CD=CD+=,
又∵AB=18cm,CD=2cm,
∴EF==10(cm).
(3)a:∵OE,OF分别平分∠AOC和∠BOD,
∴∠EOC=,∠DOF=.
∴∠EOC+∠DOF==.
又∵∠AOB=140°,∠COD=40°,
∴∠AOC+∠BOD=∠AOB﹣∠COD=100°.
∴∠EOC+∠DOF=50°.
∴∠EOF=∠EOC+∠DOF+∠COD=50°+40°=90°.
b:由(1)得:∠EOC+∠DOF=.
∵∠AOC+∠DOB=∠AOB﹣∠COD,
∴∠EOC+∠DOF=.
∴∠EOF=∠EOC+∠DOF+∠COD=+∠COD=.
18.解:(1)直线ON平分∠AOC
理由:设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB,
又∵OM⊥ON,
∴∠MOD=∠MON=90°,
∴∠COD=∠BON,
又∵∠AOD=∠BON,
∴∠COD=∠AOD,
∴OD平分∠AOC,即直线ON平分∠AOC;
(2)①当直线ON平分∠AOC时,
三角板旋转角度为60°或240°,
∵旋转速度为6°/秒,
∴t=10秒或40秒;
②当直线OM平分∠AOC时,
三角板旋转角度为150°或330°,
∴t=25秒或55秒,
综上所述:t=10秒或40秒或25秒或55秒;
(3)设∠AON=x°,则∠CON=60°-x°,∠AOM=90°-x°,
∴∠AOM-∠CON=30°,
∴∠AOM与∠CON差不会改变,为定值30°.
19.解:(1)∵平分,
∴
∵平分,
∴
∴
(2)∵平分,
∴,
∵平分,
∴
∴
=
20.(1)解:∵PS平分∠RPT,
∴∠RPS=∠TPS,
∴射线PS不是射线PR,PT的“双倍和谐线”;
∵PS平分∠RPT,
∴∠TPR=2∠TPS.
∴射线PT是射线PS,PR的“双倍和谐线”.
故答案为:不是;是;
(2)①由题意得:∠AOC=90°-4°t,∠AOB=40°.
∵射线OA是射线OB,OC的“双倍和谐线”,
∴∠AOC=2∠AOB或∠AOB=2∠AOC.
当∠AOC=2∠AOB时,如图,
则:90-4t=2×40.
解得:t=,
当∠AOB=2∠AOC时,如图,
则:40=2(90-4t).
解得:t=,
综上,当射线OA是射线OB,OC的“双倍和谐线”时,t的值为或;
②由题意得:∠CON=4°t,∠AON=90°+2°t,∠AOD=20°,∠DON=∠AON-∠AOD=70°+2°t.
∵当射线OC与射线OA重合时,运动停止,
∴此时∠AON=∠CON.
∴90+2t=4t.
∴t=45.
∴当t=45秒时,运动停止,此时∠AON=180°.
∵射线OC位于射线OD左侧且射线OC是射线OM,OD的“双倍和谐线”,
∴∠COM=2∠COD或∠COD=2∠COM.
当∠COM=2∠COD时,如图,
即:180°-∠CON=2(∠CON-∠DON),
则:180-4t=2(4t-70-2t).
解得:t=40.
∴∠CON=4°×40=160°.
当∠COD=2∠COM时,如图,
即:∠CON-∠DON=2(180°-∠CON).
则:4t-(70+2t)=2(180-4t).
解得:t=43.
∴∠CON=4°×43=172°.
综上,当射线OC位于射线OD左侧且射线OC是射线OM,OD的“双倍和谐线”时,∠CON的度数为160°或172°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
