人教B版(2019)必修二 4.1.2 指数函数的性质与图像 课件(共40张PPT)
文档属性
| 名称 | 人教B版(2019)必修二 4.1.2 指数函数的性质与图像 课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 28.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-24 08:59:17 | ||
图片预览








文档简介
(共40张PPT)
数学组冲之
4.1.2指数函数的性质与图像
人教版高中数学B版必修第二册第四章第一节
情境引入
(1)一张纸,厚度为1,
将其对折1次,厚度变为_____,
将其对折两次,厚度变为_______,
将其对折三次,厚度变为_______,
将其对折次,厚度变为=_______;
(2)一张纸,面积为1,
将其对折1次,面积变为_____,
将其对折两次,面积变为_______,
将其对折三次,面积变为_______
将其对折次,面积=______
情境引入
2
4
8
【情境2】 考古学家经常利用碳14的含量来推断古生物死亡的大致时间。当有机体生存时,会持续不断地吸收碳14,从而其体内的碳14含量会保持在一定的水平;但当有机体死亡后,就会停止吸收碳14,其体内的碳14含量就会逐渐减少,而且每经过大约5730年后会变为原来的一半。
情境引入
【问题1】你能用函数表示有机体内的碳14含量y与其死亡时间之间的关系吗?
【问题2】一种已经死亡一万年的有机体,其体内的碳14含量是其存活时的百分之多少?
时间 x 5730年后 2个5730年后 3个5 730年后 ……
剩余量 y ……
假设某时刻有机体内碳14的含量为1,该有机体死亡年后
情境引入
【问题2】一种已经死亡一万年的有机体,其体内的碳14含量是其存活时的百分之多少?
【问题3】观察以上情境中这三个函数解析式,你能发现它们的共同特征吗?
=
【问题4】你能写出这一类函数的一般表达式吗?
一般地,函数 y=ax 称为指数函数,其中a是常数, a>0且a≠1.
概念形成
一、指数函数的定义
【活动1—捉迷藏】下面这些解析式中藏了两个指数函数.你能把它们找出来吗?
=
【问题6】你能总结出指数函数解析式的特征吗
【问题5】指数函数的定义中,为什么要规定a>0且a≠1
【活动2—我动手】
深入探究
x -2 -1 0 1 2
y=2x
二、指数函数的性质与图像
【活动2—我动手】
深入探究
x -2 -1 0 1 2
y=2x 1 2
4
【问题1】根据指数运算的定义,你能尝试得到指数函数y=2x的性质吗?
(1)定义域是 ;
(2)值域是 ;
(3)奇偶性是 ;
(4)单调性是 ;
【问题2】你能根据指数函数y=2x的性质,描述它的图像特征吗?
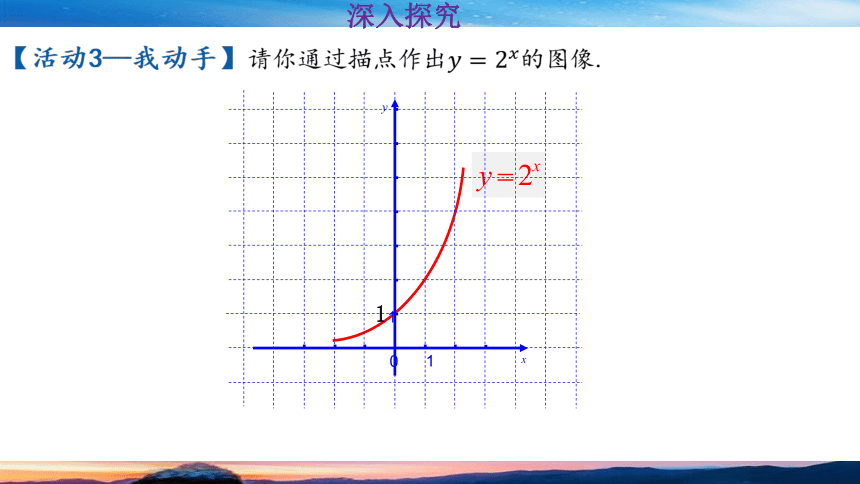
【活动3—我动手】请你通过描点作出的图像.
0
1
1
深入探究
1
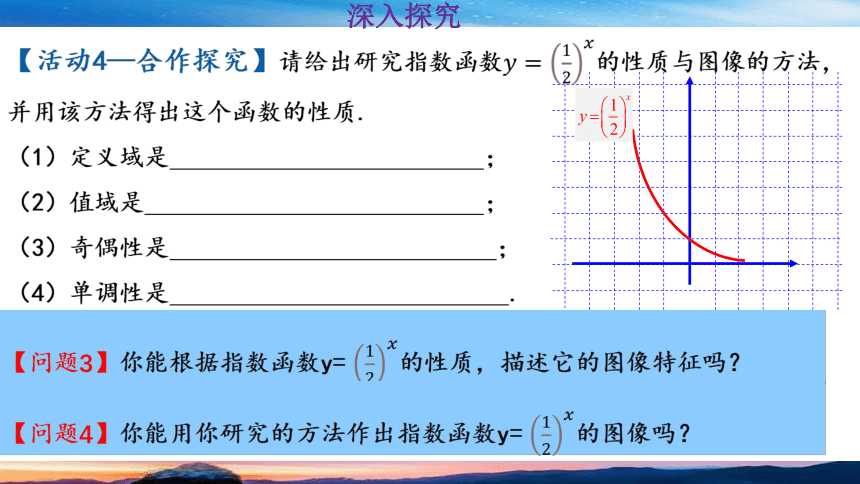
【活动4—合作探究】请给出研究指数函数的性质与图像的方法, 并用该方法得出这个函数的性质.
(1)定义域是 ;
(2)值域是 ;
(3)奇偶性是 ;
(4)单调性是 .
深入探究
【问题3】你能根据指数函数y= 的性质,描述它的图像特征吗?
【问题4】你能用你研究的方法作出指数函数y= 的图像吗?
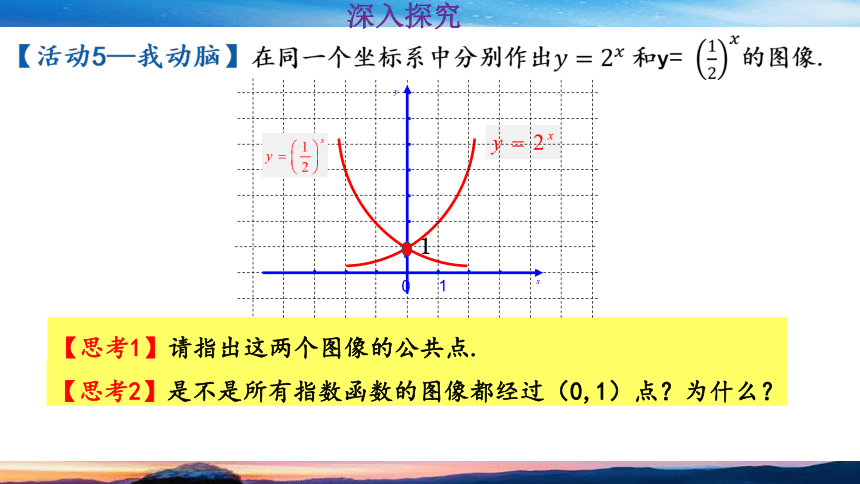
【活动5—我动脑】在同一个坐标系中分别作出和y= 的图像.
深入探究
【思考1】请指出这两个图像的公共点.
【思考2】是不是所有指数函数的图像都经过(0,1)点?为什么?
0
1
1
1
深入探究
0
1
1
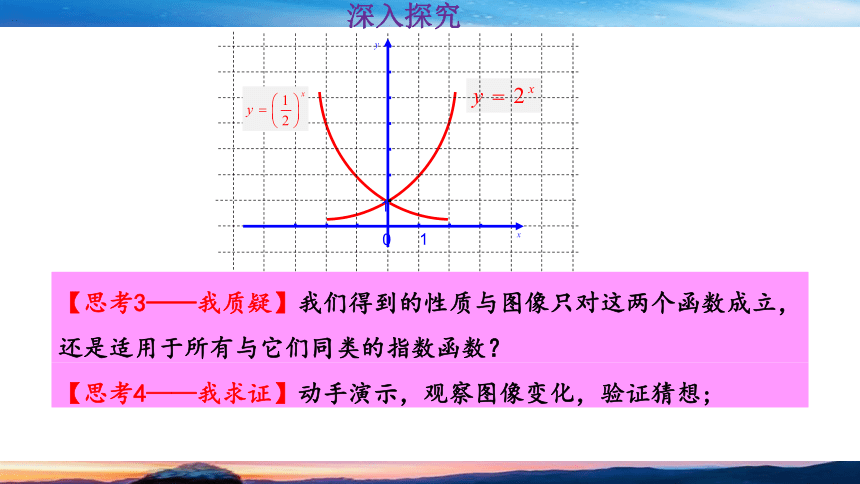
【思考3——我质疑】我们得到的性质与图像只对这两个函数成立,还是适用于所有与它们同类的指数函数?
【思考4——我求证】动手演示,观察图像变化,验证猜想;
深入探究
0
1
1
0
1
1
a>1 0图像
a>1 0图 像 特 征
a>1 0性 质
1.图像全在x轴上方,与x轴无限接近.
3.自左向右图像逐渐上升
3.自左向右图像逐渐下降
4.第一象限的图像在,
第二象限的图像在下方
4.第一象限的图像在,
第二象限的图像在方
5.图像既不关于x轴对称也不关于y轴对称
【活动6—我翻译】把图像的特征用数学语言翻译成对应的函数的性质.
深入探究
2.当x=0时,y=1
x
y
0
y=1
y=ax
(a>1)
(0,1)
y
0
(0x
y=1
y=ax
(0,1)
4.当x>0时,
当x<0时,
4.当x>0时,
当x<0时,
a>1 0图像
x
y
0
y=1
y=ax
(a>1)
(0,1)
y
0
(0x
y=1
y=ax
(0,1)
a>1 0图 像 特 征
a>1 0性 质
1.图像全在x轴上方,与x轴无限接近.
1.定义域为R,值域为(0,+ ).
2.图像过定点(0,1)
3.自左向右图像逐渐上升
3.自左向右图像逐渐下降
3.在R上是增函数
3.在R上是减函数
4.第一象限的图像在,
第二象限的图像在下方
4.第一象限的图像在,
第二象限的图像在方
4.当x>0时,y>1; 当x<0时,04.当x>0时,0当x<0时, y>1.
5.既不是奇函数又不是偶函数
5.图像既不关于x轴对称也不关于y轴对称
2.当x=0时,y=1
【活动6—我翻译】把图像的特征用数学语言翻译成对应的函数的性质.
深入探究
巩固应用
三、指数函数性质与图像的应用
例2.已知实数a,b满足 ,试判断6a与6b的大小.
巩固应用
【活动7—我攀登】
比较大小:
(1) (2)
【我提升】如何比较两个指数幂的大小?
同底不同指数: 利用指数函数的单调性比较大小
不同底不同指数: 先化成同底,再利用指数函数的单调性比较大小
这节课你学
到了什么?
知识
方法与思想
核心素养
归纳总结
指数函数的性质与图像
指数函数的概念
数学抽象
逻辑推理
由特殊到一般
数形结合
巅 峰 回 眸 豁 然 开 朗
分类讨论
直观想象
转化与化归
【活动10—我收获】请谈一谈你的收获。。。
【我的感悟】指数运算与生活哲学
勤学如春起之苗,
不见其增日有所长.
辍学如磨刀之石,
不见其损日有所亏.
---陶渊明
成长感悟
布置作业
作业一:课本13页练习A,练习B;
作业二:
(1)函数的单调性也可借助4.1.1中
(2)搜集生活中指数函数的实例,体会“指数爆炸效应”,感悟指数函数图像的变化趋势.
谢 谢 指 导
巩固应用
【活动7—我攀登】
比较大小:
(1) (2) (3)
【我提升】如何比较两个指数幂的大小?
同底不同指数: 利用指数函数的单调性比较大小
不同底不同指数:(1)化成同底;(2)找中间量
这节课你学
到了什么?
知识
方法与思想
核心素养
归纳总结
指数函数的性质与图像
指数函数的概念
数学抽象
逻辑推理
由特殊到一般
数形结合
巅 峰 回 眸 豁 然 开 朗
分类讨论
直观想象
转化与化归
【活动10—我收获】请谈一谈你的收获。。。
【我的感悟】指数运算与生活哲学
勤学如春起之苗,
不见其增日有所长.
辍学如磨刀之石,
不见其损日有所亏.
---陶渊明
成长感悟
布置作业
作业一:课本13页练习A,练习B;
作业二:
(1)函数的单调性也可借助4.1.1中
(2)搜集生活中指数函数的实例,体会“指数爆炸效应”,感悟指数函数图像的变化趋势.
谢 谢 指 导
情境引入
马王堆汉墓
美丽的辛追夫人被挖掘出时形态完整,皮肤保持弹性,部分关节还可以弯曲,这是人类历史上的一个奇迹。
1988年,科学家曾以碳14的半衰期测定其年代,结果震惊世界!
巩固应用
【活动9—我解决】签多少天的合同最划算?
解:设签天的合同
答:签16天的合同最划算.
32768 65536 131072 262144 524288
【活动5—我动脑】在同一个坐标系中分别作出和y= 的图像.
深入探究
【思考1——找相同】找一找这两个图像的相同之处有哪些?
【思考2——找不同】找一找这两个图像的不同之处有哪些?
【思考3——找联系】找一找这两个图像之间有什么联系?
0
1
1
1
【活动3—我动手】请你通过描点作出的图像.
0
1
1
【备注】函数的单调性也可借助 4.1.1中
深入探究
【情境1】假如有人要跟你签一份30天的合同,在这30天内,他每天给你100000块钱,你只需要第一天给他2块钱,第二天4块钱,第三天8块钱......你会不会签这张合同?
情境引入
天数 1 2 3 4 5 6 7 8 9 10 ……
付出的钱数 2 4 8 16 32 64 128 256 512 1024 ……
爆炸性增长(blow up)
30
1,073,741,824
【情境1】
(1)一张纸,厚度为1,将其对折1次,厚度变为_____,
将其对折两次,厚度变为_______,
将其对折次,厚度变为=_______;
(2)一张纸,面积为1,将其对折1次,面积变为_____,
将其对折两次,面积变为_______,
将其对折次,面积=_______;
情境引入
【情境2】 考古学家经常利用碳14的含量来推断古生物死亡的大致时间。当有机体生存时,会持续不断地吸收碳14,从而其体内的碳14含量会保持在一定的水平;但当有机体死亡后,就会停止吸收碳14,其体内的碳14含量就会逐渐减少,而且每经过大约5730年后会变为原来的一半。
情境引入
【问题1】你能用函数表示有机体内的碳14含量与其死亡时间之间的关系吗?
【问题2】一种已经死亡一万年的有机体,其体内的碳14含量是其存活时的百分之多少?
关系可表示为=_______
情境引入
【解决问题2】死亡一万年的有机体,其体内的碳14含量为 ______
是生存时的 。
定义理解
幂指数x为自变量,它的系数为1
底数a是不等于1 的正数
幂的系数为1
【小试身手】函数是指数函数,则
【活动2—我动手】
深入探究
x -2 -1 0 1 2
y=2x 1 2
4
【问题1】根据指数运算的定义,你能尝试得到指数函数y=2x的性质吗?
(1)定义域是 ;
(2)值域是 ;
(3)奇偶性是 ;
(4)单调性是 .
【问题2】你能根据指数函数y=2x的性质,描述它的图像特征吗?
向左向右无限延展.
图像都在x轴上方.
图像既不关于y轴对称,也不关于原点对称.
图像呈上升趋势.
【活动7—找朋友】请把左边的性质与右边它能解决的相应习题用直线连接.
巩固应用
性质
(1)定义域是实数集R.值域是(0,)
(2)函数图像一定过点(0,1).
(3)当a>1时,y=ax是R上的增函数;
当0应用
(1)比较大小:
(2)求函数定义域和值域.
(3)函数过什么
定点?
【活动7—找朋友】请把左边的性质与右边它能解决的相应习题用直线连接.
巩固应用
性质
(1)定义域是实数集R.值域是(0,)
(2)函数图像一定过点(0,1).
(3)当a>1时,y=ax是R上的增函数;
当0应用
(1)若不等式,则的取值范围是__
(2)求函数定义域和值域.
(3)函数过什么
定点?
x -2 -1 0 1 2
-x -2 -1 0 1
2
4 1
深入探究
课堂小结
【活动10—我收获】请谈一谈你的收获。。。
一、知识收获:
1.通过实际问题,了解指数函数的实际背景;
2.通过实例辨析,明确指数函数的概念和解析式特征;
3.能用由列表法猜测指数函数的性质,并由描点法画出指数函数的图象,验证猜想,归纳指数函数的性质;
4.能应用指数函数的图象与性质,解决简单的求定域和值域问题、定点问题,并会比较指数幂的大小.
二、素养达成:
1.通过指数函数概念的学习,培养了数学抽象素养;
2.借助指数函数性质与图像的学习,提升直观想象、逻辑推理素养.
数学组冲之
4.1.2指数函数的性质与图像
人教版高中数学B版必修第二册第四章第一节
情境引入
(1)一张纸,厚度为1,
将其对折1次,厚度变为_____,
将其对折两次,厚度变为_______,
将其对折三次,厚度变为_______,
将其对折次,厚度变为=_______;
(2)一张纸,面积为1,
将其对折1次,面积变为_____,
将其对折两次,面积变为_______,
将其对折三次,面积变为_______
将其对折次,面积=______
情境引入
2
4
8
【情境2】 考古学家经常利用碳14的含量来推断古生物死亡的大致时间。当有机体生存时,会持续不断地吸收碳14,从而其体内的碳14含量会保持在一定的水平;但当有机体死亡后,就会停止吸收碳14,其体内的碳14含量就会逐渐减少,而且每经过大约5730年后会变为原来的一半。
情境引入
【问题1】你能用函数表示有机体内的碳14含量y与其死亡时间之间的关系吗?
【问题2】一种已经死亡一万年的有机体,其体内的碳14含量是其存活时的百分之多少?
时间 x 5730年后 2个5730年后 3个5 730年后 ……
剩余量 y ……
假设某时刻有机体内碳14的含量为1,该有机体死亡年后
情境引入
【问题2】一种已经死亡一万年的有机体,其体内的碳14含量是其存活时的百分之多少?
【问题3】观察以上情境中这三个函数解析式,你能发现它们的共同特征吗?
=
【问题4】你能写出这一类函数的一般表达式吗?
一般地,函数 y=ax 称为指数函数,其中a是常数, a>0且a≠1.
概念形成
一、指数函数的定义
【活动1—捉迷藏】下面这些解析式中藏了两个指数函数.你能把它们找出来吗?
=
【问题6】你能总结出指数函数解析式的特征吗
【问题5】指数函数的定义中,为什么要规定a>0且a≠1
【活动2—我动手】
深入探究
x -2 -1 0 1 2
y=2x
二、指数函数的性质与图像
【活动2—我动手】
深入探究
x -2 -1 0 1 2
y=2x 1 2
4
【问题1】根据指数运算的定义,你能尝试得到指数函数y=2x的性质吗?
(1)定义域是 ;
(2)值域是 ;
(3)奇偶性是 ;
(4)单调性是 ;
【问题2】你能根据指数函数y=2x的性质,描述它的图像特征吗?
【活动3—我动手】请你通过描点作出的图像.
0
1
1
深入探究
1
【活动4—合作探究】请给出研究指数函数的性质与图像的方法, 并用该方法得出这个函数的性质.
(1)定义域是 ;
(2)值域是 ;
(3)奇偶性是 ;
(4)单调性是 .
深入探究
【问题3】你能根据指数函数y= 的性质,描述它的图像特征吗?
【问题4】你能用你研究的方法作出指数函数y= 的图像吗?
【活动5—我动脑】在同一个坐标系中分别作出和y= 的图像.
深入探究
【思考1】请指出这两个图像的公共点.
【思考2】是不是所有指数函数的图像都经过(0,1)点?为什么?
0
1
1
1
深入探究
0
1
1
【思考3——我质疑】我们得到的性质与图像只对这两个函数成立,还是适用于所有与它们同类的指数函数?
【思考4——我求证】动手演示,观察图像变化,验证猜想;
深入探究
0
1
1
0
1
1
a>1 0
a>1 0
a>1 0
1.图像全在x轴上方,与x轴无限接近.
3.自左向右图像逐渐上升
3.自左向右图像逐渐下降
4.第一象限的图像在,
第二象限的图像在下方
4.第一象限的图像在,
第二象限的图像在方
5.图像既不关于x轴对称也不关于y轴对称
【活动6—我翻译】把图像的特征用数学语言翻译成对应的函数的性质.
深入探究
2.当x=0时,y=1
x
y
0
y=1
y=ax
(a>1)
(0,1)
y
0
(0
y=1
y=ax
(0,1)
4.当x>0时,
当x<0时,
4.当x>0时,
当x<0时,
a>1 0
x
y
0
y=1
y=ax
(a>1)
(0,1)
y
0
(0
y=1
y=ax
(0,1)
a>1 0
a>1 0
1.图像全在x轴上方,与x轴无限接近.
1.定义域为R,值域为(0,+ ).
2.图像过定点(0,1)
3.自左向右图像逐渐上升
3.自左向右图像逐渐下降
3.在R上是增函数
3.在R上是减函数
4.第一象限的图像在,
第二象限的图像在下方
4.第一象限的图像在,
第二象限的图像在方
4.当x>0时,y>1; 当x<0时,0
5.既不是奇函数又不是偶函数
5.图像既不关于x轴对称也不关于y轴对称
2.当x=0时,y=1
【活动6—我翻译】把图像的特征用数学语言翻译成对应的函数的性质.
深入探究
巩固应用
三、指数函数性质与图像的应用
例2.已知实数a,b满足 ,试判断6a与6b的大小.
巩固应用
【活动7—我攀登】
比较大小:
(1) (2)
【我提升】如何比较两个指数幂的大小?
同底不同指数: 利用指数函数的单调性比较大小
不同底不同指数: 先化成同底,再利用指数函数的单调性比较大小
这节课你学
到了什么?
知识
方法与思想
核心素养
归纳总结
指数函数的性质与图像
指数函数的概念
数学抽象
逻辑推理
由特殊到一般
数形结合
巅 峰 回 眸 豁 然 开 朗
分类讨论
直观想象
转化与化归
【活动10—我收获】请谈一谈你的收获。。。
【我的感悟】指数运算与生活哲学
勤学如春起之苗,
不见其增日有所长.
辍学如磨刀之石,
不见其损日有所亏.
---陶渊明
成长感悟
布置作业
作业一:课本13页练习A,练习B;
作业二:
(1)函数的单调性也可借助4.1.1中
(2)搜集生活中指数函数的实例,体会“指数爆炸效应”,感悟指数函数图像的变化趋势.
谢 谢 指 导
巩固应用
【活动7—我攀登】
比较大小:
(1) (2) (3)
【我提升】如何比较两个指数幂的大小?
同底不同指数: 利用指数函数的单调性比较大小
不同底不同指数:(1)化成同底;(2)找中间量
这节课你学
到了什么?
知识
方法与思想
核心素养
归纳总结
指数函数的性质与图像
指数函数的概念
数学抽象
逻辑推理
由特殊到一般
数形结合
巅 峰 回 眸 豁 然 开 朗
分类讨论
直观想象
转化与化归
【活动10—我收获】请谈一谈你的收获。。。
【我的感悟】指数运算与生活哲学
勤学如春起之苗,
不见其增日有所长.
辍学如磨刀之石,
不见其损日有所亏.
---陶渊明
成长感悟
布置作业
作业一:课本13页练习A,练习B;
作业二:
(1)函数的单调性也可借助4.1.1中
(2)搜集生活中指数函数的实例,体会“指数爆炸效应”,感悟指数函数图像的变化趋势.
谢 谢 指 导
情境引入
马王堆汉墓
美丽的辛追夫人被挖掘出时形态完整,皮肤保持弹性,部分关节还可以弯曲,这是人类历史上的一个奇迹。
1988年,科学家曾以碳14的半衰期测定其年代,结果震惊世界!
巩固应用
【活动9—我解决】签多少天的合同最划算?
解:设签天的合同
答:签16天的合同最划算.
32768 65536 131072 262144 524288
【活动5—我动脑】在同一个坐标系中分别作出和y= 的图像.
深入探究
【思考1——找相同】找一找这两个图像的相同之处有哪些?
【思考2——找不同】找一找这两个图像的不同之处有哪些?
【思考3——找联系】找一找这两个图像之间有什么联系?
0
1
1
1
【活动3—我动手】请你通过描点作出的图像.
0
1
1
【备注】函数的单调性也可借助 4.1.1中
深入探究
【情境1】假如有人要跟你签一份30天的合同,在这30天内,他每天给你100000块钱,你只需要第一天给他2块钱,第二天4块钱,第三天8块钱......你会不会签这张合同?
情境引入
天数 1 2 3 4 5 6 7 8 9 10 ……
付出的钱数 2 4 8 16 32 64 128 256 512 1024 ……
爆炸性增长(blow up)
30
1,073,741,824
【情境1】
(1)一张纸,厚度为1,将其对折1次,厚度变为_____,
将其对折两次,厚度变为_______,
将其对折次,厚度变为=_______;
(2)一张纸,面积为1,将其对折1次,面积变为_____,
将其对折两次,面积变为_______,
将其对折次,面积=_______;
情境引入
【情境2】 考古学家经常利用碳14的含量来推断古生物死亡的大致时间。当有机体生存时,会持续不断地吸收碳14,从而其体内的碳14含量会保持在一定的水平;但当有机体死亡后,就会停止吸收碳14,其体内的碳14含量就会逐渐减少,而且每经过大约5730年后会变为原来的一半。
情境引入
【问题1】你能用函数表示有机体内的碳14含量与其死亡时间之间的关系吗?
【问题2】一种已经死亡一万年的有机体,其体内的碳14含量是其存活时的百分之多少?
关系可表示为=_______
情境引入
【解决问题2】死亡一万年的有机体,其体内的碳14含量为 ______
是生存时的 。
定义理解
幂指数x为自变量,它的系数为1
底数a是不等于1 的正数
幂的系数为1
【小试身手】函数是指数函数,则
【活动2—我动手】
深入探究
x -2 -1 0 1 2
y=2x 1 2
4
【问题1】根据指数运算的定义,你能尝试得到指数函数y=2x的性质吗?
(1)定义域是 ;
(2)值域是 ;
(3)奇偶性是 ;
(4)单调性是 .
【问题2】你能根据指数函数y=2x的性质,描述它的图像特征吗?
向左向右无限延展.
图像都在x轴上方.
图像既不关于y轴对称,也不关于原点对称.
图像呈上升趋势.
【活动7—找朋友】请把左边的性质与右边它能解决的相应习题用直线连接.
巩固应用
性质
(1)定义域是实数集R.值域是(0,)
(2)函数图像一定过点(0,1).
(3)当a>1时,y=ax是R上的增函数;
当0
(1)比较大小:
(2)求函数定义域和值域.
(3)函数过什么
定点?
【活动7—找朋友】请把左边的性质与右边它能解决的相应习题用直线连接.
巩固应用
性质
(1)定义域是实数集R.值域是(0,)
(2)函数图像一定过点(0,1).
(3)当a>1时,y=ax是R上的增函数;
当0
(1)若不等式,则的取值范围是__
(2)求函数定义域和值域.
(3)函数过什么
定点?
x -2 -1 0 1 2
-x -2 -1 0 1
2
4 1
深入探究
课堂小结
【活动10—我收获】请谈一谈你的收获。。。
一、知识收获:
1.通过实际问题,了解指数函数的实际背景;
2.通过实例辨析,明确指数函数的概念和解析式特征;
3.能用由列表法猜测指数函数的性质,并由描点法画出指数函数的图象,验证猜想,归纳指数函数的性质;
4.能应用指数函数的图象与性质,解决简单的求定域和值域问题、定点问题,并会比较指数幂的大小.
二、素养达成:
1.通过指数函数概念的学习,培养了数学抽象素养;
2.借助指数函数性质与图像的学习,提升直观想象、逻辑推理素养.
