人教B版(2019)必修二 4.1.2 指数函数的性质与图像 课件(共24张PPT)
文档属性
| 名称 | 人教B版(2019)必修二 4.1.2 指数函数的性质与图像 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-24 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
指数函数性质及图像
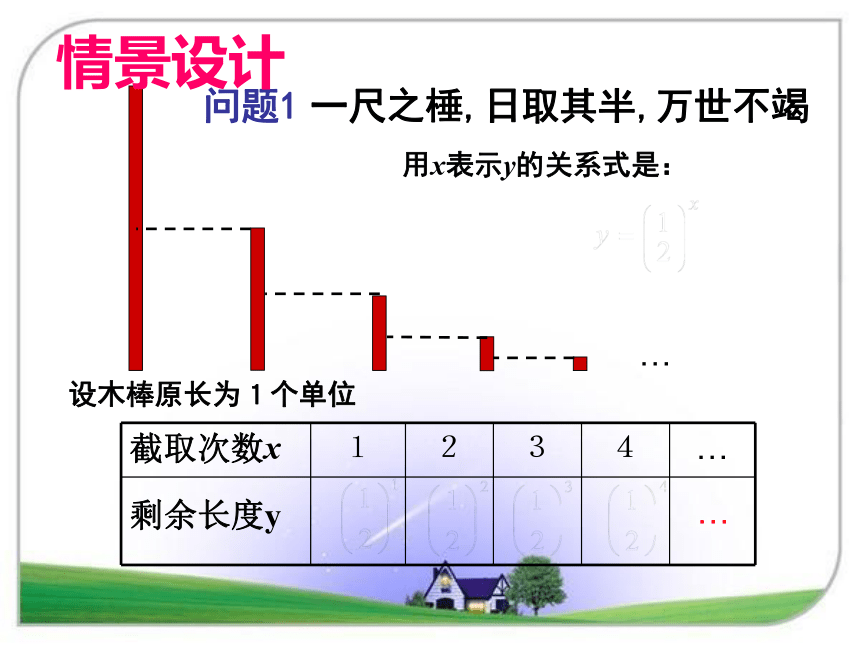
问题1 一尺之棰,日取其半,万世不竭
设木棒原长为1个单位
…
用x表示y的关系式是:
截取次数x
1
2
3
4
…
剩余长度y
…
情景设计
1.等式特点:
2.自变量位置:
3.底数情况:
解析式是指数式的形式
指数部分仅有自变量 x,
且幂式的整体系数为 1
底数是正实数
这两个解析式的形式有什么共同特征?
思考1
情景设计
问题2 细胞分裂问题
…………
…………
…………
…………
分裂次数x 1 2 3 4 …
细胞个数y
…
用x表示y的关系式是:
一般的,函数 称为指数
函数,其中a是常数, a >0且a ≠1.
指数函数的概念
①底数:大于零且不等于1的常数;
②指数:仅自变量x;
③幂式系数:1.
为什么要规定a>0,且 a≠1呢?
①若a=1,
②若 ,
思考2
则对于任何
是一个常量,没有研究的价值.
无意义.
③若 ,
练习:
1.下列函数是指数函数的是 ( )
A. y=(-3)x B. y=3x+1 C. y=-3x+1 D. y=3-x
2.函数 y = ( a2 - 3a + 3) ax 是指数函数,求 a的值.
解:由指数函数 的定义有
a2 - 3a + 3=1
a>0
a ≠ 1
∴ a = 2
a =1或a = 2
a>0
a≠1
解得
D
数缺形时少直观
形缺数时难入微
数形结合百般好
隔离分家万事休
——华罗庚
思考:
研究函数性质一般从哪些方面去研究?
2.指数函数的性质和图像
定义域、值域、单调性、奇偶性
分别求指数函数 在自变量取-2,-1, ,0, ,1,2时所对应的函数值,请同学们填写以下表格,并根据所填数值猜想指数函数 的定义域、值域、奇偶性、单调性.
x -2 -1 0 1 2
y=2x
探究一:对指数函数 的探究
探究二:对指数函数 的探究
请同学们在直角坐标系中画出指数函数 的图像,并从图像中观察函数有哪些性质?
思考:画函数图像的方法和步骤步骤是什么?
分别求指数函数 在自变量取-2,-1, ,0, ,1,2时所对应的函数值,请同学们填写以下表格,并根据所填数值猜想指数函数 的定义域、值域、奇偶性、单调性.
x -2 -1 0 1 2
y=2x
定义域: ________
值域: ________
奇偶性: ________
单调性: ________
探究一:对指数函数 的探究
-4
-3
-2
-1
0
1
1
2
2
3
4
3
4
0
1
1
-1
-3
-2
2
3
定义域:________
值域: ________
奇偶性:________
单调性:________
2
3
4
5
6
… -2 -1 0 1 2 …
… 4 2 1 …
0
1
1
思考:1.你能指出这两个函数的相同点与不同点吗?
2.你能得出指数函数 的性质吗?
图像
0
1
1
0
1
1
0
1
0
1
图像变化
y
x
0
· (0,1)
指数函数 的图像和性质
1. 定义域:
2. 值 域:
3. 定 点:
4. 单调性:
5. 函数值的变化情况:
当 x < 0时, 0< y <1.
R ;
( 0 , +∞) ;
( 0 , 1) ;
在 R 上是增函数;
当 x > 0时, y > 1.
a>1 0(5)奇偶性:
y
x
0
y=1
(0,1)
y=ax
(a>1)
x
(0,1)
y=1
0
y=ax
(0R
( 0 , + ∞ )
( 0 , 1 )
0
1
增
减
非奇非偶函数
当 x > 0 时,y > 1;
当 x < 0 时, 0< y < 1.
当 x < 0 时,y > 1;
当 x > 0 时, 0< y < 1.
思考4
类比 指数函数的性质得 时的性质?
例1:比较下列各题中两值的大小
方法总结:
对同底数幂大小的比较用的是指数函数的单调性,必须要明确所给的两个值是哪个指数函数的两个函数值;
<
<
答案:分 a>1 和 0当 a>1 时, a3 < a4;
当 0 a4.
(3)比较a3 与 a4 (a>0且a≠1)的大小
解:
以1为中 间值
3.当底数不同不能直接比较时:可借助中间
数(如1或0等),间接比较两个指数的大小.
总结:
1.当同底数并明确底数a与1的大小关系时:
直接用函数的单调性来解;
2.当同底数但不明确底数a与1的大小关系时: 要分情况讨论;
比较下列各题中两个数的大小:
(1)
(2)
(3)
<
>
>
课堂小结
1 指数函数的概念;
2 指数函数的图像和性质;
3 数学思想:
数形结合、分类讨论、由特殊到一般.
勤学如初见之苗,不见其增,日有所长;
辍学如磨刀之石,不见其损,日有所亏.
课后作业
1.必做题:13页练习A、B第1、2题
2.选做题:
从数和形两个角度研究函数 与 的图像的关系,并利用函数 的图像,在同一坐标系中做出 的草图.
3.课后思考题:解不等式
祝同学们学习进步!
再见!
指数函数性质及图像
问题1 一尺之棰,日取其半,万世不竭
设木棒原长为1个单位
…
用x表示y的关系式是:
截取次数x
1
2
3
4
…
剩余长度y
…
情景设计
1.等式特点:
2.自变量位置:
3.底数情况:
解析式是指数式的形式
指数部分仅有自变量 x,
且幂式的整体系数为 1
底数是正实数
这两个解析式的形式有什么共同特征?
思考1
情景设计
问题2 细胞分裂问题
…………
…………
…………
…………
分裂次数x 1 2 3 4 …
细胞个数y
…
用x表示y的关系式是:
一般的,函数 称为指数
函数,其中a是常数, a >0且a ≠1.
指数函数的概念
①底数:大于零且不等于1的常数;
②指数:仅自变量x;
③幂式系数:1.
为什么要规定a>0,且 a≠1呢?
①若a=1,
②若 ,
思考2
则对于任何
是一个常量,没有研究的价值.
无意义.
③若 ,
练习:
1.下列函数是指数函数的是 ( )
A. y=(-3)x B. y=3x+1 C. y=-3x+1 D. y=3-x
2.函数 y = ( a2 - 3a + 3) ax 是指数函数,求 a的值.
解:由指数函数 的定义有
a2 - 3a + 3=1
a>0
a ≠ 1
∴ a = 2
a =1或a = 2
a>0
a≠1
解得
D
数缺形时少直观
形缺数时难入微
数形结合百般好
隔离分家万事休
——华罗庚
思考:
研究函数性质一般从哪些方面去研究?
2.指数函数的性质和图像
定义域、值域、单调性、奇偶性
分别求指数函数 在自变量取-2,-1, ,0, ,1,2时所对应的函数值,请同学们填写以下表格,并根据所填数值猜想指数函数 的定义域、值域、奇偶性、单调性.
x -2 -1 0 1 2
y=2x
探究一:对指数函数 的探究
探究二:对指数函数 的探究
请同学们在直角坐标系中画出指数函数 的图像,并从图像中观察函数有哪些性质?
思考:画函数图像的方法和步骤步骤是什么?
分别求指数函数 在自变量取-2,-1, ,0, ,1,2时所对应的函数值,请同学们填写以下表格,并根据所填数值猜想指数函数 的定义域、值域、奇偶性、单调性.
x -2 -1 0 1 2
y=2x
定义域: ________
值域: ________
奇偶性: ________
单调性: ________
探究一:对指数函数 的探究
-4
-3
-2
-1
0
1
1
2
2
3
4
3
4
0
1
1
-1
-3
-2
2
3
定义域:________
值域: ________
奇偶性:________
单调性:________
2
3
4
5
6
… -2 -1 0 1 2 …
… 4 2 1 …
0
1
1
思考:1.你能指出这两个函数的相同点与不同点吗?
2.你能得出指数函数 的性质吗?
图像
0
1
1
0
1
1
0
1
0
1
图像变化
y
x
0
· (0,1)
指数函数 的图像和性质
1. 定义域:
2. 值 域:
3. 定 点:
4. 单调性:
5. 函数值的变化情况:
当 x < 0时, 0< y <1.
R ;
( 0 , +∞) ;
( 0 , 1) ;
在 R 上是增函数;
当 x > 0时, y > 1.
a>1 0
y
x
0
y=1
(0,1)
y=ax
(a>1)
x
(0,1)
y=1
0
y=ax
(0
( 0 , + ∞ )
( 0 , 1 )
0
1
增
减
非奇非偶函数
当 x > 0 时,y > 1;
当 x < 0 时, 0< y < 1.
当 x < 0 时,y > 1;
当 x > 0 时, 0< y < 1.
思考4
类比 指数函数的性质得 时的性质?
例1:比较下列各题中两值的大小
方法总结:
对同底数幂大小的比较用的是指数函数的单调性,必须要明确所给的两个值是哪个指数函数的两个函数值;
<
<
答案:分 a>1 和 0
当 0
(3)比较a3 与 a4 (a>0且a≠1)的大小
解:
以1为中 间值
3.当底数不同不能直接比较时:可借助中间
数(如1或0等),间接比较两个指数的大小.
总结:
1.当同底数并明确底数a与1的大小关系时:
直接用函数的单调性来解;
2.当同底数但不明确底数a与1的大小关系时: 要分情况讨论;
比较下列各题中两个数的大小:
(1)
(2)
(3)
<
>
>
课堂小结
1 指数函数的概念;
2 指数函数的图像和性质;
3 数学思想:
数形结合、分类讨论、由特殊到一般.
勤学如初见之苗,不见其增,日有所长;
辍学如磨刀之石,不见其损,日有所亏.
课后作业
1.必做题:13页练习A、B第1、2题
2.选做题:
从数和形两个角度研究函数 与 的图像的关系,并利用函数 的图像,在同一坐标系中做出 的草图.
3.课后思考题:解不等式
祝同学们学习进步!
再见!
