人教B版必修2第四章4.1.1实数指数幂的运算讲课 课件(共38张PPT)
文档属性
| 名称 | 人教B版必修2第四章4.1.1实数指数幂的运算讲课 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-24 00:00:00 | ||
图片预览











文档简介
(共38张PPT)
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
新冠病毒颗粒呈圆形或者椭圆形,直径平均
100纳米,肉眼是看不到的。而大家看到的是被科学家
放大十万倍后的新冠病毒。已知1纳米等于十亿分之一米。
,你能算出放大十万倍后病毒的直径近似几厘米吗
新型冠状病毒
创设情境,引入新知
整数指数幂的运算
创设情境,引入新知
创设情境,引入新知
实数指数幂及其运算
人教B版必修2第四章4.1.1
a的n次幂
底数
指数
规定:
复习回顾,温故知新
整数指数幂的运算法则
n次方根如何定义呢?
新知1:n次方根的定义
一般地,给定大于1的正整数n和实数
如果存在实数 ,使得
(或二次方根)
(或三次方根)
新知2:n次方根的性质
注:
1.正数的平方根有两个,
它们互为相反数;
零的平方根是零;
负数没有平方根.
2.任意实数的立方根
都只有一个.
新知2:n次方根的性质
新知2:n次方根的性质
1. 正数的偶数次方根有两个,且是相反数,分别表示为:
正的方根称为 的 次算术根,记作
0的偶数次方根是0,
负数没有偶数次方根,
2.任意实数的奇数次方根都只有一个.表示为:
正数的奇数次方根是一个正数,
负数的奇数次方根是一个负数.
根指数
根式
被开方数
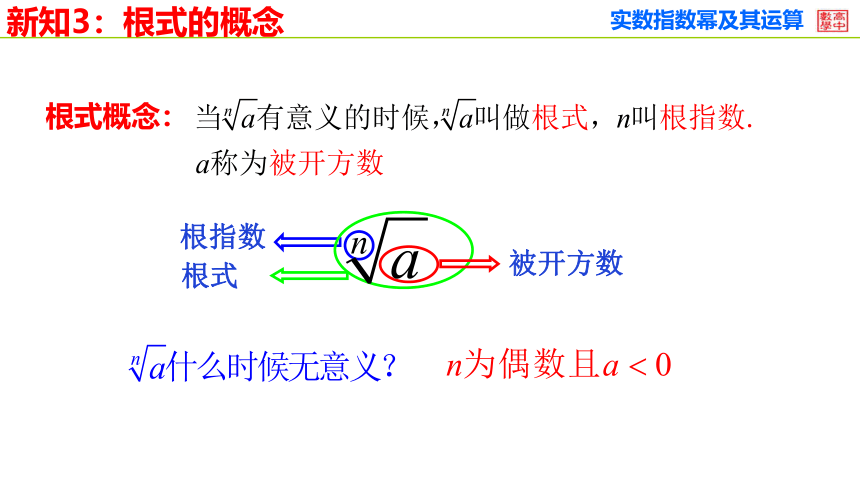
根式概念:
新知3:根式的概念
探究2:
探究3:
新知4:根式的性质
根式的
性质1
根式的
性质2
根式的性质:
1
请牢记:
我们不一样
小试牛刀
新知4:根式的性质
要有意义哦!!!
探究4:根式能不能转化成幂的形式?
观察以上式子,幂中的分数指数的分子、分母与根式中被开方数的指数、根指数,你能得出怎样的关系?
根式可以写成分数作为指数的形式(分数指数幂形式).
探究4:根式能不能转化成幂的形式?
正分数指数幂定义为:
①根指数 分数指数的分母
②被开方数(式)的指数 分数指数的分子
化为
化为
新知5:分数指数幂
负分数指数幂
规定:0的正分数指数幂等于0.
0的负分数指数幂无意义.
分数指数幂的底数不一定为正数.
1.用根式表示下列各式
2.根式化成分数指数幂的形式
【小试牛刀】
【方法技巧】根式与分数指数幂互化的规律
③负分数指数幂写成正分数指数幂的倒数
①根指数 分数指数的分母
②被开方数(式)的指数 分数指数的分子
化为
化为
有理数指数幂的运算法则:
有理指数幂
新知6:有理数指数幂
根据不等式的性质与根式的性质,得
或
证明: 假设
即 或
这都与 矛盾,因此假设不成立,从而
例1. 求证:如果 ,n是大于1的自然数,那么
2. 如果 ,s是正有理数,那么
1. 如果 ,s是正有理数,那么
3. 如果 , ,且s与t均为有理数,那么
由例1的结论又可以得到以下结论
典例分析,学以致用
猜测2π与23的相对大小,以及2π与24的相对大小
3.1<π<3.2, 23.1<2π<23.2,
3.14<π<3.15 23.14<2π<23.15
3.141<π<3.142 23.141<2π<23.142
3.1415<π<3.1416 23.1415<2π<23.1416
3.14159<π<3.14160 23.14159<2π<23.14160
也就是说,两个序列
3.1,3.14,3.141,3.1415,3.14159,...;
3.2.,3.15,3.142,3.1416,3.14160,...
中的数,随着小数点后位数的增加,都越来越接近π,从而两个序列
23.1,23.14,23.141,23.1415,23.14159,...;
23.2,23.15,23.142,23.1416,23.14160,...;
中的数,随着指数的变化,也都会越来越接近一个实数,这个实数就是2π
无理指数幂
无理指数幂 (a>0,t是无理数)是一个确定的_____,
有理指数幂的运算性质对于无理指数幂_________.
实数
同样适用
新知7:无理数指数幂
3.1
3.2
π
23.1
23.2
2π
实数指数幂的运算法则:
新知8:实数指数幂
例2.计算下列各式的值
典例分析,学以致用
例3.化简
典例分析,学以致用
跟踪练习,强化训练
练习:化简下列各式
课堂小结:
2.方法层面
1.知识层面
(1)n次方根的定义、根式定义及根式性质;
(2)根式与分数指数幂的转化;
类比思想、
由特殊到一般的思想方法、
分类讨论、
转化思想
(3)有理指数幂、实数指数幂的运算性质。
数学运算 、数学抽象
3.核心素养
基础作业:练习A
练习B第1题
发展作业:B组第2题第3题
作业:
1.把分数指数幂写成根式形式:
(1) =_______;(2) =_______;(3) =_______.
2.把根式写成分数指数幂形式:
(1)
(2)
【小试牛刀】
新知2:n次方根的性质
2. 正数的偶次方根
结论:
3.任意实数的奇数次方根都只有一个.
1. 0的任意正整数次方根
均为0,记作:
有两个,且是相反数,分别表示为:
负数没有偶次方根,正的方根称为 的 次算术根,记作
正数的奇次方根是一个正数,
负数的奇次方根是一个负数.
表示为:
读作:n次根号
新知2:n次方根的性质
新知2:n次方根的性质
正分数指数幂定义为:
【思考】
你能否类比负整数指数幂定义给负分数指数幂下个定义?
①根指数 分数指数的分母
②被开方数(式)的指数 分数指数的分子
化为
化为
新知5:分数指数幂
新知2:n次方根的性质
2. 正数的偶次方根
结论:
3.任意实数的奇数次方根都只有一个.
1. 0的任意正整数次方根
均为0,记作:
有两个,且是相反数,分别表示为:
负数没有偶次方根,正的方根称为 的 次算术根,记作
正数的奇次方根是一个正数,
负数的奇次方根是一个负数.
表示为:
读作:n次根号
新知2:n次方根的性质
本节收获:
2.方法层面
1.知识层面
数学运算 、数学抽象
(1)n次方根的定义、根式定义及根式性质;
(2)根式与分数指数幂的转化;
类比思想、
由特殊到一般的思想方法、
转化思想
3.核心素养
(3)有理指数幂、实数指数幂的运算性质。
分类讨论
猜测2π与23的相对大小,以及2π与24的相对大小
3.1<π<3.2, 23.1<2π<23.2,
3.14<π<3.15 23.14<2π<23.15
3.141<π<3.142 23.141<2π<23.142
3.1415<π<3.1416 23.1415<2π<23.1416
3.14159<π<3.14160 23.14159<2π<23.14160
也就是说,两个序列
3.1,3.14,3.141,3.1415,3.14159,...;
3.2.,3.15,3.142,3.1416,3.14160,...
中的数,随着小数点后位数的增加,都越来越接近,从而两个序列
23.1,23.14,23.141,23.1415,23.14159,...;
23.2,23.15,23.142,23.1416,23.14160,...;
中的数,随着指数的变化,也都会越来越接近一个实数,这个实数就是2π
无理指数幂
无理指数幂 (a>0,t是无理数)是一个确定的_____,
有理指数幂的运算性质对于无理指数幂_________.
实数
同样适用
新知7:无理数指数幂
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
新冠病毒颗粒呈圆形或者椭圆形,直径平均
100纳米,肉眼是看不到的。而大家看到的是被科学家
放大十万倍后的新冠病毒。已知1纳米等于十亿分之一米。
,你能算出放大十万倍后病毒的直径近似几厘米吗
新型冠状病毒
创设情境,引入新知
整数指数幂的运算
创设情境,引入新知
创设情境,引入新知
实数指数幂及其运算
人教B版必修2第四章4.1.1
a的n次幂
底数
指数
规定:
复习回顾,温故知新
整数指数幂的运算法则
n次方根如何定义呢?
新知1:n次方根的定义
一般地,给定大于1的正整数n和实数
如果存在实数 ,使得
(或二次方根)
(或三次方根)
新知2:n次方根的性质
注:
1.正数的平方根有两个,
它们互为相反数;
零的平方根是零;
负数没有平方根.
2.任意实数的立方根
都只有一个.
新知2:n次方根的性质
新知2:n次方根的性质
1. 正数的偶数次方根有两个,且是相反数,分别表示为:
正的方根称为 的 次算术根,记作
0的偶数次方根是0,
负数没有偶数次方根,
2.任意实数的奇数次方根都只有一个.表示为:
正数的奇数次方根是一个正数,
负数的奇数次方根是一个负数.
根指数
根式
被开方数
根式概念:
新知3:根式的概念
探究2:
探究3:
新知4:根式的性质
根式的
性质1
根式的
性质2
根式的性质:
1
请牢记:
我们不一样
小试牛刀
新知4:根式的性质
要有意义哦!!!
探究4:根式能不能转化成幂的形式?
观察以上式子,幂中的分数指数的分子、分母与根式中被开方数的指数、根指数,你能得出怎样的关系?
根式可以写成分数作为指数的形式(分数指数幂形式).
探究4:根式能不能转化成幂的形式?
正分数指数幂定义为:
①根指数 分数指数的分母
②被开方数(式)的指数 分数指数的分子
化为
化为
新知5:分数指数幂
负分数指数幂
规定:0的正分数指数幂等于0.
0的负分数指数幂无意义.
分数指数幂的底数不一定为正数.
1.用根式表示下列各式
2.根式化成分数指数幂的形式
【小试牛刀】
【方法技巧】根式与分数指数幂互化的规律
③负分数指数幂写成正分数指数幂的倒数
①根指数 分数指数的分母
②被开方数(式)的指数 分数指数的分子
化为
化为
有理数指数幂的运算法则:
有理指数幂
新知6:有理数指数幂
根据不等式的性质与根式的性质,得
或
证明: 假设
即 或
这都与 矛盾,因此假设不成立,从而
例1. 求证:如果 ,n是大于1的自然数,那么
2. 如果 ,s是正有理数,那么
1. 如果 ,s是正有理数,那么
3. 如果 , ,且s与t均为有理数,那么
由例1的结论又可以得到以下结论
典例分析,学以致用
猜测2π与23的相对大小,以及2π与24的相对大小
3.1<π<3.2, 23.1<2π<23.2,
3.14<π<3.15 23.14<2π<23.15
3.141<π<3.142 23.141<2π<23.142
3.1415<π<3.1416 23.1415<2π<23.1416
3.14159<π<3.14160 23.14159<2π<23.14160
也就是说,两个序列
3.1,3.14,3.141,3.1415,3.14159,...;
3.2.,3.15,3.142,3.1416,3.14160,...
中的数,随着小数点后位数的增加,都越来越接近π,从而两个序列
23.1,23.14,23.141,23.1415,23.14159,...;
23.2,23.15,23.142,23.1416,23.14160,...;
中的数,随着指数的变化,也都会越来越接近一个实数,这个实数就是2π
无理指数幂
无理指数幂 (a>0,t是无理数)是一个确定的_____,
有理指数幂的运算性质对于无理指数幂_________.
实数
同样适用
新知7:无理数指数幂
3.1
3.2
π
23.1
23.2
2π
实数指数幂的运算法则:
新知8:实数指数幂
例2.计算下列各式的值
典例分析,学以致用
例3.化简
典例分析,学以致用
跟踪练习,强化训练
练习:化简下列各式
课堂小结:
2.方法层面
1.知识层面
(1)n次方根的定义、根式定义及根式性质;
(2)根式与分数指数幂的转化;
类比思想、
由特殊到一般的思想方法、
分类讨论、
转化思想
(3)有理指数幂、实数指数幂的运算性质。
数学运算 、数学抽象
3.核心素养
基础作业:练习A
练习B第1题
发展作业:B组第2题第3题
作业:
1.把分数指数幂写成根式形式:
(1) =_______;(2) =_______;(3) =_______.
2.把根式写成分数指数幂形式:
(1)
(2)
【小试牛刀】
新知2:n次方根的性质
2. 正数的偶次方根
结论:
3.任意实数的奇数次方根都只有一个.
1. 0的任意正整数次方根
均为0,记作:
有两个,且是相反数,分别表示为:
负数没有偶次方根,正的方根称为 的 次算术根,记作
正数的奇次方根是一个正数,
负数的奇次方根是一个负数.
表示为:
读作:n次根号
新知2:n次方根的性质
新知2:n次方根的性质
正分数指数幂定义为:
【思考】
你能否类比负整数指数幂定义给负分数指数幂下个定义?
①根指数 分数指数的分母
②被开方数(式)的指数 分数指数的分子
化为
化为
新知5:分数指数幂
新知2:n次方根的性质
2. 正数的偶次方根
结论:
3.任意实数的奇数次方根都只有一个.
1. 0的任意正整数次方根
均为0,记作:
有两个,且是相反数,分别表示为:
负数没有偶次方根,正的方根称为 的 次算术根,记作
正数的奇次方根是一个正数,
负数的奇次方根是一个负数.
表示为:
读作:n次根号
新知2:n次方根的性质
本节收获:
2.方法层面
1.知识层面
数学运算 、数学抽象
(1)n次方根的定义、根式定义及根式性质;
(2)根式与分数指数幂的转化;
类比思想、
由特殊到一般的思想方法、
转化思想
3.核心素养
(3)有理指数幂、实数指数幂的运算性质。
分类讨论
猜测2π与23的相对大小,以及2π与24的相对大小
3.1<π<3.2, 23.1<2π<23.2,
3.14<π<3.15 23.14<2π<23.15
3.141<π<3.142 23.141<2π<23.142
3.1415<π<3.1416 23.1415<2π<23.1416
3.14159<π<3.14160 23.14159<2π<23.14160
也就是说,两个序列
3.1,3.14,3.141,3.1415,3.14159,...;
3.2.,3.15,3.142,3.1416,3.14160,...
中的数,随着小数点后位数的增加,都越来越接近,从而两个序列
23.1,23.14,23.141,23.1415,23.14159,...;
23.2,23.15,23.142,23.1416,23.14160,...;
中的数,随着指数的变化,也都会越来越接近一个实数,这个实数就是2π
无理指数幂
无理指数幂 (a>0,t是无理数)是一个确定的_____,
有理指数幂的运算性质对于无理指数幂_________.
实数
同样适用
新知7:无理数指数幂
