4.1.1实数指数幂及其运算 课件(共27张PPT)
文档属性
| 名称 | 4.1.1实数指数幂及其运算 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 386.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-24 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
2
Loading
4.1.1 实数指数幂及其运算
人教版高中数学B版必修第二册
励志公式:
①:
1.01
1.01
1.01
……
=
1.01
365
≈
37.78
>
1
②:
0.99
0.99
0.99
……
=
0.99
365
≈
0.03
<
1
数学告诉我们,积跬步以至千里,积怠惰以至深渊
情景引入
情景引入
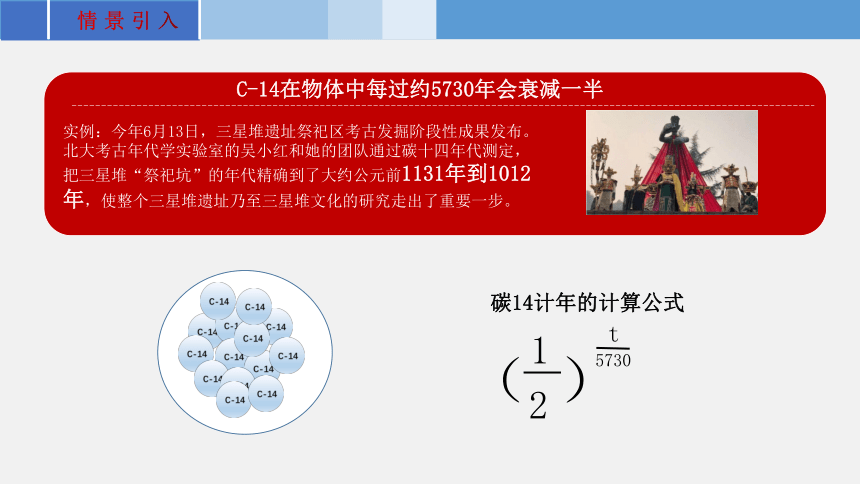
实例:今年6月13日,三星堆遗址祭祀区考古发掘阶段性成果发布。北大考古年代学实验室的吴小红和她的团队通过碳十四年代测定,把三星堆“祭祀坑”的年代精确到了大约公元前1131年到1012年,使整个三星堆遗址乃至三星堆文化的研究走出了重要一步。
C-14在物体中每过约5730年会衰减一半
碳14计年的计算公式
( )
1
2
t
5730
复习回顾
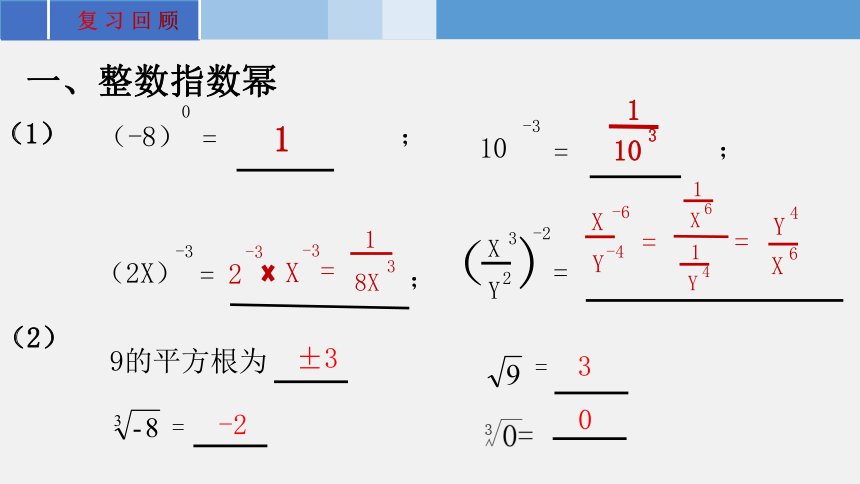
一、整数指数幂
1
(-8)
0
=
;
10
3
1
2
-3
X
-3
=
8X
3
1
Y
-4
X
-6
=
Y
4
1
X
6
1
=
Y
6
X
4
10
-3
=
;
(2X)
-3
=
;
(
Y
2
X
3
-2
)
=
.
(1)
(2)
9的平方根为
=
=
±3
3
-2
0
与探究任务一
类比二次方根与三次方根,能否给出四次方根和五次方根的定义?
(1)若x =a,则称x为a的四次方根
4
I)当a=0时,a的四次方方根只有一个0,记作 0=0;
II)当a>0时,a有两个四次方根,他们互为相反数,正的四次方根为 a,负的四次方根为- a;
II)当a<0时,在实数范围内没有四次方根。
4
4
4
(2)若x =a,则称x为a的五次方根
5
在实数范围内,任意实数a有且只有一个五次方根,记为 a
5
探究新知
概念形成
二、分数指数幂:
0
1.a的n次方根
一般地,给定大于1的正整数n和实数a,如果存在实数x,使得x =a,则x称为a的n次方根。
n
①: 0=
②:n为偶数:当a>0时:a有两个n次方根为± a ,其中 a 为n次算术根;当a<0时: a 在实数范围内无意义。
n为奇数:a有唯一n次方根 a
2.性质
n
n
n
n
概念形成
2. 根式:
(1)定义:当 有意义的时候, 称为根式,读作“n次根号a”
n
a
n
a
根指数
被开方数
n
a
n
a
何时 有意义时? 的意义是什么呢?
概念深化
(2)根式的性质:
I):
II):当n为奇数时, ;当n为偶数时:
n
( )
a
n
=a
n
a
n
=a
n
n
a
=|a|
性质应用
例1 化简下列各式
(1)
(4)
(2)
(3)
(6)
(5)
尝试与发现
探究任务二
第一组任务:
1.当a>0时,计算 是多少?
5
a
10
2.观察计算结果的指数与a的指数10和根指数5有什么等量关系?
3.能否将 写成分数为指数的幂的形式?
5
10
第二组任务:
1.当a>0时,计算 是多少?
4
a
12
2.观察计算结果的指数与a的指数12和根指数4是否有等量关系?
3.能否将 写成分数为指数的幂的形式?
4
a
12
尝试与发现
5
a
10
=
5
(a)
2
5
=
a
2
=
a
5
10
(a>0)
进一步观察:
4
a
12
=
4
(a )
3
4
=
a
3
=
a
4
12
(a>0)
( )
( )
概念形成
3.分数指数幂
(1)为了方便,我们约定a>0,规定 (n∈N )
a
n
1
=
a
n
*
5
4
3
=
=
(5 )
3
4
1
=
5
4
3
3
(2)对于 m,n∈N 且 为既约分数,规定:
*
m
n
a
n
m
=
a
n
m
=
a
n
m
例如:
a
n
m
-
=
a
n
m
1
1
=
a
n
m
注意m,n的位置
( )
5
4
概念深化
发现
说明:①:只要根式 有意义, ,不一定非得a>0.
a
n
a
n
a
n
1
=
比如:
-8
3
=
(-8)
3
1
②:
(-8)
6
2
=
-8
6
2
但是, 没有意义,
-8
( )
6
2
这样,我们就将整数指数幂推广到了分数指数幂,即有理数指数幂。
(-8)
6
1
2
( )
=
( )
一般地,没有特殊说明,认为分数中指数幂中指数都是既约分数
概念深化
4.有理数指数幂运算法则:
( )
当s与t都是有理数时,有运算法则:
s
a
a
t
=
a
S+t
s
a
t
=
a
St
( )
ab
s
=
a
S
b
S
练一练:
自主阅读课本P6部分并作答
7
练一练
练一练
( )
8
3
1
2
=
2
2
=
4
( )
a
3
2
3
( )
b
4
1
3
=
a
2
3
3
2
1
3
3
1
3
6
1
=
3
2
=
9
①
②
③
探究新知
我们写不出 的精确的小数形式,但是3.1<π<3.2
2
π
得:
2
3.1
<
2
π
<
2
3.2
2
3.14
<
2
π
<
2
3.15
2
3.141
<
2
π
<
2
3.142
2
3.14159
<
2
π
<
2
3.14160
当指数是无理数时,该如何理解这个指数幂的值呢?
1. 尝试探究: ,其中π等于3.141592653……是一个无理数
2
π
探究任务三
尝试与发现
从而,这两个序列:
随着小数位的增加,两个有理数序列的值越来越接近π,他们为指数2为底数的指数值也越来越接近一个实数,这个实数就是
2
π
2
π
2
3.1
2
3.14
2
3.141
2
3.1415
2
3.14159
2
3.141592
2
3.2
2
3.15
2
3.142
2
3.1416
2
3.14160
2
3.141593
两边逼近的思想方法
概念形成
说明:
(1)无理数可以作为指数,无理指数幂是一个确定的实数。
(2)一般情况下,有理指数幂的运算法则同样适用于无理指数幂。
(3)无理指数幂的近似值可以用逼近的方式得到。
(4)一般不讨论a<0时的无理指数幂,因为会出现无法逼近的现象。
三、无理指数幂
定义:一般的当a>0,且t为无理数时, 都是一个确定的实数。
a
t
概念形成
四、实数指数幂
(1)当a>0,且指数t为任意实数时, 都是一个确定的实数,及时数指数幂 都有意义。
(2)实数指数幂包括整数指数幂、分数指数幂和无理数指数幂,且运算法则仍然成立。
a
t
a
t
整数指数幂 分数指数幂 无理数指数幂 实数指数幂
典例解析
例2:计算下列各式的值
(1)
(2)
例3:化简下列各式
(1)
(2)
典例解析
8
尝试与发现
课堂小结:
1.本节课了解整数指数幂 分数指数幂 无理数指数幂 实数指数幂的拓展,感受到了数学的发展和应用价值。
2.重点:根式的性质,根式与分数指数幂的转化,分数指数幂的概念和运算分数指数幂的理解。
难点:根式的性质和指数运算法则的求值化简。
3.提升了我们的类比归纳,数学抽象和逻辑推理的学科素养。
8
尝试与发现
课后作业:
1.小组合作探讨作业:课本例1 温馨提示,反例法
2.课后习题A组,B组1和2。
谢谢大家
2
Loading
4.1.1 实数指数幂及其运算
人教版高中数学B版必修第二册
励志公式:
①:
1.01
1.01
1.01
……
=
1.01
365
≈
37.78
>
1
②:
0.99
0.99
0.99
……
=
0.99
365
≈
0.03
<
1
数学告诉我们,积跬步以至千里,积怠惰以至深渊
情景引入
情景引入
实例:今年6月13日,三星堆遗址祭祀区考古发掘阶段性成果发布。北大考古年代学实验室的吴小红和她的团队通过碳十四年代测定,把三星堆“祭祀坑”的年代精确到了大约公元前1131年到1012年,使整个三星堆遗址乃至三星堆文化的研究走出了重要一步。
C-14在物体中每过约5730年会衰减一半
碳14计年的计算公式
( )
1
2
t
5730
复习回顾
一、整数指数幂
1
(-8)
0
=
;
10
3
1
2
-3
X
-3
=
8X
3
1
Y
-4
X
-6
=
Y
4
1
X
6
1
=
Y
6
X
4
10
-3
=
;
(2X)
-3
=
;
(
Y
2
X
3
-2
)
=
.
(1)
(2)
9的平方根为
=
=
±3
3
-2
0
与探究任务一
类比二次方根与三次方根,能否给出四次方根和五次方根的定义?
(1)若x =a,则称x为a的四次方根
4
I)当a=0时,a的四次方方根只有一个0,记作 0=0;
II)当a>0时,a有两个四次方根,他们互为相反数,正的四次方根为 a,负的四次方根为- a;
II)当a<0时,在实数范围内没有四次方根。
4
4
4
(2)若x =a,则称x为a的五次方根
5
在实数范围内,任意实数a有且只有一个五次方根,记为 a
5
探究新知
概念形成
二、分数指数幂:
0
1.a的n次方根
一般地,给定大于1的正整数n和实数a,如果存在实数x,使得x =a,则x称为a的n次方根。
n
①: 0=
②:n为偶数:当a>0时:a有两个n次方根为± a ,其中 a 为n次算术根;当a<0时: a 在实数范围内无意义。
n为奇数:a有唯一n次方根 a
2.性质
n
n
n
n
概念形成
2. 根式:
(1)定义:当 有意义的时候, 称为根式,读作“n次根号a”
n
a
n
a
根指数
被开方数
n
a
n
a
何时 有意义时? 的意义是什么呢?
概念深化
(2)根式的性质:
I):
II):当n为奇数时, ;当n为偶数时:
n
( )
a
n
=a
n
a
n
=a
n
n
a
=|a|
性质应用
例1 化简下列各式
(1)
(4)
(2)
(3)
(6)
(5)
尝试与发现
探究任务二
第一组任务:
1.当a>0时,计算 是多少?
5
a
10
2.观察计算结果的指数与a的指数10和根指数5有什么等量关系?
3.能否将 写成分数为指数的幂的形式?
5
10
第二组任务:
1.当a>0时,计算 是多少?
4
a
12
2.观察计算结果的指数与a的指数12和根指数4是否有等量关系?
3.能否将 写成分数为指数的幂的形式?
4
a
12
尝试与发现
5
a
10
=
5
(a)
2
5
=
a
2
=
a
5
10
(a>0)
进一步观察:
4
a
12
=
4
(a )
3
4
=
a
3
=
a
4
12
(a>0)
( )
( )
概念形成
3.分数指数幂
(1)为了方便,我们约定a>0,规定 (n∈N )
a
n
1
=
a
n
*
5
4
3
=
=
(5 )
3
4
1
=
5
4
3
3
(2)对于 m,n∈N 且 为既约分数,规定:
*
m
n
a
n
m
=
a
n
m
=
a
n
m
例如:
a
n
m
-
=
a
n
m
1
1
=
a
n
m
注意m,n的位置
( )
5
4
概念深化
发现
说明:①:只要根式 有意义, ,不一定非得a>0.
a
n
a
n
a
n
1
=
比如:
-8
3
=
(-8)
3
1
②:
(-8)
6
2
=
-8
6
2
但是, 没有意义,
-8
( )
6
2
这样,我们就将整数指数幂推广到了分数指数幂,即有理数指数幂。
(-8)
6
1
2
( )
=
( )
一般地,没有特殊说明,认为分数中指数幂中指数都是既约分数
概念深化
4.有理数指数幂运算法则:
( )
当s与t都是有理数时,有运算法则:
s
a
a
t
=
a
S+t
s
a
t
=
a
St
( )
ab
s
=
a
S
b
S
练一练:
自主阅读课本P6部分并作答
7
练一练
练一练
( )
8
3
1
2
=
2
2
=
4
( )
a
3
2
3
( )
b
4
1
3
=
a
2
3
3
2
1
3
3
1
3
6
1
=
3
2
=
9
①
②
③
探究新知
我们写不出 的精确的小数形式,但是3.1<π<3.2
2
π
得:
2
3.1
<
2
π
<
2
3.2
2
3.14
<
2
π
<
2
3.15
2
3.141
<
2
π
<
2
3.142
2
3.14159
<
2
π
<
2
3.14160
当指数是无理数时,该如何理解这个指数幂的值呢?
1. 尝试探究: ,其中π等于3.141592653……是一个无理数
2
π
探究任务三
尝试与发现
从而,这两个序列:
随着小数位的增加,两个有理数序列的值越来越接近π,他们为指数2为底数的指数值也越来越接近一个实数,这个实数就是
2
π
2
π
2
3.1
2
3.14
2
3.141
2
3.1415
2
3.14159
2
3.141592
2
3.2
2
3.15
2
3.142
2
3.1416
2
3.14160
2
3.141593
两边逼近的思想方法
概念形成
说明:
(1)无理数可以作为指数,无理指数幂是一个确定的实数。
(2)一般情况下,有理指数幂的运算法则同样适用于无理指数幂。
(3)无理指数幂的近似值可以用逼近的方式得到。
(4)一般不讨论a<0时的无理指数幂,因为会出现无法逼近的现象。
三、无理指数幂
定义:一般的当a>0,且t为无理数时, 都是一个确定的实数。
a
t
概念形成
四、实数指数幂
(1)当a>0,且指数t为任意实数时, 都是一个确定的实数,及时数指数幂 都有意义。
(2)实数指数幂包括整数指数幂、分数指数幂和无理数指数幂,且运算法则仍然成立。
a
t
a
t
整数指数幂 分数指数幂 无理数指数幂 实数指数幂
典例解析
例2:计算下列各式的值
(1)
(2)
例3:化简下列各式
(1)
(2)
典例解析
8
尝试与发现
课堂小结:
1.本节课了解整数指数幂 分数指数幂 无理数指数幂 实数指数幂的拓展,感受到了数学的发展和应用价值。
2.重点:根式的性质,根式与分数指数幂的转化,分数指数幂的概念和运算分数指数幂的理解。
难点:根式的性质和指数运算法则的求值化简。
3.提升了我们的类比归纳,数学抽象和逻辑推理的学科素养。
8
尝试与发现
课后作业:
1.小组合作探讨作业:课本例1 温馨提示,反例法
2.课后习题A组,B组1和2。
谢谢大家
