人教A版(2019)高中数学必修第二册 《正弦定理》名师课件(共43张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 《正弦定理》名师课件(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-24 19:21:02 | ||
图片预览









文档简介
(共43张PPT)
望天门山
李 白
天门中断楚江开
碧水东流至此回
两岸青山相对出
孤帆一片日边来
引课:古诗欣赏
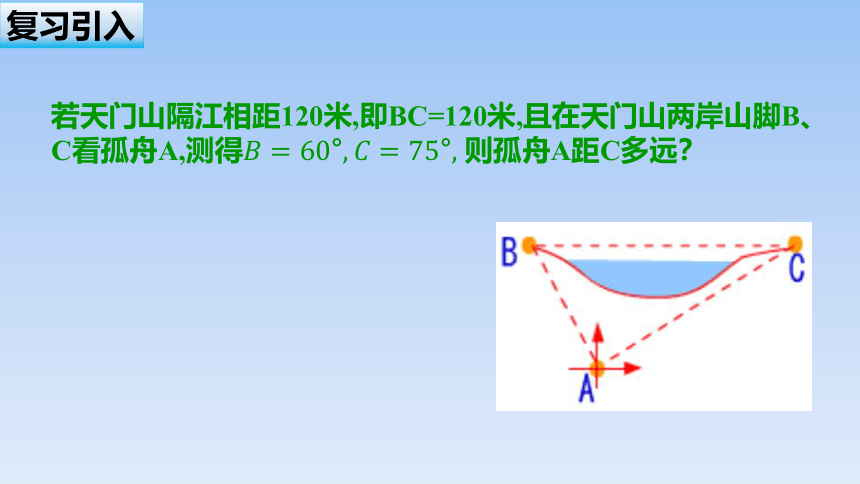
复习引入
若天门山隔江相距120米,即BC=120米,且在天门山两岸山脚B、C看孤舟A,测得 则孤舟A距C多远?
复习引入
人教A版同步教材名师课件
正弦定理
学习目标
学 习 目 标 核心素养
掌握正弦定理并能应用它解三角形 数学抽象
会判断三角形的形状 逻辑推理
能根据正弦定理确定三角形的解的个数 数学运算
A
B
C
在直角三角形中:
□
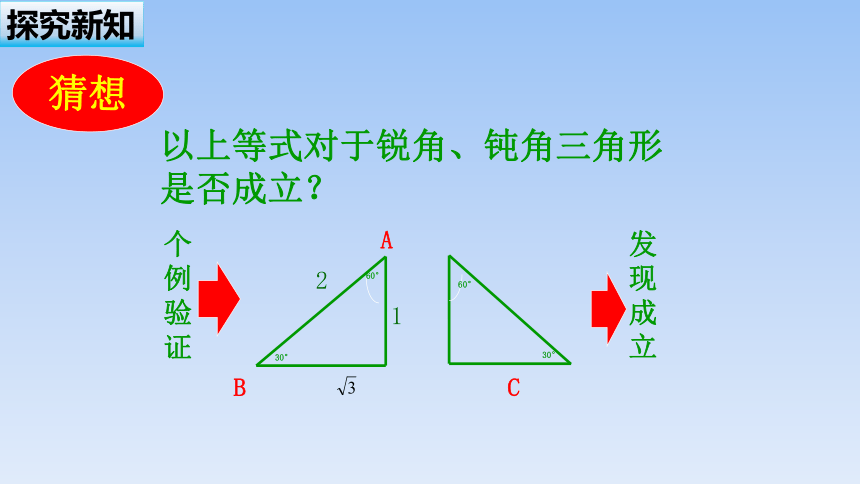
探究新知
猜想
以上等式对于锐角、钝角三角形是否成立?
个例验证
30°
60°
60°
30°
发现成立
2
1
A
B
C
探究新知
A
B
C
锐角三角形ABC
C
A
B
钝角三角形ABC
探究新知
向量的数量积运算中出现了角的余弦,而我们需要的是角的正弦.如何实现转化?
思考
探究新知
由诱导公式可知,我们可以通过构造角之间的互余关系,把边与角的余弦关系转化为正弦关系.
探究新知
如图,在锐角△ABC中,过点A作与垂直的单位向量,则与的夹角为 与的夹角为.
即
也即,
所以,.
同理,过点C作与垂直的单位向量,可得
因此
因为+ ,所以.
由分配律,得
探究新知
当△ABC是钝角三角形时,不妨设A为钝角过点A作与垂直的单位向量,则则与的夹角为 与的夹角为.仿照上述方法,同样可得
在一个三角形中,各边和它所对角的正弦的比相等,即
探究新知
正弦定理
思考1:利用正弦定理解三角形,至少已知几个元素?
思考2:正弦定理可以解决哪类解三角问题?
1.已知三角形的任意两个角与一边;
2.已知三角形的任意两边与其中一边的对角;
探究新知
在△ABC中,由正弦定理得则,由此可得正弦定理的下列变形:
正弦定理的常见变形
探究新知
在△ABC中,由正弦定理得则,由此可得正弦定理的下列变形:
正弦定理的常见变形
(是△ABC外接圆半径)
典例讲解
例1、设△ABC的内角A,B,C所对的边分别为a,b,c,且求角B的大小.
解析
由及正弦定理,得
.
方法归纳
当条件式中有边也有角时,往往要借助正弦定理化角为边或化边为角,统一后便于变形整理.
变式训练
解析
1.在△ABC中,角所对的边分别为,b,c,且满足
(1)求角的大小;
(2)求的最大值,并求取得最大值时角的大小.
(1)由正弦定理及已知条件,得
变式训练
解析
1.在△ABC中,角所对的边分别为,b,c,且满足
(1)求角的大小;
(2)求的最大值,并求取得最大值时角的大小.
综上所述,的最大值为
典例讲解
例2、在△ABC中,已知,则△ABC的形状是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形或直角三角形
解析
由正弦定理,得
,
故△ABC为等腰三角形或直角三角形.
D
方法归纳
通过边角转化判断三角形形状的方法
①化边为角.利用正弦定理化边为角,再根据角函数的有关知识得到三个内角的关系,进而确定角形的形状;
②化角为边.利用正弦定理化角为边,再根据代数恒等变换得到边的关系(如),进而确定三角形的形状.
③在△ABC中,;
④注意“等腰直角三角形”与“等腰三角形或直角三角形”的区别.
变式训练
解析
2.已知分别是△ABC的内角所对的边,满足则△ABC的形状是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.等腰直角三角形
解法一:由正弦定理及已知条件,得
C
变式训练
解析
2.已知分别是△ABC的内角所对的边,满足则△ABC的形状是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.等腰直角三角形
C
解法二:(R为△ABC外接圆的半径), ,
即△ABC为等边三角形.
典例讲解
例3、在△ABC中,求证:
证明
外接圆的半径),
同理,,
=右边.
所以原等式成立.
方法归纳
若恒等式的一边较复杂,一边较简单,则由复杂的一边入手,证明它等于另一边;若两边都比较复杂,往往使用归一法证明.三角恒等式的证明实质上就是消除等式左右两边的差异.
变式训练
证明
3.在△ABC中,求证:
等式成立.
典例讲解
例4、在△ABC中,,则________.
解析
设角的对边分别为,
,
则.
方法归纳
正、余弦定理的本质是任意三角形的边与角满足的方程,它能实现边角关系的转化:
(1)角的正弦齐次方程与边的齐次方程可互相转化;
(2)角的余弦可转化为边的二次齐次分式
变式训练
解析
4.设△ABC的内角所对的边分别为若三边的长为连续的三个正整数,且, 为( )
A.4 3 2 B.5 6 7 C. D.6 5 4
因为三边长为连续的三个正整数,且,所以
.
,
.
又由正弦定理可得,
D
典例讲解
例5、在△ABC中,角所对的边分别为
求证:
证明
(1)左边.
典例讲解
例5、在△ABC中,角所对的边分别为
求证:
证明
,
.
方法归纳
在三角形中的证明问题,若待证式中有边也有角,则证明时一般先借助正、余弦定理化角为边或化边为角,再通过代数变形或三角恒等变换使问题得到证明.
变式训练
证明
5.在△ABC中,
,
,
.
.
记R为△ABC外接圆的半径,
.
变式训练
解析
6.△ABC的内角所对的边分别为
(1)若满足;
(2)若满足.
,
.
典例讲解
例6、在△ABC中,角所对的边分别为,且满足(-)
(1)求角;
(2)若,求的取值范围.
解析
.
.
典例讲解
例6、在△ABC中,角所对的边分别为,且满足(-)
(1)求角;
(2)若,求的取值范围.
解析
.
,
方法归纳
求三角形中有关最值与范围问题的方法
(1)解三角形中有关最值问题的关键:利用正弦定理或余弦定理、三角恒等变换将有关问题转化为关于某一个角的三角函数,或某一边的函数,进而求出其最值.
(2)对于求角的范围这种类型的问题,在解答时,先求出该角的某一三角函数值的取值范围,再根据该函数的单调性求出其取值范围.
变式训练
解析
7.在△ABC中,,则角A的取值范围是__________.
由正弦定理,
典例讲解
例7、如图,在,点D在BC边上,且
(1)求;(2)求BD,AC的长.
(1)因为.
(2)在△ABD中,由正弦定理得
在△ABC中,根据余弦定理,得.
解析
方法归纳
在几何图形中求解问题时,应注意寻找相应的三角形,并在三角形中运用正、余弦定理,特别是涉及公共边时,要利用公共边来进行过渡.
当题目中出现多个三角形时,要弄清楚各三角形中的边角关系,分析已知和未知的关系,合理选择正弦定理与余弦定理来求解.
变式训练
解析
8.如图,在平面四边形ABCD中,AD=1,CD.
(1)求cos∠CAD的值;
(2)若的长.
(1)在△ADC中,由余弦定理的推论,得
变式训练
解析
8.如图,在平面四边形ABCD中,AD=1,CD.
(1)求cos∠CAD的值;
(2)若的长.
(2)因为∠ 为四边形ABCD的内角,
,.
.
.
当堂练习
1.在△ABC中,角的对边为,若,,则A=( )
A.45° B.45°或135 C.135° D.60°或120
2.在△ABC中,则角C的取值范围是( )
3.△ABC中,最大边与最小边之比为,则最大角为( )
A.45° B.60° C.75° D.90°
A
A
归纳小结
正弦定理
已知两边和其中一边的对角,求其他的边和角
形式
边角互化—判断三角形的形状
(为△ABC外接圆的半径)
应用—解三角形
已知两角和一边,求其他的边和角
作 业
课本48页 练习:1、2、3
望天门山
李 白
天门中断楚江开
碧水东流至此回
两岸青山相对出
孤帆一片日边来
引课:古诗欣赏
复习引入
若天门山隔江相距120米,即BC=120米,且在天门山两岸山脚B、C看孤舟A,测得 则孤舟A距C多远?
复习引入
人教A版同步教材名师课件
正弦定理
学习目标
学 习 目 标 核心素养
掌握正弦定理并能应用它解三角形 数学抽象
会判断三角形的形状 逻辑推理
能根据正弦定理确定三角形的解的个数 数学运算
A
B
C
在直角三角形中:
□
探究新知
猜想
以上等式对于锐角、钝角三角形是否成立?
个例验证
30°
60°
60°
30°
发现成立
2
1
A
B
C
探究新知
A
B
C
锐角三角形ABC
C
A
B
钝角三角形ABC
探究新知
向量的数量积运算中出现了角的余弦,而我们需要的是角的正弦.如何实现转化?
思考
探究新知
由诱导公式可知,我们可以通过构造角之间的互余关系,把边与角的余弦关系转化为正弦关系.
探究新知
如图,在锐角△ABC中,过点A作与垂直的单位向量,则与的夹角为 与的夹角为.
即
也即,
所以,.
同理,过点C作与垂直的单位向量,可得
因此
因为+ ,所以.
由分配律,得
探究新知
当△ABC是钝角三角形时,不妨设A为钝角过点A作与垂直的单位向量,则则与的夹角为 与的夹角为.仿照上述方法,同样可得
在一个三角形中,各边和它所对角的正弦的比相等,即
探究新知
正弦定理
思考1:利用正弦定理解三角形,至少已知几个元素?
思考2:正弦定理可以解决哪类解三角问题?
1.已知三角形的任意两个角与一边;
2.已知三角形的任意两边与其中一边的对角;
探究新知
在△ABC中,由正弦定理得则,由此可得正弦定理的下列变形:
正弦定理的常见变形
探究新知
在△ABC中,由正弦定理得则,由此可得正弦定理的下列变形:
正弦定理的常见变形
(是△ABC外接圆半径)
典例讲解
例1、设△ABC的内角A,B,C所对的边分别为a,b,c,且求角B的大小.
解析
由及正弦定理,得
.
方法归纳
当条件式中有边也有角时,往往要借助正弦定理化角为边或化边为角,统一后便于变形整理.
变式训练
解析
1.在△ABC中,角所对的边分别为,b,c,且满足
(1)求角的大小;
(2)求的最大值,并求取得最大值时角的大小.
(1)由正弦定理及已知条件,得
变式训练
解析
1.在△ABC中,角所对的边分别为,b,c,且满足
(1)求角的大小;
(2)求的最大值,并求取得最大值时角的大小.
综上所述,的最大值为
典例讲解
例2、在△ABC中,已知,则△ABC的形状是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形或直角三角形
解析
由正弦定理,得
,
故△ABC为等腰三角形或直角三角形.
D
方法归纳
通过边角转化判断三角形形状的方法
①化边为角.利用正弦定理化边为角,再根据角函数的有关知识得到三个内角的关系,进而确定角形的形状;
②化角为边.利用正弦定理化角为边,再根据代数恒等变换得到边的关系(如),进而确定三角形的形状.
③在△ABC中,;
④注意“等腰直角三角形”与“等腰三角形或直角三角形”的区别.
变式训练
解析
2.已知分别是△ABC的内角所对的边,满足则△ABC的形状是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.等腰直角三角形
解法一:由正弦定理及已知条件,得
C
变式训练
解析
2.已知分别是△ABC的内角所对的边,满足则△ABC的形状是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.等腰直角三角形
C
解法二:(R为△ABC外接圆的半径), ,
即△ABC为等边三角形.
典例讲解
例3、在△ABC中,求证:
证明
外接圆的半径),
同理,,
=右边.
所以原等式成立.
方法归纳
若恒等式的一边较复杂,一边较简单,则由复杂的一边入手,证明它等于另一边;若两边都比较复杂,往往使用归一法证明.三角恒等式的证明实质上就是消除等式左右两边的差异.
变式训练
证明
3.在△ABC中,求证:
等式成立.
典例讲解
例4、在△ABC中,,则________.
解析
设角的对边分别为,
,
则.
方法归纳
正、余弦定理的本质是任意三角形的边与角满足的方程,它能实现边角关系的转化:
(1)角的正弦齐次方程与边的齐次方程可互相转化;
(2)角的余弦可转化为边的二次齐次分式
变式训练
解析
4.设△ABC的内角所对的边分别为若三边的长为连续的三个正整数,且, 为( )
A.4 3 2 B.5 6 7 C. D.6 5 4
因为三边长为连续的三个正整数,且,所以
.
,
.
又由正弦定理可得,
D
典例讲解
例5、在△ABC中,角所对的边分别为
求证:
证明
(1)左边.
典例讲解
例5、在△ABC中,角所对的边分别为
求证:
证明
,
.
方法归纳
在三角形中的证明问题,若待证式中有边也有角,则证明时一般先借助正、余弦定理化角为边或化边为角,再通过代数变形或三角恒等变换使问题得到证明.
变式训练
证明
5.在△ABC中,
,
,
.
.
记R为△ABC外接圆的半径,
.
变式训练
解析
6.△ABC的内角所对的边分别为
(1)若满足;
(2)若满足.
,
.
典例讲解
例6、在△ABC中,角所对的边分别为,且满足(-)
(1)求角;
(2)若,求的取值范围.
解析
.
.
典例讲解
例6、在△ABC中,角所对的边分别为,且满足(-)
(1)求角;
(2)若,求的取值范围.
解析
.
,
方法归纳
求三角形中有关最值与范围问题的方法
(1)解三角形中有关最值问题的关键:利用正弦定理或余弦定理、三角恒等变换将有关问题转化为关于某一个角的三角函数,或某一边的函数,进而求出其最值.
(2)对于求角的范围这种类型的问题,在解答时,先求出该角的某一三角函数值的取值范围,再根据该函数的单调性求出其取值范围.
变式训练
解析
7.在△ABC中,,则角A的取值范围是__________.
由正弦定理,
典例讲解
例7、如图,在,点D在BC边上,且
(1)求;(2)求BD,AC的长.
(1)因为.
(2)在△ABD中,由正弦定理得
在△ABC中,根据余弦定理,得.
解析
方法归纳
在几何图形中求解问题时,应注意寻找相应的三角形,并在三角形中运用正、余弦定理,特别是涉及公共边时,要利用公共边来进行过渡.
当题目中出现多个三角形时,要弄清楚各三角形中的边角关系,分析已知和未知的关系,合理选择正弦定理与余弦定理来求解.
变式训练
解析
8.如图,在平面四边形ABCD中,AD=1,CD.
(1)求cos∠CAD的值;
(2)若的长.
(1)在△ADC中,由余弦定理的推论,得
变式训练
解析
8.如图,在平面四边形ABCD中,AD=1,CD.
(1)求cos∠CAD的值;
(2)若的长.
(2)因为∠ 为四边形ABCD的内角,
,.
.
.
当堂练习
1.在△ABC中,角的对边为,若,,则A=( )
A.45° B.45°或135 C.135° D.60°或120
2.在△ABC中,则角C的取值范围是( )
3.△ABC中,最大边与最小边之比为,则最大角为( )
A.45° B.60° C.75° D.90°
A
A
归纳小结
正弦定理
已知两边和其中一边的对角,求其他的边和角
形式
边角互化—判断三角形的形状
(为△ABC外接圆的半径)
应用—解三角形
已知两角和一边,求其他的边和角
作 业
课本48页 练习:1、2、3
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
