人教A版(2019)高中数学必修第二册 《余弦定理、正弦定理应用举例》名师课件(共30张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 《余弦定理、正弦定理应用举例》名师课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-24 19:22:21 | ||
图片预览










文档简介
(共30张PPT)
人教A版同步教材名师课件
余弦定理、正弦定理应用举例
学习目标
学 习 目 标 核心素养
掌握利用正、余弦定理解决测量问题. 数学运算
体会利用正、余弦定理和三角形面积公式解决与三角形有关的几何问题 数学运算
了解正、余弦定理在生活中的应用 数学建模
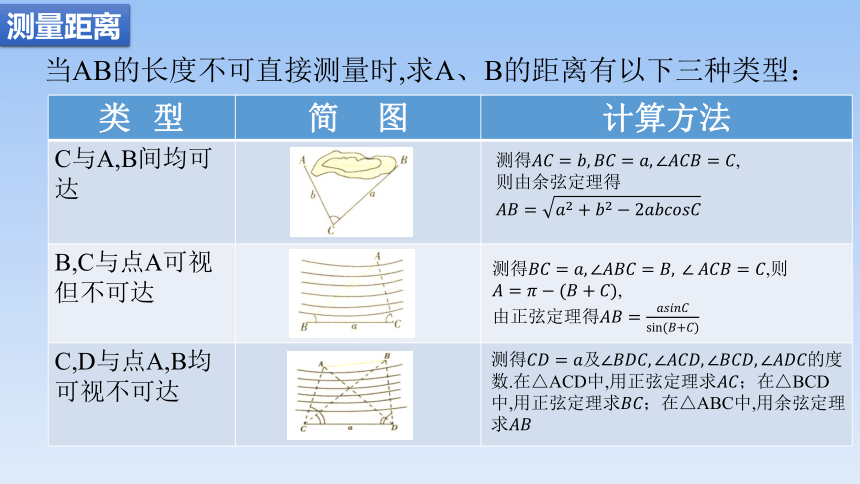
当AB的长度不可直接测量时,求A、B的距离有以下三种类型:
测量距离
类 型 简 图 计算方法
C与A,B间均可达
B,C与点A可视但不可达
C,D与点A,B均可视不可达
测得,
则由余弦定理得
测得,则,
由正弦定理得
测得及的度数.在△ACD中,用正弦定理求;在△BCD中,用正弦定理求;在△ABC中,用余弦定理求
测量距离问题的解题思路
选择合适的辅助测量点,构造三角形,将问题转化为求某个三角形的边长问题,从而利用正、余弦定理求解构建数学模型时,尽量把已知元素放在同一个三角形中.
测量距离
①测量从一个可到达的点到一个不可到达的点之间的距离问题,一般可转化为已知两个角和条边解三角形的问题,从而运用正弦定理去解决.
②测量两个不可到达的点之间的距离问题,一般先把求距离问题转化为运用余弦定理求三角形的边长的问题,然后把求未知的边长问题转化为只有一点不能到达的两点之间距离的测量问题,最后运用正弦定理解决.
测量距离
典例讲解
例1、在“联合行动-2019E”演习中,红方为了准确分析战场形势,在两个相距的军事基地C处和D处测得蓝方两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°, ∠DCA=60°, ∠ACB=45°,如图所示,求蓝方这两支精锐部队的距离.
解法一:,
.
在△BCD中,,
由正弦定理,得.
,
,∴蓝方这两支精锐部队的距离为
解析
典例讲解
例1、在“联合行动-2019E”演习中,红方为了准确分析战场形势,在两个相距的军事基地C处和D处测得蓝方两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°, ∠DCA=60°, ∠ACB=45°,如图所示,求蓝方这两支精锐部队的距离.
解析
解法二:,
在△BCD中,
△ABC中,
,
,∴蓝方这两支精锐部队的距离为
方法归纳
解决距离问题一般要注意:
①选定或构造的三角形要确定,即确定在哪一个三角形中求解;
②当角边对应,且角的条件较多时,一般用正弦定理,当角的条件较少,且角边不对应时,用余弦定理较多.
变式训练
解析
1、某游轮在A处看灯塔B在A的北偏东方向,距离为海里,灯塔C在A的北偏西方向,距离为海里,游轮由A处向正北方向航行到D处时再看灯塔B,B在南偏东方向上,则C与D的距离为( )
A.20海里 B. 海里 C. 海里 D. 24海里
B
在△ABD中,因为灯塔B在A的北偏东方向上,距离为海里,游轮由A处向正北方向航行到D处时,再看灯塔B,B在南偏东方向上,所以由正弦定理
,
,
测量高度
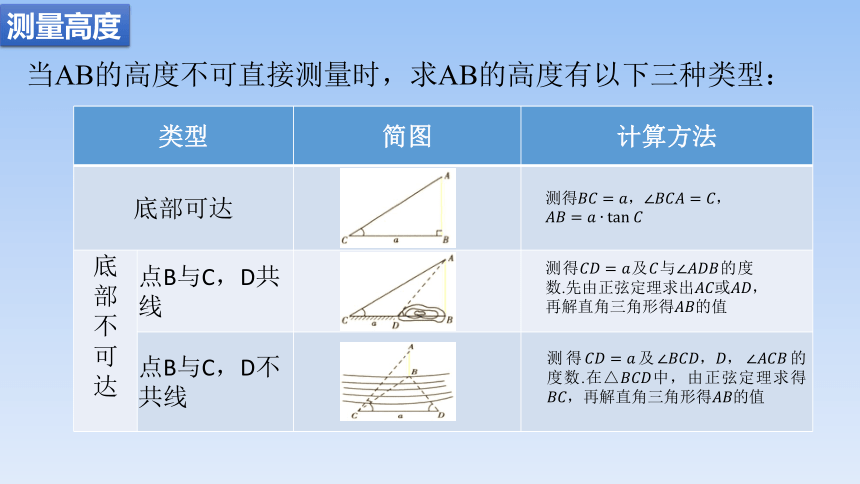
当AB的高度不可直接测量时,求AB的高度有以下三种类型:
类型 简图 计算方法
底部可达
底 部 不 可 达 点B与C,D共线
点B与C,D不共线
测得
测得及与的度数.先由正弦定理求出或,再解直角三角形得的值
测得及的度数.在△中,由正弦定理求得,再解直角三角形得的值
测量高度问题的解题思路
高度的测量主要是一些底部不能到达或者无法直接测量的物体的高度.常用正弦定理或余弦定理计算出物体的顶部或底部到一个可到达的点之间的距离,然后转化为解直角三角形的问题.这类物体高度的测量是在与地面垂直的竖直平面内构造三角形,再依据条件利用正、余弦定理解其中的一个或者同角三角形,从而求出待测物体的高度.
测量高度
典例讲解
例2、某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度,如图,在C处进行该仪器的弹射,观测点A,B两地相距在A地听到弹射声音的时间比B地晚s. A地测得该仪器在C处时的俯角为A地测得该仪器在最高点H时的仰角为求该仪器的垂直弹射高度CH.(声音在空气中的传播速度为340m/s)
在△ABC中,根据余弦定理得,解得x=420.
.
,
故该仪器的垂直弹射高度.
解析
变式训练
解析
2.如图,河边有一座塔OP,其高为20m,河对面岸上有A,B两点与塔底在同一水平面上,由塔顶部测得A,B两点的俯角分别为和而且A,B两点分别与塔底部O连线成角,则A,B两点的距离为( )
A.20m
由已知得.
在△AOB中,由余弦定理得
,
C
测量角度
(1)测量角度问题的情境属于“根据需要,对某些物体定位”.测量数据越精确,定位精度越高.
(2)测量角度问题主要是指在海上或空中测量角度,如确定目标的方位,观察某一建筑物的视角等.解决问题的关键是根据题意和图形及有关概念,从实际问题中抽象出一个或几个三角形,确定所求的角在哪个三角形中,该三角形中已知哪些量,需要求哪些量.然后通过解这些三角形得到所要求的量,从而得到实际问题的解.解题时应认真审题,结合图形去选择方法.
解决测量角度问题的注意点:
①明确方位角和方向角的含义;
②分析题意,分清已知与所求,并根据题意画出正确的示意图;
③将实际问题转化为可用数学方法解决的问题后,注意正、余弦定理的使用.
测量角度
典例讲解
例3、“一带一路”国际合作高峰论坛在北京举行,会议期间达成了多项国际合作协议,其中有一项是在某国投资建设一个深水港码头,如图,工程师为了了解深水港码头海域海底的构造,在海平面内一条直线上的A,B,C三点进行测量.已知AB=60m, BC=120m,于A处测得水深AD=120m,于B处测得水深BE=200m,于C处测得水深CF=150m,则cos∠DEF=______.
由题中所给数据得,
,
.
在△DEF中,由余弦定理的推论,得
.
解析
如图所示,作DM∥AC交BE于N,交CF于M,作FH∥AC交BE于H.
方法归纳
解三角形应用题的一般步骤
变式训练
解析
3.如图,位于A处的信息中心获悉:在其正东方向40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西相距20海里的C处的乙船,现乙船朝北偏东的方向即沿直线CB前往B处救援,求
在△ABC中,AB=40,AC=20, =
由余弦定理,,
.
,
.
在△ABC中,已知三边及三内角,如何计算△ABC的面积?
作BC边的高线AD,
在Rt△ABD中:;在Rt△ACD中:.
从而.
A
B
C
D
c
b
三角形面积公式应用
∴
三角形的面积公式
典例讲解
例4、如图所示,已知半圆O的直径为2,点A为直径延长线上的一点,OA=2,点B为半圆上任意一点,以AB为一边作等边三角形ABC,求B在什么位置时,四边形OACB的面积最大.
由余弦定理得,
,
时,四边形OACB的面积最大.
解析
方法归纳
(1)处理三角形中的最值问题时,常见的类型是转化为三角函数求最值;
(2)三角形中面积的最大值或最小值问题可以运用正弦定理或余弦定理建立所求变量与三角形的角或边之间的函数关系,利用正、余弦函数的有界性或二次函数的知识解决问题.
在三角形中选择面积公式时可根据角或边选择如已知角A,一般用或,一般用.
变式训练
解析
4.已知为△ABC的三边,且c=2,b=,则△ABC的面积的最大值为_______.
由余弦定理的推论,.
,所以△ABC的面积,
当且仅当取得最大值,故△ABC的面积的最大值为.
典例讲解
例5、在△中,角的对边分别为满足.
(1)求的大小;
(2)若△ 外接圆的半径为,△ 的面积为求△ 的周长.
解析
(1)由余弦定理及,
,
又由正弦定理,可得
.
典例讲解
例5、在△中,角的对边分别为满足.
(1)求的大小;
(2)若△ 外接圆的半径为,△ 的面积为求△ 的周长.
解析
(2)由(1)可知,又知△ABC外接圆的半径为,
则由正弦定理得.
根据余弦定理, ,
所以△的周长为.
方法归纳
在解三角形时,常用正弦定理或余弦定理“化边为角”或“化角为边”,从而发现三角形中各元素之间的关系.在实际应用中,也常建立数学模型将实际问题转化为数学问题来解决.因此要理解并领悟转化与化归的数学思想,以便应用到要解决的问题中去.
转化与化归思想
变式训练
解析
5.在△ABC中,分别是角的对边,
(1)求的值及△ABC的面积;
(2)若,求的大小.
.
当堂练习
1.学校体育馆的人字屋架为等腰三角形,如图,测得AC的长度为则其跨度AB的长为( )
A.12 B.8m
2.甲骑电动自行车以24km/h的速度沿着正北方向的公路行驶,在点A处望见电视塔S在电动车的北偏东方向上,15min后到点B处望见电视塔在电动车的北偏东方向上,则电动车在点B时与电视塔S的距离是( )
A.6 km D.3 km
D
C
当堂练习
3.某公司要测量一水塔CD的高度,测量人员在地面选择了A,B两个观测点,且A,B,C三点在同一直线上,如图所示,在A处测得该水塔顶端D的仰角为,在B处测得该水塔顶端D的仰角为.若则水塔CD的高度为( )
4.如图所示为起重机装置示意图.支杆BC=10m,吊杆AC=15m,吊索,起吊的货物与岸的距离AD为( )
A.30m D.45m
B
B
归纳小结
应用举例
几何计算问题
解三角形
测量问题
求解面积
测量距离
测量高度
测量角度
作 业
课本51页 练习:1、2、3
人教A版同步教材名师课件
余弦定理、正弦定理应用举例
学习目标
学 习 目 标 核心素养
掌握利用正、余弦定理解决测量问题. 数学运算
体会利用正、余弦定理和三角形面积公式解决与三角形有关的几何问题 数学运算
了解正、余弦定理在生活中的应用 数学建模
当AB的长度不可直接测量时,求A、B的距离有以下三种类型:
测量距离
类 型 简 图 计算方法
C与A,B间均可达
B,C与点A可视但不可达
C,D与点A,B均可视不可达
测得,
则由余弦定理得
测得,则,
由正弦定理得
测得及的度数.在△ACD中,用正弦定理求;在△BCD中,用正弦定理求;在△ABC中,用余弦定理求
测量距离问题的解题思路
选择合适的辅助测量点,构造三角形,将问题转化为求某个三角形的边长问题,从而利用正、余弦定理求解构建数学模型时,尽量把已知元素放在同一个三角形中.
测量距离
①测量从一个可到达的点到一个不可到达的点之间的距离问题,一般可转化为已知两个角和条边解三角形的问题,从而运用正弦定理去解决.
②测量两个不可到达的点之间的距离问题,一般先把求距离问题转化为运用余弦定理求三角形的边长的问题,然后把求未知的边长问题转化为只有一点不能到达的两点之间距离的测量问题,最后运用正弦定理解决.
测量距离
典例讲解
例1、在“联合行动-2019E”演习中,红方为了准确分析战场形势,在两个相距的军事基地C处和D处测得蓝方两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°, ∠DCA=60°, ∠ACB=45°,如图所示,求蓝方这两支精锐部队的距离.
解法一:,
.
在△BCD中,,
由正弦定理,得.
,
,∴蓝方这两支精锐部队的距离为
解析
典例讲解
例1、在“联合行动-2019E”演习中,红方为了准确分析战场形势,在两个相距的军事基地C处和D处测得蓝方两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°, ∠DCA=60°, ∠ACB=45°,如图所示,求蓝方这两支精锐部队的距离.
解析
解法二:,
在△BCD中,
△ABC中,
,
,∴蓝方这两支精锐部队的距离为
方法归纳
解决距离问题一般要注意:
①选定或构造的三角形要确定,即确定在哪一个三角形中求解;
②当角边对应,且角的条件较多时,一般用正弦定理,当角的条件较少,且角边不对应时,用余弦定理较多.
变式训练
解析
1、某游轮在A处看灯塔B在A的北偏东方向,距离为海里,灯塔C在A的北偏西方向,距离为海里,游轮由A处向正北方向航行到D处时再看灯塔B,B在南偏东方向上,则C与D的距离为( )
A.20海里 B. 海里 C. 海里 D. 24海里
B
在△ABD中,因为灯塔B在A的北偏东方向上,距离为海里,游轮由A处向正北方向航行到D处时,再看灯塔B,B在南偏东方向上,所以由正弦定理
,
,
测量高度
当AB的高度不可直接测量时,求AB的高度有以下三种类型:
类型 简图 计算方法
底部可达
底 部 不 可 达 点B与C,D共线
点B与C,D不共线
测得
测得及与的度数.先由正弦定理求出或,再解直角三角形得的值
测得及的度数.在△中,由正弦定理求得,再解直角三角形得的值
测量高度问题的解题思路
高度的测量主要是一些底部不能到达或者无法直接测量的物体的高度.常用正弦定理或余弦定理计算出物体的顶部或底部到一个可到达的点之间的距离,然后转化为解直角三角形的问题.这类物体高度的测量是在与地面垂直的竖直平面内构造三角形,再依据条件利用正、余弦定理解其中的一个或者同角三角形,从而求出待测物体的高度.
测量高度
典例讲解
例2、某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度,如图,在C处进行该仪器的弹射,观测点A,B两地相距在A地听到弹射声音的时间比B地晚s. A地测得该仪器在C处时的俯角为A地测得该仪器在最高点H时的仰角为求该仪器的垂直弹射高度CH.(声音在空气中的传播速度为340m/s)
在△ABC中,根据余弦定理得,解得x=420.
.
,
故该仪器的垂直弹射高度.
解析
变式训练
解析
2.如图,河边有一座塔OP,其高为20m,河对面岸上有A,B两点与塔底在同一水平面上,由塔顶部测得A,B两点的俯角分别为和而且A,B两点分别与塔底部O连线成角,则A,B两点的距离为( )
A.20m
由已知得.
在△AOB中,由余弦定理得
,
C
测量角度
(1)测量角度问题的情境属于“根据需要,对某些物体定位”.测量数据越精确,定位精度越高.
(2)测量角度问题主要是指在海上或空中测量角度,如确定目标的方位,观察某一建筑物的视角等.解决问题的关键是根据题意和图形及有关概念,从实际问题中抽象出一个或几个三角形,确定所求的角在哪个三角形中,该三角形中已知哪些量,需要求哪些量.然后通过解这些三角形得到所要求的量,从而得到实际问题的解.解题时应认真审题,结合图形去选择方法.
解决测量角度问题的注意点:
①明确方位角和方向角的含义;
②分析题意,分清已知与所求,并根据题意画出正确的示意图;
③将实际问题转化为可用数学方法解决的问题后,注意正、余弦定理的使用.
测量角度
典例讲解
例3、“一带一路”国际合作高峰论坛在北京举行,会议期间达成了多项国际合作协议,其中有一项是在某国投资建设一个深水港码头,如图,工程师为了了解深水港码头海域海底的构造,在海平面内一条直线上的A,B,C三点进行测量.已知AB=60m, BC=120m,于A处测得水深AD=120m,于B处测得水深BE=200m,于C处测得水深CF=150m,则cos∠DEF=______.
由题中所给数据得,
,
.
在△DEF中,由余弦定理的推论,得
.
解析
如图所示,作DM∥AC交BE于N,交CF于M,作FH∥AC交BE于H.
方法归纳
解三角形应用题的一般步骤
变式训练
解析
3.如图,位于A处的信息中心获悉:在其正东方向40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西相距20海里的C处的乙船,现乙船朝北偏东的方向即沿直线CB前往B处救援,求
在△ABC中,AB=40,AC=20, =
由余弦定理,,
.
,
.
在△ABC中,已知三边及三内角,如何计算△ABC的面积?
作BC边的高线AD,
在Rt△ABD中:;在Rt△ACD中:.
从而.
A
B
C
D
c
b
三角形面积公式应用
∴
三角形的面积公式
典例讲解
例4、如图所示,已知半圆O的直径为2,点A为直径延长线上的一点,OA=2,点B为半圆上任意一点,以AB为一边作等边三角形ABC,求B在什么位置时,四边形OACB的面积最大.
由余弦定理得,
,
时,四边形OACB的面积最大.
解析
方法归纳
(1)处理三角形中的最值问题时,常见的类型是转化为三角函数求最值;
(2)三角形中面积的最大值或最小值问题可以运用正弦定理或余弦定理建立所求变量与三角形的角或边之间的函数关系,利用正、余弦函数的有界性或二次函数的知识解决问题.
在三角形中选择面积公式时可根据角或边选择如已知角A,一般用或,一般用.
变式训练
解析
4.已知为△ABC的三边,且c=2,b=,则△ABC的面积的最大值为_______.
由余弦定理的推论,.
,所以△ABC的面积,
当且仅当取得最大值,故△ABC的面积的最大值为.
典例讲解
例5、在△中,角的对边分别为满足.
(1)求的大小;
(2)若△ 外接圆的半径为,△ 的面积为求△ 的周长.
解析
(1)由余弦定理及,
,
又由正弦定理,可得
.
典例讲解
例5、在△中,角的对边分别为满足.
(1)求的大小;
(2)若△ 外接圆的半径为,△ 的面积为求△ 的周长.
解析
(2)由(1)可知,又知△ABC外接圆的半径为,
则由正弦定理得.
根据余弦定理, ,
所以△的周长为.
方法归纳
在解三角形时,常用正弦定理或余弦定理“化边为角”或“化角为边”,从而发现三角形中各元素之间的关系.在实际应用中,也常建立数学模型将实际问题转化为数学问题来解决.因此要理解并领悟转化与化归的数学思想,以便应用到要解决的问题中去.
转化与化归思想
变式训练
解析
5.在△ABC中,分别是角的对边,
(1)求的值及△ABC的面积;
(2)若,求的大小.
.
当堂练习
1.学校体育馆的人字屋架为等腰三角形,如图,测得AC的长度为则其跨度AB的长为( )
A.12 B.8m
2.甲骑电动自行车以24km/h的速度沿着正北方向的公路行驶,在点A处望见电视塔S在电动车的北偏东方向上,15min后到点B处望见电视塔在电动车的北偏东方向上,则电动车在点B时与电视塔S的距离是( )
A.6 km D.3 km
D
C
当堂练习
3.某公司要测量一水塔CD的高度,测量人员在地面选择了A,B两个观测点,且A,B,C三点在同一直线上,如图所示,在A处测得该水塔顶端D的仰角为,在B处测得该水塔顶端D的仰角为.若则水塔CD的高度为( )
4.如图所示为起重机装置示意图.支杆BC=10m,吊杆AC=15m,吊索,起吊的货物与岸的距离AD为( )
A.30m D.45m
B
B
归纳小结
应用举例
几何计算问题
解三角形
测量问题
求解面积
测量距离
测量高度
测量角度
作 业
课本51页 练习:1、2、3
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
