沪科版七年级上册数学 1.3有理数的大小 课件(共19张PPT)
文档属性
| 名称 | 沪科版七年级上册数学 1.3有理数的大小 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 672.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-24 18:43:30 | ||
图片预览






文档简介
(共20张PPT)
1.3 有理数的大小
复习导入
进入了有理数的世界,我们已经学习了哪些知识?
一起来回顾一下吧!
1、任意写出两位正数,在数轴上画出表示它们的点,看看较大的数与较小的数的对应点的位置有何关系?
2、生活常识告诉我们,1℃与-2℃哪个温度高?-1℃与0℃哪个温度高?这个关系在温度计上表现为怎样的情况?
即较大的数表示的点在较小的数表示的点的右侧。
即温度高表示的液面在温度低的上面。
生活中的数学
若小文比小强矮8cm,记着:-8cm;小冬比小强矮10cm,记着:-10cm. 小文和小冬比较,结果小文高,所以-8>-10。
考试的时候,被老师扣2分比被老师扣5分的分数要高,所以-2>-5。
这就说明负数间也是可以比较大小的!
我们规定铅球的质量超过标准质量的部分记为正,低于标准质量的部分记为负.现有四个铅球的记录分别为-5克,+4克,+2克,-2克。哪个铅球最重,哪个最轻?
生活中的数学
合肥在某冬日6时,14时,16时,23时的气温分别为-5℃ ,4 ℃ ,2 ℃和-2 ℃.哪个时刻的气温最高,哪个时刻的气温最低?
上述问题都可以归结为比较有理数“ -5,4,+2,-2 ”的大小.
活动探究1
某地一天中5个不同的时刻的气温分别是
- 2℃, -5℃, 4℃, 0℃,2 ℃.
10
10
5
5
0
0
-5
-5
-10
-10
-5
-2
4
0
单位:℃
(1)请你按照由低到高的顺序把不同时刻的气温排列出来。
-5℃<-2℃<0℃< 2 ℃ < 4℃
2
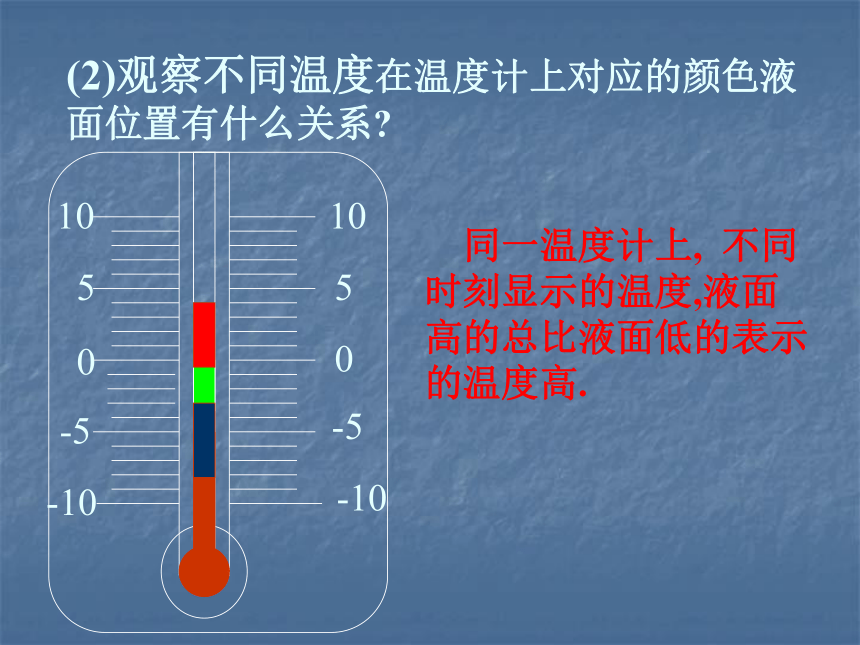
(2)观察不同温度在温度计上对应的颜色液面位置有什么关系
同一温度计上, 不同时刻显示的温度,液面高的总比液面低的表示的温度高.
10
10
5
5
0
0
-5
-5
-10
-10
把有理数 -3、-5、 4、 0、2表示在数轴上,这些数的大小与其在数轴上的点的位置有什么关系?
-5 -4 -3 -2 -1 0 1 2 3 4 5
-3
-5
4
0
活动探究2
2
-5℃<-3℃<0℃< 2 ℃ < 4℃
在数轴上表示的两个数,右边的数总比左边的数大。
正数都大于0,0大于负数,正数大于一切负数。
规律:
知识总结1
活动探究3
1、在数轴上表示下列各对数,并比较它们的大小;
⑴2和7; ⑵-6和-1;
⑶-2和-5; ⑷-2 和-1.5
2、求上述各对数的绝对值,并比较它们的大小。上面各对数的大小与他们的绝对值的大小有什么关系?
知识总结2
两个正数大小比较:
两个负数大小比较:
一正一负大小比较:
正数与零大小比较:
负数与零大小比较:
绝对值大的较大
绝对值大的反而小
正数大于负数
正数都大于零
负数都小于零
有理数大小比较法则:
1、在数轴上表示的两个数,右边的总比左边的数大。
2、正数都大于零,负数都小于零,正数大于负数。
3、两个正数比较大小,绝对值大的数较大;两个负
数比较大小,绝对值大的数反而小。
知识整理
例 比较下列每对数的大小,并说明理由:
(1)1与-10; (2)-0.001与0 (3)
解:
(1) 1>-10
(2)-0.001<0
(3)因为
(两个负数比较大小,绝对值大的数反而小)
所以
(正数大于一切负数)
(负数都小于零)
且
小试牛刀
1、(抢答)用“>”或“<”号填空:
(1)-6____-4
(3) 0_____-9
(4)
( 5 )
( 2 )
(6)-0.01___ 0.001
2、把下面各组数表示在数轴上,并按从小到大的顺序用“ < ”好号连接:
⑴-7,-3,-1; ⑵ 5,0,-4 ,-2,
3、比较下面各对数的大小,并说明理由:
⑴ 与 ; ⑵-3 与 +1;
⑶ -1 与 0; ⑷ - 与 -
4、利用数轴求出大于- 3.2并且小于3.2的整数。
小试牛刀
(1)有没有最小的正数?有没有最大的负数?
(2)有没有绝对值最小的有理数?若有,请把它写出来.
想一想、议一议
2、填空:绝对值最小的有理数是 ;绝对值最小的自然数是 ;绝对值最小的负整数是 。
0
0
-1
好好想想
1、利用数轴回答: ⑴有没有最大的整数和最小的整数?
⑶有没有最大的负整数和最小的负整数?
答:没有最大的正整数,最小的正整数是1。
答:都没有。
⑵有没有最大的正整数和最小的正整数?
答:最大的负整数是-1,没有最小的负整数。
更上一层楼
(2)若a>0,b<0,且|a|<|b|,则你能比较 a、 b、-a、-b这四个数的大小吗?
(1)小明在课外书上看到一道习题:“若a表示一个有理数,请比较a与-a的大小”,他觉得太简单了,马上就得出了a > -a的结论,他做得对吗?
分类讨论:
若a是正数,则a>-a;
若a是负数,则a<-a;
若a是零,则a=0。
答:b<-a < a <-b
拓展提高
1、有理数的大小比较有几条法则?
2、你觉得什么情况下运用法则比较简单,什么情况下利用数轴比较简单?说说你的想法?
课堂反思
回顾与反思
我们这节课学到了什么
比较有理数大小的方法
数轴法:
在数轴上表示的两个数,右边的数总比左边的大.
规律:
(1)正数都大于0, 负数都 小于0, 正数大于一切负数
(2)两个负数,绝对值大的反而小.
1.3 有理数的大小
复习导入
进入了有理数的世界,我们已经学习了哪些知识?
一起来回顾一下吧!
1、任意写出两位正数,在数轴上画出表示它们的点,看看较大的数与较小的数的对应点的位置有何关系?
2、生活常识告诉我们,1℃与-2℃哪个温度高?-1℃与0℃哪个温度高?这个关系在温度计上表现为怎样的情况?
即较大的数表示的点在较小的数表示的点的右侧。
即温度高表示的液面在温度低的上面。
生活中的数学
若小文比小强矮8cm,记着:-8cm;小冬比小强矮10cm,记着:-10cm. 小文和小冬比较,结果小文高,所以-8>-10。
考试的时候,被老师扣2分比被老师扣5分的分数要高,所以-2>-5。
这就说明负数间也是可以比较大小的!
我们规定铅球的质量超过标准质量的部分记为正,低于标准质量的部分记为负.现有四个铅球的记录分别为-5克,+4克,+2克,-2克。哪个铅球最重,哪个最轻?
生活中的数学
合肥在某冬日6时,14时,16时,23时的气温分别为-5℃ ,4 ℃ ,2 ℃和-2 ℃.哪个时刻的气温最高,哪个时刻的气温最低?
上述问题都可以归结为比较有理数“ -5,4,+2,-2 ”的大小.
活动探究1
某地一天中5个不同的时刻的气温分别是
- 2℃, -5℃, 4℃, 0℃,2 ℃.
10
10
5
5
0
0
-5
-5
-10
-10
-5
-2
4
0
单位:℃
(1)请你按照由低到高的顺序把不同时刻的气温排列出来。
-5℃<-2℃<0℃< 2 ℃ < 4℃
2
(2)观察不同温度在温度计上对应的颜色液面位置有什么关系
同一温度计上, 不同时刻显示的温度,液面高的总比液面低的表示的温度高.
10
10
5
5
0
0
-5
-5
-10
-10
把有理数 -3、-5、 4、 0、2表示在数轴上,这些数的大小与其在数轴上的点的位置有什么关系?
-5 -4 -3 -2 -1 0 1 2 3 4 5
-3
-5
4
0
活动探究2
2
-5℃<-3℃<0℃< 2 ℃ < 4℃
在数轴上表示的两个数,右边的数总比左边的数大。
正数都大于0,0大于负数,正数大于一切负数。
规律:
知识总结1
活动探究3
1、在数轴上表示下列各对数,并比较它们的大小;
⑴2和7; ⑵-6和-1;
⑶-2和-5; ⑷-2 和-1.5
2、求上述各对数的绝对值,并比较它们的大小。上面各对数的大小与他们的绝对值的大小有什么关系?
知识总结2
两个正数大小比较:
两个负数大小比较:
一正一负大小比较:
正数与零大小比较:
负数与零大小比较:
绝对值大的较大
绝对值大的反而小
正数大于负数
正数都大于零
负数都小于零
有理数大小比较法则:
1、在数轴上表示的两个数,右边的总比左边的数大。
2、正数都大于零,负数都小于零,正数大于负数。
3、两个正数比较大小,绝对值大的数较大;两个负
数比较大小,绝对值大的数反而小。
知识整理
例 比较下列每对数的大小,并说明理由:
(1)1与-10; (2)-0.001与0 (3)
解:
(1) 1>-10
(2)-0.001<0
(3)因为
(两个负数比较大小,绝对值大的数反而小)
所以
(正数大于一切负数)
(负数都小于零)
且
小试牛刀
1、(抢答)用“>”或“<”号填空:
(1)-6____-4
(3) 0_____-9
(4)
( 5 )
( 2 )
(6)-0.01___ 0.001
2、把下面各组数表示在数轴上,并按从小到大的顺序用“ < ”好号连接:
⑴-7,-3,-1; ⑵ 5,0,-4 ,-2,
3、比较下面各对数的大小,并说明理由:
⑴ 与 ; ⑵-3 与 +1;
⑶ -1 与 0; ⑷ - 与 -
4、利用数轴求出大于- 3.2并且小于3.2的整数。
小试牛刀
(1)有没有最小的正数?有没有最大的负数?
(2)有没有绝对值最小的有理数?若有,请把它写出来.
想一想、议一议
2、填空:绝对值最小的有理数是 ;绝对值最小的自然数是 ;绝对值最小的负整数是 。
0
0
-1
好好想想
1、利用数轴回答: ⑴有没有最大的整数和最小的整数?
⑶有没有最大的负整数和最小的负整数?
答:没有最大的正整数,最小的正整数是1。
答:都没有。
⑵有没有最大的正整数和最小的正整数?
答:最大的负整数是-1,没有最小的负整数。
更上一层楼
(2)若a>0,b<0,且|a|<|b|,则你能比较 a、 b、-a、-b这四个数的大小吗?
(1)小明在课外书上看到一道习题:“若a表示一个有理数,请比较a与-a的大小”,他觉得太简单了,马上就得出了a > -a的结论,他做得对吗?
分类讨论:
若a是正数,则a>-a;
若a是负数,则a<-a;
若a是零,则a=0。
答:b<-a < a <-b
拓展提高
1、有理数的大小比较有几条法则?
2、你觉得什么情况下运用法则比较简单,什么情况下利用数轴比较简单?说说你的想法?
课堂反思
回顾与反思
我们这节课学到了什么
比较有理数大小的方法
数轴法:
在数轴上表示的两个数,右边的数总比左边的大.
规律:
(1)正数都大于0, 负数都 小于0, 正数大于一切负数
(2)两个负数,绝对值大的反而小.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
