沪科版七年级上册数学 2.2.3整式加减 复习 课件(共21张PPT)
文档属性
| 名称 | 沪科版七年级上册数学 2.2.3整式加减 复习 课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 779.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-24 21:08:41 | ||
图片预览








文档简介
(共21张PPT)
第二章 整式的加减
小结复习
数学 七年级 上册
内容概要
本节课是第二章整式的加减小结复习课,本章的主要内容是:单项式、多项式、整式、同类项的概念;用字母列式表示数量关系,合并同类项法则,去括号法则以及整式的加减运算.
学习目标:
1.梳理整式的相关概念,归纳概念之间的区别与联系.
2.在正确合并同类项、准确运用去括号时的符号变化
规律的基础上,达到可以熟练地进行整式的加减运算.
3.进一步体会用字母表示数的意义,体会“数式通性”,
体会蕴含在具体问题中的数学思想和规律.
学习重难点:
概念之间的内在联系,以及可以熟练地进行整式的加减运算.
【问题1】本章学习了哪些知识?它们之间的联系是什么?
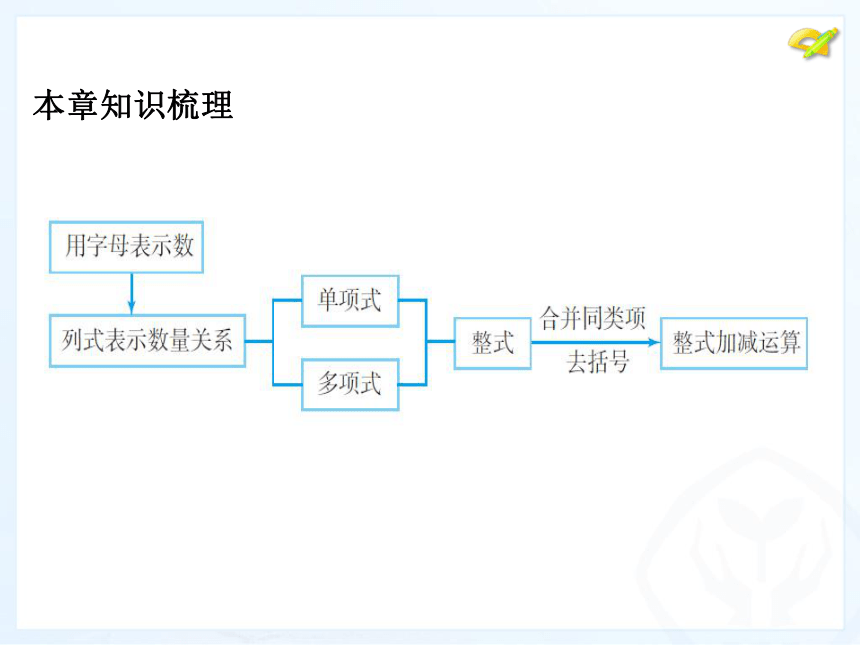
(一)知识梳理,把握重点
本章知识梳理
【问题2】在本章中,与整式相关的概念有哪些?
(二)典型分析,强调方法
例1 下列整式中哪些是单项式?哪些是多项式?是单项式的指出系数和次数,是多项式的指出项和多项式的次数。
x
32t3
x
32t3
1
32
1
3
6
3
1
4
2
3x2 , _y, +3xy3 ,x4 , -1
(1)单项式的次数是指所有字母的指数和,它仅与式子中的字母有关,只含有一个字母时,指数是1,指数1通常不写,所以x的次数是1;
(2)多项式是几个单项式的“和”,多项式的项是指“和”中的每一个单项式,多项式的项数就是指“和”中单项式的个数,包括其中的常数项;
(3)多项式的次数,是多项式里次数最高的项的次数.
应特别关注的是:
【问题3】你还记得怎样进行整式的加减运算吗?
(二)典型分析,强调方法
整式加减的一般步骤是:
(1)如果有括号,那么要先去括号;
(2)如果有同类项,合并同类项;
1.说出下列各组中的两个单项式是不是同类项?为什么?
(1)x2y与-3yx2; (2) a2b2与-ab2;
(3)-3与6; (4) 2a与ab
2. 指出4x2 - 8x + 5 - 3x2 - 6x - 2中的同类项
不是
是
不是
是
多项式中的项:
4x2 ,- 8x , + 5 ,- 3x2 , - 6x , - 2
同类项:
4x2与- 3x2
- 8x与- 6x
+ 5与- 2
1.已知: 与 是同类项,求 m、n的值 .
2
_
3
x3my3
-
1
_
4
x6yn+1
2.已知: 与 能合并.则 m= ,n= .
3.关于a, b的多项式
不ab含项. 则m= .
4.如果2a2bn+1与-4amb3是同类项,则m=___,n=__;
5.若5xy2+axy2=-2xy2,则a=____;
6.在6xy-3x2-4x2y-5yx2+x2中没有同类项的项是___
2 3
3
2 2
-7
6xy
练习(合并下列各式的同类项)
(1)-xy2– xy2
(2) – 3x2y - 3xy2 + 2x2y - 2xy2
1
__
5
(3)4a2+3b2+2ab-4a2-4b2
(4)m-n2+m-n2
下列各题合并同类项的结果对不对?若不对,请改正。
(1)、
(2)、
(3)、
(4)、
×
√
×
×
[例1]
若-5a3bm+1与8an+1b2是同类项,求(m-n)100的值。
解:由同类项的定义知:m+1=2,n+1=3;解得m=1,n=2
∴(m-n)100=(1-2)100=(-1)100=1
答:当m=1,n=2时,(m-n)100=1。
评析:例1要注意同类项概念的应用;例2要注意几位数的表示方法。如:578=5×100+7×10+8。
[例2]如果一个两位数的个位数是十位数的4倍,那么这个两位数一定是7的倍数。请说明理由。
解:设两位数的十位数字是x,则它的个位数字是4x。
∴这个两位数可表示为:10x+4x=14x,
∵14x是7的倍数,故这个两位数是7的倍数。
1、去括号是本章的难点之一;去括号都是多项式的恒等变形;去括号时一定对照法则把去掉括号与括号的符号看成统一体,不能拆开。
法则:如果括号外的因数是正数,去括号后原括号内的各项的符号与原来的符号( );
如果括号外的因数是负数,去括号后原括号内的各项的符号与原来的符号( )。
去括号的法则:添括号去括号,
都要看符号;
负变正不变,
要变一起变,
不变都不变。
相同
相反
【问题4】运用本章所学习的内容,可解决哪些问题?
(二)典型分析,强调方法
[练习]
2.已知a2-ab=2,4ab-3b2=-3,试求a2-13ab+9b2-5的值。
1.化简求值:3x2-[7x-(4x-3)-2x3],其中x=-0.5
3.某人做了一道题:
“一个多项式减去3x2-5x+1…”,他误将减去3x2-5x+1写为加上3x2-5x+1,得出的结果是5x2+3x-7。求出这道题的正确结果。
提示:a2-13ab+9b2-5=(a2-ab)-3(4ab-3b2)-5
答案:-1
提示:先设被减数为A,可由已知求出多项式A,再计算A-(3x2-5x+1)
(三)课堂小结,归纳提升
应特别关注的是:
(1)对整式及其相关概念“是什么”、“之间有哪些联系”、“有什么用”等方面的认识是否有所提高;
(2)是否更加清晰地认识到进行整式的加减实际上就是将整式化简,而化简的主要方法是合并多项式中的同类项和去括号.
第二章 整式的加减
小结复习
数学 七年级 上册
内容概要
本节课是第二章整式的加减小结复习课,本章的主要内容是:单项式、多项式、整式、同类项的概念;用字母列式表示数量关系,合并同类项法则,去括号法则以及整式的加减运算.
学习目标:
1.梳理整式的相关概念,归纳概念之间的区别与联系.
2.在正确合并同类项、准确运用去括号时的符号变化
规律的基础上,达到可以熟练地进行整式的加减运算.
3.进一步体会用字母表示数的意义,体会“数式通性”,
体会蕴含在具体问题中的数学思想和规律.
学习重难点:
概念之间的内在联系,以及可以熟练地进行整式的加减运算.
【问题1】本章学习了哪些知识?它们之间的联系是什么?
(一)知识梳理,把握重点
本章知识梳理
【问题2】在本章中,与整式相关的概念有哪些?
(二)典型分析,强调方法
例1 下列整式中哪些是单项式?哪些是多项式?是单项式的指出系数和次数,是多项式的指出项和多项式的次数。
x
32t3
x
32t3
1
32
1
3
6
3
1
4
2
3x2 , _y, +3xy3 ,x4 , -1
(1)单项式的次数是指所有字母的指数和,它仅与式子中的字母有关,只含有一个字母时,指数是1,指数1通常不写,所以x的次数是1;
(2)多项式是几个单项式的“和”,多项式的项是指“和”中的每一个单项式,多项式的项数就是指“和”中单项式的个数,包括其中的常数项;
(3)多项式的次数,是多项式里次数最高的项的次数.
应特别关注的是:
【问题3】你还记得怎样进行整式的加减运算吗?
(二)典型分析,强调方法
整式加减的一般步骤是:
(1)如果有括号,那么要先去括号;
(2)如果有同类项,合并同类项;
1.说出下列各组中的两个单项式是不是同类项?为什么?
(1)x2y与-3yx2; (2) a2b2与-ab2;
(3)-3与6; (4) 2a与ab
2. 指出4x2 - 8x + 5 - 3x2 - 6x - 2中的同类项
不是
是
不是
是
多项式中的项:
4x2 ,- 8x , + 5 ,- 3x2 , - 6x , - 2
同类项:
4x2与- 3x2
- 8x与- 6x
+ 5与- 2
1.已知: 与 是同类项,求 m、n的值 .
2
_
3
x3my3
-
1
_
4
x6yn+1
2.已知: 与 能合并.则 m= ,n= .
3.关于a, b的多项式
不ab含项. 则m= .
4.如果2a2bn+1与-4amb3是同类项,则m=___,n=__;
5.若5xy2+axy2=-2xy2,则a=____;
6.在6xy-3x2-4x2y-5yx2+x2中没有同类项的项是___
2 3
3
2 2
-7
6xy
练习(合并下列各式的同类项)
(1)-xy2– xy2
(2) – 3x2y - 3xy2 + 2x2y - 2xy2
1
__
5
(3)4a2+3b2+2ab-4a2-4b2
(4)m-n2+m-n2
下列各题合并同类项的结果对不对?若不对,请改正。
(1)、
(2)、
(3)、
(4)、
×
√
×
×
[例1]
若-5a3bm+1与8an+1b2是同类项,求(m-n)100的值。
解:由同类项的定义知:m+1=2,n+1=3;解得m=1,n=2
∴(m-n)100=(1-2)100=(-1)100=1
答:当m=1,n=2时,(m-n)100=1。
评析:例1要注意同类项概念的应用;例2要注意几位数的表示方法。如:578=5×100+7×10+8。
[例2]如果一个两位数的个位数是十位数的4倍,那么这个两位数一定是7的倍数。请说明理由。
解:设两位数的十位数字是x,则它的个位数字是4x。
∴这个两位数可表示为:10x+4x=14x,
∵14x是7的倍数,故这个两位数是7的倍数。
1、去括号是本章的难点之一;去括号都是多项式的恒等变形;去括号时一定对照法则把去掉括号与括号的符号看成统一体,不能拆开。
法则:如果括号外的因数是正数,去括号后原括号内的各项的符号与原来的符号( );
如果括号外的因数是负数,去括号后原括号内的各项的符号与原来的符号( )。
去括号的法则:添括号去括号,
都要看符号;
负变正不变,
要变一起变,
不变都不变。
相同
相反
【问题4】运用本章所学习的内容,可解决哪些问题?
(二)典型分析,强调方法
[练习]
2.已知a2-ab=2,4ab-3b2=-3,试求a2-13ab+9b2-5的值。
1.化简求值:3x2-[7x-(4x-3)-2x3],其中x=-0.5
3.某人做了一道题:
“一个多项式减去3x2-5x+1…”,他误将减去3x2-5x+1写为加上3x2-5x+1,得出的结果是5x2+3x-7。求出这道题的正确结果。
提示:a2-13ab+9b2-5=(a2-ab)-3(4ab-3b2)-5
答案:-1
提示:先设被减数为A,可由已知求出多项式A,再计算A-(3x2-5x+1)
(三)课堂小结,归纳提升
应特别关注的是:
(1)对整式及其相关概念“是什么”、“之间有哪些联系”、“有什么用”等方面的认识是否有所提高;
(2)是否更加清晰地认识到进行整式的加减实际上就是将整式化简,而化简的主要方法是合并多项式中的同类项和去括号.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
