人教A版(2019)数学必修第一册期末复习:同角三角函数的基本关系与诱导公式 课件(共40张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第一册期末复习:同角三角函数的基本关系与诱导公式 课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 00:00:00 | ||
图片预览



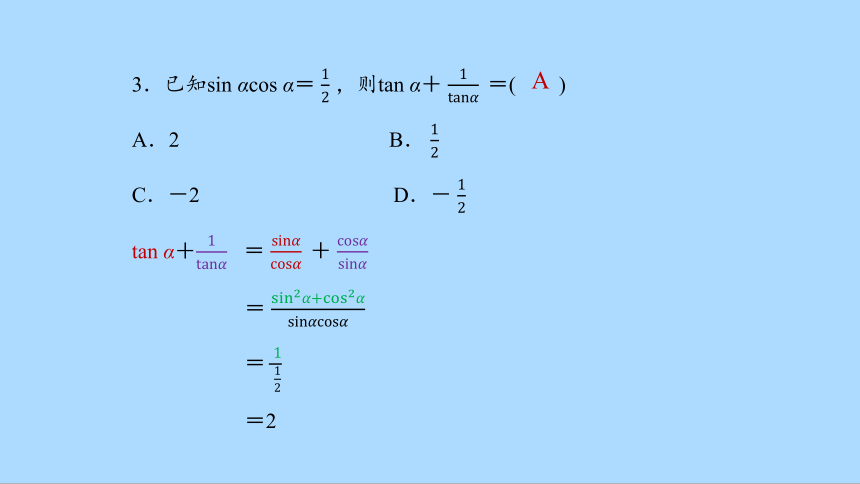
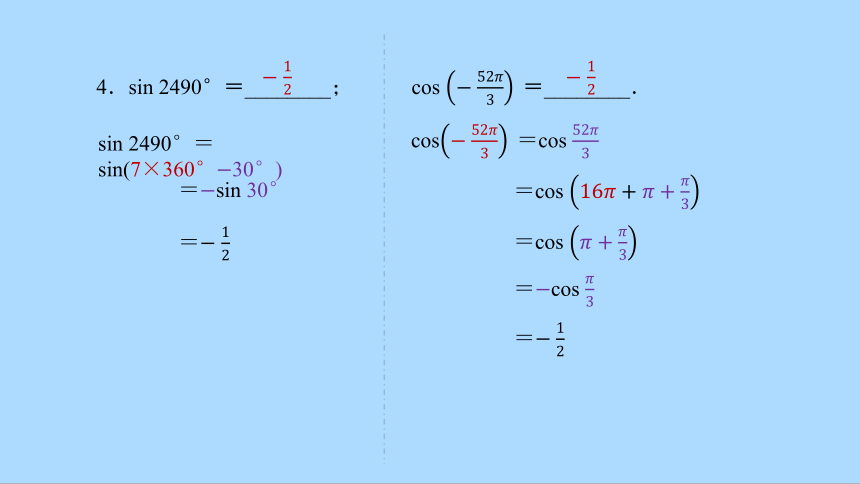




文档简介
(共40张PPT)
同角三角函数的基本关系与诱导公式
考纲分析
课程标准解读 关联考点 核心素养
1.理解同角三角函数的基本关系式:sin2x+cos2x=1,=tan x. 2.借助单位圆及三角函数的定义推导出诱导公式. (,的正弦、余弦、正切) 1.同角三角函数基本关系式的应用. 2.诱导公式的应用. 3.诱导公式与同角关系的综合应用. 1.数学运算.
2.逻辑推理.
课前自测
(4)若cos(nπ-θ)= (n∈Z),则cos θ=.( )
1.判断正误(正确的打“√”,错误的打“×”)
(1)对任意的角α,β,都有sin2α+cos2β=1.( )
(2)若α∈R,则tan α= 恒成立.( )
(3)sin(π+α)=-sin α成立的条件是α为锐角.( )
×
×
×
×
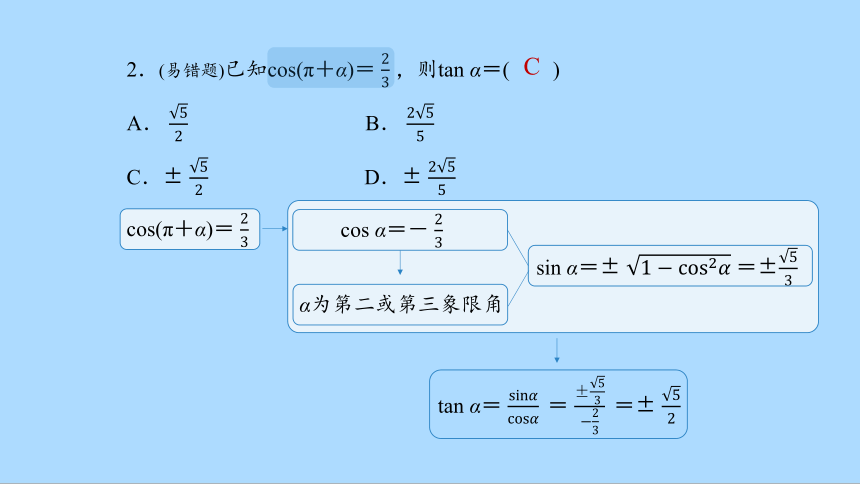
2.(易错题)已知cos(π+α)= ,则tan α=( )
A. B.
C.± D.±
cos(π+α)=
cos α=-
α为第二或第三象限角
sin α=± =±
tan α= = =±
C
3.已知sin αcos α= ,则tan α+ =( )
A.2 B.
C.-2 D.-
=
tan α+
= +
=
=2
A
4.sin 2490°=________; cos =________.
sin 2490°=sin(7×360°30°)
=sin 30°
=
cos=cos
=cos
=cos
=cos
=
5.化简·cos(2π-α)的结果为________.
·cos(2π-α)
= ·cos α
=sin α
sin α
考点梳理
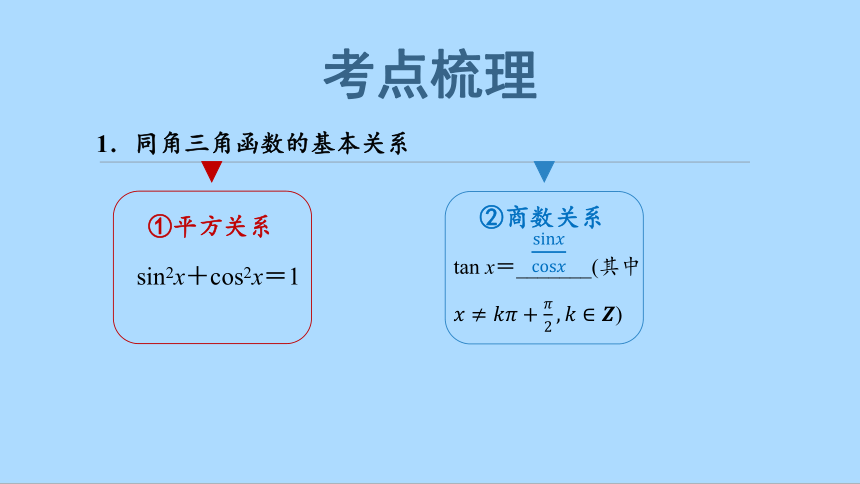
1.同角三角函数的基本关系
①平方关系
sin2x+cos2x=1
②商数关系
tan x=_______(其中)
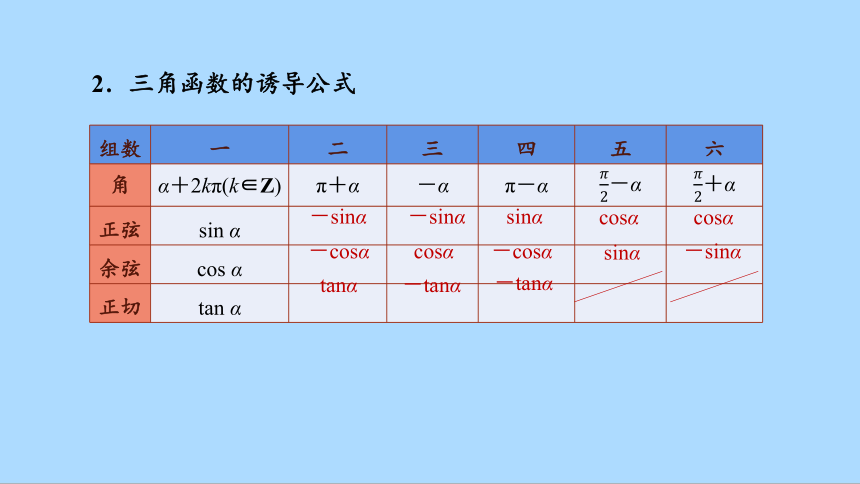
2.三角函数的诱导公式
组数 一 二 三 四 五 六
角 α+2kπ(k∈Z) π+α -α π-α -α +α
正弦 sin α
余弦 cos α
正切 tan α
-sinα
-cosα
tanα
-sinα
cosα
-tanα
sinα
-cosα
-tanα
cosα
sinα
cosα
-sinα
常用结论
1.诱导公式的记忆口诀
其中的奇、偶是指的奇数倍和偶数倍,变与不变指函数名称的变化.
“奇变偶不变,符号看象限”
2.同角三角函数的基本关系式的几种变形
(1) sin2α=1-cos2α=(1+cos α)(1-cos α);
cos2α=1-sin2α=(1+sin α)(1-sin α);
(sin α±cos α)2=1±2sin αcos α.
(2) sin α=tan αcos α ().
cos2α= = .
(3) sin2α= = ;
常见误区
1.同角三角函数的基本关系式及诱导公式要注意角的范围对三角函数符号的影响,尤其是利用平方关系求三角函数值,进行开方时要根据角的范围,判断符号后,正确取舍.
!
2.注意求值与化简后的结果一般要尽可能有理化、整式化.
典例剖析
考点
1
同角三角函数的基本关系式
角度一 “知一求二”问题
[例1] (2020·北京市适应性测试)已知α是第四象限角,且tan α=-,则sin α=( )
A.- B. C. D.-
A
tan α= =-
cos α=-sin α
sin2α+cos2α=1
sin2α=
α是第四象限角
sin α<0
sin α=-
方法总结
利用同角三角函数的基本关系求解问题的关键是熟练掌握同角三角函数的基本关系的正用、逆用、变形.同角三角函数的基本关系本身是恒等式,也可以看作是方程,对于一些题,可利用已知条件,结合同角三角函数的基本关系列方程组,通过解方程组达到解决问题的目的.
角度二 sin α,cos α的齐次式问题
[例2] 已知=-1,求下列各式的值:
(2)sin2α+sin αcos α+2.
(1) ;
tan α=
=
=-
sin2α+sin αcos α+2= +2
= +2
= +2
=
方法总结
已知tan α,求关于sin α与cos α的齐n次分式或齐二次整式的值.
关于sin α与cos α的齐n次分式或齐二次整式的化简求值的解题策略
角度三 sin α±cos α,sin αcos α之间的关系
[例3] 已知α∈(-π,0),sin α+cos α= .
(1)求sin α-cos α的值;
sin α+cos α=
α∈(-π,0)
sin2α+2sin αcos α+cos2α=
2sin αcos α=-
(sin α-cos α)2=1-2sin αcos α=
sin α<0
sin α+cos α>0
cos α>0
sin α-cos α<0
sin α-cos α=-
角度三 sin α±cos α,sin αcos α之间的关系
[例3] 已知α∈(-π,0),sin α+cos α= .
(2)求的值.
方法总结
sin α±cos α与sin αcos α关系的应用技巧
(1)通过平方,sin α+cos α,sin α-cos α,sin αcos α之间可建立联系,若令sin α+cos α=t,则sin αcos α= ,sin α-cos α=± (注意根据α的范围选取正、负号).
(2)对于sin α+cos α,sin α-cos α,sin αcos α这三个式子,可以知一求二.
跟踪训练
1.(2020·河南六市一模)已知cos = ,且α∈,则tan α=( )
A. B. C.- D.±
cos=
sin α=-
α∈
cos α=- =-
tan α= =
B
2.已知tan α=- ,则sin α(sin α-cos α)=( )
A. B. C. D.
将tan α=-代入得原式= = .
sin α(sin α-cos α)=sin2α-sin αcos α
=
=
A
3.(一题多解)已知sin α-cos α=,α∈(0,π),则tan α=( )
A.-1 B.- C. D.1
法一
所以tan α=tan =-1.
由
得2cos2α+2cos α+1=0,即(cos α+1)2=0,
所以cos α=-.
又α∈(0,π),所以α= ,
A
3.(一题多解)已知sin α-cos α=,α∈(0,π),则tan α=( )
A.-1 B.- C. D.1
法二
A
sin α-cos α=
sin =
sin =1
α∈(0,π)
α=
tan α=-1
3.(一题多解)已知sin α-cos α=,α∈(0,π),则tan α=( )
A.-1 B.- C. D.1
法三
A
sin α-cos α=
1-sin 2α=2
sin 2α=-1
设sin α+cos α=t
1+sin 2α=t2
t=0
sin α= ,cos α=-
tan α=-1
考点
2
诱导公式的应用
[例4] (1)sin(-1200°)cos 1290°=________.
=sin 60°cos 30°
原式=-sin 1200°cos 1290°
=-sin(3×360°+120°) cos(3×360°+210°)
=-sin 120°cos 210°
=-sin(180°-60°)cos(180°+30°)
= × = .
考点
2
诱导公式的应用
由题意可知tan θ=3,
原式=
=
=
=
(2)已知角θ的顶点在坐标原点,始边与x轴正半轴重合,终边在直线3x-y=0上,则等于________.
变式探究
(变问法)若本例(2)的条件不变,则=________.
= = =3.
(2)已知角θ的顶点在坐标原点,始边与x轴正半轴重合,终边在直线3x-y=0上,则等于________.
由题意可知tan θ=3,
原式=
=
=
3
方法总结
②常见的互补的角: +θ与-θ; +θ与-θ等.
(1)诱导公式用法的一般思路
①化负为正,化大为小,化到锐角为止;
②角中含有加减的整数倍时,用公式去掉的整数倍.
(2)常见的互余和互补的角
①常见的互余的角: -α与+α; +α与-α; +α与-α等;
跟踪训练
1.已知sin = ,则cos 的值是( )
A.- B. C. D.-
cos = cos
=sin
=
A
2.(多选)已知A= ,则A的值可以是( )
A.3 B.-3 C.1 D.-1
A= = + + =-1,
A= = + + =3;
当k为偶数时,
当k为奇数时,
所以A的值可以是3或-1.
AD
考点
3
同角三角函数的基本关系式与诱导公式的综合应用
[例5] (2020·湖北宜昌一中期末)已知α是第三象限角,且cos α=- .
(1)求tan α的值;
(2)化简并求的值.
由(1)知tan α=3,所以原式= = .
(1)
(2)原式= = = ,
α是第三象限角
cos α=-
sin α=- =-
tan α= =3
方法总结
求解诱导公式与同角关系综合问题的基本思路和化简要求
基本 思路 ①分析结构特点,选择恰当公式;
②利用公式化成单角三角函数;
③整理得最简形式
化简 要求 ①化简过程是恒等变换;
②结果要求项数尽可能少,次数尽可能低,结构尽可能简单,能求值的要求出值
跟踪训练
1.已知sin = ,所以tan α的值为( )
A.- B.- C.± D.±
sin =sin
=cos
=
sin
tan α
C
2.已知tan(π-α)=- ,且α∈ ,则的值为( )
A.- B.- C. D.
所以=
A
因为tan(π-α)=-,所以tan α=,
=
=
=-
随堂训练
1.已知角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边上一点A(2sin α,3)(sin α≠0),则cos α=( )
A. B.- C. D.-
由三角函数定义得tan α= ,
即= ,
得3cos α=2sin2α=2(1-cos2α),
解得cos α= 或cos α=-2(舍去).
A
2.计算:sin +cos 的值为________.
=- -
原式=sin(2)+cos ()
=-sin -cos
=-1
-1
3.已知sin cos = ,且0<α< ,则sin α=________,cos α=________.
又因为sin2α+cos2α=1,
sin cos =-cos α·(-sin α)=sin αcos α= .
因为0<α< ,所以0<sin α<cos α.
所以sin α= ,cos α= .
4.化简=________.
=
原式=
=
=
=1.
1
5.已知sin(3π+α)=2sin ,求下列各式的值:
(1) ; (2)sin2α+sin 2α.
(2)原式= = = .
sin(3π+α)=2sin
sin α=2cos α
(1)原式= =-.
本课小结
本节知识主要考查利用同角三角函数的基本关系、诱导公式解决条件求值问题,常与三角恒等变换相结合起到化简三角函数关系的作用,强调利用三角公式进行恒等变形的技巧以及基本的运算能力.
同角三角函数的基本关系与诱导公式
考纲分析
课程标准解读 关联考点 核心素养
1.理解同角三角函数的基本关系式:sin2x+cos2x=1,=tan x. 2.借助单位圆及三角函数的定义推导出诱导公式. (,的正弦、余弦、正切) 1.同角三角函数基本关系式的应用. 2.诱导公式的应用. 3.诱导公式与同角关系的综合应用. 1.数学运算.
2.逻辑推理.
课前自测
(4)若cos(nπ-θ)= (n∈Z),则cos θ=.( )
1.判断正误(正确的打“√”,错误的打“×”)
(1)对任意的角α,β,都有sin2α+cos2β=1.( )
(2)若α∈R,则tan α= 恒成立.( )
(3)sin(π+α)=-sin α成立的条件是α为锐角.( )
×
×
×
×
2.(易错题)已知cos(π+α)= ,则tan α=( )
A. B.
C.± D.±
cos(π+α)=
cos α=-
α为第二或第三象限角
sin α=± =±
tan α= = =±
C
3.已知sin αcos α= ,则tan α+ =( )
A.2 B.
C.-2 D.-
=
tan α+
= +
=
=2
A
4.sin 2490°=________; cos =________.
sin 2490°=sin(7×360°30°)
=sin 30°
=
cos=cos
=cos
=cos
=cos
=
5.化简·cos(2π-α)的结果为________.
·cos(2π-α)
= ·cos α
=sin α
sin α
考点梳理
1.同角三角函数的基本关系
①平方关系
sin2x+cos2x=1
②商数关系
tan x=_______(其中)
2.三角函数的诱导公式
组数 一 二 三 四 五 六
角 α+2kπ(k∈Z) π+α -α π-α -α +α
正弦 sin α
余弦 cos α
正切 tan α
-sinα
-cosα
tanα
-sinα
cosα
-tanα
sinα
-cosα
-tanα
cosα
sinα
cosα
-sinα
常用结论
1.诱导公式的记忆口诀
其中的奇、偶是指的奇数倍和偶数倍,变与不变指函数名称的变化.
“奇变偶不变,符号看象限”
2.同角三角函数的基本关系式的几种变形
(1) sin2α=1-cos2α=(1+cos α)(1-cos α);
cos2α=1-sin2α=(1+sin α)(1-sin α);
(sin α±cos α)2=1±2sin αcos α.
(2) sin α=tan αcos α ().
cos2α= = .
(3) sin2α= = ;
常见误区
1.同角三角函数的基本关系式及诱导公式要注意角的范围对三角函数符号的影响,尤其是利用平方关系求三角函数值,进行开方时要根据角的范围,判断符号后,正确取舍.
!
2.注意求值与化简后的结果一般要尽可能有理化、整式化.
典例剖析
考点
1
同角三角函数的基本关系式
角度一 “知一求二”问题
[例1] (2020·北京市适应性测试)已知α是第四象限角,且tan α=-,则sin α=( )
A.- B. C. D.-
A
tan α= =-
cos α=-sin α
sin2α+cos2α=1
sin2α=
α是第四象限角
sin α<0
sin α=-
方法总结
利用同角三角函数的基本关系求解问题的关键是熟练掌握同角三角函数的基本关系的正用、逆用、变形.同角三角函数的基本关系本身是恒等式,也可以看作是方程,对于一些题,可利用已知条件,结合同角三角函数的基本关系列方程组,通过解方程组达到解决问题的目的.
角度二 sin α,cos α的齐次式问题
[例2] 已知=-1,求下列各式的值:
(2)sin2α+sin αcos α+2.
(1) ;
tan α=
=
=-
sin2α+sin αcos α+2= +2
= +2
= +2
=
方法总结
已知tan α,求关于sin α与cos α的齐n次分式或齐二次整式的值.
关于sin α与cos α的齐n次分式或齐二次整式的化简求值的解题策略
角度三 sin α±cos α,sin αcos α之间的关系
[例3] 已知α∈(-π,0),sin α+cos α= .
(1)求sin α-cos α的值;
sin α+cos α=
α∈(-π,0)
sin2α+2sin αcos α+cos2α=
2sin αcos α=-
(sin α-cos α)2=1-2sin αcos α=
sin α<0
sin α+cos α>0
cos α>0
sin α-cos α<0
sin α-cos α=-
角度三 sin α±cos α,sin αcos α之间的关系
[例3] 已知α∈(-π,0),sin α+cos α= .
(2)求的值.
方法总结
sin α±cos α与sin αcos α关系的应用技巧
(1)通过平方,sin α+cos α,sin α-cos α,sin αcos α之间可建立联系,若令sin α+cos α=t,则sin αcos α= ,sin α-cos α=± (注意根据α的范围选取正、负号).
(2)对于sin α+cos α,sin α-cos α,sin αcos α这三个式子,可以知一求二.
跟踪训练
1.(2020·河南六市一模)已知cos = ,且α∈,则tan α=( )
A. B. C.- D.±
cos=
sin α=-
α∈
cos α=- =-
tan α= =
B
2.已知tan α=- ,则sin α(sin α-cos α)=( )
A. B. C. D.
将tan α=-代入得原式= = .
sin α(sin α-cos α)=sin2α-sin αcos α
=
=
A
3.(一题多解)已知sin α-cos α=,α∈(0,π),则tan α=( )
A.-1 B.- C. D.1
法一
所以tan α=tan =-1.
由
得2cos2α+2cos α+1=0,即(cos α+1)2=0,
所以cos α=-.
又α∈(0,π),所以α= ,
A
3.(一题多解)已知sin α-cos α=,α∈(0,π),则tan α=( )
A.-1 B.- C. D.1
法二
A
sin α-cos α=
sin =
sin =1
α∈(0,π)
α=
tan α=-1
3.(一题多解)已知sin α-cos α=,α∈(0,π),则tan α=( )
A.-1 B.- C. D.1
法三
A
sin α-cos α=
1-sin 2α=2
sin 2α=-1
设sin α+cos α=t
1+sin 2α=t2
t=0
sin α= ,cos α=-
tan α=-1
考点
2
诱导公式的应用
[例4] (1)sin(-1200°)cos 1290°=________.
=sin 60°cos 30°
原式=-sin 1200°cos 1290°
=-sin(3×360°+120°) cos(3×360°+210°)
=-sin 120°cos 210°
=-sin(180°-60°)cos(180°+30°)
= × = .
考点
2
诱导公式的应用
由题意可知tan θ=3,
原式=
=
=
=
(2)已知角θ的顶点在坐标原点,始边与x轴正半轴重合,终边在直线3x-y=0上,则等于________.
变式探究
(变问法)若本例(2)的条件不变,则=________.
= = =3.
(2)已知角θ的顶点在坐标原点,始边与x轴正半轴重合,终边在直线3x-y=0上,则等于________.
由题意可知tan θ=3,
原式=
=
=
3
方法总结
②常见的互补的角: +θ与-θ; +θ与-θ等.
(1)诱导公式用法的一般思路
①化负为正,化大为小,化到锐角为止;
②角中含有加减的整数倍时,用公式去掉的整数倍.
(2)常见的互余和互补的角
①常见的互余的角: -α与+α; +α与-α; +α与-α等;
跟踪训练
1.已知sin = ,则cos 的值是( )
A.- B. C. D.-
cos = cos
=sin
=
A
2.(多选)已知A= ,则A的值可以是( )
A.3 B.-3 C.1 D.-1
A= = + + =-1,
A= = + + =3;
当k为偶数时,
当k为奇数时,
所以A的值可以是3或-1.
AD
考点
3
同角三角函数的基本关系式与诱导公式的综合应用
[例5] (2020·湖北宜昌一中期末)已知α是第三象限角,且cos α=- .
(1)求tan α的值;
(2)化简并求的值.
由(1)知tan α=3,所以原式= = .
(1)
(2)原式= = = ,
α是第三象限角
cos α=-
sin α=- =-
tan α= =3
方法总结
求解诱导公式与同角关系综合问题的基本思路和化简要求
基本 思路 ①分析结构特点,选择恰当公式;
②利用公式化成单角三角函数;
③整理得最简形式
化简 要求 ①化简过程是恒等变换;
②结果要求项数尽可能少,次数尽可能低,结构尽可能简单,能求值的要求出值
跟踪训练
1.已知sin = ,所以tan α的值为( )
A.- B.- C.± D.±
sin =sin
=cos
=
sin
tan α
C
2.已知tan(π-α)=- ,且α∈ ,则的值为( )
A.- B.- C. D.
所以=
A
因为tan(π-α)=-,所以tan α=,
=
=
=-
随堂训练
1.已知角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边上一点A(2sin α,3)(sin α≠0),则cos α=( )
A. B.- C. D.-
由三角函数定义得tan α= ,
即= ,
得3cos α=2sin2α=2(1-cos2α),
解得cos α= 或cos α=-2(舍去).
A
2.计算:sin +cos 的值为________.
=- -
原式=sin(2)+cos ()
=-sin -cos
=-1
-1
3.已知sin cos = ,且0<α< ,则sin α=________,cos α=________.
又因为sin2α+cos2α=1,
sin cos =-cos α·(-sin α)=sin αcos α= .
因为0<α< ,所以0<sin α<cos α.
所以sin α= ,cos α= .
4.化简=________.
=
原式=
=
=
=1.
1
5.已知sin(3π+α)=2sin ,求下列各式的值:
(1) ; (2)sin2α+sin 2α.
(2)原式= = = .
sin(3π+α)=2sin
sin α=2cos α
(1)原式= =-.
本课小结
本节知识主要考查利用同角三角函数的基本关系、诱导公式解决条件求值问题,常与三角恒等变换相结合起到化简三角函数关系的作用,强调利用三角公式进行恒等变形的技巧以及基本的运算能力.
同课章节目录
