3.3.2课时1:抛物线的简单几何性质- 2022-2023学年高二数学人教A版(2019)选择性必修一同步练习(含答案)
文档属性
| 名称 | 3.3.2课时1:抛物线的简单几何性质- 2022-2023学年高二数学人教A版(2019)选择性必修一同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 464.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 09:57:37 | ||
图片预览




文档简介
3.3.2课时1:抛物线的简单几何性质
若抛物线上一点到焦点和到抛物线对称轴的距离分别为和,则抛物线的方程为( )
A. B.
C. 或 D. 或
已知抛物线的焦点为,为抛物线上一动点,,则的周长最小值为( )
A. B. C. D.
已知抛物线:上的点到的焦点的距离为,点在直线上的射影为,点关于轴的对称点为,则四边形的周长为( )
A. B. C. D.
已知抛物线:的焦点为,直线与抛物线交于,两点,若的中点的纵坐标为,则( )
A. B. C. D.
如图所示,点是抛物线的焦点,点,分别在抛物线及圆的实线部分上运动,且总是平行于轴,则的周长的取值范围是( )
A. B. C. D.
已知双曲线:的右顶点到其一条渐近线的距离等于,抛物线:的焦点与双曲线的右焦点重合,则抛物线上的动点到直线:和:的距离之和的最小值为( )
A. B. C. D.
已知拋物线的焦点为,点为拋物线上位于第一象限内一点,若且直线的斜率为,则拋物线的方程为( )
A. B. C. D.
点到抛物线的准线的距离为,则的值可以为( )
A. B. C. D.
已知抛物线的焦点为,是抛物线上两动点,是平面内一定点,下列说法正确的有( )
A. 准线方程为
B. 若,则线段中点到轴为
C. 的周长的最小值为
D. 以线段为直径的圆与准线相切
若抛物线上一点到其准线的距离为,则抛物线的标准方程为 .
某抛物线拱桥的跨度是米,中间拱高是米,在建桥时每隔米需用一支柱支撑,其中最长的支柱高是 米
设抛物线的焦点为,准线为,已知点在上,以为圆心的圆与轴的正半轴相切于点,若,则圆的方程为 .
在平面直角坐标系中,抛物线的焦点为,准线为,过抛物线上一点作的垂线,垂足为,与相交于点若,且的面积为,则的值为
点,抛物线的焦点为,若对于抛物线上的任意点,的最小值为,则的值等于 .
给出下列命题:
到定点与定直线的距离相等的点的轨迹是抛物线;
设为两个定点,为常数且,若,则动点的轨迹是双曲线。
对任意实数,直线总与某一个定圆相切。
在平面内,到两定点的距离的和等于常数的点的轨迹是椭圆;
方程的两根可分别作为椭圆和双曲线的离心率.
其中真命题的序号是 把你认为正确的命题的序号都填上。
求适合下列条件的曲线标准方程.
虚轴长为,离心率为的双曲线的标准方程;
过点的抛物线的标准方程.
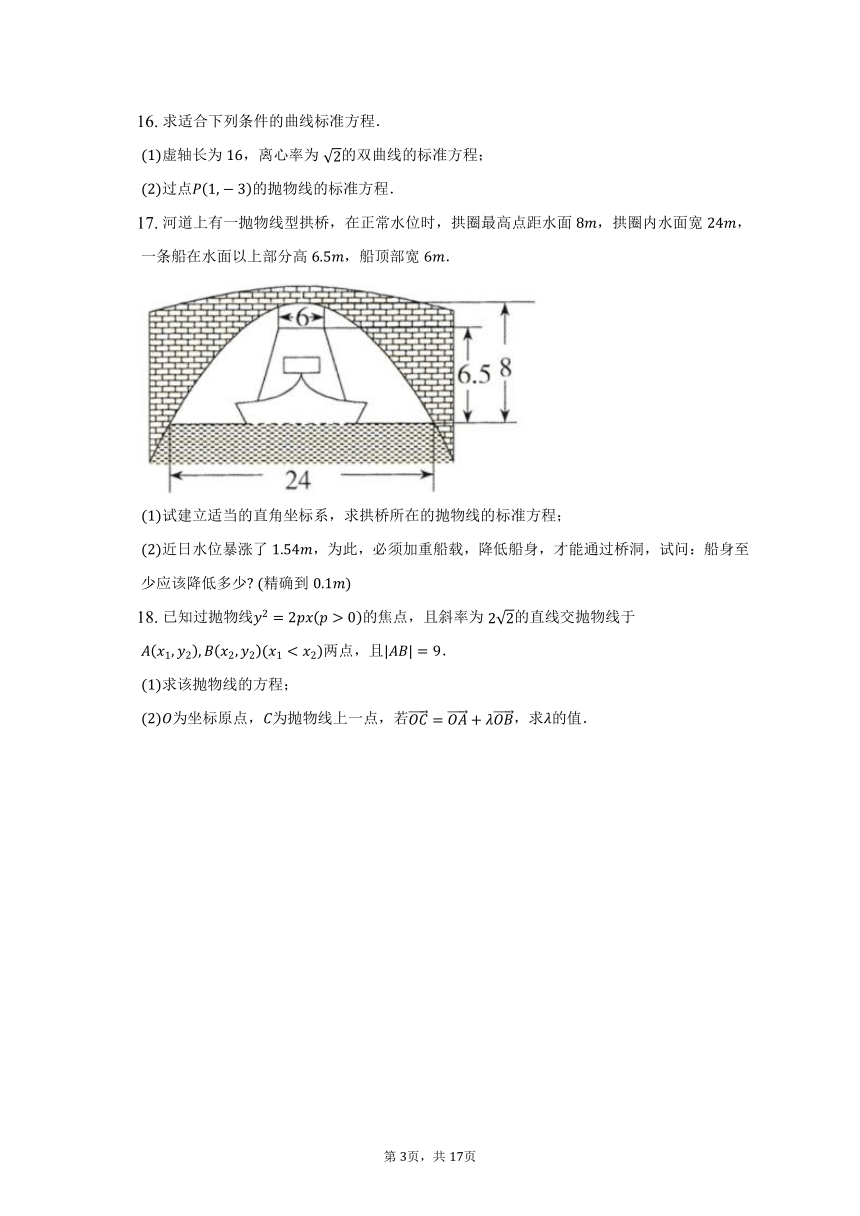
河道上有一抛物线型拱桥,在正常水位时,拱圈最高点距水面,拱圈内水面宽,一条船在水面以上部分高,船顶部宽.
试建立适当的直角坐标系,求拱桥所在的抛物线的标准方程;
近日水位暴涨了,为此,必须加重船载,降低船身,才能通过桥洞,试问:船身至少应该降低多少 精确到
已知过抛物线的焦点,且斜率为的直线交抛物线于两点,且.
求该抛物线的方程;
为坐标原点,为抛物线上一点,若,求的值.
答案和解析
1.【答案】
【解析】
【分析】
由抛物线上点到抛物线对称轴的距离为,设该点为根据点坐标适合抛物线方程及点到焦点的距离为,列方程组,解之可得与的值,从而得到本题的答案.
本题已知抛物线上一点到焦点和到抛物线对称轴的距离,求抛物线的焦参数,着重考查了抛物线的标准方程与简单几何性质等知识,属于基础题.
【解答】
解:抛物线上一点到抛物线对称轴的距离为,
设该点为,则的坐标为
到抛物线的焦点的距离为
由抛物线的定义,得
点是抛物线上的点,
由联立,解得,或,
则抛物线方程为或.
故选:.
2.【答案】
【解析】
【分析】
本题考查抛物线的简单性质,考查数形结合思想,属于基础题.
由题意画出图形,过作准线的垂线,交抛物线于,则此时的周长最小,然后结合两点间的距离公式即可求解.
【解答】
解:如图,
抛物线:的焦点为,准线方程为.
过作准线的垂线,交抛物线于,则的周长最小.
最小值为.
故选:.
3.【答案】
【解析】
【分析】
本题考查抛物线的定义以及几何性质的应用,属于基础题.
根据题意可得四边形为直角梯形,结合抛物线的定义可得,再得出、,即可求四边形的周长.
【解答】
解:由抛物线的方程可知,,直线为抛物线的准线,
所以,四边形为直角梯形.
因为,所以根据抛物线的定义,得,
过点作轴于点,则,
在中,,
所以四边形的周长为,
故选B.
4.【答案】
【解析】
【分析】
本题主要考查了抛物线性质的应用,直线与抛物线的位置关系,属于基础题.
由抛物线的定义,得,根据中点的坐标公式,得,代入即可求解.
【解答】
解:由抛物线:可知,,得到,,
设,,因为的中点的纵坐标为,
所以,则.
故选C.
5.【答案】
【解析】
【分析】
本题考查抛物线的定义,考查抛物线与圆的位置关系,属于中档题.
由抛物线定义可得,从而的周长,确定点横坐标的范围,即可得到结论.
【解答】
解:抛物线的准线:,焦点,
由抛物线定义可得,
圆的圆心为,半径为,
的周长
,
由抛物线及圆可得交点的横坐标为,
,
,
故选B.
6.【答案】
【解析】
【分析】
本题考查双曲线的方程,主要是渐近线方程的运用,同时考查抛物线的方程,属于较难题.
求出双曲线的渐近线方程,运用点到直线的距离公式计算可得,进而得到,可得,进而得到抛物线的方程.连接,过点作于点,作准线于点由抛物线的定义,得到,再由平面几何知识可得当、、三点共线时,有最小值,因此算出到直线的距离,即可得到所求距离的最小值.
【解答】
解:双曲线:的渐近线方程为,
右顶点到其一条渐近线的距离等于,
可得,解得,
即有,
由题意可得,解得,
即有抛物线的方程为,设焦点为,
过点作于点,
作准线:于点,
连接,根据抛物线的定义得,
设到的距离为,到直线的距离为,
,
根据平面几何知识,可得当、、三点共线时,有最小值.
到直线:的距离为.
的最小值是,
由此可得所求距离和的最小值为.
故选B.
7.【答案】
【解析】
【分析】
本题考查抛物线的几何性质与标准方程,属于中档题.
设抛物线的准线为与轴的交点为,过点作,垂足为,连,因为且直线 的斜率为 ,于是可证明为正三角形,求出,进一步可知,,,从而得出抛物线的标准方程.
【解答】
解:设抛物线的准线为与轴的交点为,过点作,垂足为,连,
如图所示:
直线 的斜率为 ,,于是,
又根据已知条件以及抛物线的性质,知,
为正三角形,,,,
而由抛物线的性质知, ,
拋物线的方程为.
故选D.
8.【答案】
【解析】
【分析】
本题主要考查的是抛物线的标准方程与几何性质的应用,属于基础题.
可先求出抛物线的准线方程,再求值即可.
【解答】
解:由抛物线方程得,其准线方程为,
因为点到抛物线的准线的距离为,
所以,
解得或,
故选AB.
9.【答案】
【解析】
【分析】
本题考查抛物线性质,属于中档题.
解题时依据抛物线性质对每个选项逐一判断即可.
【解答】
解:选项A:抛物线为,其准线方程为,焦点,故A错;
选项B:设,在准线上投影为,
根据抛物线定义可知
,
所以线段中点到轴距离为,故B对;
选项C:设在准线上投影为,
,
,
当三点共线时取最值,
所以的周长的最小值为,故C对;
选项D:因为点,没有任何限制条件,可以是抛物线上任意两点,
所以以线段为直径的圆与准线不一定相切,故D错;
故选BC.
10.【答案】
【解析】
【分析】
由已知条件利用抛线的质得到,求出的值由此求出抛物线的标准方程.
本题考查抛物线的标准方程的求法,是基础题,解题时要掌握抛物线的性质.
【解答】
解:物线上一点到其准线的距离为,
,即,
抛物线的标准方程为.
故答案为.
11.【答案】
【解析】
【分析】
本题主要考查了抛物线的应用和抛物线的标准方程.解应用题需要把文字语言转化为形式化数学语言.介入一个抛物线方程,利用抛物线的性质来解决问题.
先建立适当坐标系,设抛物线方程为,把点代入抛物线方程,求得,得到抛物线方程,进行求解即可.
【解答】
解:建立如图所示的直角坐标系,
设抛物线方程为,
过定点,
将代入,得.
抛物线方程为.
设最长的支柱为,点的坐标为,解得,
点的坐标为,
.
故答案为:.
12.【答案】
【解析】
【分析】
本题考查圆的标准方程,抛物线的简单几何性质.
由题意,圆心的横坐标为,利用,可得点的纵坐标为,半径为,可得结论.
【解答】
解:由可得点的坐标为,准线的方程为,
由圆心在上,且圆与轴正半轴相切如图,
可得点的横坐标为,圆的半径为,,
又因为,
所以,所以,
所以点的纵坐标为,
所以圆的方程为.
故答案为.
13.【答案】
【解析】
【分析】
本题考查了抛物线的定义及其性质、平行线的性质、三角形面积计算公式,考查了推理能力与计算能力,属于难题.
求得的坐标由于轴,,,可得,,利用抛物线的定义可得,代入可得 ,再利用,即可得出.
【解答】
解:如图所示,.
轴,,,
,.
,解得,
代入可取,
,
解得.
故答案为.
14.【答案】或
【解析】
【分析】
本题考查抛物线的标准方程,抛物线的定义的应用,考查计算能力,属于中档题.
过做抛物线的准线的垂线,垂足为,则,当位于抛物线内,当,,共线时,的距离最小,,解得:,当位于抛物线外,由勾股定理可知:,或,当时,,则点在抛物线内,舍去,即可求得的值.
【解答】
解:由抛物线的定义可知:抛物线上的点到焦点距离等于该点到准线的距离,
过做抛物线的准线的垂线,垂足为,则,
当位于抛物线内,
,
当,,共线时,的距离最小,
由最小值为,即,解得:,
当位于抛物线外,
当,,共线时,取最小值,
即,解得:或,
由当时,,则点在抛物线内,舍去,
故答案为:或.
15.【答案】
【解析】
【分析】
本题考查了圆锥曲线的定义及其性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.
由于定点在定直线上,可得点的轨迹是不是抛物线;
利用双曲线的定义即可判断出正误;
对任意实数,由于原点到直线的距离,即可判断出正误;
利用椭圆的定义即可判断出正误;
方程的两根:,;即可判断出正误;
【解答】
解:由于定点在定直线上,可得到定点与定直线的距离相等的点的轨迹是直线,不是抛物线,不正确;
设,为两个定点,为常数且,若,只有当时,动点的轨迹是双曲线,因此不正确.
对任意实数,由于原点到直线的距离,因此对任意实数,直线总与定圆相切,正确.
在平面内,到两定点的距离的和等于常数的点的轨迹,只有当常数大于两定点的距离时才是椭圆,因此不正确;
方程的两根:,;可分别作为椭圆和双曲线的离心率,正确.
其中真命题的序号是.
故答案为:.
16.【答案】解:设双曲线的实轴长为,焦距为,虚轴长为,
则,
离心率,即,
又双曲线的虚轴长为,可得,
当双曲线焦点在轴时,所求双曲线的标准方程为;
当双曲线焦点在轴时,所求双曲线的标准方程为;
综上所述,所求双曲线的标准方程为或.
当抛物线的焦点在轴上时,可设所求抛物线的标准方程为,
将点的坐标代入抛物线的标准方程得,即,
此时,所求抛物线的标准方程为;
当抛物线的焦点在轴上时,可设所求抛物线的标准方程为,
将点的坐标代入抛物线的标准方程得,解得,
此时,所求抛物线的标准方程为,
综上所述,所求抛物线的标准方程为或.
【解析】本题考查双曲线的标准方程、双曲线的性质及几何意义、抛物线的标准方程,属于基础题.
根据题意求出,,然后分双曲线焦点在轴,轴上分别写出相应曲线的标准方程,即可求出结果;
分焦点在轴上和在轴上,设出抛物线方程,代入点的坐标,即可求出结果.
17.【答案】解:设抛物线型拱桥与水面两交点分别为,,
以垂直平分线为轴,拱圈最高点为坐标原点,建立平面直角坐标系,
则,,
设拱桥所在的抛物线方程为,
因点在抛物线上,代入解得,
故拱桥所在的抛物线方程是
船沿中线行驶,顶部最宽处的横坐标为,
因,故当时,,
故水位暴涨后,船身至少应降低米.
因精确到,故船身应降低.
答:船身应降低,才能安全通过桥洞.
【解析】本题考查抛物线的标准方程的运用,正确建立坐标系是关键,属于中档题.
设所在的抛物线方程为,待定系数法求方程;
当时,,船身至少应降低,进而得到答案.
18.【答案】解:直线的方程是,与联立,
从而有,
所以: ,
由抛物线定义得: ,
所以,
抛物线方程为 ;
由, .
化简得 ,
从而 ,
从而, ,,
设
,
且,即,
解得.
【解析】本题考查抛物线的标准方程及直线与抛物线的位置关系,属拔高题.
本小题考查抛物线的标准方程,直线的方程与联立,有,从而,再由抛物线定义得:,求得,则抛物线方程可得;
本小题考查圆锥曲线中的向量与参数问题,由,求得,再设的坐标,最后代入抛物线方程即可解得.
第1页,共1页
若抛物线上一点到焦点和到抛物线对称轴的距离分别为和,则抛物线的方程为( )
A. B.
C. 或 D. 或
已知抛物线的焦点为,为抛物线上一动点,,则的周长最小值为( )
A. B. C. D.
已知抛物线:上的点到的焦点的距离为,点在直线上的射影为,点关于轴的对称点为,则四边形的周长为( )
A. B. C. D.
已知抛物线:的焦点为,直线与抛物线交于,两点,若的中点的纵坐标为,则( )
A. B. C. D.
如图所示,点是抛物线的焦点,点,分别在抛物线及圆的实线部分上运动,且总是平行于轴,则的周长的取值范围是( )
A. B. C. D.
已知双曲线:的右顶点到其一条渐近线的距离等于,抛物线:的焦点与双曲线的右焦点重合,则抛物线上的动点到直线:和:的距离之和的最小值为( )
A. B. C. D.
已知拋物线的焦点为,点为拋物线上位于第一象限内一点,若且直线的斜率为,则拋物线的方程为( )
A. B. C. D.
点到抛物线的准线的距离为,则的值可以为( )
A. B. C. D.
已知抛物线的焦点为,是抛物线上两动点,是平面内一定点,下列说法正确的有( )
A. 准线方程为
B. 若,则线段中点到轴为
C. 的周长的最小值为
D. 以线段为直径的圆与准线相切
若抛物线上一点到其准线的距离为,则抛物线的标准方程为 .
某抛物线拱桥的跨度是米,中间拱高是米,在建桥时每隔米需用一支柱支撑,其中最长的支柱高是 米
设抛物线的焦点为,准线为,已知点在上,以为圆心的圆与轴的正半轴相切于点,若,则圆的方程为 .
在平面直角坐标系中,抛物线的焦点为,准线为,过抛物线上一点作的垂线,垂足为,与相交于点若,且的面积为,则的值为
点,抛物线的焦点为,若对于抛物线上的任意点,的最小值为,则的值等于 .
给出下列命题:
到定点与定直线的距离相等的点的轨迹是抛物线;
设为两个定点,为常数且,若,则动点的轨迹是双曲线。
对任意实数,直线总与某一个定圆相切。
在平面内,到两定点的距离的和等于常数的点的轨迹是椭圆;
方程的两根可分别作为椭圆和双曲线的离心率.
其中真命题的序号是 把你认为正确的命题的序号都填上。
求适合下列条件的曲线标准方程.
虚轴长为,离心率为的双曲线的标准方程;
过点的抛物线的标准方程.
河道上有一抛物线型拱桥,在正常水位时,拱圈最高点距水面,拱圈内水面宽,一条船在水面以上部分高,船顶部宽.
试建立适当的直角坐标系,求拱桥所在的抛物线的标准方程;
近日水位暴涨了,为此,必须加重船载,降低船身,才能通过桥洞,试问:船身至少应该降低多少 精确到
已知过抛物线的焦点,且斜率为的直线交抛物线于两点,且.
求该抛物线的方程;
为坐标原点,为抛物线上一点,若,求的值.
答案和解析
1.【答案】
【解析】
【分析】
由抛物线上点到抛物线对称轴的距离为,设该点为根据点坐标适合抛物线方程及点到焦点的距离为,列方程组,解之可得与的值,从而得到本题的答案.
本题已知抛物线上一点到焦点和到抛物线对称轴的距离,求抛物线的焦参数,着重考查了抛物线的标准方程与简单几何性质等知识,属于基础题.
【解答】
解:抛物线上一点到抛物线对称轴的距离为,
设该点为,则的坐标为
到抛物线的焦点的距离为
由抛物线的定义,得
点是抛物线上的点,
由联立,解得,或,
则抛物线方程为或.
故选:.
2.【答案】
【解析】
【分析】
本题考查抛物线的简单性质,考查数形结合思想,属于基础题.
由题意画出图形,过作准线的垂线,交抛物线于,则此时的周长最小,然后结合两点间的距离公式即可求解.
【解答】
解:如图,
抛物线:的焦点为,准线方程为.
过作准线的垂线,交抛物线于,则的周长最小.
最小值为.
故选:.
3.【答案】
【解析】
【分析】
本题考查抛物线的定义以及几何性质的应用,属于基础题.
根据题意可得四边形为直角梯形,结合抛物线的定义可得,再得出、,即可求四边形的周长.
【解答】
解:由抛物线的方程可知,,直线为抛物线的准线,
所以,四边形为直角梯形.
因为,所以根据抛物线的定义,得,
过点作轴于点,则,
在中,,
所以四边形的周长为,
故选B.
4.【答案】
【解析】
【分析】
本题主要考查了抛物线性质的应用,直线与抛物线的位置关系,属于基础题.
由抛物线的定义,得,根据中点的坐标公式,得,代入即可求解.
【解答】
解:由抛物线:可知,,得到,,
设,,因为的中点的纵坐标为,
所以,则.
故选C.
5.【答案】
【解析】
【分析】
本题考查抛物线的定义,考查抛物线与圆的位置关系,属于中档题.
由抛物线定义可得,从而的周长,确定点横坐标的范围,即可得到结论.
【解答】
解:抛物线的准线:,焦点,
由抛物线定义可得,
圆的圆心为,半径为,
的周长
,
由抛物线及圆可得交点的横坐标为,
,
,
故选B.
6.【答案】
【解析】
【分析】
本题考查双曲线的方程,主要是渐近线方程的运用,同时考查抛物线的方程,属于较难题.
求出双曲线的渐近线方程,运用点到直线的距离公式计算可得,进而得到,可得,进而得到抛物线的方程.连接,过点作于点,作准线于点由抛物线的定义,得到,再由平面几何知识可得当、、三点共线时,有最小值,因此算出到直线的距离,即可得到所求距离的最小值.
【解答】
解:双曲线:的渐近线方程为,
右顶点到其一条渐近线的距离等于,
可得,解得,
即有,
由题意可得,解得,
即有抛物线的方程为,设焦点为,
过点作于点,
作准线:于点,
连接,根据抛物线的定义得,
设到的距离为,到直线的距离为,
,
根据平面几何知识,可得当、、三点共线时,有最小值.
到直线:的距离为.
的最小值是,
由此可得所求距离和的最小值为.
故选B.
7.【答案】
【解析】
【分析】
本题考查抛物线的几何性质与标准方程,属于中档题.
设抛物线的准线为与轴的交点为,过点作,垂足为,连,因为且直线 的斜率为 ,于是可证明为正三角形,求出,进一步可知,,,从而得出抛物线的标准方程.
【解答】
解:设抛物线的准线为与轴的交点为,过点作,垂足为,连,
如图所示:
直线 的斜率为 ,,于是,
又根据已知条件以及抛物线的性质,知,
为正三角形,,,,
而由抛物线的性质知, ,
拋物线的方程为.
故选D.
8.【答案】
【解析】
【分析】
本题主要考查的是抛物线的标准方程与几何性质的应用,属于基础题.
可先求出抛物线的准线方程,再求值即可.
【解答】
解:由抛物线方程得,其准线方程为,
因为点到抛物线的准线的距离为,
所以,
解得或,
故选AB.
9.【答案】
【解析】
【分析】
本题考查抛物线性质,属于中档题.
解题时依据抛物线性质对每个选项逐一判断即可.
【解答】
解:选项A:抛物线为,其准线方程为,焦点,故A错;
选项B:设,在准线上投影为,
根据抛物线定义可知
,
所以线段中点到轴距离为,故B对;
选项C:设在准线上投影为,
,
,
当三点共线时取最值,
所以的周长的最小值为,故C对;
选项D:因为点,没有任何限制条件,可以是抛物线上任意两点,
所以以线段为直径的圆与准线不一定相切,故D错;
故选BC.
10.【答案】
【解析】
【分析】
由已知条件利用抛线的质得到,求出的值由此求出抛物线的标准方程.
本题考查抛物线的标准方程的求法,是基础题,解题时要掌握抛物线的性质.
【解答】
解:物线上一点到其准线的距离为,
,即,
抛物线的标准方程为.
故答案为.
11.【答案】
【解析】
【分析】
本题主要考查了抛物线的应用和抛物线的标准方程.解应用题需要把文字语言转化为形式化数学语言.介入一个抛物线方程,利用抛物线的性质来解决问题.
先建立适当坐标系,设抛物线方程为,把点代入抛物线方程,求得,得到抛物线方程,进行求解即可.
【解答】
解:建立如图所示的直角坐标系,
设抛物线方程为,
过定点,
将代入,得.
抛物线方程为.
设最长的支柱为,点的坐标为,解得,
点的坐标为,
.
故答案为:.
12.【答案】
【解析】
【分析】
本题考查圆的标准方程,抛物线的简单几何性质.
由题意,圆心的横坐标为,利用,可得点的纵坐标为,半径为,可得结论.
【解答】
解:由可得点的坐标为,准线的方程为,
由圆心在上,且圆与轴正半轴相切如图,
可得点的横坐标为,圆的半径为,,
又因为,
所以,所以,
所以点的纵坐标为,
所以圆的方程为.
故答案为.
13.【答案】
【解析】
【分析】
本题考查了抛物线的定义及其性质、平行线的性质、三角形面积计算公式,考查了推理能力与计算能力,属于难题.
求得的坐标由于轴,,,可得,,利用抛物线的定义可得,代入可得 ,再利用,即可得出.
【解答】
解:如图所示,.
轴,,,
,.
,解得,
代入可取,
,
解得.
故答案为.
14.【答案】或
【解析】
【分析】
本题考查抛物线的标准方程,抛物线的定义的应用,考查计算能力,属于中档题.
过做抛物线的准线的垂线,垂足为,则,当位于抛物线内,当,,共线时,的距离最小,,解得:,当位于抛物线外,由勾股定理可知:,或,当时,,则点在抛物线内,舍去,即可求得的值.
【解答】
解:由抛物线的定义可知:抛物线上的点到焦点距离等于该点到准线的距离,
过做抛物线的准线的垂线,垂足为,则,
当位于抛物线内,
,
当,,共线时,的距离最小,
由最小值为,即,解得:,
当位于抛物线外,
当,,共线时,取最小值,
即,解得:或,
由当时,,则点在抛物线内,舍去,
故答案为:或.
15.【答案】
【解析】
【分析】
本题考查了圆锥曲线的定义及其性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.
由于定点在定直线上,可得点的轨迹是不是抛物线;
利用双曲线的定义即可判断出正误;
对任意实数,由于原点到直线的距离,即可判断出正误;
利用椭圆的定义即可判断出正误;
方程的两根:,;即可判断出正误;
【解答】
解:由于定点在定直线上,可得到定点与定直线的距离相等的点的轨迹是直线,不是抛物线,不正确;
设,为两个定点,为常数且,若,只有当时,动点的轨迹是双曲线,因此不正确.
对任意实数,由于原点到直线的距离,因此对任意实数,直线总与定圆相切,正确.
在平面内,到两定点的距离的和等于常数的点的轨迹,只有当常数大于两定点的距离时才是椭圆,因此不正确;
方程的两根:,;可分别作为椭圆和双曲线的离心率,正确.
其中真命题的序号是.
故答案为:.
16.【答案】解:设双曲线的实轴长为,焦距为,虚轴长为,
则,
离心率,即,
又双曲线的虚轴长为,可得,
当双曲线焦点在轴时,所求双曲线的标准方程为;
当双曲线焦点在轴时,所求双曲线的标准方程为;
综上所述,所求双曲线的标准方程为或.
当抛物线的焦点在轴上时,可设所求抛物线的标准方程为,
将点的坐标代入抛物线的标准方程得,即,
此时,所求抛物线的标准方程为;
当抛物线的焦点在轴上时,可设所求抛物线的标准方程为,
将点的坐标代入抛物线的标准方程得,解得,
此时,所求抛物线的标准方程为,
综上所述,所求抛物线的标准方程为或.
【解析】本题考查双曲线的标准方程、双曲线的性质及几何意义、抛物线的标准方程,属于基础题.
根据题意求出,,然后分双曲线焦点在轴,轴上分别写出相应曲线的标准方程,即可求出结果;
分焦点在轴上和在轴上,设出抛物线方程,代入点的坐标,即可求出结果.
17.【答案】解:设抛物线型拱桥与水面两交点分别为,,
以垂直平分线为轴,拱圈最高点为坐标原点,建立平面直角坐标系,
则,,
设拱桥所在的抛物线方程为,
因点在抛物线上,代入解得,
故拱桥所在的抛物线方程是
船沿中线行驶,顶部最宽处的横坐标为,
因,故当时,,
故水位暴涨后,船身至少应降低米.
因精确到,故船身应降低.
答:船身应降低,才能安全通过桥洞.
【解析】本题考查抛物线的标准方程的运用,正确建立坐标系是关键,属于中档题.
设所在的抛物线方程为,待定系数法求方程;
当时,,船身至少应降低,进而得到答案.
18.【答案】解:直线的方程是,与联立,
从而有,
所以: ,
由抛物线定义得: ,
所以,
抛物线方程为 ;
由, .
化简得 ,
从而 ,
从而, ,,
设
,
且,即,
解得.
【解析】本题考查抛物线的标准方程及直线与抛物线的位置关系,属拔高题.
本小题考查抛物线的标准方程,直线的方程与联立,有,从而,再由抛物线定义得:,求得,则抛物线方程可得;
本小题考查圆锥曲线中的向量与参数问题,由,求得,再设的坐标,最后代入抛物线方程即可解得.
第1页,共1页
