数学人教A版(2019)必修第一册4.5.3函数模型的应用(共28张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.5.3函数模型的应用(共28张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 999.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 10:10:47 | ||
图片预览








文档简介
(共28张PPT)
4.5.3
函数模型的应用
高一数学必修第一册 第四章 指数函数和对数函数
1.理解函数是描述客观世界中变量关系和规律的重要数学语言和工具;
2.在实际情景中,会选择合适的函数类型刻画现实问题的变化规律;
3.收集、阅读一些现实生活、生产实际或者经济领域中的数学模型,体会人们是如何借助函数刻画实际问题的,感悟数学模型中参数的现实意义.
4.核心素养:数学建模、逻辑推理、数学运算.
学习目标
函数模型 函数解析式
一次函数模型
反比例函数模型
二次函数模型
指数型函数模型
对数型函数模型
幂函数型模型
几类常见函数模型
一、回顾旧知
二、函数模型的应用
人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律,可以为有效控制人口增长提供依据.早在1798年,英国经济学家马尔萨斯(T.R.Malthus,1766—1834)就提出了自然状态下的人口增长模型:y=y0ert,其中t表示经过的时间, y0表示t=0时的人口数,r表示人口的年平均增长率.
1.例3
根据国家统计局网站公布的数据,我国1950年末1959年末 的人口总数分别为55196万和67207万.根据这些数据,用马尔萨斯人口增长模型建立我国在1950~1959年期间的具体人口增长模型.
(1)
利用(1)中的模型计算1951~1958年各年年末的人口总数.查阅国家统计局网站公布的我国在1951~1958年间各年末的实际人口总数,并检验所得模型与实际人口数据是否相符.
年 份 1951 1952 1953 1954 1955 1956 1957 1958
计算人数/万 56417 57665 58940 60243 61576 62938 64330 65753
实际人数/万 56300 57482 58796 60266 61456 62828 64563 65994
(2)
以(1)中的模型作预测,大约在什么时候我国的人口总数达到13亿?
(3)
大约在1950年后的40年(即1990年)我国的人口就已达到13亿
2.例4.
解:
3.应用函数模型解决问题的基本过程
(1).审题:
弄清题意,分清条件和结论,理顺数量关系,
初步选择模型.
(2).建模:
将自然语言转化为数学语言,将文字语言转化
为符号语言,利用数学知识建立相应的数学模型.
(3).求模:
求解数学模型,得出数学模型.
(4).还原:
将数学结论还原为实际问题.
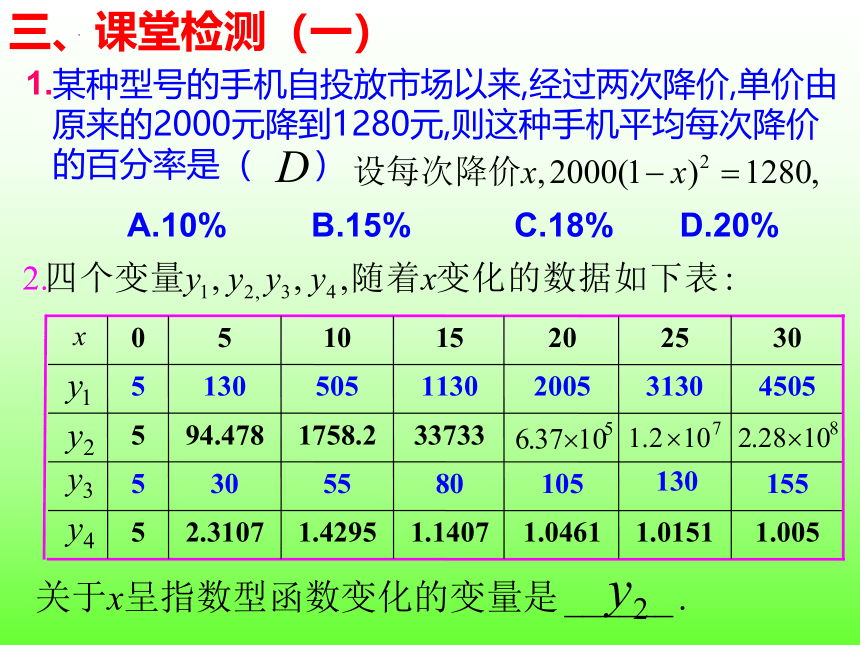
1.005
1.0151
1.0461
1.1407
1.4295
2.3107
5
155
130
105
80
55
30
5
33733
1758.2
94.478
5
4505
3130
2005
1130
505
130
5
30
25
20
15
10
5
0
某种型号的手机自投放市场以来,经过两次降价,单价由原来的2000元降到1280元,则这种手机平均每次降价的百分率是( )
A.10% B.15% C.18% D.20%
三、课堂检测(一)
1.
解:
3.例5.假如你有一笔资金用于投资,现有三种方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?
回报量
日回报量
累计回报量
选择投资方案
的标准
函数模型的应用
设第x天的日回报金额是y元
则方案一可以用函数_ ______________________ 描述
则方案二可以用函数_______________________ 描述;
则方案三可以用函数_ ______________________描述。
方案一
方案二
方案三
第1天
第3天
第2天
第4天
第5天
40
40
40
40
40
10
10×2
10×3
10×4
10×5
0.4
0.4×2
0.4×22
0.4×23
0.4×24
x/天 方案一 方案二 方案三
y/元 增长量/元 y/元 增长量/元 y/元 增长量/元
1 40 0 10 0.4
2 40 0 20 10 0.8 0.4
3 40 0 30 10 1.6 0.8
4 40 0 40 10 3.2 1.6
5 40 0 50 10 6.4 3.2
6 40 0 60 10 12.8 6.4
7 40 0 70 10 25.6 12.8
8 40 0 80 10 51.2 25.6
9 40 0 90 10 102.4 51.2
… … … … … … …
30 40 0 300 10 214748364.8 107374182.4
列表法比较三种方案的日回报量
投资__________ 应选择第一种投资方案;
投资___________应选择第一种或第二种投资方案;
投资___________应选择第二种投资方案;
投资____________________应选择第三种投资方案.
1~6天
7天
列表法比较三种方案的累计回报
8~10天
11天(含11天)以上
天数 方案 1 2 3 4 5 6 7 8 9 10 11
一 40 80 120 160 200 240 280 320 360 400 440
二 10 30 60 100 150 210 280 360 450 550 660
三 0.4 1.2 2.8 6 12.4 25.2 50.8 102 204.4 409.2 816.8
匀速增长
急剧增长
没有增长
三种函数模型的增长差异
下面利用图象从整体上把握不同函数模型的增长:
40
80
120
160
y
2
4
6
8
10
12
x
o
y=40
y= 10x
我们看到,底数为2的指数函数模型比线性函数模型增长速度要快得多.从中你对“指数爆炸”的含义有什么新的理解?
某公司2009年为了实现1000万元总利润的目标,他准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,但奖金数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:
y=0.25x,y=log7x+1,y=1.002x,
其中哪个模型能符合公司的要求呢?
1.函数变量x,y满足什么条件才算符合公司要求?
2.根据函数图象讨论哪个函数符合条件?
4.例6.
400
600
800
1000
200
1
2
3
4
5
6
7
8
x
y
o
y=0.25x
根据函数图象讨论哪个函数符合条件
观察图象发现:在[10,1000]上,模型y=0.25x,y=1.002x的图象有一部分在直线y=5上方,只有模型 的图象始终在y=5和y=0.25x下方,应选模型 奖金不超过25%.
400
600
800
1000
200
1
2
3
4
5
6
7
8
x
y
o
指数爆炸
y=0.25x
观察图象比较三种函数的增长情况
直线上升
对数平稳
1
2
3
4
5
6
7
8
y
400
600
800
1000
200
x
o
y=0.25x
-300
-250
-200
-150
-100
-50
y
400
600
800
1000
200
x
o
1200
用函数建立数学模型解决实际问题的基本过程
实际问题
实际问题的解
函数模型的解
推理
函数模型
解释说明
运算
化归
这一过程包括分析和理解实际问题的增长情况(是“对数增长”“直线上升”还是“指数爆炸”);根据增长情况选择函数类型构建数学模型,将实际问题化归为数学问题;通过运算、推理求解函数模型;用得到的函数模型描述实际问题的变化规律,解决有关问题.在这一过程中,往往需要利用信息技术帮助画图、运算等.
1.
酒驾是严重危害交通安全的违法行为,为了保障交通安全,根据国家有关规定:100mL血液中酒精含量低于20mg的驾驶员可以驾驶汽车,酒精含量达到20~79mg的驾驶员为酒后驾车,80mg及以上的认定为醉酒驾车, .假设某驾驶员一天晚上8点喝了一定量的酒后,其血液中的酒精含量上升到0.6 mg/mL,如果在停止喝酒后,他血液中酒精含量会以每小时10%的速度减少,则他次日上午最早几点开车才不构成酒后驾车?( )(精确到1h)(参考数据:lg3≈0.477)
解:设他至少要经过x小时才能驾驶汽车,
所以他至少要经过11小时才能驾驶汽车.(即早上7点)
A.6 B.7 C.8 D.9
四、课堂检测(二)
则0.6×(1-10%)x<20,所以3×0.9x<1,
某地方政府为鼓励全民创业,拟对本地产值在50万元到500万元的新增小微企业进行奖励,奖励方案遵循以下原则:奖金y(单位:万元)随年产值x(单位:万元)的增加而增加,且奖金不低于7万元,同时奖金不超过年产值的15%.
若某企业产值100万元,核定可得9万元奖金,试分析函数y=lg x+kx +5(k为常数)是否为符合政府要求的奖励函数模型,并说明原因(已知lg 2≈0.3,lg 5≈0.7)
2.
(1)
若采用函数 作为奖励函数模型,试确定最小的正整数a的值.
(2)
即奖金超过年产值的15%,不成立,故该函数模型不符合要求.
某地方政府为鼓励全民创业,拟对本地产值在50万元到500万元的新增小微企业进行奖励,奖励方案遵循以下原则:奖金y(单位:万元)随年产值x(单位:万元)的增加而增加,且奖金不低于7万元,同时奖金不超过年产值的15%.
2.
若采用函数 作为奖励函数模型,试确定最小的正整数a的值.
(2)
3.
医学上为研究传染病传播中病毒细胞的发展规律及其预防,将病毒细胞注入一只小白鼠的体内进行研究,经检测,将病毒细胞的增长数与天数的关系记录如下表.
天数 t 1 2 3 4 5 6
病毒细胞总数N 1 2 4 8 16 32
已知该种病毒细胞在小白鼠体内的个数超过 的时候,小白鼠将会死亡.如注射某种药物,可杀死其体内该病毒的98%.
(1)为了使小白鼠在试验过程中不死亡,第一次最迟应在何时注射
该种药物 (精确到天,已知
解:(1)题意知
即第一次最迟应在第27天注射该种药物.
(2)第二次最迟应在何时注射该种药物,才能维持小白鼠的生命
3.
医学上为研究传染病传播中病毒细胞的发展规律及其预防,将病毒细胞注入一只小白鼠的体内进行研究,经检测,将病毒细胞的增长数与天数的关系记录如下表.
天数 t 1 2 3 4 5 6
病毒细胞总数N 1 2 4 8 16 32
已知该种病毒细胞在小白鼠体内的个数超过 的时候,小白鼠将会死亡.如注射某种药物,可杀死其体内该病毒的98%.
(精确到天,已知
解:(2)由题意知,注射药物后小白鼠体内剩余的病毒细胞总数为
再经过 天后小白鼠体内病毒细胞总数为
即再经过6天必须注射药物,即第二次应在第33天注射药物.
1.本节你学习了哪些基本知识
五、课堂小结
作业: (1)课本P155 , 习题4.5 9、11、13题
(2)做完《一线课堂》对应习题
利用函数模型解决实际问题
2.用函数建立数学模型解决实际问题的基本过程
实际问题
实际问题的解
函数模型的解
推理
函数模型
解释说明
运算
化归
4.5.3
函数模型的应用
高一数学必修第一册 第四章 指数函数和对数函数
1.理解函数是描述客观世界中变量关系和规律的重要数学语言和工具;
2.在实际情景中,会选择合适的函数类型刻画现实问题的变化规律;
3.收集、阅读一些现实生活、生产实际或者经济领域中的数学模型,体会人们是如何借助函数刻画实际问题的,感悟数学模型中参数的现实意义.
4.核心素养:数学建模、逻辑推理、数学运算.
学习目标
函数模型 函数解析式
一次函数模型
反比例函数模型
二次函数模型
指数型函数模型
对数型函数模型
幂函数型模型
几类常见函数模型
一、回顾旧知
二、函数模型的应用
人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律,可以为有效控制人口增长提供依据.早在1798年,英国经济学家马尔萨斯(T.R.Malthus,1766—1834)就提出了自然状态下的人口增长模型:y=y0ert,其中t表示经过的时间, y0表示t=0时的人口数,r表示人口的年平均增长率.
1.例3
根据国家统计局网站公布的数据,我国1950年末1959年末 的人口总数分别为55196万和67207万.根据这些数据,用马尔萨斯人口增长模型建立我国在1950~1959年期间的具体人口增长模型.
(1)
利用(1)中的模型计算1951~1958年各年年末的人口总数.查阅国家统计局网站公布的我国在1951~1958年间各年末的实际人口总数,并检验所得模型与实际人口数据是否相符.
年 份 1951 1952 1953 1954 1955 1956 1957 1958
计算人数/万 56417 57665 58940 60243 61576 62938 64330 65753
实际人数/万 56300 57482 58796 60266 61456 62828 64563 65994
(2)
以(1)中的模型作预测,大约在什么时候我国的人口总数达到13亿?
(3)
大约在1950年后的40年(即1990年)我国的人口就已达到13亿
2.例4.
解:
3.应用函数模型解决问题的基本过程
(1).审题:
弄清题意,分清条件和结论,理顺数量关系,
初步选择模型.
(2).建模:
将自然语言转化为数学语言,将文字语言转化
为符号语言,利用数学知识建立相应的数学模型.
(3).求模:
求解数学模型,得出数学模型.
(4).还原:
将数学结论还原为实际问题.
1.005
1.0151
1.0461
1.1407
1.4295
2.3107
5
155
130
105
80
55
30
5
33733
1758.2
94.478
5
4505
3130
2005
1130
505
130
5
30
25
20
15
10
5
0
某种型号的手机自投放市场以来,经过两次降价,单价由原来的2000元降到1280元,则这种手机平均每次降价的百分率是( )
A.10% B.15% C.18% D.20%
三、课堂检测(一)
1.
解:
3.例5.假如你有一笔资金用于投资,现有三种方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?
回报量
日回报量
累计回报量
选择投资方案
的标准
函数模型的应用
设第x天的日回报金额是y元
则方案一可以用函数_ ______________________ 描述
则方案二可以用函数_______________________ 描述;
则方案三可以用函数_ ______________________描述。
方案一
方案二
方案三
第1天
第3天
第2天
第4天
第5天
40
40
40
40
40
10
10×2
10×3
10×4
10×5
0.4
0.4×2
0.4×22
0.4×23
0.4×24
x/天 方案一 方案二 方案三
y/元 增长量/元 y/元 增长量/元 y/元 增长量/元
1 40 0 10 0.4
2 40 0 20 10 0.8 0.4
3 40 0 30 10 1.6 0.8
4 40 0 40 10 3.2 1.6
5 40 0 50 10 6.4 3.2
6 40 0 60 10 12.8 6.4
7 40 0 70 10 25.6 12.8
8 40 0 80 10 51.2 25.6
9 40 0 90 10 102.4 51.2
… … … … … … …
30 40 0 300 10 214748364.8 107374182.4
列表法比较三种方案的日回报量
投资__________ 应选择第一种投资方案;
投资___________应选择第一种或第二种投资方案;
投资___________应选择第二种投资方案;
投资____________________应选择第三种投资方案.
1~6天
7天
列表法比较三种方案的累计回报
8~10天
11天(含11天)以上
天数 方案 1 2 3 4 5 6 7 8 9 10 11
一 40 80 120 160 200 240 280 320 360 400 440
二 10 30 60 100 150 210 280 360 450 550 660
三 0.4 1.2 2.8 6 12.4 25.2 50.8 102 204.4 409.2 816.8
匀速增长
急剧增长
没有增长
三种函数模型的增长差异
下面利用图象从整体上把握不同函数模型的增长:
40
80
120
160
y
2
4
6
8
10
12
x
o
y=40
y= 10x
我们看到,底数为2的指数函数模型比线性函数模型增长速度要快得多.从中你对“指数爆炸”的含义有什么新的理解?
某公司2009年为了实现1000万元总利润的目标,他准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,但奖金数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:
y=0.25x,y=log7x+1,y=1.002x,
其中哪个模型能符合公司的要求呢?
1.函数变量x,y满足什么条件才算符合公司要求?
2.根据函数图象讨论哪个函数符合条件?
4.例6.
400
600
800
1000
200
1
2
3
4
5
6
7
8
x
y
o
y=0.25x
根据函数图象讨论哪个函数符合条件
观察图象发现:在[10,1000]上,模型y=0.25x,y=1.002x的图象有一部分在直线y=5上方,只有模型 的图象始终在y=5和y=0.25x下方,应选模型 奖金不超过25%.
400
600
800
1000
200
1
2
3
4
5
6
7
8
x
y
o
指数爆炸
y=0.25x
观察图象比较三种函数的增长情况
直线上升
对数平稳
1
2
3
4
5
6
7
8
y
400
600
800
1000
200
x
o
y=0.25x
-300
-250
-200
-150
-100
-50
y
400
600
800
1000
200
x
o
1200
用函数建立数学模型解决实际问题的基本过程
实际问题
实际问题的解
函数模型的解
推理
函数模型
解释说明
运算
化归
这一过程包括分析和理解实际问题的增长情况(是“对数增长”“直线上升”还是“指数爆炸”);根据增长情况选择函数类型构建数学模型,将实际问题化归为数学问题;通过运算、推理求解函数模型;用得到的函数模型描述实际问题的变化规律,解决有关问题.在这一过程中,往往需要利用信息技术帮助画图、运算等.
1.
酒驾是严重危害交通安全的违法行为,为了保障交通安全,根据国家有关规定:100mL血液中酒精含量低于20mg的驾驶员可以驾驶汽车,酒精含量达到20~79mg的驾驶员为酒后驾车,80mg及以上的认定为醉酒驾车, .假设某驾驶员一天晚上8点喝了一定量的酒后,其血液中的酒精含量上升到0.6 mg/mL,如果在停止喝酒后,他血液中酒精含量会以每小时10%的速度减少,则他次日上午最早几点开车才不构成酒后驾车?( )(精确到1h)(参考数据:lg3≈0.477)
解:设他至少要经过x小时才能驾驶汽车,
所以他至少要经过11小时才能驾驶汽车.(即早上7点)
A.6 B.7 C.8 D.9
四、课堂检测(二)
则0.6×(1-10%)x<20,所以3×0.9x<1,
某地方政府为鼓励全民创业,拟对本地产值在50万元到500万元的新增小微企业进行奖励,奖励方案遵循以下原则:奖金y(单位:万元)随年产值x(单位:万元)的增加而增加,且奖金不低于7万元,同时奖金不超过年产值的15%.
若某企业产值100万元,核定可得9万元奖金,试分析函数y=lg x+kx +5(k为常数)是否为符合政府要求的奖励函数模型,并说明原因(已知lg 2≈0.3,lg 5≈0.7)
2.
(1)
若采用函数 作为奖励函数模型,试确定最小的正整数a的值.
(2)
即奖金超过年产值的15%,不成立,故该函数模型不符合要求.
某地方政府为鼓励全民创业,拟对本地产值在50万元到500万元的新增小微企业进行奖励,奖励方案遵循以下原则:奖金y(单位:万元)随年产值x(单位:万元)的增加而增加,且奖金不低于7万元,同时奖金不超过年产值的15%.
2.
若采用函数 作为奖励函数模型,试确定最小的正整数a的值.
(2)
3.
医学上为研究传染病传播中病毒细胞的发展规律及其预防,将病毒细胞注入一只小白鼠的体内进行研究,经检测,将病毒细胞的增长数与天数的关系记录如下表.
天数 t 1 2 3 4 5 6
病毒细胞总数N 1 2 4 8 16 32
已知该种病毒细胞在小白鼠体内的个数超过 的时候,小白鼠将会死亡.如注射某种药物,可杀死其体内该病毒的98%.
(1)为了使小白鼠在试验过程中不死亡,第一次最迟应在何时注射
该种药物 (精确到天,已知
解:(1)题意知
即第一次最迟应在第27天注射该种药物.
(2)第二次最迟应在何时注射该种药物,才能维持小白鼠的生命
3.
医学上为研究传染病传播中病毒细胞的发展规律及其预防,将病毒细胞注入一只小白鼠的体内进行研究,经检测,将病毒细胞的增长数与天数的关系记录如下表.
天数 t 1 2 3 4 5 6
病毒细胞总数N 1 2 4 8 16 32
已知该种病毒细胞在小白鼠体内的个数超过 的时候,小白鼠将会死亡.如注射某种药物,可杀死其体内该病毒的98%.
(精确到天,已知
解:(2)由题意知,注射药物后小白鼠体内剩余的病毒细胞总数为
再经过 天后小白鼠体内病毒细胞总数为
即再经过6天必须注射药物,即第二次应在第33天注射药物.
1.本节你学习了哪些基本知识
五、课堂小结
作业: (1)课本P155 , 习题4.5 9、11、13题
(2)做完《一线课堂》对应习题
利用函数模型解决实际问题
2.用函数建立数学模型解决实际问题的基本过程
实际问题
实际问题的解
函数模型的解
推理
函数模型
解释说明
运算
化归
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
