第6章 数据与分析 单元复习(课件)(共38张PPT)
文档属性
| 名称 | 第6章 数据与分析 单元复习(课件)(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 19:15:23 | ||
图片预览





文档简介
(共38张PPT)
第6章数据与分析单元复习
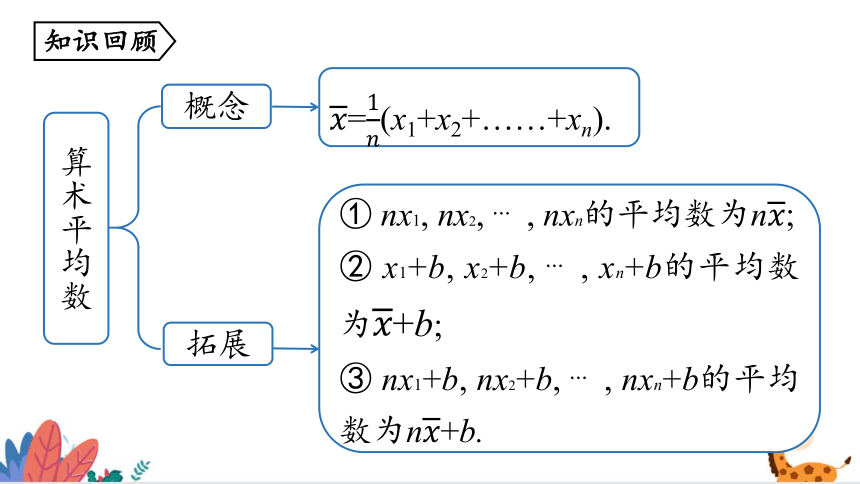
算术平均数
概念
拓展
=(x1+x2+……+xn).
① nx1, nx2, , nxn的平均数为n;
② x1+b, x2+b, , xn+b的平均数为+b;
③ nx1+b, nx2+b, , nxn+b的平均数为n+b.
知识回顾
平均数的性质
若一组数据 x1,x2, xn的平均数为,则有:
(1)数据nx1,nx2, nxn的平均数为n;
(2)数据x1+b,x2+b, xn+b的平均数为+b;
(3)数据nx1+b,nx2+b, nxn+b的平均数为n+b.
知识回顾
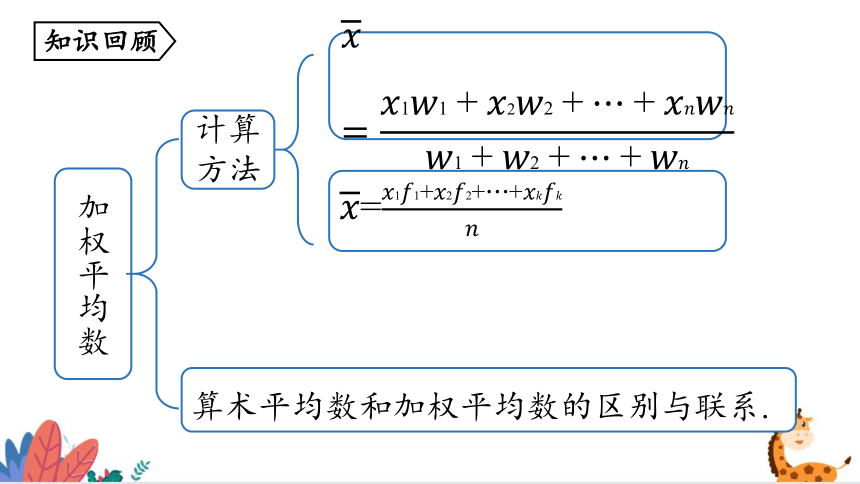
加权平均数
计算
方法
算术平均数和加权平均数的区别与联系.
=
知识回顾
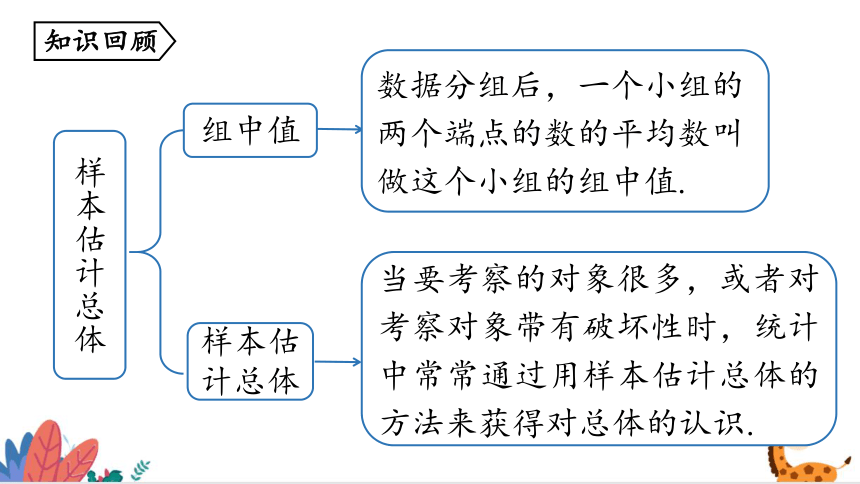
样本估计总体
组中值
样本估计总体
数据分组后,一个小组的两个端点的数的平均数叫做这个小组的组中值.
当要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.
知识回顾
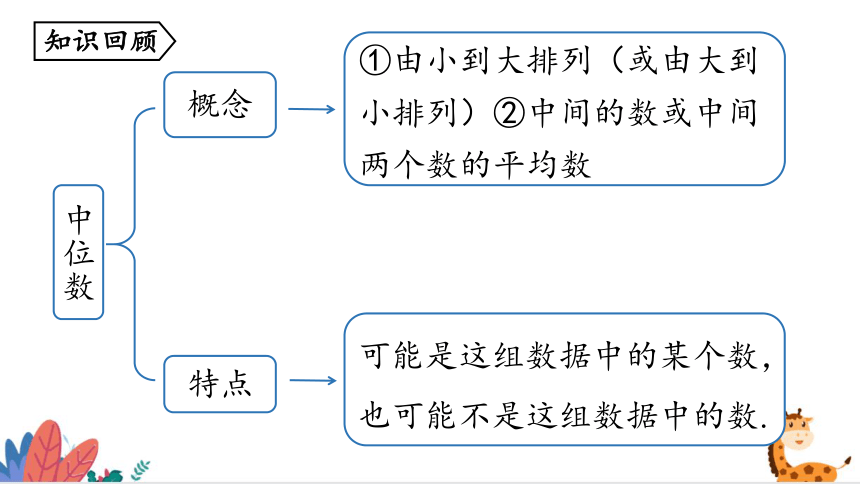
中位数
概念
特点
①由小到大排列(或由大到小排列)②中间的数或中间两个数的平均数
可能是这组数据中的某个数,也可能不是这组数据中的数.
知识回顾
众数
概念
注意
一组数据中出现次数最多的数据称为这组数据的众数.
众数是一组数据中出现次数最多的数据,而不是数据出现的次数.
知识回顾
方差
概念
意义
….
方差越大,数据的波动越大;方差越小,数据的波动越小.
知识回顾
作用
步骤
比较数据的稳定性.
先计算样本数据的平均数,然后计算样本方差,再利用样本方差来估计总体数据的波动情况.
用样本方差估计总体方差
知识回顾
1. 算术平均数
一般地,如果有 n 个数 x1,x2, ,xn,那么我们把(x1+x2+ +xn)叫做这 n 个数的算术平均数,简称平均数,记作 ,读作 x拔,则有 =(x1+x2+ +xn).
2. 加权平均数
一般地,如果有 n 个数 x1,x2, ,xn 的权分别为 w1,w2, ,wn,那么我们把叫做这n个数的加权平均数.
在求 n 个数的平均数时,如果 x1 出现 f1 次, x2 出现 f2 次, , xk 出现 fk 次(这里的 f1+ f2+ +fk =n),那么这 n 个数的平均数 = .也叫做 x1,x2, ,xk 这 k 个数的加权平均数,其中 f1, f2, , fk分别叫做 x1,x2, ,xk 的权.
4. 中位数
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
5. 众数
一组数据中出现次数最多的数据称为这组数据的众数.
注意:众数是一组数据中出现次数最多的数据,而不是数据出现的次数.
6. 方差
设有 n 个数据 x1,x2, ,xn,各数据与它们的平均数 的差的平方分别是,,
我们用这些值的平均数,即用+
来衡量这组数据波动的大小,并把它叫做这组数据的方差,记作 .
7. 方差的意义
方差可以反映数据的波动程度,即:
方差越大,数据的波动越大;
方差越小,数据的波动越小.
8. 用样本方差估计总体方差
用样本估计总体是统计的基本思想,类似于用样本的平均数估计总体的平均数,考察总体方差的时候,如果考察的总体包含很多个体,或者考察本身带有破坏性,实际中常常会用样本的方差来估计总体的方差.
1.某公司 33 名职工的月工资(以元为单位)如下:
(1)求该公司职工月工资的平均数、中位数、众数.(精确到个位)
职工 董事长 副董 事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 5500 5000 3500 3000 2500 2000 1500
(3)你认为哪个统计量更能反映这个公司职工的月工资水平?结合问题谈一谈你的看法.
(2)假设副董事长的工资从 5000 元提升到 20000 元,董事长的工资从 5500 元提升到 30000 元,那么新的平均数、中位数、众数又是什么?(精确到个位)
解析:(1)平均数
(元)
把这 33 个数据按照从小到大的顺序可得中位数为 1500.
这 33 个数据中出现次数最多的数据是 1500,出现了 20 次,所以众数为 1500.
(2)新的平均数
(元)
把这 33 个数据按照从小到大的顺序可得新的中位数仍为 1500.
这 33 个数据中出现次数最多的数据是 1500,出现了20 次,所以新的众数仍为 1500.
(3)中位数或众数都能反映出这个公司职工的月工资水平.
由于董事长、副董事长的工资偏高,使月平均工资与绝大多数职工的月工资差距很大,也就是说用平均数来反映这个公司职工的月工资水平有很大误差.
选择合适的统计量表示一组数据集中趋势的方法
当一组数据中某些数据重复出现时,众数往往作为首选的统计量;当个别数据偏差较大时,常用中位数反映该组数据的集中趋势.选择的统计量要能代表这组数据全部或绝大部分的特征.
2.某中学数学活动小组为了调查居民的用水情况,从某社区的 1500 户家庭中随机抽取了 30 户家庭的月用水量,结果如下表所示:
月用水量/吨 3 4 5 7 8 9 10
户数 4 3 5 11 4 2 1
解:平均数为(吨),众数是7吨,中位数是7吨.
(1)求这 30 户家庭月用水量的平均数、众数和中位数;
月用水量/吨 3 4 5 7 8 9 10
户数 4 3 5 11 4 2 1
由题意可知15006.2=9300(吨),所以该社区月用水量约为9300吨.
(2)根据上述数据,试估计该社区的月用水量;
(3)由于我国水资源缺乏,许多城市常利用分段计费的方法引导市民节约用水,即规定每个家庭的月基本用水量为m(吨),家庭月用水量不超过m(吨)的部分按原价收费,超过m(吨)的部分加倍收费,你认为上述问题中的平均数、众数和中位数哪个作为基本用水量比较合适?
(3)以中位数或者众数作为月基本用水量较为合理.
理由:因为这样既可以满足大多数家庭用水量,也可以引导用水量高于7吨的家庭节约用水.
3.甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
某同学计算出了甲的成绩平均数是9,方差是[++]=0.8,请作答:
(1)在图中用折线统计图将甲运动员的成绩表示出来;
(2)若甲、乙射击成绩平均数都一样,则a+b= .
解析:a+b=95-10-9-9=17.
17
解:a=7,b=10或 a=10,b=7.理由如下:
∵甲的成绩比乙的成绩稳定,所以乙的方差>0.8.
∴[++]>0.8 .
即(a - 9)2+(b - 9)2 >3.
∵a+b=17,且a,b均小于或等于10.
(3)在(2)的条件下,当甲比乙的成绩较稳定时,请列举出a,b的所有可能取值,并说明理由.
∴当a=7,b=10时, (a - 9)2+(b - 9)2 >3 ,符合题意.
当a=8,b=9时, (a - 9)2+(b - 9)2 <3,不符合题意.
当a=9,b=8时, (a - 9)2+(b - 9)2 <3,不符合题意.
当a=10,b=7时, (a - 9)2+(b - 9)2>3,符合题意.
∴a=7,b=10或 a=10,b=7.
4.某班拟派一名跳远运动员参加学校运动会,对甲、乙两名跳远运动员进行了 8 次测试,他们的成绩(单位:m)如下:
甲:3.68,3.65,3.68,3.69,3.74,3.73,3.68,3.67
乙:3.60,3.73,3.72,3.61,3.62,3.71,3.79,3.75
经预测,跳 3.70m 方可获得冠军,你认为应该派谁去?
解:∵ 8 次测试中,甲有 2 次成绩超过 3.70m,而乙有 5 次成绩超过 3.70m,∴应该派乙运动员去参加比赛.
易错警示:事实上,要派谁去就要看谁的成绩更容易达到或超过3.70m.本题易错误地通过方差的大小来确定甲应该去,没有结合实际情况进行分析.
5.如图是某市连续 5 天的天气情况.
解:(1)5天中日最高气温的平均数为
5天中日最低气温的平均数为
(1)利用方差判断该城市这5天的日最高气温波动大还是日最低气温波动大?
5天中日最高气温的方差
5天中日最低气温的方差
所以该市5天的日最低气温的波动较大.
解:25日、26日、27日的天气现象依次是大雨、中雨、晴,空气质量依次是良、优、优,说明了下雨后空气质量改善了.
25日、26日、27日、28日、29日的日温差依次是2℃、3℃、8℃、10℃、7℃,可以看出雨天的日温差较小.
(2)根据图中提供的信息,请再写出两个不同类型的结论.
第6章数据与分析单元复习
算术平均数
概念
拓展
=(x1+x2+……+xn).
① nx1, nx2, , nxn的平均数为n;
② x1+b, x2+b, , xn+b的平均数为+b;
③ nx1+b, nx2+b, , nxn+b的平均数为n+b.
知识回顾
平均数的性质
若一组数据 x1,x2, xn的平均数为,则有:
(1)数据nx1,nx2, nxn的平均数为n;
(2)数据x1+b,x2+b, xn+b的平均数为+b;
(3)数据nx1+b,nx2+b, nxn+b的平均数为n+b.
知识回顾
加权平均数
计算
方法
算术平均数和加权平均数的区别与联系.
=
知识回顾
样本估计总体
组中值
样本估计总体
数据分组后,一个小组的两个端点的数的平均数叫做这个小组的组中值.
当要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.
知识回顾
中位数
概念
特点
①由小到大排列(或由大到小排列)②中间的数或中间两个数的平均数
可能是这组数据中的某个数,也可能不是这组数据中的数.
知识回顾
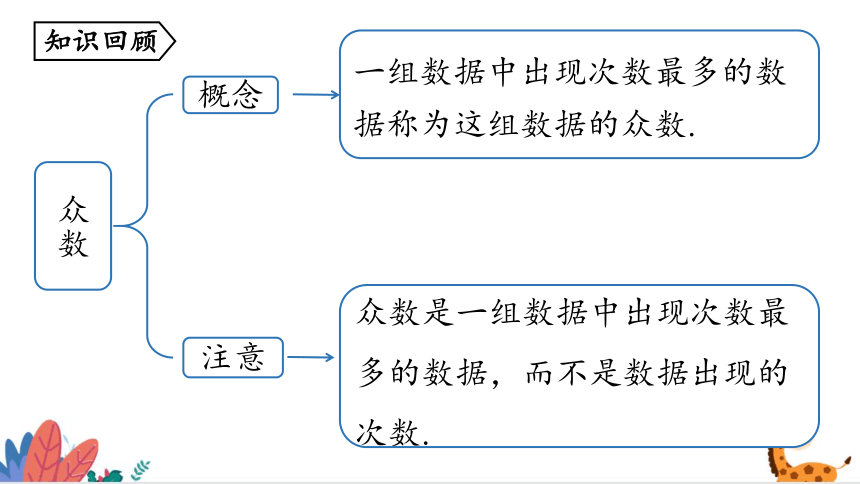
众数
概念
注意
一组数据中出现次数最多的数据称为这组数据的众数.
众数是一组数据中出现次数最多的数据,而不是数据出现的次数.
知识回顾
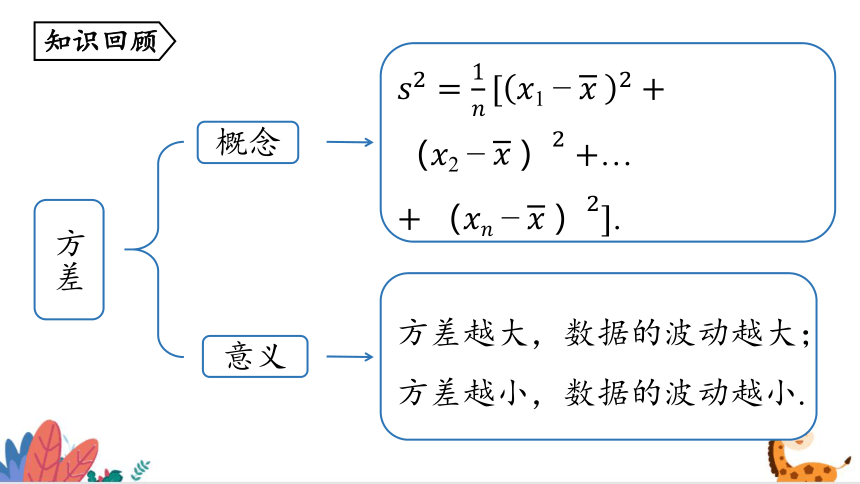
方差
概念
意义
….
方差越大,数据的波动越大;方差越小,数据的波动越小.
知识回顾
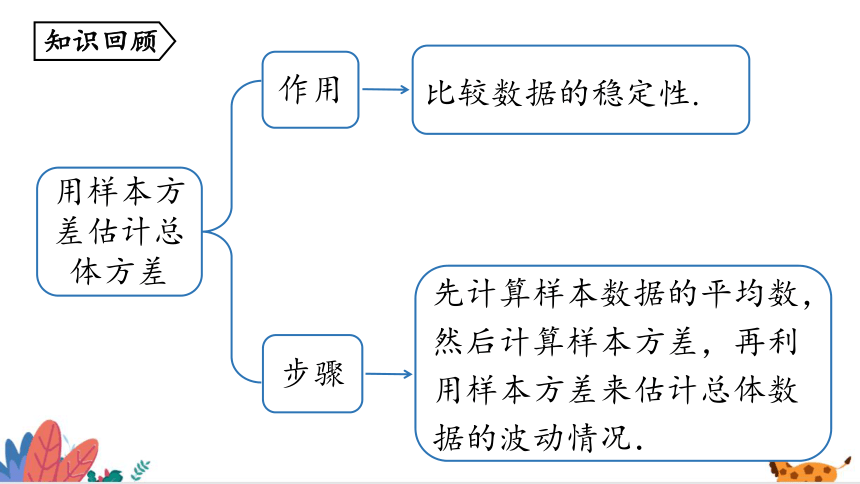
作用
步骤
比较数据的稳定性.
先计算样本数据的平均数,然后计算样本方差,再利用样本方差来估计总体数据的波动情况.
用样本方差估计总体方差
知识回顾
1. 算术平均数
一般地,如果有 n 个数 x1,x2, ,xn,那么我们把(x1+x2+ +xn)叫做这 n 个数的算术平均数,简称平均数,记作 ,读作 x拔,则有 =(x1+x2+ +xn).
2. 加权平均数
一般地,如果有 n 个数 x1,x2, ,xn 的权分别为 w1,w2, ,wn,那么我们把叫做这n个数的加权平均数.
在求 n 个数的平均数时,如果 x1 出现 f1 次, x2 出现 f2 次, , xk 出现 fk 次(这里的 f1+ f2+ +fk =n),那么这 n 个数的平均数 = .也叫做 x1,x2, ,xk 这 k 个数的加权平均数,其中 f1, f2, , fk分别叫做 x1,x2, ,xk 的权.
4. 中位数
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
5. 众数
一组数据中出现次数最多的数据称为这组数据的众数.
注意:众数是一组数据中出现次数最多的数据,而不是数据出现的次数.
6. 方差
设有 n 个数据 x1,x2, ,xn,各数据与它们的平均数 的差的平方分别是,,
我们用这些值的平均数,即用+
来衡量这组数据波动的大小,并把它叫做这组数据的方差,记作 .
7. 方差的意义
方差可以反映数据的波动程度,即:
方差越大,数据的波动越大;
方差越小,数据的波动越小.
8. 用样本方差估计总体方差
用样本估计总体是统计的基本思想,类似于用样本的平均数估计总体的平均数,考察总体方差的时候,如果考察的总体包含很多个体,或者考察本身带有破坏性,实际中常常会用样本的方差来估计总体的方差.
1.某公司 33 名职工的月工资(以元为单位)如下:
(1)求该公司职工月工资的平均数、中位数、众数.(精确到个位)
职工 董事长 副董 事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 5500 5000 3500 3000 2500 2000 1500
(3)你认为哪个统计量更能反映这个公司职工的月工资水平?结合问题谈一谈你的看法.
(2)假设副董事长的工资从 5000 元提升到 20000 元,董事长的工资从 5500 元提升到 30000 元,那么新的平均数、中位数、众数又是什么?(精确到个位)
解析:(1)平均数
(元)
把这 33 个数据按照从小到大的顺序可得中位数为 1500.
这 33 个数据中出现次数最多的数据是 1500,出现了 20 次,所以众数为 1500.
(2)新的平均数
(元)
把这 33 个数据按照从小到大的顺序可得新的中位数仍为 1500.
这 33 个数据中出现次数最多的数据是 1500,出现了20 次,所以新的众数仍为 1500.
(3)中位数或众数都能反映出这个公司职工的月工资水平.
由于董事长、副董事长的工资偏高,使月平均工资与绝大多数职工的月工资差距很大,也就是说用平均数来反映这个公司职工的月工资水平有很大误差.
选择合适的统计量表示一组数据集中趋势的方法
当一组数据中某些数据重复出现时,众数往往作为首选的统计量;当个别数据偏差较大时,常用中位数反映该组数据的集中趋势.选择的统计量要能代表这组数据全部或绝大部分的特征.
2.某中学数学活动小组为了调查居民的用水情况,从某社区的 1500 户家庭中随机抽取了 30 户家庭的月用水量,结果如下表所示:
月用水量/吨 3 4 5 7 8 9 10
户数 4 3 5 11 4 2 1
解:平均数为(吨),众数是7吨,中位数是7吨.
(1)求这 30 户家庭月用水量的平均数、众数和中位数;
月用水量/吨 3 4 5 7 8 9 10
户数 4 3 5 11 4 2 1
由题意可知15006.2=9300(吨),所以该社区月用水量约为9300吨.
(2)根据上述数据,试估计该社区的月用水量;
(3)由于我国水资源缺乏,许多城市常利用分段计费的方法引导市民节约用水,即规定每个家庭的月基本用水量为m(吨),家庭月用水量不超过m(吨)的部分按原价收费,超过m(吨)的部分加倍收费,你认为上述问题中的平均数、众数和中位数哪个作为基本用水量比较合适?
(3)以中位数或者众数作为月基本用水量较为合理.
理由:因为这样既可以满足大多数家庭用水量,也可以引导用水量高于7吨的家庭节约用水.
3.甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
某同学计算出了甲的成绩平均数是9,方差是[++]=0.8,请作答:
(1)在图中用折线统计图将甲运动员的成绩表示出来;
(2)若甲、乙射击成绩平均数都一样,则a+b= .
解析:a+b=95-10-9-9=17.
17
解:a=7,b=10或 a=10,b=7.理由如下:
∵甲的成绩比乙的成绩稳定,所以乙的方差>0.8.
∴[++]>0.8 .
即(a - 9)2+(b - 9)2 >3.
∵a+b=17,且a,b均小于或等于10.
(3)在(2)的条件下,当甲比乙的成绩较稳定时,请列举出a,b的所有可能取值,并说明理由.
∴当a=7,b=10时, (a - 9)2+(b - 9)2 >3 ,符合题意.
当a=8,b=9时, (a - 9)2+(b - 9)2 <3,不符合题意.
当a=9,b=8时, (a - 9)2+(b - 9)2 <3,不符合题意.
当a=10,b=7时, (a - 9)2+(b - 9)2>3,符合题意.
∴a=7,b=10或 a=10,b=7.
4.某班拟派一名跳远运动员参加学校运动会,对甲、乙两名跳远运动员进行了 8 次测试,他们的成绩(单位:m)如下:
甲:3.68,3.65,3.68,3.69,3.74,3.73,3.68,3.67
乙:3.60,3.73,3.72,3.61,3.62,3.71,3.79,3.75
经预测,跳 3.70m 方可获得冠军,你认为应该派谁去?
解:∵ 8 次测试中,甲有 2 次成绩超过 3.70m,而乙有 5 次成绩超过 3.70m,∴应该派乙运动员去参加比赛.
易错警示:事实上,要派谁去就要看谁的成绩更容易达到或超过3.70m.本题易错误地通过方差的大小来确定甲应该去,没有结合实际情况进行分析.
5.如图是某市连续 5 天的天气情况.
解:(1)5天中日最高气温的平均数为
5天中日最低气温的平均数为
(1)利用方差判断该城市这5天的日最高气温波动大还是日最低气温波动大?
5天中日最高气温的方差
5天中日最低气温的方差
所以该市5天的日最低气温的波动较大.
解:25日、26日、27日的天气现象依次是大雨、中雨、晴,空气质量依次是良、优、优,说明了下雨后空气质量改善了.
25日、26日、27日、28日、29日的日温差依次是2℃、3℃、8℃、10℃、7℃,可以看出雨天的日温差较小.
(2)根据图中提供的信息,请再写出两个不同类型的结论.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
