2022-2023学年人教版七年级数学上册4.3.2 角的比较运算 课件 (共16张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学上册4.3.2 角的比较运算 课件 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 08:15:14 | ||
图片预览



文档简介
(共16张PPT)
4.3.2角的比较运算
学习目标:
(1)能说出角平分线的定义及角的数量关系,会用图形语言、符号语言进行描述.
(2)类比线段的中点学分线,体会类比思想.
学习重点:
结合图形理解角平分线的意义,并会用符号语言进行描述.
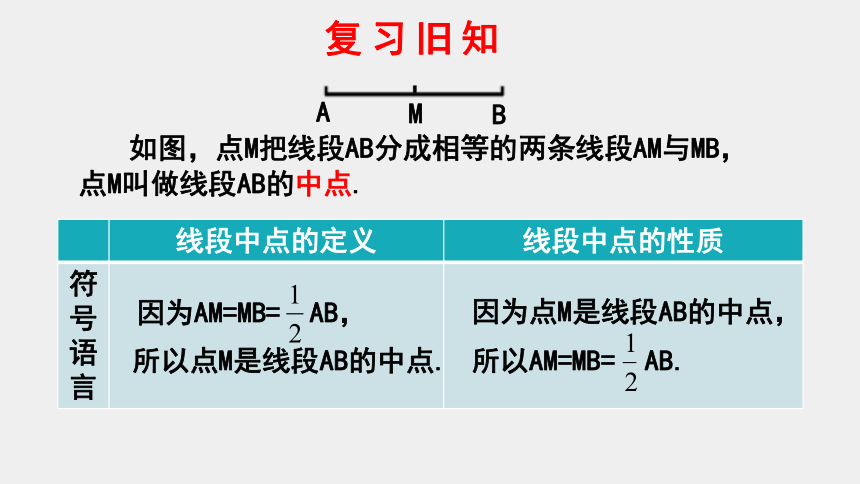
如图,点M把线段AB分成相等的两条线段AM与MB,点M叫做线段AB的中点.
A
B
M
线段中点的定义 线段中点的性质
符号语言
因为AM=MB= AB,
所以点M是线段AB的中点.
因为点M是线段AB的中点,
所以AM=MB= AB.
复习旧知
引入新课
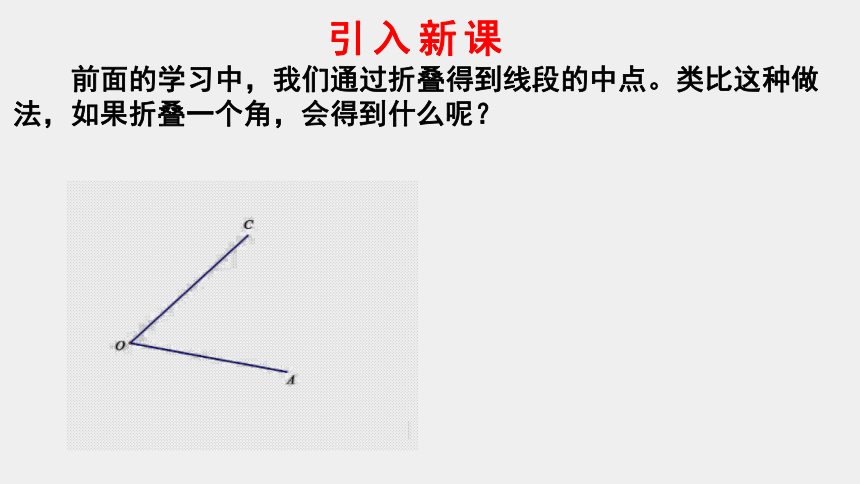
前面的学习中,我们通过折叠得到线段的中点。类比这种做法,如果折叠一个角,会得到什么呢?
引入新课
前面的学习中,我们通过折叠得到线段的中点。类比这种做法,如果折叠一个角,会得到什么呢?
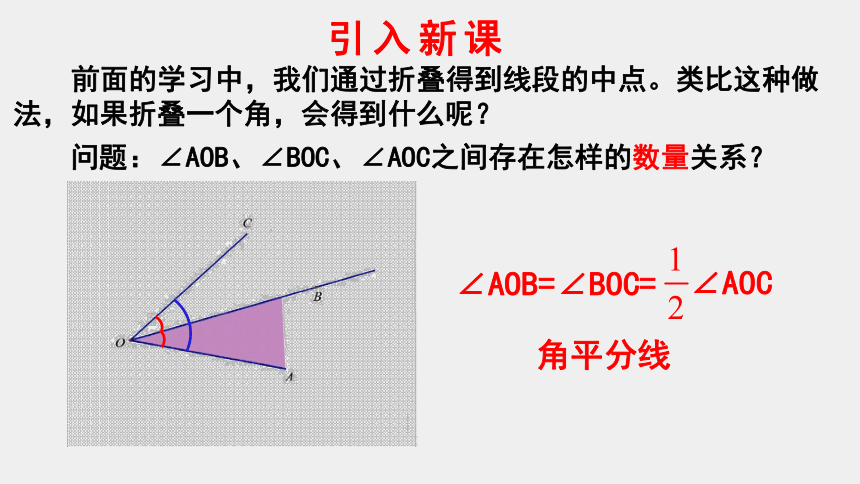
问题:∠AOB、∠BOC、∠AOC之间存在怎样的数量关系?
∠AOB=∠BOC=
角平分线
∠AOC
角平分线的定义 角平分线的性质
符号语言
因为∠AOB=
所以射线OB是∠AOC的平分线.
因为射线OB是∠AOC的平分线,
所以∠AOB=∠BOC= ∠AOC.
得出概念
从一个角的顶点出发,把这个角分成两个
相等的角的射线,叫做这个角的平分线.
B
∠BOC
= ∠AOC,
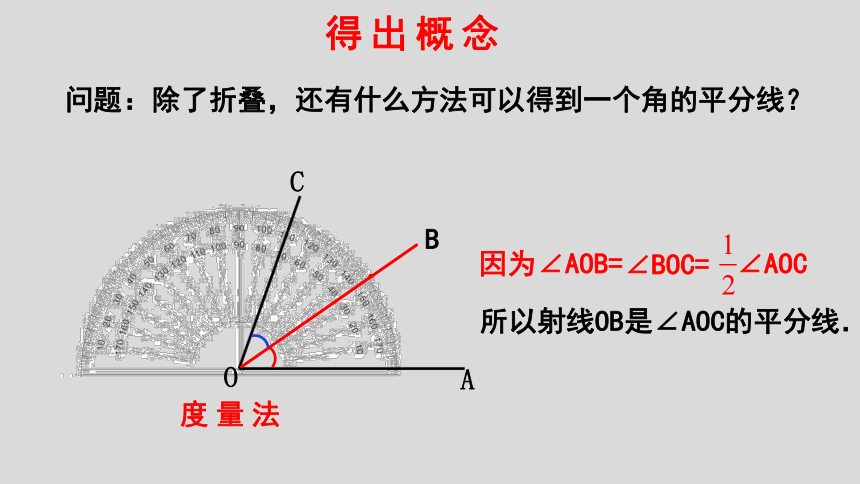
问题:除了折叠,还有什么方法可以得到一个角的平分线?
得出概念
O
C
A
B
因为∠AOB=
所以射线OB是∠AOC的平分线.
度量法
∠BOC=
∠AOC
35°
35°
练习1:
⑴如图,射线OC为∠AOB的平分线,∠AOC=35°,则∠BOC= ,∠AOB= .
课堂练习
35°
70°
⑵如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是( ) .
A.20° B.40°
C.70° D.80°
D
C
B
1
2
A
O
课堂练习
C
∠2= ∠BOC= ×140°=70°
∠BOC=
180°
?
∠AOB-∠1=180°-40°= 140°
= ∠AOD ,
得出概念
类似的,还有角的三等分线.
所以射线OB、OC是∠AOD的三等分线.
符号语言:
因为∠AOB
一个角有2条三等分线
同理可以得到角的四等分线、五等分线…… n等分线.
3条
4条
(n-1)条
=∠BOC
=∠COD
例1.把一个周角7等分,每一份是多少度的角(精确到分)?
例题讲解
分析:1个周角为360°,把它7等分,每份角的度数可由360°÷7计算得出.
答:每份是51°26′的角.
有余数,可以把度的余数化成分后再除.
51°+3°÷7
≈ 51°26′
解:360°÷7 =
= 51°+180′÷7
≈ 51°+
除不尽,25.714……′
26′
O
B
C
A
E
D
例2.如图,OB是∠AOC的平分线,OD是∠COE的平分线,∠AOB=40°,∠COE=60°,求∠BOD的度数.
例题讲解
60°
40°
2
1
所以∠2= ∠COE
所以∠BOD=∠1+∠2= 40°+30°=70°.
解:因为OB是∠AOC的平分线,
所以∠1=∠AOB=40°.
因为OD是∠COE的平分线,
∠BOD=
-∠AOB
-∠DOE
∠AOE
= ×60°=30°,
加法
减法
练习2.如图,OB是∠AOC的平分线,OD是∠COE的平分线,∠AOE=140°,∠COD=30°,求∠AOB的度数?
O
B
C
A
E
D
课堂练习
解:因为OD是∠COE的平分线,∠COD=30°,
所以∠COE=2∠COD=60°,
所以∠AOC=∠AOE-∠COE
=140°-60°= 80°.
又因为OB是∠AOC的平分线,
所以∠AOB= ∠AOC= ×80°=40°.
60°
30°
∠AOC=
40°
?
=140°-60°
减法
∠AOE
-
∠COE
=80°
140°
角平分线的定义 角平分线的性质
符号语言
因为∠AOB=
所以射线OB是∠AOC的平分线.
因为射线OB是∠AOC的平分线,
所以∠AOB=∠BOC= ∠AOC.
课堂小结
B
∠BOC
= ∠AOC,
从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
1、角的平分线:
因为∠AOB=∠BOC=∠COD= ∠AOD,
2.角的三等分线:
符号语言:
课堂小结
3.同理可以得到角的四等分线、五等分线…… n等分线.
所以射线OB、OC是∠AOD的三等分线.
谢 谢 观 看!
4.3.2角的比较运算
学习目标:
(1)能说出角平分线的定义及角的数量关系,会用图形语言、符号语言进行描述.
(2)类比线段的中点学分线,体会类比思想.
学习重点:
结合图形理解角平分线的意义,并会用符号语言进行描述.
如图,点M把线段AB分成相等的两条线段AM与MB,点M叫做线段AB的中点.
A
B
M
线段中点的定义 线段中点的性质
符号语言
因为AM=MB= AB,
所以点M是线段AB的中点.
因为点M是线段AB的中点,
所以AM=MB= AB.
复习旧知
引入新课
前面的学习中,我们通过折叠得到线段的中点。类比这种做法,如果折叠一个角,会得到什么呢?
引入新课
前面的学习中,我们通过折叠得到线段的中点。类比这种做法,如果折叠一个角,会得到什么呢?
问题:∠AOB、∠BOC、∠AOC之间存在怎样的数量关系?
∠AOB=∠BOC=
角平分线
∠AOC
角平分线的定义 角平分线的性质
符号语言
因为∠AOB=
所以射线OB是∠AOC的平分线.
因为射线OB是∠AOC的平分线,
所以∠AOB=∠BOC= ∠AOC.
得出概念
从一个角的顶点出发,把这个角分成两个
相等的角的射线,叫做这个角的平分线.
B
∠BOC
= ∠AOC,
问题:除了折叠,还有什么方法可以得到一个角的平分线?
得出概念
O
C
A
B
因为∠AOB=
所以射线OB是∠AOC的平分线.
度量法
∠BOC=
∠AOC
35°
35°
练习1:
⑴如图,射线OC为∠AOB的平分线,∠AOC=35°,则∠BOC= ,∠AOB= .
课堂练习
35°
70°
⑵如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是( ) .
A.20° B.40°
C.70° D.80°
D
C
B
1
2
A
O
课堂练习
C
∠2= ∠BOC= ×140°=70°
∠BOC=
180°
?
∠AOB-∠1=180°-40°= 140°
= ∠AOD ,
得出概念
类似的,还有角的三等分线.
所以射线OB、OC是∠AOD的三等分线.
符号语言:
因为∠AOB
一个角有2条三等分线
同理可以得到角的四等分线、五等分线…… n等分线.
3条
4条
(n-1)条
=∠BOC
=∠COD
例1.把一个周角7等分,每一份是多少度的角(精确到分)?
例题讲解
分析:1个周角为360°,把它7等分,每份角的度数可由360°÷7计算得出.
答:每份是51°26′的角.
有余数,可以把度的余数化成分后再除.
51°+3°÷7
≈ 51°26′
解:360°÷7 =
= 51°+180′÷7
≈ 51°+
除不尽,25.714……′
26′
O
B
C
A
E
D
例2.如图,OB是∠AOC的平分线,OD是∠COE的平分线,∠AOB=40°,∠COE=60°,求∠BOD的度数.
例题讲解
60°
40°
2
1
所以∠2= ∠COE
所以∠BOD=∠1+∠2= 40°+30°=70°.
解:因为OB是∠AOC的平分线,
所以∠1=∠AOB=40°.
因为OD是∠COE的平分线,
∠BOD=
-∠AOB
-∠DOE
∠AOE
= ×60°=30°,
加法
减法
练习2.如图,OB是∠AOC的平分线,OD是∠COE的平分线,∠AOE=140°,∠COD=30°,求∠AOB的度数?
O
B
C
A
E
D
课堂练习
解:因为OD是∠COE的平分线,∠COD=30°,
所以∠COE=2∠COD=60°,
所以∠AOC=∠AOE-∠COE
=140°-60°= 80°.
又因为OB是∠AOC的平分线,
所以∠AOB= ∠AOC= ×80°=40°.
60°
30°
∠AOC=
40°
?
=140°-60°
减法
∠AOE
-
∠COE
=80°
140°
角平分线的定义 角平分线的性质
符号语言
因为∠AOB=
所以射线OB是∠AOC的平分线.
因为射线OB是∠AOC的平分线,
所以∠AOB=∠BOC= ∠AOC.
课堂小结
B
∠BOC
= ∠AOC,
从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
1、角的平分线:
因为∠AOB=∠BOC=∠COD= ∠AOD,
2.角的三等分线:
符号语言:
课堂小结
3.同理可以得到角的四等分线、五等分线…… n等分线.
所以射线OB、OC是∠AOD的三等分线.
谢 谢 观 看!
