5.1任意角和弧度制 练习(含答案)
文档属性
| 名称 | 5.1任意角和弧度制 练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 00:00:00 | ||
图片预览

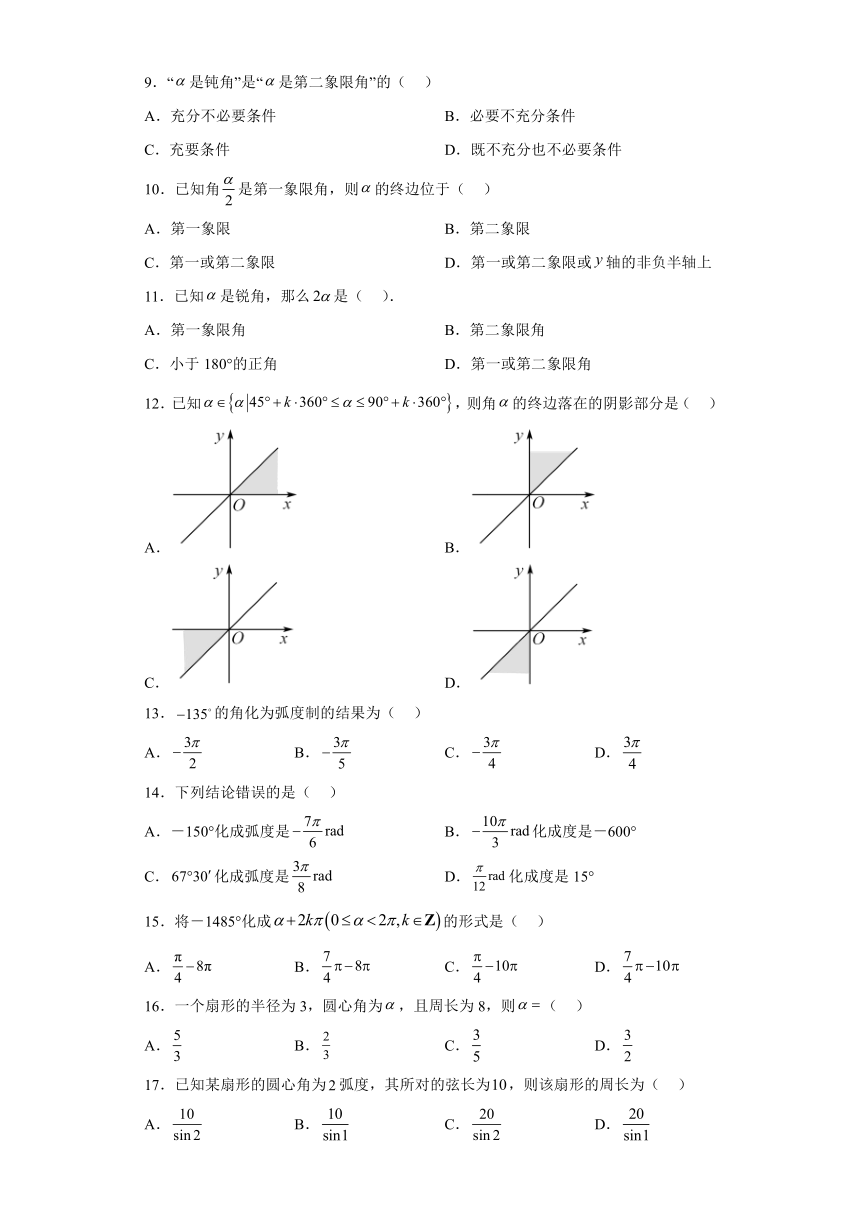


文档简介
任意角和弧度制
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.喜洋洋从家步行到学校,一般需要10分钟,则10分钟时间钟表的分针走过的角度是( )
A.30° B.﹣30° C.60° D.﹣60°
2.如图,圆的圆周上一点以为起点按逆时针方向旋转,转一圈,之后从起始位置转过的角是( )
A. B. C. D.
3.与终边相同的角是( )
A. B. C. D.
4.将轴正半轴绕原点逆时针旋转,得到角,则下列与终边相同的角是( )
A. B. C. D.
5.终边落在直线上的角的集合为( )
A. B.
C. D.
6.若,,则角与角的终边一定( )
A.重合 B.关于原点对称
C.关于x轴对称 D.关于y轴对称
7.如果角与角x+45°具有相同的终边,角与角x-45°具有相同的终边,那么与之间的关系是( )
A. B.
C. D.
8.若,则的终边在( )
A.第二或第三象限 B.第一或第三象限
C.第二或第四象限 D.第三或第四象限
9.“是钝角”是“是第二象限角”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
10.已知角是第一象限角,则的终边位于( )
A.第一象限 B.第二象限
C.第一或第二象限 D.第一或第二象限或轴的非负半轴上
11.已知是锐角,那么是( ).
A.第一象限角 B.第二象限角
C.小于180°的正角 D.第一或第二象限角
12.已知,则角的终边落在的阴影部分是( )
A. B.
C. D.
13.的角化为弧度制的结果为( )
A. B. C. D.
14.下列结论错误的是( )
A.-150°化成弧度是 B.化成度是-600°
C.化成弧度是 D.化成度是15°
15.将-1485°化成的形式是( )
A. B. C. D.
16.一个扇形的半径为3,圆心角为,且周长为8,则( )
A. B. C. D.
17.已知某扇形的圆心角为弧度,其所对的弦长为,则该扇形的周长为( )
A. B. C. D.
18.半径为2cm,圆心角为1rad的扇形的面积为( )
A. B. C. D.
19.折扇又名“撒扇”“纸扇”,是一种用竹木或象牙做扇骨、韧纸或绫绢做扇面的能折叠的扇子,如图1.其平面图如图2的扇形AOB,其中,,则扇面(曲边四边形ABDC)的面积是( )
A. B. C. D.
20.玉雕在我国历史悠久,拥有深厚的文化底蕴,数千年来始终以其独特的内涵与魅力深深吸引着世人.某扇形玉雕壁画尺寸(单位:cm)如图所示,则该玉雕壁画的扇面面积约为( )
A. B. C. D.
21.扇形的弧长为12,面积为24,则圆心角的弧度数为( )
A.4 B.3 C.2 D.1
22.已知弧长为的弧所对的圆心角为,则该弧所在的扇形面积为( )
A. B. C. D.
23.已知扇形的圆心角为,面积为8,则该扇形的周长为( )
A.12 B.10 C. D.
24.已知某扇形的面积为3,则该扇形的周长最小值为( )
A.2 B.4 C. D.
25.《掷铁饼者》取材于希腊的现实生活中的体育竞技活动,刻画的是一名强健的男子在掷铁饼过程中具有表现力的瞬间(如图).现在把掷铁饼者张开的双臂近似看成一张拉满弦的“弓”,掷铁饼者的手臂长约为,肩宽约为,“弓”所在圆的半径约为,则掷铁饼者双手之间的距离约为(参考数据:,)( )
A.1.012m B.1.768m C.2.043m D.2.945m
26.《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积(弦×矢+矢2),弧田(如图)由圆弧和其所对弦围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,按照上述经验公式计算所得弧田面积与其实际面积之间存在误差,现有圆心角为,弧长等于的弧田,按照上述经验公式计算所得弧田面积约是(参考数据)( )
A. B. C. D.
二、双空题
27.如图,花样滑冰是冰上运动项目之一.运动员通过冰刀在冰面上划出图形,并表演跳跃、旋转等高难度动作.运动员在原地转身的动作中,仅仅几秒内就能旋转十几圈,甚至二十几圈,因此,花样滑冰美丽而危险.运动员顺时针旋转两圈半所得角的度数是______,逆时针旋转两圈半所得角的度数是______.
28.已知扇形AOB的周长为8,在这个扇形的面积取得最大值时,其对应的圆心角的大小为___________,弦长AB为___________.
三、填空题
29.自行车大链轮有36齿,小链轮有24齿,当大链轮转过一周时,小链轮转过的角度是_____________度.
30.与终边相同的最小正角是____.
31.的角化为角度制的结果为_______.
32.已知世界上倾斜度最高的摩天大厦坐落于阿联酋的阿布扎比,其倾斜度达到18°,请用弧度表示倾斜度______.
33.用弧度制写出终边落在直线上的角是__.
34.如图,用弧度制表示终边落在阴影部分(包括边界)的角的集合:______.
35.用弧度制表示终边落在如图所示阴影部分内(含边界)的角的集合是__________.
36.已知一扇形的弧所对的圆心角为,半径,则扇形的弧长为___________.
37.已知扇形的圆心角为120°,扇形的弧长为,则该扇形所在圆的半径为___________.
38.东方设计中的“白银比例”是,它的重要程度不亚于西方文化中的“黄金比例”,传达出一种独特的东方审美观.折扇的纸面可看作是从一个大扇形纸面中剪掉一个小扇形纸面后剩下的图形(如图).设制作折扇时剪下的小扇形纸面面积为,折扇纸面面积为,当时,扇面看上去较为美观,那么剪下的小扇形半径与原大扇形半径之比的平方为________.
四、解答题
39.求下列各式的值,并作图说明运算的几何意义.
(1);
(2);
(3).
40.在内找出与下列各角终边相同的角,并指出它们是第几象限角:
(1)3290°;
(2);
(3);
(4).
41.求与角终边相同的最小正角和最大负角,并指出角是第几象限角.
42.已知角的终边落在图中阴影部分(不包括边界),试表示角的取值集合.
43.如图,,分别是终边落在射线OA,OB位置上的两个角,且,.
(1)求终边落在阴影部分(不包括边界)的角的集合;
(2)求终边落在阴影部分(不包括边界),且在内的角的集合.
44.写出终边在图中阴影区域(包括边界)内的角的集合.
45.写出与下列各角终边相同的角的集合,并指出内与它终边相同的角.
(1);
(2);
(3);
(4).
46.如果一个扇形的周长为,那么当它的半径和圆心角分别为多少时,扇形的面积最大?
47.某企业欲做一个介绍企业发展史的铭牌,铭牌的截面形状是如图所示的扇形环面(由扇形OAD挖去扇形OBC后构成的).已知,,线段BA,CD与,的长度之和为30,圆心角为弧度.
(1)求关于x的函数表达式;
(2)记铭牌的截面面积为y,试问x取何值时,y的值最大?并求出最大值.
参考答案:
1.D2.D3.D4.B5.B6.C7.D8.B9.A10.D11.C12.B13.C14.A15.D16.B17.D 18.D19.C20.D21.B22.B23.A24.D25.B26.B
27. 900° 28. 2 29.–540°##
30.° 31. 32.
33. 34.
35. 36.##
37.3 38.##
39.(1)30°
(2)-120°
(3)210°
40.(1)角与3290°角终边相同,它是第一象限角;
(2)与角终边相同,它是第二象限角;
(3)与角终边相同,它是第二象限角;
(4)与角终边相同,它是第二象限角;
41.最小正角为,最大负角为,角是第四象限角
42.或
43.(1).
(2).
44.(1);
(2);
(3).
45.(1),,;
(2),,;
(3),,;
(4),,.
46.当扇形的半径为,圆心角为时,扇形的面积最大
47.(1);
(2),.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.喜洋洋从家步行到学校,一般需要10分钟,则10分钟时间钟表的分针走过的角度是( )
A.30° B.﹣30° C.60° D.﹣60°
2.如图,圆的圆周上一点以为起点按逆时针方向旋转,转一圈,之后从起始位置转过的角是( )
A. B. C. D.
3.与终边相同的角是( )
A. B. C. D.
4.将轴正半轴绕原点逆时针旋转,得到角,则下列与终边相同的角是( )
A. B. C. D.
5.终边落在直线上的角的集合为( )
A. B.
C. D.
6.若,,则角与角的终边一定( )
A.重合 B.关于原点对称
C.关于x轴对称 D.关于y轴对称
7.如果角与角x+45°具有相同的终边,角与角x-45°具有相同的终边,那么与之间的关系是( )
A. B.
C. D.
8.若,则的终边在( )
A.第二或第三象限 B.第一或第三象限
C.第二或第四象限 D.第三或第四象限
9.“是钝角”是“是第二象限角”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
10.已知角是第一象限角,则的终边位于( )
A.第一象限 B.第二象限
C.第一或第二象限 D.第一或第二象限或轴的非负半轴上
11.已知是锐角,那么是( ).
A.第一象限角 B.第二象限角
C.小于180°的正角 D.第一或第二象限角
12.已知,则角的终边落在的阴影部分是( )
A. B.
C. D.
13.的角化为弧度制的结果为( )
A. B. C. D.
14.下列结论错误的是( )
A.-150°化成弧度是 B.化成度是-600°
C.化成弧度是 D.化成度是15°
15.将-1485°化成的形式是( )
A. B. C. D.
16.一个扇形的半径为3,圆心角为,且周长为8,则( )
A. B. C. D.
17.已知某扇形的圆心角为弧度,其所对的弦长为,则该扇形的周长为( )
A. B. C. D.
18.半径为2cm,圆心角为1rad的扇形的面积为( )
A. B. C. D.
19.折扇又名“撒扇”“纸扇”,是一种用竹木或象牙做扇骨、韧纸或绫绢做扇面的能折叠的扇子,如图1.其平面图如图2的扇形AOB,其中,,则扇面(曲边四边形ABDC)的面积是( )
A. B. C. D.
20.玉雕在我国历史悠久,拥有深厚的文化底蕴,数千年来始终以其独特的内涵与魅力深深吸引着世人.某扇形玉雕壁画尺寸(单位:cm)如图所示,则该玉雕壁画的扇面面积约为( )
A. B. C. D.
21.扇形的弧长为12,面积为24,则圆心角的弧度数为( )
A.4 B.3 C.2 D.1
22.已知弧长为的弧所对的圆心角为,则该弧所在的扇形面积为( )
A. B. C. D.
23.已知扇形的圆心角为,面积为8,则该扇形的周长为( )
A.12 B.10 C. D.
24.已知某扇形的面积为3,则该扇形的周长最小值为( )
A.2 B.4 C. D.
25.《掷铁饼者》取材于希腊的现实生活中的体育竞技活动,刻画的是一名强健的男子在掷铁饼过程中具有表现力的瞬间(如图).现在把掷铁饼者张开的双臂近似看成一张拉满弦的“弓”,掷铁饼者的手臂长约为,肩宽约为,“弓”所在圆的半径约为,则掷铁饼者双手之间的距离约为(参考数据:,)( )
A.1.012m B.1.768m C.2.043m D.2.945m
26.《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积(弦×矢+矢2),弧田(如图)由圆弧和其所对弦围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,按照上述经验公式计算所得弧田面积与其实际面积之间存在误差,现有圆心角为,弧长等于的弧田,按照上述经验公式计算所得弧田面积约是(参考数据)( )
A. B. C. D.
二、双空题
27.如图,花样滑冰是冰上运动项目之一.运动员通过冰刀在冰面上划出图形,并表演跳跃、旋转等高难度动作.运动员在原地转身的动作中,仅仅几秒内就能旋转十几圈,甚至二十几圈,因此,花样滑冰美丽而危险.运动员顺时针旋转两圈半所得角的度数是______,逆时针旋转两圈半所得角的度数是______.
28.已知扇形AOB的周长为8,在这个扇形的面积取得最大值时,其对应的圆心角的大小为___________,弦长AB为___________.
三、填空题
29.自行车大链轮有36齿,小链轮有24齿,当大链轮转过一周时,小链轮转过的角度是_____________度.
30.与终边相同的最小正角是____.
31.的角化为角度制的结果为_______.
32.已知世界上倾斜度最高的摩天大厦坐落于阿联酋的阿布扎比,其倾斜度达到18°,请用弧度表示倾斜度______.
33.用弧度制写出终边落在直线上的角是__.
34.如图,用弧度制表示终边落在阴影部分(包括边界)的角的集合:______.
35.用弧度制表示终边落在如图所示阴影部分内(含边界)的角的集合是__________.
36.已知一扇形的弧所对的圆心角为,半径,则扇形的弧长为___________.
37.已知扇形的圆心角为120°,扇形的弧长为,则该扇形所在圆的半径为___________.
38.东方设计中的“白银比例”是,它的重要程度不亚于西方文化中的“黄金比例”,传达出一种独特的东方审美观.折扇的纸面可看作是从一个大扇形纸面中剪掉一个小扇形纸面后剩下的图形(如图).设制作折扇时剪下的小扇形纸面面积为,折扇纸面面积为,当时,扇面看上去较为美观,那么剪下的小扇形半径与原大扇形半径之比的平方为________.
四、解答题
39.求下列各式的值,并作图说明运算的几何意义.
(1);
(2);
(3).
40.在内找出与下列各角终边相同的角,并指出它们是第几象限角:
(1)3290°;
(2);
(3);
(4).
41.求与角终边相同的最小正角和最大负角,并指出角是第几象限角.
42.已知角的终边落在图中阴影部分(不包括边界),试表示角的取值集合.
43.如图,,分别是终边落在射线OA,OB位置上的两个角,且,.
(1)求终边落在阴影部分(不包括边界)的角的集合;
(2)求终边落在阴影部分(不包括边界),且在内的角的集合.
44.写出终边在图中阴影区域(包括边界)内的角的集合.
45.写出与下列各角终边相同的角的集合,并指出内与它终边相同的角.
(1);
(2);
(3);
(4).
46.如果一个扇形的周长为,那么当它的半径和圆心角分别为多少时,扇形的面积最大?
47.某企业欲做一个介绍企业发展史的铭牌,铭牌的截面形状是如图所示的扇形环面(由扇形OAD挖去扇形OBC后构成的).已知,,线段BA,CD与,的长度之和为30,圆心角为弧度.
(1)求关于x的函数表达式;
(2)记铭牌的截面面积为y,试问x取何值时,y的值最大?并求出最大值.
参考答案:
1.D2.D3.D4.B5.B6.C7.D8.B9.A10.D11.C12.B13.C14.A15.D16.B17.D 18.D19.C20.D21.B22.B23.A24.D25.B26.B
27. 900° 28. 2 29.–540°##
30.° 31. 32.
33. 34.
35. 36.##
37.3 38.##
39.(1)30°
(2)-120°
(3)210°
40.(1)角与3290°角终边相同,它是第一象限角;
(2)与角终边相同,它是第二象限角;
(3)与角终边相同,它是第二象限角;
(4)与角终边相同,它是第二象限角;
41.最小正角为,最大负角为,角是第四象限角
42.或
43.(1).
(2).
44.(1);
(2);
(3).
45.(1),,;
(2),,;
(3),,;
(4),,.
46.当扇形的半径为,圆心角为时,扇形的面积最大
47.(1);
(2),.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
