15.2.3 整数指数幂(2)课件(共25张PPT)
文档属性
| 名称 | 15.2.3 整数指数幂(2)课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 00:00:00 | ||
图片预览



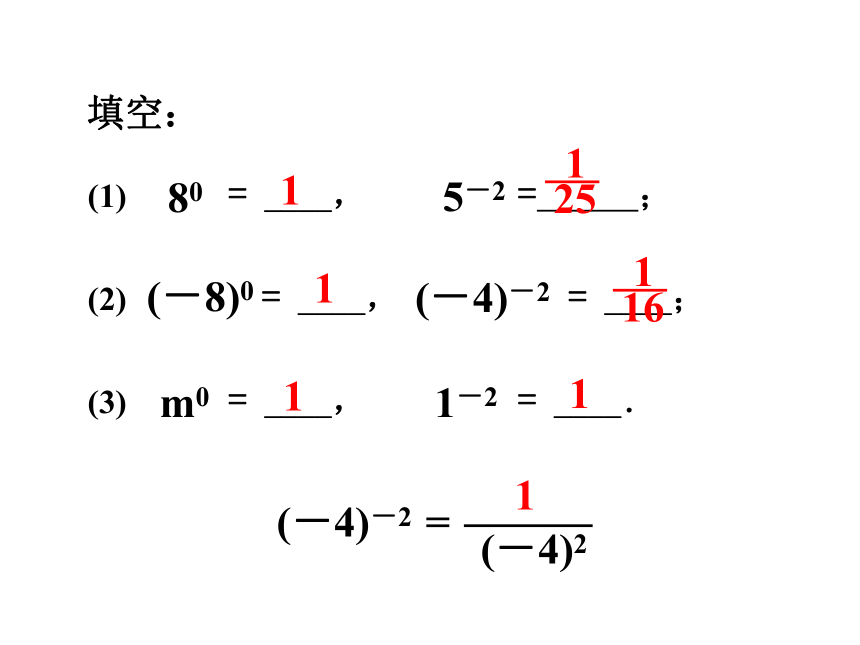
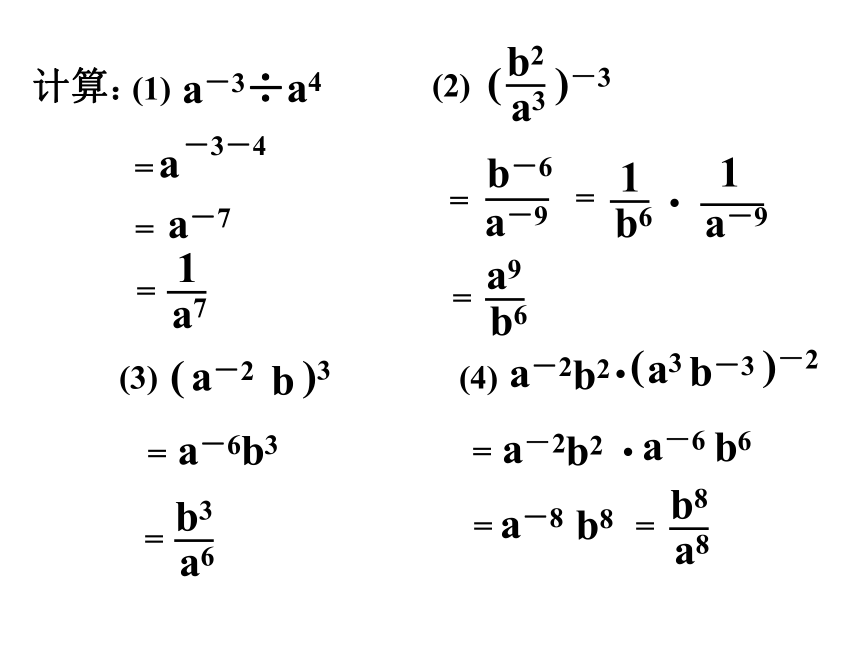



文档简介
(共25张PPT)
人教版 八年级上册
15. 2. 3整数指数幂 (2)
教学目标:
1.了解负整数指数幂的意义.
2.了解整数指数幂的性质并能运用它进行计算.
3.会利用10的负整数次幂,用科学记数法表示一
些小于1 的正数.
教学重点:
幂的性质(指数为全体整数),并会用于计算.用科学记数法表示一些小于1 的正数.
课件说明
(1) am an=am+n (m,n都是整数).
(2) (am)n=amn (m,n都是整数).
(3) (ab)n=anbn (n为整数).
(4) am÷an=am-n (a≠0,m,n都为整数).
(5) ( )n
a
b
=
an
bn
(n为整数).
有关幂的运算的性质
(6) a0=1 (a≠0).
(7)
a-n
=
1
an
(a≠0).
复习旧知
(1) = ____, = ;
(2) = ____, = ____;
(3) = ____, = ____.
填空:
80
5-2
(-8)0
m0
(-4)-2
1-2
1
1
1
1
25
1
16
1
(-4)-2
=
(-4)2
1
b-6
a-9
(2)
( )-3
b2
a3
(3)
( )3
a-2
b
(4)
a-2
b2
( )-2
b-3
a3
计算:
=
(1)
a-3
a4
÷
a
-3-4
=
a-7
=
1
a7
=
1
b6
=
a-9
1
=
a9
b6
=
a-6b3
b3
a6
=
=
a-2
b2
a-6
b6
=
a-8
b8
b8
a8
=
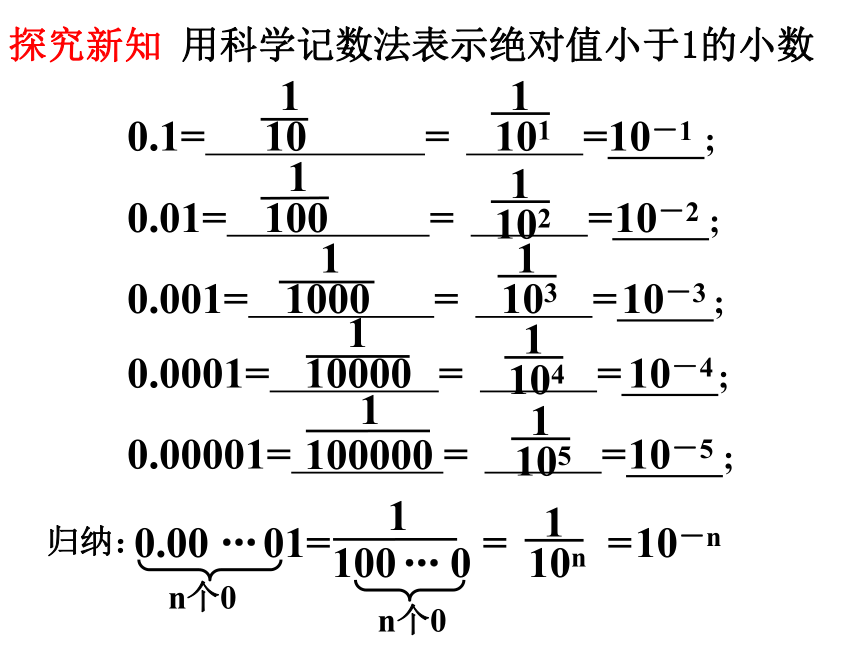
0.00001= = = ;
0.1= = = ;
0.01= = = ;
0.0001= = = ;
0.00 01= = =
0.001= = = ;
归纳:
10-1
10-2
10-3
10-4
10-5
10-n
1
10
1
101
100
1
1
102
1000
1
1
103
10000
1
100000
1
1
104
1
105
1
10n
100 0
1
● ● ●
● ● ●
n个0
n个0
用科学记数法表示绝对值小于1的小数
探究新知
0.000 098 2=
0.003 5=
规律:
用科学记数法表示一个小于1的正小数,从小数点前的0算起至小数点后第一个非0数字前有几个0,10的指数就是负几.
如何用科学记数法表示0.003 5和0.000 098 2呢?
观察这两个等式,看看10的指数与什么有关?
3.5×0.001
=
9.82×0.000 01
3.5×
=9.82×
10-3
10-5
解:(1) 0.3=
例2 用科学记数法表示下列各数:
(1) 0.3;(2)-0.000 78;(3)0.000 020 09.
3×
10-1 ;
(2) -0.000 78=
-7.8×
(3) 0.000 020 09=
10-4 ;
2.009×
10-5.
例题解析
用科学记数法表示下列各数:
(1)0.000 01; (2)0.001 2;
(3)0.000 000 345; (4)0.000 000 010 8.
练习巩固
解:(1) 0.000 01 = 1×10-5 ;
(2) 0.001 2 = 1.2×10-3 ;
(3) 0.000 000 345 = 3.45×10-7;
(4) 0.000 000 010 8 =1.08×10-8.
(2)(2×10-6)2÷(10-4)3.
(1)(2×10-6)×(3.2×103);
解:
(1)
(2×10-6)×(3.2×103)
=
(2×3.2 )×(10 -6 ×103)
6.2×10 -3
=
(2)
(2×10-6)2 ÷(10-4)3
=
4×10-12 ÷10-12
=
4
练习巩固
计算:
解:1 mm =10-3 m,1 nm =10-9 m.
答:1 mm3 的空间可以放1018个1 nm3 的物体.
例 纳米(nm)是非常小的长度单位,1 nm =10-9 m.
把1 nm3 的物体放到乒乓球上,就如同把乒乓球放到地
球上.1 mm3 的空间可以放多少个1 nm3 的物体.(物体之
间的间隙忽略不计)?
(10-3 )3
(10-9 )3
÷
=
10-9
÷
10-27
=
10-9-(-27)
=
1018
1.已知1纳米=0.000 000 001米,则2023纳米
用科学记数法表示为 ( ).
A. 20.23×10-7 B. 2.023×10-7
C. 2.023×10-6 D. 0.2023×10-5
练习巩固
2.一粒大米的质量约为0.000 02165千克,将
0.000 02165用科学记数法表示为 .
2.165×10-5
B
(1)本节课学习了哪些主要内容?
(2)整数指数幂的运算性质与正整数指数幂的运算
性质有什么区别和联系?
课堂小结
1.用科学记数法表示0.000203为 ( ).
A. 2.03×10-3 B. 2.03×10-4
C. 2.03×10-5 D. 2. 03×10-6
巩固提高
2.数1.24×10-2 用小数表示为 ( ).
A. 0.00124 B. 0.124
C. 0.0124 D. -0.124
B
D
3.将-2.02×10-3用小数表示为 ( ).
A. 0.000202 B. - 0.0202
C. 0.00202 D. -0.00202
4.下列各数中,最小的数是( ).
A. 9.5×10-9 B. 2.5×10-9
C. 9.5×10-8 D. 2. 5×10-8
D
B
5.计算3.82×10-8- 3.7×10-8 ,结果用科学
记数法表示为 ( ).
A. 0.12×10-8 B. 0.12×10-7
C. 1.2×10-9 D. 1. 2×10-8
C
6.下列各数中表示正确的是( ).
A. 57 000 000=57×108
B. 0.0158(用四舍五入法精确到0.001) ≈0.015
C. 1.804(用四舍五入法精确到十分位) ≈1.8
D. 0.000 025 7=2. 57×10-4
C
7.研究发现,银原子的半径约是 0.00015 微米,把
0.00015 这个数字用 科学计数法表示应是( ).
A.1.5×10-4 B.1.5×10-5
C.15×10-5 D.15×10-6
A
8.某种病毒的直径约为0.000 000 081米,将
0.000 000 081用科学记数法表示为 .
8.1×10-8
9.每立方厘米的空气质量约为1.239×10-3 g,
用小数表示为 g.
0.001239
10.用科学记数法表示下列各数:
(1)0.000 07; (2) -0.004 023.
解:(1) 0.000 07 = 7×10-5 ;
(2) -0.004 023 = -4.023×10-3 .
解:
11.水是由氢、氧两种元素组成的,1个氢原子的质量为1.674×10-27kg,1个氧原子的质量为2.657×10-26kg.1个氢原子与1个氧原子的质量哪个大
÷
=
10-26
÷
10-27
≈1.59
10-26-(-27)
>1
≈15.9
1.674×10-27
2.657×10-26
2.657
1.674
×
÷
×
∴1个氧原子比1个氢原子的质量大.
解:
12.雷达发出的微波以3×105km/s的速度射向飞机,飞机再将微波反射回来,经12.6微秒后雷达站收到反射微波,试问飞机与雷达站的距离是多少千米?
=
18.9×10-1
=1. 89
12.6×10-6
3×105
×
×
答:飞机与雷达站的距离是1.89千米.
(千米)
1
2
1秒=1 000 000微秒
今天作业
课本P147页第8、9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
15. 2. 3整数指数幂 (2)
教学目标:
1.了解负整数指数幂的意义.
2.了解整数指数幂的性质并能运用它进行计算.
3.会利用10的负整数次幂,用科学记数法表示一
些小于1 的正数.
教学重点:
幂的性质(指数为全体整数),并会用于计算.用科学记数法表示一些小于1 的正数.
课件说明
(1) am an=am+n (m,n都是整数).
(2) (am)n=amn (m,n都是整数).
(3) (ab)n=anbn (n为整数).
(4) am÷an=am-n (a≠0,m,n都为整数).
(5) ( )n
a
b
=
an
bn
(n为整数).
有关幂的运算的性质
(6) a0=1 (a≠0).
(7)
a-n
=
1
an
(a≠0).
复习旧知
(1) = ____, = ;
(2) = ____, = ____;
(3) = ____, = ____.
填空:
80
5-2
(-8)0
m0
(-4)-2
1-2
1
1
1
1
25
1
16
1
(-4)-2
=
(-4)2
1
b-6
a-9
(2)
( )-3
b2
a3
(3)
( )3
a-2
b
(4)
a-2
b2
( )-2
b-3
a3
计算:
=
(1)
a-3
a4
÷
a
-3-4
=
a-7
=
1
a7
=
1
b6
=
a-9
1
=
a9
b6
=
a-6b3
b3
a6
=
=
a-2
b2
a-6
b6
=
a-8
b8
b8
a8
=
0.00001= = = ;
0.1= = = ;
0.01= = = ;
0.0001= = = ;
0.00 01= = =
0.001= = = ;
归纳:
10-1
10-2
10-3
10-4
10-5
10-n
1
10
1
101
100
1
1
102
1000
1
1
103
10000
1
100000
1
1
104
1
105
1
10n
100 0
1
● ● ●
● ● ●
n个0
n个0
用科学记数法表示绝对值小于1的小数
探究新知
0.000 098 2=
0.003 5=
规律:
用科学记数法表示一个小于1的正小数,从小数点前的0算起至小数点后第一个非0数字前有几个0,10的指数就是负几.
如何用科学记数法表示0.003 5和0.000 098 2呢?
观察这两个等式,看看10的指数与什么有关?
3.5×0.001
=
9.82×0.000 01
3.5×
=9.82×
10-3
10-5
解:(1) 0.3=
例2 用科学记数法表示下列各数:
(1) 0.3;(2)-0.000 78;(3)0.000 020 09.
3×
10-1 ;
(2) -0.000 78=
-7.8×
(3) 0.000 020 09=
10-4 ;
2.009×
10-5.
例题解析
用科学记数法表示下列各数:
(1)0.000 01; (2)0.001 2;
(3)0.000 000 345; (4)0.000 000 010 8.
练习巩固
解:(1) 0.000 01 = 1×10-5 ;
(2) 0.001 2 = 1.2×10-3 ;
(3) 0.000 000 345 = 3.45×10-7;
(4) 0.000 000 010 8 =1.08×10-8.
(2)(2×10-6)2÷(10-4)3.
(1)(2×10-6)×(3.2×103);
解:
(1)
(2×10-6)×(3.2×103)
=
(2×3.2 )×(10 -6 ×103)
6.2×10 -3
=
(2)
(2×10-6)2 ÷(10-4)3
=
4×10-12 ÷10-12
=
4
练习巩固
计算:
解:1 mm =10-3 m,1 nm =10-9 m.
答:1 mm3 的空间可以放1018个1 nm3 的物体.
例 纳米(nm)是非常小的长度单位,1 nm =10-9 m.
把1 nm3 的物体放到乒乓球上,就如同把乒乓球放到地
球上.1 mm3 的空间可以放多少个1 nm3 的物体.(物体之
间的间隙忽略不计)?
(10-3 )3
(10-9 )3
÷
=
10-9
÷
10-27
=
10-9-(-27)
=
1018
1.已知1纳米=0.000 000 001米,则2023纳米
用科学记数法表示为 ( ).
A. 20.23×10-7 B. 2.023×10-7
C. 2.023×10-6 D. 0.2023×10-5
练习巩固
2.一粒大米的质量约为0.000 02165千克,将
0.000 02165用科学记数法表示为 .
2.165×10-5
B
(1)本节课学习了哪些主要内容?
(2)整数指数幂的运算性质与正整数指数幂的运算
性质有什么区别和联系?
课堂小结
1.用科学记数法表示0.000203为 ( ).
A. 2.03×10-3 B. 2.03×10-4
C. 2.03×10-5 D. 2. 03×10-6
巩固提高
2.数1.24×10-2 用小数表示为 ( ).
A. 0.00124 B. 0.124
C. 0.0124 D. -0.124
B
D
3.将-2.02×10-3用小数表示为 ( ).
A. 0.000202 B. - 0.0202
C. 0.00202 D. -0.00202
4.下列各数中,最小的数是( ).
A. 9.5×10-9 B. 2.5×10-9
C. 9.5×10-8 D. 2. 5×10-8
D
B
5.计算3.82×10-8- 3.7×10-8 ,结果用科学
记数法表示为 ( ).
A. 0.12×10-8 B. 0.12×10-7
C. 1.2×10-9 D. 1. 2×10-8
C
6.下列各数中表示正确的是( ).
A. 57 000 000=57×108
B. 0.0158(用四舍五入法精确到0.001) ≈0.015
C. 1.804(用四舍五入法精确到十分位) ≈1.8
D. 0.000 025 7=2. 57×10-4
C
7.研究发现,银原子的半径约是 0.00015 微米,把
0.00015 这个数字用 科学计数法表示应是( ).
A.1.5×10-4 B.1.5×10-5
C.15×10-5 D.15×10-6
A
8.某种病毒的直径约为0.000 000 081米,将
0.000 000 081用科学记数法表示为 .
8.1×10-8
9.每立方厘米的空气质量约为1.239×10-3 g,
用小数表示为 g.
0.001239
10.用科学记数法表示下列各数:
(1)0.000 07; (2) -0.004 023.
解:(1) 0.000 07 = 7×10-5 ;
(2) -0.004 023 = -4.023×10-3 .
解:
11.水是由氢、氧两种元素组成的,1个氢原子的质量为1.674×10-27kg,1个氧原子的质量为2.657×10-26kg.1个氢原子与1个氧原子的质量哪个大
÷
=
10-26
÷
10-27
≈1.59
10-26-(-27)
>1
≈15.9
1.674×10-27
2.657×10-26
2.657
1.674
×
÷
×
∴1个氧原子比1个氢原子的质量大.
解:
12.雷达发出的微波以3×105km/s的速度射向飞机,飞机再将微波反射回来,经12.6微秒后雷达站收到反射微波,试问飞机与雷达站的距离是多少千米?
=
18.9×10-1
=1. 89
12.6×10-6
3×105
×
×
答:飞机与雷达站的距离是1.89千米.
(千米)
1
2
1秒=1 000 000微秒
今天作业
课本P147页第8、9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
