人教版新教材必修一 3.4 动态三角形练习专题(含答案)
文档属性
| 名称 | 人教版新教材必修一 3.4 动态三角形练习专题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 683.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-25 16:27:50 | ||
图片预览


文档简介
人教版新教材必修一动态三角形练习专题(含答案)
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共60.0分)
如图所示,用长为的轻绳悬挂一质量为的小球,对小球再施加一个力,使绳与竖直方向成角并绷紧,小球处于静止状态,重力加速度大小为,此力的最小值为( )
A. B. C. D.
如图甲,一重物用细绳悬挂于点,用水平绳绑住绳的点,牵引至图示位置保持静止。现保持点的位置不变,改变绳牵引的方向,其拉力随旋转角度的变化如图乙所示,则重物的重力为( )
A. B. C. D.
如图所示,半圆形框架竖直放置在粗糙的水平地面上,一质量为的光滑小球在水平外力的作用下处于静止状态,与圆心的连线与水平面的夹角为,将力在竖直面内沿顺时针方向缓慢地转过,框架与小球始终保持静止状态.在此过程中下列说法正确的是重力加速度为( )
A. 框架对小球的支持力先减小后增大 B. 拉力的最小值为
C. 地面对框架的摩擦力先减小后增大 D. 框架对地面的压力先增大后减小
如图所示,挡板和竖直墙壁之间夹有质量为的小球,当挡板和竖直墙壁之间的夹角从缓慢减小至的过程中,以下说法正确的是( )
A. 小球对挡板的压力先增大后减小 B. 小球对挡板的压力逐渐减小
C. 小球对竖直墙壁的弹力逐渐增大 D. 小球对竖直墙壁的弹力先减小后增大
一物体静止在斜面上,如图所示.当斜面的倾角缓慢增大而物体仍静止在斜面上,此过程中
物体所受重力和静摩擦力的合力不变
物体所受支持力和静摩擦力的合力不变
物体所受重力和支持力的合力逐渐增大
物体所受重力、支持力和静摩擦力的合力逐渐增大
A. B. C. D.
瑜伽是一种深受当代年轻人喜爱的健身运动。某个瑜伽练习者按图示方向缓慢打开双腿。假设在该过程中,每只脚受到的支持力大小为,每只脚受到的摩擦力大小为。下列说法正确的是( )
A. 不变,变大
B. 不变,变小
C. 变大,不变
D. 变大,变大
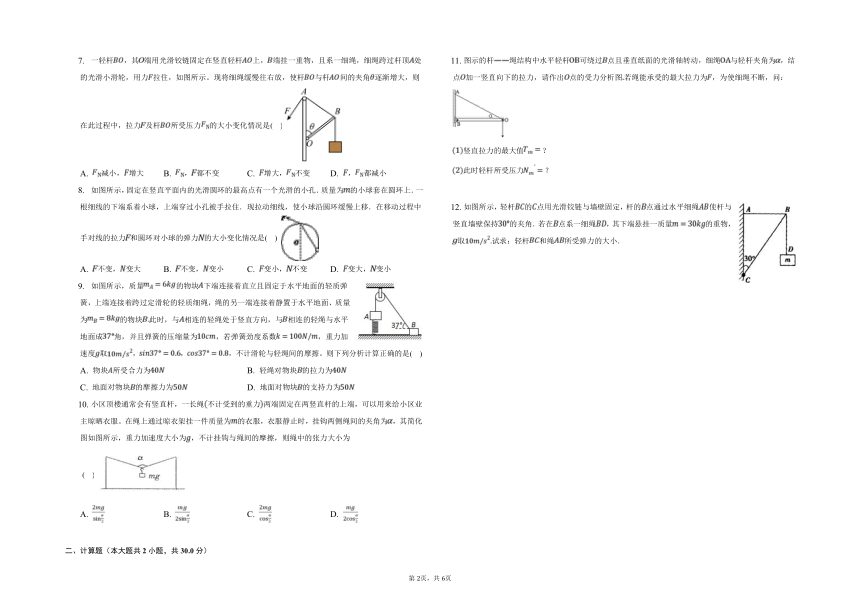
一轻杆,其端用光滑铰链固定在竖直轻杆上,端挂一重物,且系一细绳,细绳跨过杆顶处的光滑小滑轮,用力拉住,如图所示。现将细绳缓慢往右放,使杆与杆间的夹角逐渐增大,则在此过程中,拉力及杆所受压力的大小变化情况是( )
A. 减小,增大 B. ,都不变 C. 增大,不变 D. ,都减小
如图所示,固定在竖直平面内的光滑圆环的最高点有一个光滑的小孔.质量为的小球套在圆环上.一根细线的下端系着小球,上端穿过小孔被手拉住.现拉动细线,使小球沿圆环缓慢上移.在移动过程中手对线的拉力和圆环对小球的弹力的大小变化情况是( )
A. 不变,变大 B. 不变,变小 C. 变小,不变 D. 变大,变小
如图所示,质量的物块下端连接着直立且固定于水平地面的轻质弹簧,上端连接着跨过定滑轮的轻质细绳,绳的另一端连接着静置于水平地面、质量为的物块此时,与相连的轻绳处于竖直方向,与相连的轻绳与水平地面成角,并且弹簧的压缩量为,若弹簧劲度系数,重力加速度取,,,不计滑轮与轻绳间的摩擦。则下列分析计算正确的是( )
A. 物块所受合力为 B. 轻绳对物块的拉力为
C. 地面对物块的摩擦力为 D. 地面对物块的支持力为
小区顶楼通常会有竖直杆,一长绳不计受到的重力两端固定在两竖直杆的上端,可以用来给小区业主晾晒衣服。在绳上通过晾衣架挂一件质量为的衣服,衣服静止时,挂钩两侧绳间的夹角为,其简化图如图所示,重力加速度大小为,不计挂钩与绳间的摩擦,则绳中的张力大小为( )
A. B. C. D.
二、计算题(本大题共2小题,共30.0分)
图示的杆绳结构中水平轻杆可绕过点且垂直纸面的光滑轴转动,细绳与轻杆夹角为,结点加一竖直向下的拉力,请作出点的受力分析图若绳能承受的最大拉力为,为使细绳不断,问:
竖直拉力的最大值?
此时轻杆所受压力?
如图所示,轻杆的点用光滑铰链与墙壁固定,杆的点通过水平细绳使杆与竖直墙壁保持的夹角.若在点系一细绳,其下端悬挂一质量的重物,取试求:轻杆和绳所受弹力的大小.
答案和解析
1.【答案】
【解析】
【分析】
以小球为研究对象,分析受力情况:重力,绳的拉力和力,根据平衡条件的推论可知,绳的拉力和力的合力大小等于,方向竖直向上,保持不变,根据作图法,确定力最小时的方向,再根据平衡条件求出的最小值。
本题是三力平衡中的动态分析问题,关键是根据平衡条件并结合合成法作图分析。
【解答】
以小球为研究对象,小球受重力,绳的拉力和力,根据平衡条件,应有与合力与等大反向,即与的合力为;如图所示,在合力一定,其一分力方向一定的前提下,另一分力的最小值由三角形定则可知应垂直绳所在直线,故;故A正确,故BCD错误。
故选A。
2.【答案】
【解析】
【分析】
通过对节点进行受力分析,根据三力平衡的特点求解重力。
本题主要考查平衡条件和平衡状态,关键在于利用矢量三角形的性质求解。
【解答】
对节点,由于三力平衡,则三个力组成闭合三角形,由于保持点不变,由矢量三角形作出力的三角形,如图所示:
由图乙可知,由于当时,拉力最小,此时则有,解得重力,故ACD错误,故B正确。
3.【答案】
【解析】
【分析】
以小球为研究对象,分析受力情况,作出受力示意图,根据平衡条件分析小球受力变化情况,再以整体为研究对象,分析框架的受力情况。
本题主要是考查了共点力的平衡问题,解答此类问题的一般步骤是:确定研究对象、进行受力分析、利用平行四边形法则进行力的合成或者是正交分解法进行力的分解,然后在坐标轴上建立平衡方程进行解答,本题也可以利用图解法来分析。
【解答】
以小球为研究对象,分析受力情况,作出受力示意力图,如图所示:
根据几何关系可知,用顺时针转动至竖直向上之前,支持力逐渐减小,先减小后增大,当的方向沿圆的切线方向向上时,最小,此时:故A错误,B正确;
C.以框架与小球组成的整体为研究对象,整体受到重力、地面的支持力、地面的摩擦力以及力的作用;由图可知,在顺时针方向转动的过程中,沿水平方向的分力逐渐减小,所以地面对框架的摩擦力始终在减小。故C错误;
D.以框架与小球组成的整体为研究对象,整体受到重力、地面的支持力、地面的摩擦力以及力的作用;由图可知,在顺时针方向转动的过程中,沿竖直方向的分力逐渐增大,所以地面对框架的支持力始终在减小。故D错误。
故选B。
4.【答案】
【解析】解:以小球为研究对象,处于平衡状态,根据受力平衡,有:
由图可知,、挡板给球的支持力逐渐增大,根据牛顿第三定律可知小球对挡板的压力逐渐增大,AB错误;
、墙壁给球的压力逐渐增大,所以挡板给球的支持力逐渐增大,根据牛顿第三定律可知小球对竖直墙壁的弹力逐渐增大,C正确、D错误;
故选:。
对球进行正确受力分析,把握其受力特点:一个力大小和方向不变重力,一个力方向不变墙给球的支持力,另一个力的大小、方向均发生变化挡板给球的作用力,对于这类动态平衡问题,即可以采用“图解法”进行.
本题主要是考查了共点力的平衡问题,解答此类问题的一般步骤是:确定研究对象、进行受力分析、利用平行四边形法则进行力的合成或者是正交分解法进行力的分解,然后在坐标轴上建立平衡方程进行解答.本题是利用图解法来分析的.
5.【答案】
【解析】
【分析】
本题主要是考查了共点力的平衡问题,当三个力平衡时合力为零,任何两个力的合力与第三个力等大反向。
本题的关键是首先对物体受力分析,根据平衡条件求出每个分力的大小,然后根据合力与分力的等效性即可求解。
【解答】
由于重力与静摩擦力的合力等于支持力,而,由于增大减小,故错误;
由于支持力与静摩擦力的合力等于重力应不变,故正确;
物体受到向下的重力、垂直斜面向上的支持力和沿斜面向上的静摩擦力,根据平衡条件可知,重力与支持力的合力应等于静摩擦力,再由可知静摩擦力增大,则物体所受重力和支持力的合力逐渐增大,故正确;
根据平衡条件可知重力、支持力、静摩擦力的合力应为零,故错误。
故正确的是: ,故B正确,ACD错误。
故选:。
6.【答案】
【解析】解:以其中一只脚为研究对象,受到地面的支持力和摩擦力、腿对它的作用力,如图所示:
设人的质量为,以人为研究对象,竖直方向根据平衡条件可得:,解得:;
设每只腿与竖直方向的夹角为,以其中一只脚为研究对象,根据平衡条件可得:。
瑜伽练习者按图示方向缓慢打开双腿,支持力不变、增大,则增大,故A正确、BCD错误。
故选:。
以人为研究对象,竖直方向根据平衡条件分析支持力的变化;以其中一只脚为研究对象,根据平衡条件分析摩擦力的变化。
本题主要是考查了共点力的平衡问题,解答此类问题的一般步骤是:确定研究对象、进行受力分析、利用平行四边形法则进行力的合成或者是正交分解法进行力的分解,然后在坐标轴上建立平衡方程进行解答。
7.【答案】
【解析】解:设物体的重力为以点为研究对象,分析受力情况,作出力图,如图。
作出力与的合力,根据平衡条件得知,由∽得:
得到:
式中,、、不变,则保持不变。
同理:
得到:
,
式中,、不变,但是逐渐增大,所以逐渐变大。
故C正确,ABD错误。
故选:。
当细绳缓慢拉动时,整个装置处于动态平衡状态,以点为研究对象,分析受力情况,作出力图.根据平衡条件,运用三角形相似法,得出和与边长、、及物体重力的关系,再分析、的变化情况.
本题中涉及非直角三角形,运用几何知识研究力与边或角的关系,是常用的思路.
8.【答案】
【解析】
【分析】
对小球受力分析,作出力的平行四边形,同时作出与半径组成的图象;则可知两三角形相似,故由相似三角形知识可求得拉力及支持力。
本题考察了通过整体法判断外力,利用隔离法判断物体的内力的方法,相似三角形法在处理共点力的动态平衡时较为常见,当无法准确得出角边关系时,应考虑应用此法。
【解答】
这属于典型的动态三角形利用相似解决问题的题型,受力分析如图所示
力的三角形与空间三角形相似,重力相当于半径,支持力相当于半径,拉力相当于,由相似原理得:。随着圆环缓慢上移,减小,和、不变,缓慢运动相当于任何时刻圆环处于平衡状态,所以可知减小,不变,故C正确,ABD错误。
故选C。
9.【答案】
【解析】解:、物块处于静止状态,受到的合力为零,故A错误;
B、弹簧压缩,根据胡克定律可知,弹簧弹力,弹力向上,绳子拉力,故B错误;
、处于静止状态,受力平衡,对受力分析,根据平衡条件,地面对物块的支持力;地面对的摩擦力,故C错误,D正确。
故选D。
根据胡克定律求出弹簧弹力,根据物体受力平衡列式求出绳子的拉力,物体均处于静止状态,受力平衡,根据平衡条件求出地面对的支持力以及摩擦力的表达式,进而求解,
本题主要考查了共点力平衡条件的直接应用,要求能正确分析物体的受力情况,注意整体法和隔离法在解题中的应用。
10.【答案】
【解析】
【分析】
本题主要考查了共点力的平衡问题,对于该题关键是知道挂钩两侧绳子相当于活结问题,两侧绳子拉力相等,根据平衡条件计算。
【解答】
由于挂钩两侧绳子拉力相等,故两侧绳子与竖直方向夹角相等,均为,设绳中张力为,根据平衡条件有:,解得:,故D正确。
11.【答案】解:点受到竖直向下的拉力、绳子的拉力和杆的支持力作用,如图
根据几何关系可得竖直拉力的最大值:;
根据平衡条件可得:
根据牛顿第三定律可得:
解得:。
答:竖直拉力的最大值为;
此时轻杆所受压力为。
【解析】以点为研究对象,根据受力情况画出受力示意图,再根据几何关系进行解答。
本题主要是考查了共点力的平衡问题,解答此类问题的一般步骤是:确定研究对象、进行受力分析、利用平行四边形法则进行力的合成或者是正交分解法进行力的分解,然后在坐标轴上建立平衡方程进行解答。
12.【答案】解:将绳子对点的重力分解为沿方向和沿两个方向的分力,作出力的分解图,则有
绳子的拉力
杆中的弹力
答:轻杆和绳所受弹力的大小分别为和.
【解析】将绳子对点的重力分解为沿方向和沿两个方向的分力,作出力的分解图,由数学知识求解杆中的弹力和绳中的张力大小.
本题运用分解法处理共点力问题,也可以根据正交分解法和合成法研究.
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共60.0分)
如图所示,用长为的轻绳悬挂一质量为的小球,对小球再施加一个力,使绳与竖直方向成角并绷紧,小球处于静止状态,重力加速度大小为,此力的最小值为( )
A. B. C. D.
如图甲,一重物用细绳悬挂于点,用水平绳绑住绳的点,牵引至图示位置保持静止。现保持点的位置不变,改变绳牵引的方向,其拉力随旋转角度的变化如图乙所示,则重物的重力为( )
A. B. C. D.
如图所示,半圆形框架竖直放置在粗糙的水平地面上,一质量为的光滑小球在水平外力的作用下处于静止状态,与圆心的连线与水平面的夹角为,将力在竖直面内沿顺时针方向缓慢地转过,框架与小球始终保持静止状态.在此过程中下列说法正确的是重力加速度为( )
A. 框架对小球的支持力先减小后增大 B. 拉力的最小值为
C. 地面对框架的摩擦力先减小后增大 D. 框架对地面的压力先增大后减小
如图所示,挡板和竖直墙壁之间夹有质量为的小球,当挡板和竖直墙壁之间的夹角从缓慢减小至的过程中,以下说法正确的是( )
A. 小球对挡板的压力先增大后减小 B. 小球对挡板的压力逐渐减小
C. 小球对竖直墙壁的弹力逐渐增大 D. 小球对竖直墙壁的弹力先减小后增大
一物体静止在斜面上,如图所示.当斜面的倾角缓慢增大而物体仍静止在斜面上,此过程中
物体所受重力和静摩擦力的合力不变
物体所受支持力和静摩擦力的合力不变
物体所受重力和支持力的合力逐渐增大
物体所受重力、支持力和静摩擦力的合力逐渐增大
A. B. C. D.
瑜伽是一种深受当代年轻人喜爱的健身运动。某个瑜伽练习者按图示方向缓慢打开双腿。假设在该过程中,每只脚受到的支持力大小为,每只脚受到的摩擦力大小为。下列说法正确的是( )
A. 不变,变大
B. 不变,变小
C. 变大,不变
D. 变大,变大
一轻杆,其端用光滑铰链固定在竖直轻杆上,端挂一重物,且系一细绳,细绳跨过杆顶处的光滑小滑轮,用力拉住,如图所示。现将细绳缓慢往右放,使杆与杆间的夹角逐渐增大,则在此过程中,拉力及杆所受压力的大小变化情况是( )
A. 减小,增大 B. ,都不变 C. 增大,不变 D. ,都减小
如图所示,固定在竖直平面内的光滑圆环的最高点有一个光滑的小孔.质量为的小球套在圆环上.一根细线的下端系着小球,上端穿过小孔被手拉住.现拉动细线,使小球沿圆环缓慢上移.在移动过程中手对线的拉力和圆环对小球的弹力的大小变化情况是( )
A. 不变,变大 B. 不变,变小 C. 变小,不变 D. 变大,变小
如图所示,质量的物块下端连接着直立且固定于水平地面的轻质弹簧,上端连接着跨过定滑轮的轻质细绳,绳的另一端连接着静置于水平地面、质量为的物块此时,与相连的轻绳处于竖直方向,与相连的轻绳与水平地面成角,并且弹簧的压缩量为,若弹簧劲度系数,重力加速度取,,,不计滑轮与轻绳间的摩擦。则下列分析计算正确的是( )
A. 物块所受合力为 B. 轻绳对物块的拉力为
C. 地面对物块的摩擦力为 D. 地面对物块的支持力为
小区顶楼通常会有竖直杆,一长绳不计受到的重力两端固定在两竖直杆的上端,可以用来给小区业主晾晒衣服。在绳上通过晾衣架挂一件质量为的衣服,衣服静止时,挂钩两侧绳间的夹角为,其简化图如图所示,重力加速度大小为,不计挂钩与绳间的摩擦,则绳中的张力大小为( )
A. B. C. D.
二、计算题(本大题共2小题,共30.0分)
图示的杆绳结构中水平轻杆可绕过点且垂直纸面的光滑轴转动,细绳与轻杆夹角为,结点加一竖直向下的拉力,请作出点的受力分析图若绳能承受的最大拉力为,为使细绳不断,问:
竖直拉力的最大值?
此时轻杆所受压力?
如图所示,轻杆的点用光滑铰链与墙壁固定,杆的点通过水平细绳使杆与竖直墙壁保持的夹角.若在点系一细绳,其下端悬挂一质量的重物,取试求:轻杆和绳所受弹力的大小.
答案和解析
1.【答案】
【解析】
【分析】
以小球为研究对象,分析受力情况:重力,绳的拉力和力,根据平衡条件的推论可知,绳的拉力和力的合力大小等于,方向竖直向上,保持不变,根据作图法,确定力最小时的方向,再根据平衡条件求出的最小值。
本题是三力平衡中的动态分析问题,关键是根据平衡条件并结合合成法作图分析。
【解答】
以小球为研究对象,小球受重力,绳的拉力和力,根据平衡条件,应有与合力与等大反向,即与的合力为;如图所示,在合力一定,其一分力方向一定的前提下,另一分力的最小值由三角形定则可知应垂直绳所在直线,故;故A正确,故BCD错误。
故选A。
2.【答案】
【解析】
【分析】
通过对节点进行受力分析,根据三力平衡的特点求解重力。
本题主要考查平衡条件和平衡状态,关键在于利用矢量三角形的性质求解。
【解答】
对节点,由于三力平衡,则三个力组成闭合三角形,由于保持点不变,由矢量三角形作出力的三角形,如图所示:
由图乙可知,由于当时,拉力最小,此时则有,解得重力,故ACD错误,故B正确。
3.【答案】
【解析】
【分析】
以小球为研究对象,分析受力情况,作出受力示意图,根据平衡条件分析小球受力变化情况,再以整体为研究对象,分析框架的受力情况。
本题主要是考查了共点力的平衡问题,解答此类问题的一般步骤是:确定研究对象、进行受力分析、利用平行四边形法则进行力的合成或者是正交分解法进行力的分解,然后在坐标轴上建立平衡方程进行解答,本题也可以利用图解法来分析。
【解答】
以小球为研究对象,分析受力情况,作出受力示意力图,如图所示:
根据几何关系可知,用顺时针转动至竖直向上之前,支持力逐渐减小,先减小后增大,当的方向沿圆的切线方向向上时,最小,此时:故A错误,B正确;
C.以框架与小球组成的整体为研究对象,整体受到重力、地面的支持力、地面的摩擦力以及力的作用;由图可知,在顺时针方向转动的过程中,沿水平方向的分力逐渐减小,所以地面对框架的摩擦力始终在减小。故C错误;
D.以框架与小球组成的整体为研究对象,整体受到重力、地面的支持力、地面的摩擦力以及力的作用;由图可知,在顺时针方向转动的过程中,沿竖直方向的分力逐渐增大,所以地面对框架的支持力始终在减小。故D错误。
故选B。
4.【答案】
【解析】解:以小球为研究对象,处于平衡状态,根据受力平衡,有:
由图可知,、挡板给球的支持力逐渐增大,根据牛顿第三定律可知小球对挡板的压力逐渐增大,AB错误;
、墙壁给球的压力逐渐增大,所以挡板给球的支持力逐渐增大,根据牛顿第三定律可知小球对竖直墙壁的弹力逐渐增大,C正确、D错误;
故选:。
对球进行正确受力分析,把握其受力特点:一个力大小和方向不变重力,一个力方向不变墙给球的支持力,另一个力的大小、方向均发生变化挡板给球的作用力,对于这类动态平衡问题,即可以采用“图解法”进行.
本题主要是考查了共点力的平衡问题,解答此类问题的一般步骤是:确定研究对象、进行受力分析、利用平行四边形法则进行力的合成或者是正交分解法进行力的分解,然后在坐标轴上建立平衡方程进行解答.本题是利用图解法来分析的.
5.【答案】
【解析】
【分析】
本题主要是考查了共点力的平衡问题,当三个力平衡时合力为零,任何两个力的合力与第三个力等大反向。
本题的关键是首先对物体受力分析,根据平衡条件求出每个分力的大小,然后根据合力与分力的等效性即可求解。
【解答】
由于重力与静摩擦力的合力等于支持力,而,由于增大减小,故错误;
由于支持力与静摩擦力的合力等于重力应不变,故正确;
物体受到向下的重力、垂直斜面向上的支持力和沿斜面向上的静摩擦力,根据平衡条件可知,重力与支持力的合力应等于静摩擦力,再由可知静摩擦力增大,则物体所受重力和支持力的合力逐渐增大,故正确;
根据平衡条件可知重力、支持力、静摩擦力的合力应为零,故错误。
故正确的是: ,故B正确,ACD错误。
故选:。
6.【答案】
【解析】解:以其中一只脚为研究对象,受到地面的支持力和摩擦力、腿对它的作用力,如图所示:
设人的质量为,以人为研究对象,竖直方向根据平衡条件可得:,解得:;
设每只腿与竖直方向的夹角为,以其中一只脚为研究对象,根据平衡条件可得:。
瑜伽练习者按图示方向缓慢打开双腿,支持力不变、增大,则增大,故A正确、BCD错误。
故选:。
以人为研究对象,竖直方向根据平衡条件分析支持力的变化;以其中一只脚为研究对象,根据平衡条件分析摩擦力的变化。
本题主要是考查了共点力的平衡问题,解答此类问题的一般步骤是:确定研究对象、进行受力分析、利用平行四边形法则进行力的合成或者是正交分解法进行力的分解,然后在坐标轴上建立平衡方程进行解答。
7.【答案】
【解析】解:设物体的重力为以点为研究对象,分析受力情况,作出力图,如图。
作出力与的合力,根据平衡条件得知,由∽得:
得到:
式中,、、不变,则保持不变。
同理:
得到:
,
式中,、不变,但是逐渐增大,所以逐渐变大。
故C正确,ABD错误。
故选:。
当细绳缓慢拉动时,整个装置处于动态平衡状态,以点为研究对象,分析受力情况,作出力图.根据平衡条件,运用三角形相似法,得出和与边长、、及物体重力的关系,再分析、的变化情况.
本题中涉及非直角三角形,运用几何知识研究力与边或角的关系,是常用的思路.
8.【答案】
【解析】
【分析】
对小球受力分析,作出力的平行四边形,同时作出与半径组成的图象;则可知两三角形相似,故由相似三角形知识可求得拉力及支持力。
本题考察了通过整体法判断外力,利用隔离法判断物体的内力的方法,相似三角形法在处理共点力的动态平衡时较为常见,当无法准确得出角边关系时,应考虑应用此法。
【解答】
这属于典型的动态三角形利用相似解决问题的题型,受力分析如图所示
力的三角形与空间三角形相似,重力相当于半径,支持力相当于半径,拉力相当于,由相似原理得:。随着圆环缓慢上移,减小,和、不变,缓慢运动相当于任何时刻圆环处于平衡状态,所以可知减小,不变,故C正确,ABD错误。
故选C。
9.【答案】
【解析】解:、物块处于静止状态,受到的合力为零,故A错误;
B、弹簧压缩,根据胡克定律可知,弹簧弹力,弹力向上,绳子拉力,故B错误;
、处于静止状态,受力平衡,对受力分析,根据平衡条件,地面对物块的支持力;地面对的摩擦力,故C错误,D正确。
故选D。
根据胡克定律求出弹簧弹力,根据物体受力平衡列式求出绳子的拉力,物体均处于静止状态,受力平衡,根据平衡条件求出地面对的支持力以及摩擦力的表达式,进而求解,
本题主要考查了共点力平衡条件的直接应用,要求能正确分析物体的受力情况,注意整体法和隔离法在解题中的应用。
10.【答案】
【解析】
【分析】
本题主要考查了共点力的平衡问题,对于该题关键是知道挂钩两侧绳子相当于活结问题,两侧绳子拉力相等,根据平衡条件计算。
【解答】
由于挂钩两侧绳子拉力相等,故两侧绳子与竖直方向夹角相等,均为,设绳中张力为,根据平衡条件有:,解得:,故D正确。
11.【答案】解:点受到竖直向下的拉力、绳子的拉力和杆的支持力作用,如图
根据几何关系可得竖直拉力的最大值:;
根据平衡条件可得:
根据牛顿第三定律可得:
解得:。
答:竖直拉力的最大值为;
此时轻杆所受压力为。
【解析】以点为研究对象,根据受力情况画出受力示意图,再根据几何关系进行解答。
本题主要是考查了共点力的平衡问题,解答此类问题的一般步骤是:确定研究对象、进行受力分析、利用平行四边形法则进行力的合成或者是正交分解法进行力的分解,然后在坐标轴上建立平衡方程进行解答。
12.【答案】解:将绳子对点的重力分解为沿方向和沿两个方向的分力,作出力的分解图,则有
绳子的拉力
杆中的弹力
答:轻杆和绳所受弹力的大小分别为和.
【解析】将绳子对点的重力分解为沿方向和沿两个方向的分力,作出力的分解图,由数学知识求解杆中的弹力和绳中的张力大小.
本题运用分解法处理共点力问题,也可以根据正交分解法和合成法研究.
第1页,共1页
