北师大版八年级数学上册《1.1.1勾股定理》教学课件(共19张PPT)
文档属性
| 名称 | 北师大版八年级数学上册《1.1.1勾股定理》教学课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 652.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 16:09:47 | ||
图片预览





文档简介
(共19张PPT)
第一章 勾股定理
1.1 探索勾股定理
第1课时 勾股定理
学习目标
1.经历探索勾股定理的过程,了解勾股定理的探究方法;
2.掌握勾股定理,并能运用勾股定理解决一些简单问题.
勾股定理是一个古老的定理,人类很早就发现了这个定理.
新知引入
一个直角三角形的两条直角边长分别是3和4,你知道它的第三边长吗?
实际上,利用勾股定理我们可以很容易地解决这个问题.
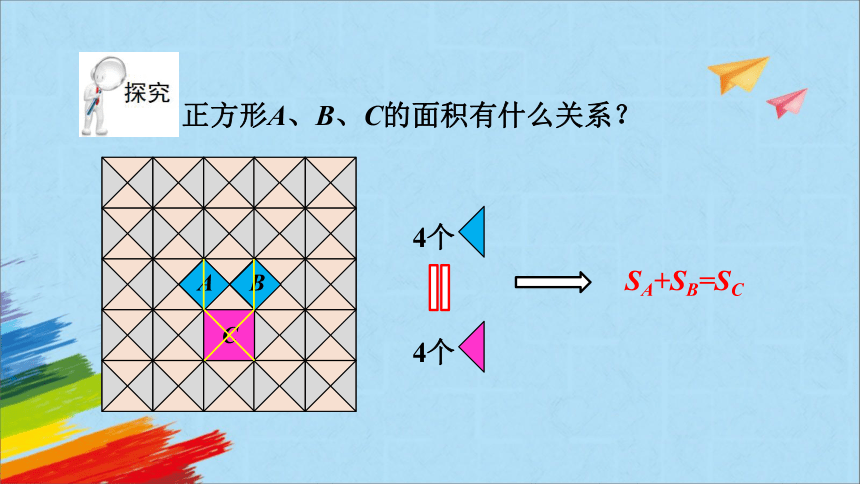
正方形A、B、C的面积有什么关系?
SA+SB=SC
A
B
C
4个
4个
A
B
C
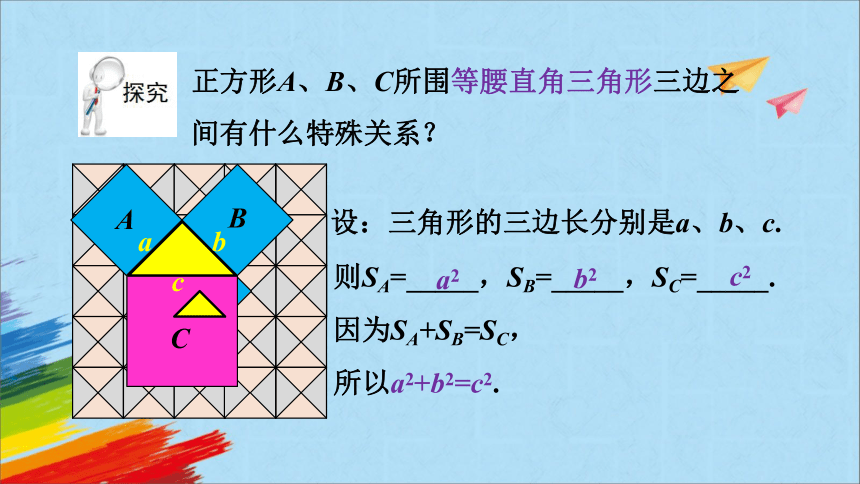
正方形A、B、C所围等腰直角三角形三边之间有什么特殊关系?
A
B
C
所以a2+b2=c2.
则SA=_____,SB=_____,SC=_____.
因为SA+SB=SC,
a2
b2
c2
a
b
c
设:三角形的三边长分别是a、b、c.
等腰直角三角形的三边关系:
两直角边的平方和等于斜边的平方.
归纳总结
A
C
B
A'
C'
B'
一般的直角三角形是否也具有“两直角边的平方和等于斜边的平方”这一性质呢?
(图中每个小方格代表一个单位面积)
图①
图②
A
C
B
正方形A中含有____个小正方形,即A的面积是_____.
正方形B中含有____个小正方形,即B的面积是_____.
正方形C中含有____个小正方形,即C的面积是_____.
观察:
4
4
9
9
正方形C的面积应该怎么计算呢?
图①
A
C
B
分“割”成若干个直角边为整数的三角形
SC=×2×3×4+1×1=13;
把C“补”成边长为5的正方形
SC=5×5-×2×3×4=13.
图①
A
C
B
正方形A中含有____个小正方形,即A的面积是_____.
正方形B中含有____个小正方形,即B的面积是_____.
正方形C中含有____个小正方形,即C的面积是_____.
观察:
4
4
9
9
13
13
图①
A'
C'
B'
观察:
正方形A'中含有____个小正方形,即A'的面积是_____.
正方形B'中含有____个小正方形,即B'的面积是_____.
正方形C'中含有____个小正方形,即C'的面积是_____.
16
16
9
9
25
25
图②
A的面积 (单位面积) B的面积 (单位面积) C的面积
(单位面积)
图①
图②
A、B、C面积关系 填表:
4
9
13
16
9
25
SA+SB=SC
归纳总结
勾股定理
直角三角形两直角边的平方和等于斜边的平方.如果用a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
趣味历史:勾股定理名字的来源
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦,勾股定理因此而得名.
例1 高为2.5 m的木梯,架在高为2.4 m的墙上(如图),这时梯脚与墙的距离是多少
解:在Rt△ABC中,根据勾股定理,得:
BC2=AB2-AC2=2.52-2.42=0.49,
所以BC=0.7.
即梯脚与墙的距离是0.7 m.
A
C
B
例2 求斜边长为17 cm、一条直角边长为15 cm的直角三角形的另一边长.
解:设另一条直角边长是x cm.
根据勾股定理,得:
152+ x2 =172,
则x2=172-152=289–225=64,
解得 x=±8(负值舍去),
所以另一直角边长为8 cm.
1.直角△ABC的两条直角边a=5,b=12,斜边c=______.
A
B
C
5
12
c
a
b
13
2.直角△ABC的一条直角边a=10,斜边c=26,则b=______.
A
B
C
10
26
c
a
b
24
课堂小结
勾股定理:
直角三角形两直角边的平方和等于斜边的平方.如果用a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
谢谢
第一章 勾股定理
1.1 探索勾股定理
第1课时 勾股定理
学习目标
1.经历探索勾股定理的过程,了解勾股定理的探究方法;
2.掌握勾股定理,并能运用勾股定理解决一些简单问题.
勾股定理是一个古老的定理,人类很早就发现了这个定理.
新知引入
一个直角三角形的两条直角边长分别是3和4,你知道它的第三边长吗?
实际上,利用勾股定理我们可以很容易地解决这个问题.
正方形A、B、C的面积有什么关系?
SA+SB=SC
A
B
C
4个
4个
A
B
C
正方形A、B、C所围等腰直角三角形三边之间有什么特殊关系?
A
B
C
所以a2+b2=c2.
则SA=_____,SB=_____,SC=_____.
因为SA+SB=SC,
a2
b2
c2
a
b
c
设:三角形的三边长分别是a、b、c.
等腰直角三角形的三边关系:
两直角边的平方和等于斜边的平方.
归纳总结
A
C
B
A'
C'
B'
一般的直角三角形是否也具有“两直角边的平方和等于斜边的平方”这一性质呢?
(图中每个小方格代表一个单位面积)
图①
图②
A
C
B
正方形A中含有____个小正方形,即A的面积是_____.
正方形B中含有____个小正方形,即B的面积是_____.
正方形C中含有____个小正方形,即C的面积是_____.
观察:
4
4
9
9
正方形C的面积应该怎么计算呢?
图①
A
C
B
分“割”成若干个直角边为整数的三角形
SC=×2×3×4+1×1=13;
把C“补”成边长为5的正方形
SC=5×5-×2×3×4=13.
图①
A
C
B
正方形A中含有____个小正方形,即A的面积是_____.
正方形B中含有____个小正方形,即B的面积是_____.
正方形C中含有____个小正方形,即C的面积是_____.
观察:
4
4
9
9
13
13
图①
A'
C'
B'
观察:
正方形A'中含有____个小正方形,即A'的面积是_____.
正方形B'中含有____个小正方形,即B'的面积是_____.
正方形C'中含有____个小正方形,即C'的面积是_____.
16
16
9
9
25
25
图②
A的面积 (单位面积) B的面积 (单位面积) C的面积
(单位面积)
图①
图②
A、B、C面积关系 填表:
4
9
13
16
9
25
SA+SB=SC
归纳总结
勾股定理
直角三角形两直角边的平方和等于斜边的平方.如果用a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
趣味历史:勾股定理名字的来源
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦,勾股定理因此而得名.
例1 高为2.5 m的木梯,架在高为2.4 m的墙上(如图),这时梯脚与墙的距离是多少
解:在Rt△ABC中,根据勾股定理,得:
BC2=AB2-AC2=2.52-2.42=0.49,
所以BC=0.7.
即梯脚与墙的距离是0.7 m.
A
C
B
例2 求斜边长为17 cm、一条直角边长为15 cm的直角三角形的另一边长.
解:设另一条直角边长是x cm.
根据勾股定理,得:
152+ x2 =172,
则x2=172-152=289–225=64,
解得 x=±8(负值舍去),
所以另一直角边长为8 cm.
1.直角△ABC的两条直角边a=5,b=12,斜边c=______.
A
B
C
5
12
c
a
b
13
2.直角△ABC的一条直角边a=10,斜边c=26,则b=______.
A
B
C
10
26
c
a
b
24
课堂小结
勾股定理:
直角三角形两直角边的平方和等于斜边的平方.如果用a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
谢谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
