北师大版八年级数学上册《1.1.2勾股定理的验证》教学课件(共17张PPT)
文档属性
| 名称 | 北师大版八年级数学上册《1.1.2勾股定理的验证》教学课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 929.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 11:52:04 | ||
图片预览




文档简介
(共17张PPT)
第一章 勾股定理
1.1 探索勾股定理
第2课时 勾股定理的验证
1.经历验证勾股定理的过程,进一步发展空间观念和推理能力;
2.掌握勾股定理,并能运用勾股定理解决一些实际问题.
学习目标
回顾复习
勾股定理的内容是什么?
直角三角形两直角边的平方和等于斜边的平方.如果用a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
上节课我们仅仅是通过对具体的直角三角形数格子探索发现了勾股定理.
提出问题
事实上,现在已经有几百种勾股定理的验证方法,这节课我们也将要验证勾股定理.
对任意的直角三角形,勾股定理是否成立呢?这需要进一步验证.
如何验证勾股定理呢?
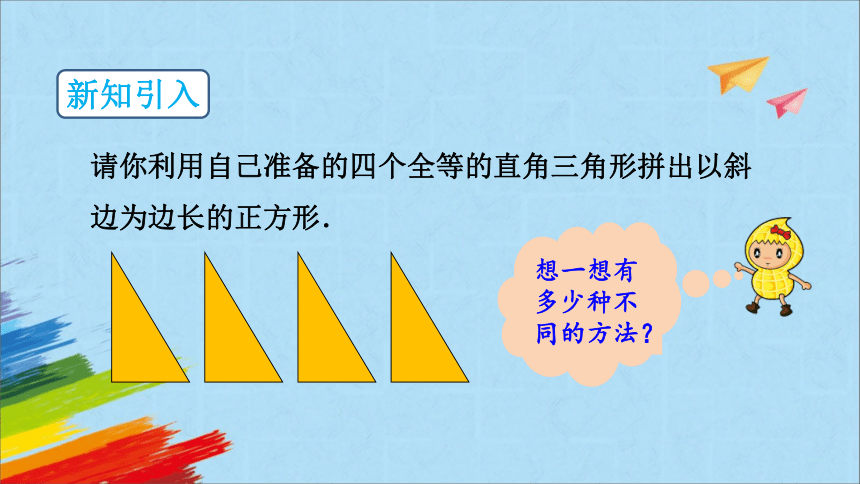
请你利用自己准备的四个全等的直角三角形拼出以斜边为边长的正方形.
新知引入
想一想有多少种不同的方法?
验证方法一
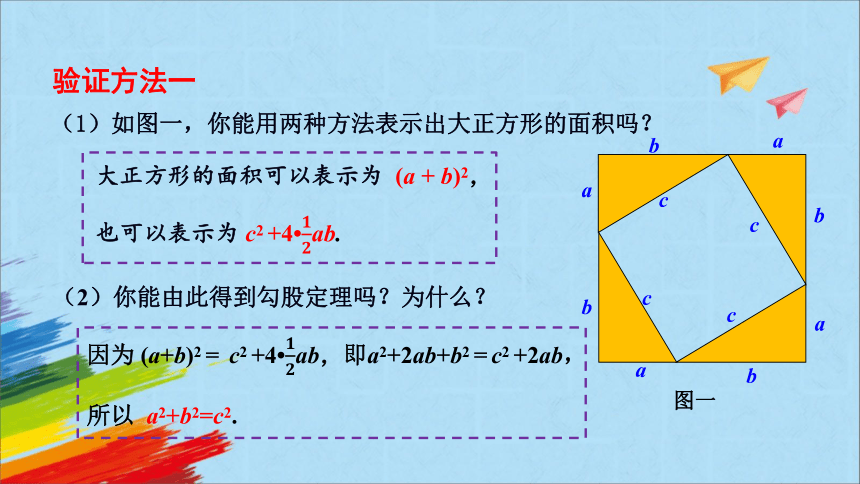
(1)如图一,你能用两种方法表示出大正方形的面积吗?
大正方形的面积可以表示为 (a + b)2,
也可以表示为 c2 +4 ab.
(2)你能由此得到勾股定理吗?为什么?
因为 (a+b)2 = c2 +4 ab,即a2+2ab+b2 = c2 +2ab,
所以 a2+b2=c2.
c
a
c
a
b
a
c
a
b
b
b
图一
c
验证方法二
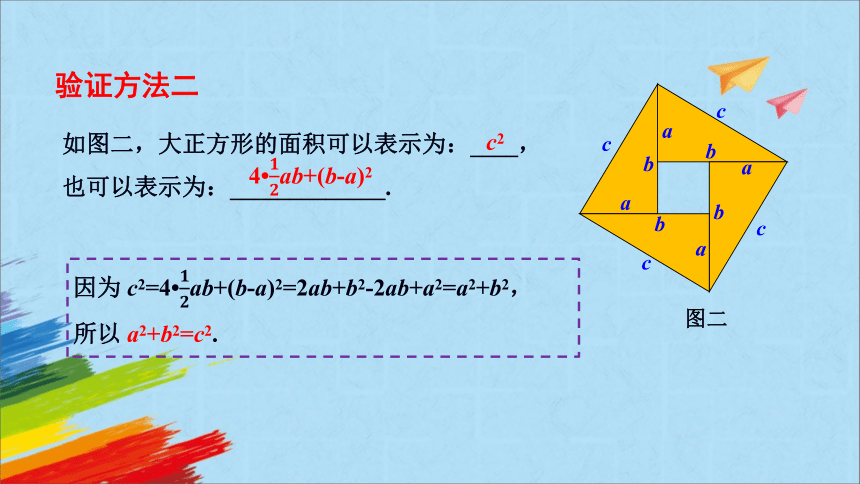
如图二,大正方形的面积可以表示为:____,
也可以表示为:_____________.
因为 c2=4 ab+(b-a)2=2ab+b2-2ab+a2=a2+b2,所以 a2+b2=c2.
c
a
c
a
b
c
a
b
b
b
a
c
图二
c2
4 ab+(b-a)2
总结:我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
想一想还有其他的方法吗?
c
a
c
a
b
c
a
b
b
b
a
c
图二
c
a
c
a
b
a
c
a
b
b
b
图一
c
验证方法三
b
c
a
b
c
a
A
B
C
D
利用小三角形面积之和等于大梯形面积的思路进行验证.
梯形面积:(a+b)×(a+b),
三角形面积之和:ab+ab+c2.
因为(a+b)×(a+b)=ab +ab+c2,
即(a2+2ab+b2)=ab+ab+c2,
所以 a2+b2=c2.
b
c
a
b
c
a
A
B
C
D
观察下图,判断图中三角形的三边长是否满足a2+b2=c2.
小试身手
不满足
不满足
我方侦查员小王在距离东西向公路400 m处侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400 m,10 s后,汽车与他相距500 m,你能帮小王计算敌方汽车的速度吗
例
题
公路
400 m
500 m
A
B
C
解:由勾股定理,可以得到AB2=BC2+AC2,
也就是5002=BC2+4002,所以BC=300.
敌方汽车10 s行驶了300 m,
那么它1 h行驶的距离为
300×6×60=108000(m)=108(km),
即它行驶的速度为108 km/h.
公路
400 m
500 m
A
B
C
1.飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4 km处,过了15 s,飞机距离这个男孩头顶5 km.这一过程中飞机飞过的距离是多少千米?
4 km
5 km
学以致用
解:在Rt△ABC中,
由勾股定理,得:
=-,
即=-=9,
则BC=3.
所以飞机飞过的距离是3 km.
C
B
A
2.如图,一根旗杆在离地面9 m处折断,旗杆顶部落在离旗杆底部12 m处.旗杆原来有多高
12 m
9 m
解:设旗杆顶部到折断处的距离为x m,
由勾股定理,得+=,
解得x=15,
所以15+9=24(m).
即旗杆原来高24 m.
课堂小结
(2)拼梯形图:
勾股定理的验证方法(数形结合法)
(1)拼正方形图:
勾股定理的应用
运用梯形面积表达式进行证明.
运用正方形面积表达式进行证明;
谢谢
第一章 勾股定理
1.1 探索勾股定理
第2课时 勾股定理的验证
1.经历验证勾股定理的过程,进一步发展空间观念和推理能力;
2.掌握勾股定理,并能运用勾股定理解决一些实际问题.
学习目标
回顾复习
勾股定理的内容是什么?
直角三角形两直角边的平方和等于斜边的平方.如果用a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
上节课我们仅仅是通过对具体的直角三角形数格子探索发现了勾股定理.
提出问题
事实上,现在已经有几百种勾股定理的验证方法,这节课我们也将要验证勾股定理.
对任意的直角三角形,勾股定理是否成立呢?这需要进一步验证.
如何验证勾股定理呢?
请你利用自己准备的四个全等的直角三角形拼出以斜边为边长的正方形.
新知引入
想一想有多少种不同的方法?
验证方法一
(1)如图一,你能用两种方法表示出大正方形的面积吗?
大正方形的面积可以表示为 (a + b)2,
也可以表示为 c2 +4 ab.
(2)你能由此得到勾股定理吗?为什么?
因为 (a+b)2 = c2 +4 ab,即a2+2ab+b2 = c2 +2ab,
所以 a2+b2=c2.
c
a
c
a
b
a
c
a
b
b
b
图一
c
验证方法二
如图二,大正方形的面积可以表示为:____,
也可以表示为:_____________.
因为 c2=4 ab+(b-a)2=2ab+b2-2ab+a2=a2+b2,所以 a2+b2=c2.
c
a
c
a
b
c
a
b
b
b
a
c
图二
c2
4 ab+(b-a)2
总结:我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
想一想还有其他的方法吗?
c
a
c
a
b
c
a
b
b
b
a
c
图二
c
a
c
a
b
a
c
a
b
b
b
图一
c
验证方法三
b
c
a
b
c
a
A
B
C
D
利用小三角形面积之和等于大梯形面积的思路进行验证.
梯形面积:(a+b)×(a+b),
三角形面积之和:ab+ab+c2.
因为(a+b)×(a+b)=ab +ab+c2,
即(a2+2ab+b2)=ab+ab+c2,
所以 a2+b2=c2.
b
c
a
b
c
a
A
B
C
D
观察下图,判断图中三角形的三边长是否满足a2+b2=c2.
小试身手
不满足
不满足
我方侦查员小王在距离东西向公路400 m处侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400 m,10 s后,汽车与他相距500 m,你能帮小王计算敌方汽车的速度吗
例
题
公路
400 m
500 m
A
B
C
解:由勾股定理,可以得到AB2=BC2+AC2,
也就是5002=BC2+4002,所以BC=300.
敌方汽车10 s行驶了300 m,
那么它1 h行驶的距离为
300×6×60=108000(m)=108(km),
即它行驶的速度为108 km/h.
公路
400 m
500 m
A
B
C
1.飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4 km处,过了15 s,飞机距离这个男孩头顶5 km.这一过程中飞机飞过的距离是多少千米?
4 km
5 km
学以致用
解:在Rt△ABC中,
由勾股定理,得:
=-,
即=-=9,
则BC=3.
所以飞机飞过的距离是3 km.
C
B
A
2.如图,一根旗杆在离地面9 m处折断,旗杆顶部落在离旗杆底部12 m处.旗杆原来有多高
12 m
9 m
解:设旗杆顶部到折断处的距离为x m,
由勾股定理,得+=,
解得x=15,
所以15+9=24(m).
即旗杆原来高24 m.
课堂小结
(2)拼梯形图:
勾股定理的验证方法(数形结合法)
(1)拼正方形图:
勾股定理的应用
运用梯形面积表达式进行证明.
运用正方形面积表达式进行证明;
谢谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
