北师大版八年级数学上册《2.7.2二次根式的乘除法和加减》教学课件(共18张PPT)
文档属性
| 名称 | 北师大版八年级数学上册《2.7.2二次根式的乘除法和加减》教学课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 979.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 12:48:15 | ||
图片预览





文档简介
(共18张PPT)
第二章 实数
2.7 二次根式
第2课时 二次根式的乘除法和加减
学习目标
能说出二次根式的运算法则,能运用法则进行二次根式(根号下仅限于数)的简单的四则运算,并解决简单的实际问题
构建动场
活动1:回顾二次根式的性质(两个公式):
,
(a≥0, b≥0)
(a≥0, b>0)
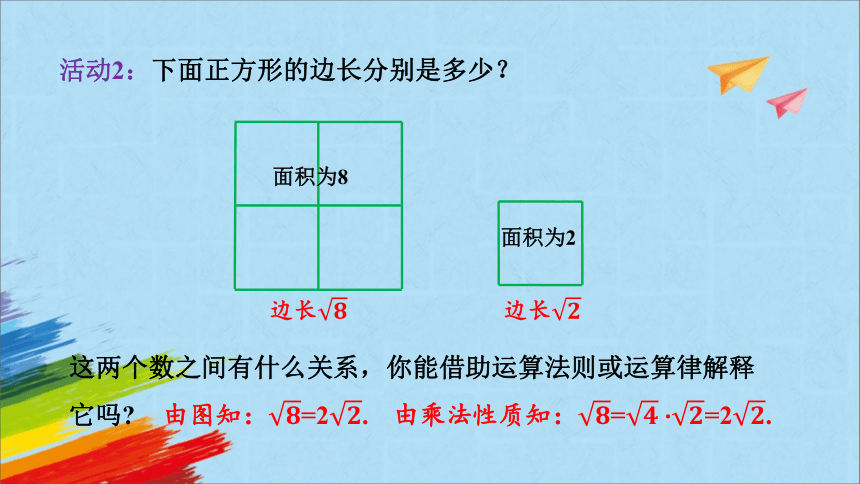
活动2:下面正方形的边长分别是多少?
面积为8
面积为2
边长
边长
这两个数之间有什么关系,你能借助运算法则或运算律解释
它吗
由图知:=2.
由乘法性质知:= ·=2.
自主学习
1.二次根式的乘法法则和除法法则
=______ (a≥0, b≥0),=______(a≥0, b>0).
对于二次根式的性质公式,将它们等号的左边与右边分别对换即可得:
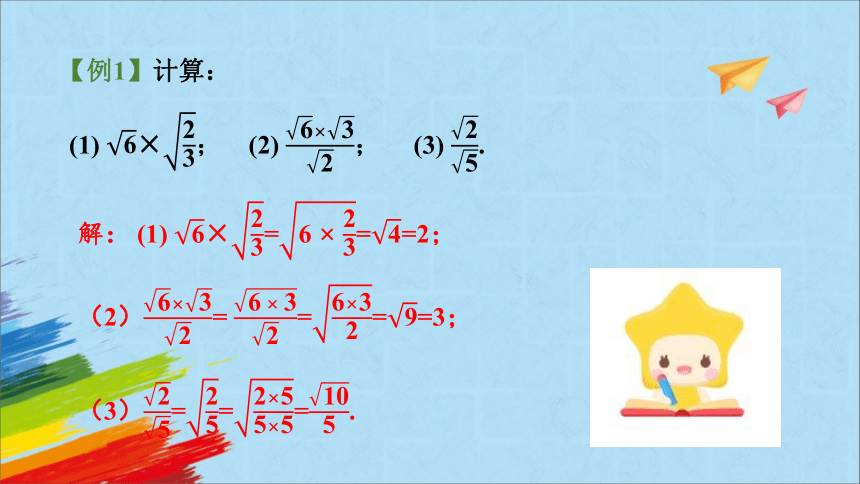
【例1】计算:
(1) ; (2) ; (3) .
解: (1) ===2;
(2)= ===3;
(3)===.
【例2】计算:
(1) ; (2)-5; (3) (+1)2 ;
解:(1)=3×2×=6;
(2)-5=-5=-5=6-5=1;
(3) (+1)2 =()2+2+1=5+2+1=6+2;
【例2】计算:
(4) (+3)×(3); (5) (- )×.
解: (4) (+3)×(3)=()2-32 =13-9=4;
(5) (-)×=×-=6-1=5.
注:二次根式也可以进行加减乘除运算,以前学习的实数的运算法则与运算律仍然适用.
合作探究
2.同类二次根式
定义:像4,6,这样几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式叫做同类二次根式.
注意:与化简后根号外的因数无关,与被开方数有关.
1.请你列举几个同类二次根式
,3,11,;
2.计算:
4+6=______; 4+ =______; 4-6=______;
-4+6=______; 4- =_____.
10
-2
2
注意:合并同类二次根式,系数相加,根式不变.
【例3】计算:
(1) + ; (2) -; (3)-.
解:(1)+=+ =3-2+=;
(2) -= -=-=;
(3) -=+-3=-+.
综合建模
1.二次根式的乘法法则和除法法则:
_____________________________________________.
= (a≥0, b≥0),= (a≥0, b>0)
2.二次根式化成最简二次根式后,如果__________相同,这几个二次根式叫做同类二次根式.
被开方数
3.合并同类二次根式,系数______,根式______.
相加
不变
当堂检测
1.计算: (1) ; (2) (2-1)2 ; (3) ()× ;
解:(1) = ==;
(2) (2-1)2= (2)2-4+1=13-4;
(3) ()×=×+×=+=2+3=5;
1.计算: (4) (1+)(2-);(5) ;(6) (43)÷2 .
解:(4)(1+)(2-)=2-+2-3=-1;
(5) - =-=3-2=1;
(6) (43)÷2= 4÷-÷=2-.
2.计算:
(1) ; (2) ; (3) + .
解: (1) =-=4-=3;
(2) ===;
(3) =+=+8.
3. (1)两个有理数相加、相减、相乘、相除,结果一定还是有理数吗 说明理由.
(2)两个无理数相加、相减、相乘、相除,结果一定还是无理数吗 说明理由.
解:(1)一定是,理由:两个有理数(整数或分数)相加、相减、相乘、相除,结果是整数或分数,仍是有理数;
(2)不一定是,反例:-+=0,·(-)=-3, =-1.
4.如图所示,图中小正方形的边长为1.
(1)试求图中梯形ABCD的面积.你有哪些方法
(2)试求图中梯形ABCD的周长
解:(1)方法一:如图, 根据梯形所在的长方形的面积减去四周三个直角三角形的面积, 得
梯形ABCD的面积
=7×5-×2×4-×1×1-×5×5
=18;
解:(1)方法二:如图,把梯形分成一个小梯形和2个三角形,得
梯形ABCD的面积
=×3×1+×(3+5)+×5×5
=18;
(2)梯形ABCD的周长
=+ + +6
=6+2 +6.
第二章 实数
2.7 二次根式
第2课时 二次根式的乘除法和加减
学习目标
能说出二次根式的运算法则,能运用法则进行二次根式(根号下仅限于数)的简单的四则运算,并解决简单的实际问题
构建动场
活动1:回顾二次根式的性质(两个公式):
,
(a≥0, b≥0)
(a≥0, b>0)
活动2:下面正方形的边长分别是多少?
面积为8
面积为2
边长
边长
这两个数之间有什么关系,你能借助运算法则或运算律解释
它吗
由图知:=2.
由乘法性质知:= ·=2.
自主学习
1.二次根式的乘法法则和除法法则
=______ (a≥0, b≥0),=______(a≥0, b>0).
对于二次根式的性质公式,将它们等号的左边与右边分别对换即可得:
【例1】计算:
(1) ; (2) ; (3) .
解: (1) ===2;
(2)= ===3;
(3)===.
【例2】计算:
(1) ; (2)-5; (3) (+1)2 ;
解:(1)=3×2×=6;
(2)-5=-5=-5=6-5=1;
(3) (+1)2 =()2+2+1=5+2+1=6+2;
【例2】计算:
(4) (+3)×(3); (5) (- )×.
解: (4) (+3)×(3)=()2-32 =13-9=4;
(5) (-)×=×-=6-1=5.
注:二次根式也可以进行加减乘除运算,以前学习的实数的运算法则与运算律仍然适用.
合作探究
2.同类二次根式
定义:像4,6,这样几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式叫做同类二次根式.
注意:与化简后根号外的因数无关,与被开方数有关.
1.请你列举几个同类二次根式
,3,11,;
2.计算:
4+6=______; 4+ =______; 4-6=______;
-4+6=______; 4- =_____.
10
-2
2
注意:合并同类二次根式,系数相加,根式不变.
【例3】计算:
(1) + ; (2) -; (3)-.
解:(1)+=+ =3-2+=;
(2) -= -=-=;
(3) -=+-3=-+.
综合建模
1.二次根式的乘法法则和除法法则:
_____________________________________________.
= (a≥0, b≥0),= (a≥0, b>0)
2.二次根式化成最简二次根式后,如果__________相同,这几个二次根式叫做同类二次根式.
被开方数
3.合并同类二次根式,系数______,根式______.
相加
不变
当堂检测
1.计算: (1) ; (2) (2-1)2 ; (3) ()× ;
解:(1) = ==;
(2) (2-1)2= (2)2-4+1=13-4;
(3) ()×=×+×=+=2+3=5;
1.计算: (4) (1+)(2-);(5) ;(6) (43)÷2 .
解:(4)(1+)(2-)=2-+2-3=-1;
(5) - =-=3-2=1;
(6) (43)÷2= 4÷-÷=2-.
2.计算:
(1) ; (2) ; (3) + .
解: (1) =-=4-=3;
(2) ===;
(3) =+=+8.
3. (1)两个有理数相加、相减、相乘、相除,结果一定还是有理数吗 说明理由.
(2)两个无理数相加、相减、相乘、相除,结果一定还是无理数吗 说明理由.
解:(1)一定是,理由:两个有理数(整数或分数)相加、相减、相乘、相除,结果是整数或分数,仍是有理数;
(2)不一定是,反例:-+=0,·(-)=-3, =-1.
4.如图所示,图中小正方形的边长为1.
(1)试求图中梯形ABCD的面积.你有哪些方法
(2)试求图中梯形ABCD的周长
解:(1)方法一:如图, 根据梯形所在的长方形的面积减去四周三个直角三角形的面积, 得
梯形ABCD的面积
=7×5-×2×4-×1×1-×5×5
=18;
解:(1)方法二:如图,把梯形分成一个小梯形和2个三角形,得
梯形ABCD的面积
=×3×1+×(3+5)+×5×5
=18;
(2)梯形ABCD的周长
=+ + +6
=6+2 +6.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
