人教版六年级下册3.1.7 解决问题—等积法(课件)(共16张PPT)
文档属性
| 名称 | 人教版六年级下册3.1.7 解决问题—等积法(课件)(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 13:12:35 | ||
图片预览

文档简介
(共16张PPT)
3.1.7 解决问题
——等体积法
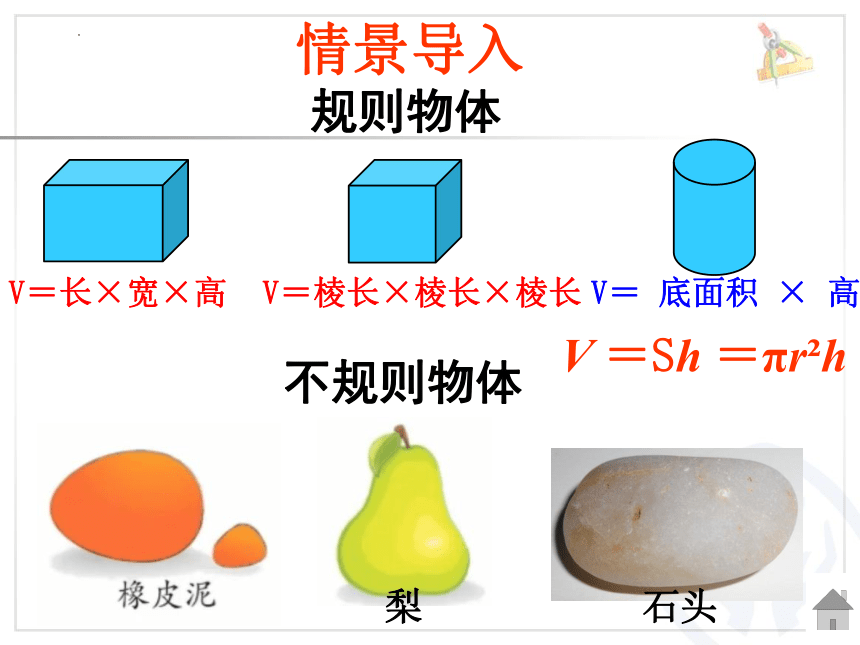
规则物体
不规则物体
情景导入
V=长×宽×高
V=棱长×棱长×棱长
V= 底面积 × 高
V =Sh =πr h
梨
石头
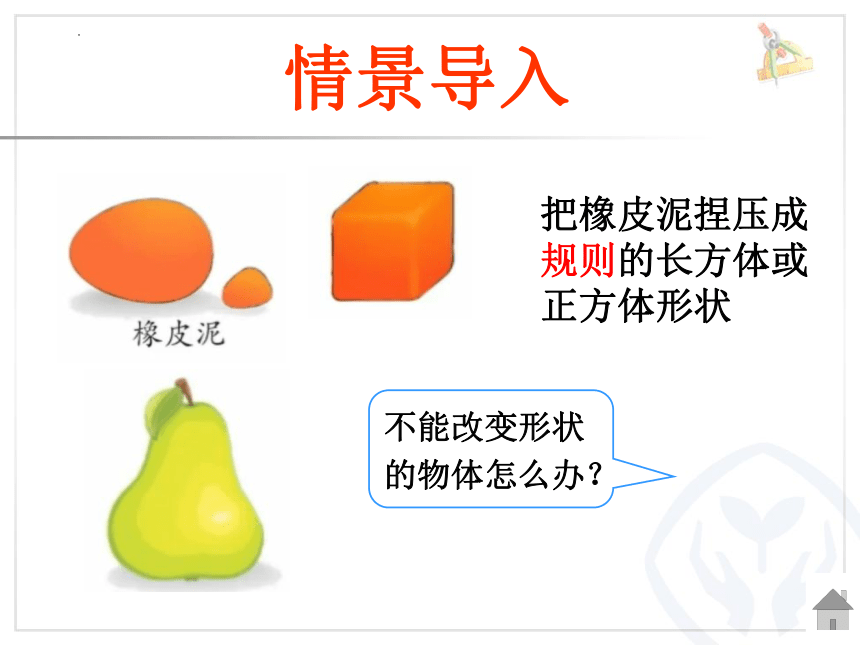
把橡皮泥捏压成规则的长方体或正方体形状
不能改变形状的物体怎么办?
情景导入
情景导入
情景导入
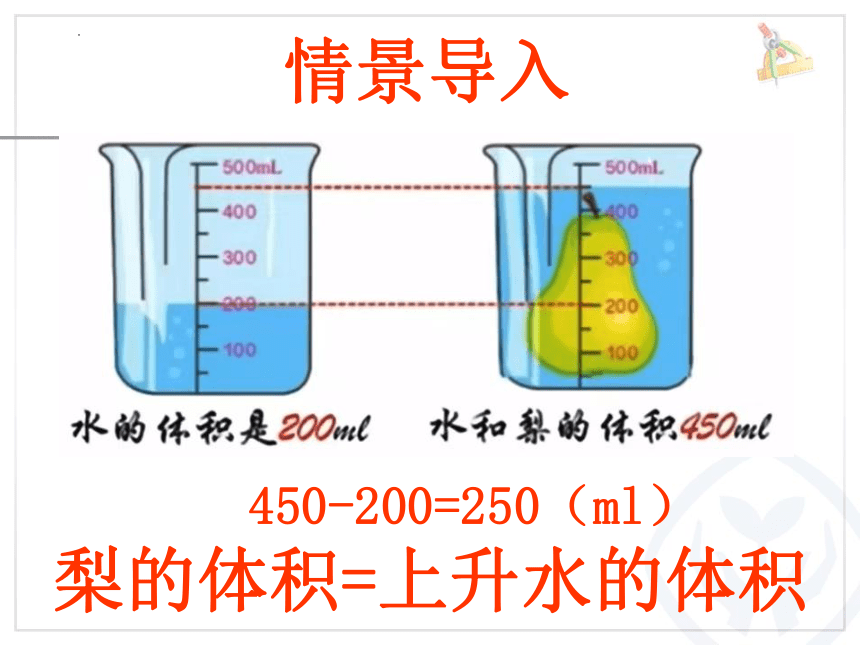
450-200=250(ml)
梨的体积=上升水的体积
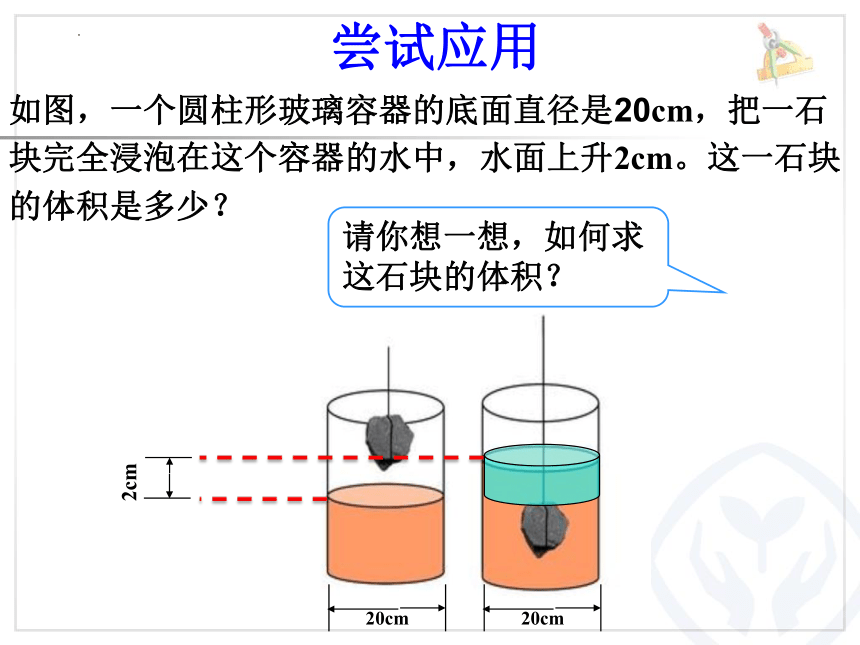
如图,一个圆柱形玻璃容器的底面直径是20cm,把一石块完全浸泡在这个容器的水中,水面上升2cm。这一石块的体积是多少?
请你想一想,如何求这石块的体积?
尝试应用
2cm
20cm
20cm
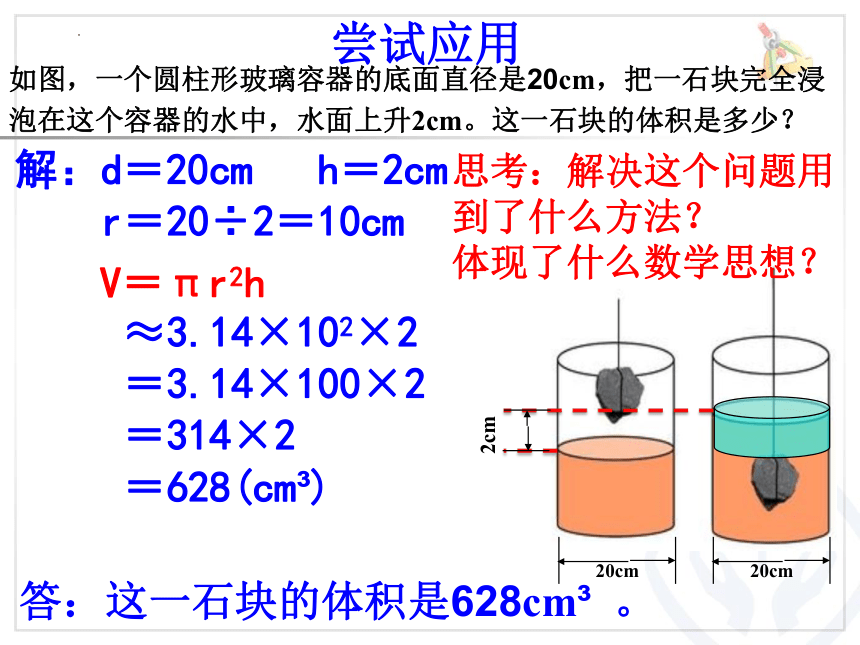
解:d=20cm h=2cm
r=20÷2=10cm
答:这一石块的体积是628cm 。
V=πr2h
≈3.14×102×2
=3.14×100×2
=314×2
=628(cm )
尝试应用
如图,一个圆柱形玻璃容器的底面直径是20cm,把一石块完全浸泡在这个容器的水中,水面上升2cm。这一石块的体积是多少?
2cm
20cm
20cm
思考:解决这个问题用到了什么方法?
体现了什么数学思想?
7cm
请你仔细想一想,怎么能计算出瓶子的容积呢?
一个内直径是8cm的瓶子里,喝过之后剩余水的高度是7cm。这个瓶子的容积是多少?
再攀高峰
18cm
把瓶盖拧紧倒置放平,无水部分是圆柱形,
高度是18cm。
8cm
通过观察瓶子的倒置,你们有什么发现呢?
351.68+904.32=1256cm3= 1256mL
答:这个瓶子的容积是1256mL。
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
解:d=8cm h水=7cm h空=18cm
r=8÷2=4cm
V水=πr2h水
≈3.14×42×7
=351.68(cm )
V空=πr2h空
≈3.14×42×18
=904.32(cm )
答:这个瓶子的容积是1256mL。
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
解:d=8cm h水=7cm h空=18cm
r=8÷2=4cm
V=πr2(h水 +h空 )
≈3.14×42×(7+18)
=1256(cm )
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
我们利用了体积不变的特性,把不规则图形转化成规则图形来计算。
1.一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内直径是6cm。小明喝了多少水?
10cm
无水部分高为10cm圆柱的体积就是小明喝了的水的体积。
请你仔细想一想,小明喝了的水的体积该怎么计算呢?
补偿练习
1.一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
答:小明喝了282.6mL的水。
10cm
解:d=6cm h=10cm
r=6÷2=3cm
V=πr2h
≈3.14×32×10
=3.14×9×10
=282.6(cm )
=282.6(mL)
2.学校要在教学区和操场之间修一道围墙,原计划用土石35m 。后来多开了一个厚度为25cm的月亮门,减少了土石的用量。现在用了多少立方米的土石?
补偿练习
计划用土减去挖空部分高为25cm,半径为1m的圆柱的体积就是实际用土的体积。
请你仔细想一想,要想知道现在用多少立方米的土石?就要先求什么?
2.学校要在教学区和操场之间修一道围墙,原计划用土石35m 。后来多开了一个厚度为25cm的月亮门,减少了土石的用量。现在用了多少立方米的土石?
答:现在用了34.215立方米的土石。
补偿练习
35-0.785=34.215(m )
解:d=2m h=25cm=0.25m
r=2÷2=1m
V=πr2h
≈3.14×12×0.25
=0.785(m )
通过本节课的学习,你有哪些收获?
小 结
日
转化
思想
知识
知
方法
等体积法
3.1.7 解决问题
——等体积法
规则物体
不规则物体
情景导入
V=长×宽×高
V=棱长×棱长×棱长
V= 底面积 × 高
V =Sh =πr h
梨
石头
把橡皮泥捏压成规则的长方体或正方体形状
不能改变形状的物体怎么办?
情景导入
情景导入
情景导入
450-200=250(ml)
梨的体积=上升水的体积
如图,一个圆柱形玻璃容器的底面直径是20cm,把一石块完全浸泡在这个容器的水中,水面上升2cm。这一石块的体积是多少?
请你想一想,如何求这石块的体积?
尝试应用
2cm
20cm
20cm
解:d=20cm h=2cm
r=20÷2=10cm
答:这一石块的体积是628cm 。
V=πr2h
≈3.14×102×2
=3.14×100×2
=314×2
=628(cm )
尝试应用
如图,一个圆柱形玻璃容器的底面直径是20cm,把一石块完全浸泡在这个容器的水中,水面上升2cm。这一石块的体积是多少?
2cm
20cm
20cm
思考:解决这个问题用到了什么方法?
体现了什么数学思想?
7cm
请你仔细想一想,怎么能计算出瓶子的容积呢?
一个内直径是8cm的瓶子里,喝过之后剩余水的高度是7cm。这个瓶子的容积是多少?
再攀高峰
18cm
把瓶盖拧紧倒置放平,无水部分是圆柱形,
高度是18cm。
8cm
通过观察瓶子的倒置,你们有什么发现呢?
351.68+904.32=1256cm3= 1256mL
答:这个瓶子的容积是1256mL。
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
解:d=8cm h水=7cm h空=18cm
r=8÷2=4cm
V水=πr2h水
≈3.14×42×7
=351.68(cm )
V空=πr2h空
≈3.14×42×18
=904.32(cm )
答:这个瓶子的容积是1256mL。
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
解:d=8cm h水=7cm h空=18cm
r=8÷2=4cm
V=πr2(h水 +h空 )
≈3.14×42×(7+18)
=1256(cm )
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
我们利用了体积不变的特性,把不规则图形转化成规则图形来计算。
1.一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内直径是6cm。小明喝了多少水?
10cm
无水部分高为10cm圆柱的体积就是小明喝了的水的体积。
请你仔细想一想,小明喝了的水的体积该怎么计算呢?
补偿练习
1.一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
答:小明喝了282.6mL的水。
10cm
解:d=6cm h=10cm
r=6÷2=3cm
V=πr2h
≈3.14×32×10
=3.14×9×10
=282.6(cm )
=282.6(mL)
2.学校要在教学区和操场之间修一道围墙,原计划用土石35m 。后来多开了一个厚度为25cm的月亮门,减少了土石的用量。现在用了多少立方米的土石?
补偿练习
计划用土减去挖空部分高为25cm,半径为1m的圆柱的体积就是实际用土的体积。
请你仔细想一想,要想知道现在用多少立方米的土石?就要先求什么?
2.学校要在教学区和操场之间修一道围墙,原计划用土石35m 。后来多开了一个厚度为25cm的月亮门,减少了土石的用量。现在用了多少立方米的土石?
答:现在用了34.215立方米的土石。
补偿练习
35-0.785=34.215(m )
解:d=2m h=25cm=0.25m
r=2÷2=1m
V=πr2h
≈3.14×12×0.25
=0.785(m )
通过本节课的学习,你有哪些收获?
小 结
日
转化
思想
知识
知
方法
等体积法
