4.3.2.1 角的比较 课件(共35张PPT)
文档属性
| 名称 | 4.3.2.1 角的比较 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 20:06:20 | ||
图片预览









文档简介
(共35张PPT)
角
(第二课时)
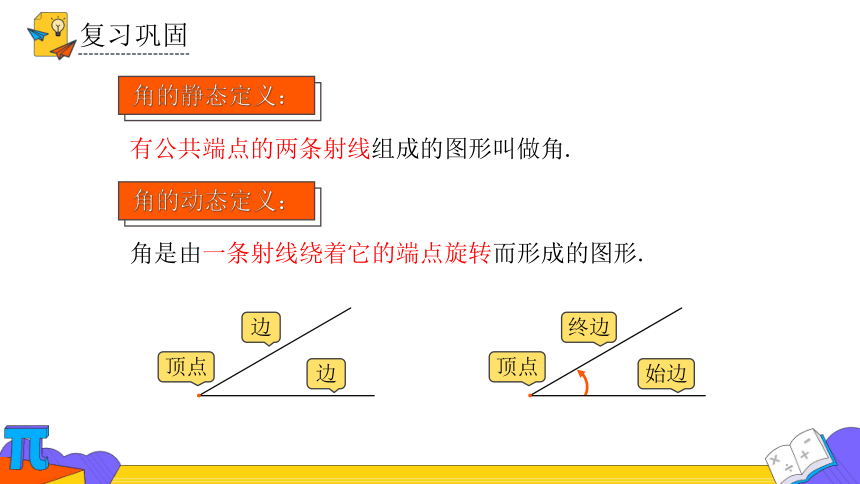
角的动态定义:
复习巩固
有公共端点的两条射线组成的图形叫做角.
角是由一条射线绕着它的端点旋转而形成的图形.
顶点
边
边
顶点
终边
始边
角的静态定义:
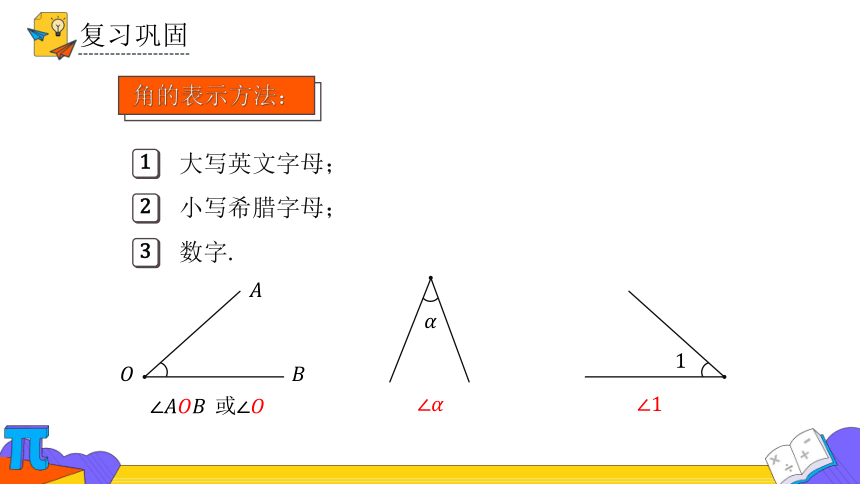
大写英文字母;
小写希腊字母;
数字.
1
2
3
或
角的表示方法:
复习巩固
周角 ,
平角 ,
,
.
角的换算:
1
2
3
4
复习巩固
度分秒的求和运算与第一章学习的有理数的求和运算,有什么相同点和不同点吗?
思考
度分秒之间同单位的换算是十进制的;
度分秒之间的相互转换是六十进制的.
例题讲解
;
1
同单位直接相加
;
每满 进
计算:
例1
例题讲解
;
2
解:
借 作
;
同单位直接相减
计算:
例1
与加法类似,先进行同单位的运算.
分析
借 作
例题讲解
;
3
解:
化为和
满 进
;
乘法分配律
计算:
例1
例题讲解
(精确到分)
4
解:
.
精确到分,要先取到小数点后 位,
计算:
例1
然后再四舍五入.
法
先把 约等于多少度算出来,再把度化成分.
分析
(精确到分)
4
.
例题讲解
四舍五入,精确到分.
计算:
例1
法
后还需要有一位小数,因此此处要先保留两位小数.
分析
解:
小结
先把度、分、秒分别求和或作差;
然后根据满 进 ,或借 作 ,计算得到最后的结果.
1
2
先把度、分、秒同时乘以倍数或除以份数;
再根据题目的要求,计算得到最后的结果.
1
2
和差运算:
倍分运算:
学习新知
角的大小比较和角的运算.
线段的定义和表示方法
线段的长短比较和线段的运算
根据学习线段的经验,接下来将要学习角的什么内容?
思考
学习新知
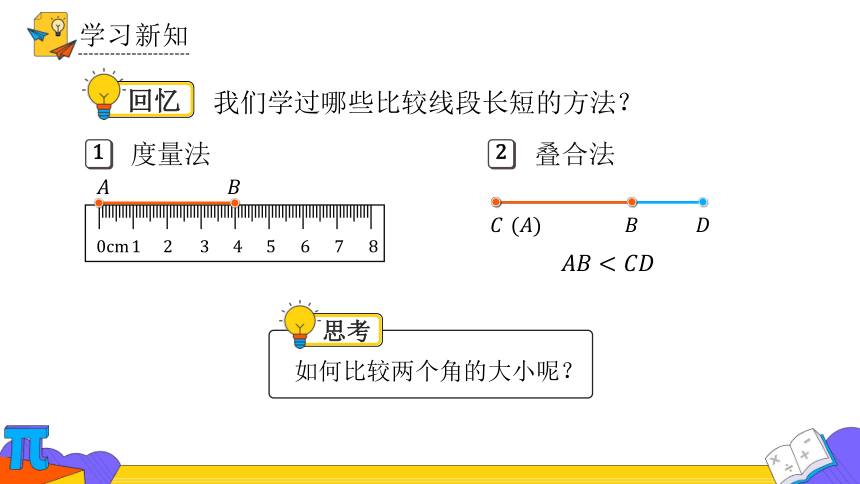
我们学过哪些比较线段长短的方法?
度量法
1
2
叠合法
回忆
如何比较两个角的大小呢?
思考
方法 (度量法)
学习新知
角的大小比较
如何比较 与 的大小呢?
用量角器量出 与 的度数,
就可以比较它们的大小了.
图中,
所以 .
,
学习新知
角的大小比较
还有什么方法比较 与 的大小呢?
将两个角的一边重合在一起,两个角的另一边落在第一边的同一侧,观察这两边的位置,就可以确定两个角的大小了.
方法 (叠合法)
学习新知
角的大小比较
固定 的位置,
与 在 的同一侧,
若 在 内部,则 ;
若 与 重合,则 ;
若 在 外部,则 ;
让 的边 与 重合,
学习新知
两个角的三种大小关系:小于,等于或大于.
角的大小比较
学习新知
度量法
判断下图中 与 的大小关系.
角的大小与角的两边张开的大小有关;与角的边画出的长短无关.
注意
学习新知
叠合法
判断下图中 与 的大小关系.
例题讲解
;
1
;
2
;
3
.
4
如图,用“、 或 ”填空.
例2
学习新知
图中有 和 ,
共 个角.
能用等式表示它们之间满足的数量关系吗?
思考
图中共有几个角?
观察
学习新知
角的和差
是 与 的和,
记作 ;
是 与 的差,
记作 ;
类似地, .
例题讲解
;
1
;
2
如图,填空:
例3
例题讲解
;
3
如图,填空:
例3
例题讲解
.
4
如图,填空:
例3
例题讲解
1
例4
一副三角尺中包含哪些度数的角?
一副三角尺中含有 的角.
用一个三角尺能画出的角.
例题讲解
2
例4
一副三角尺可以画出哪些大于 度小于 度的角?
这些角有什么共同点?
用一副三角尺可以拼出这些图形
例题讲解
用一副三角尺可以拼出这些图形
2
例4
一副三角尺可以画出哪些大于 度小于 度的角?
这些角有什么共同点?
例题讲解
用一副三角尺可以拼出这些图形
2
例4
一副三角尺可以画出哪些大于 度小于 度的角?
这些角有什么共同点?
例题讲解
用一副三角尺可以拼出这些图形
2
例4
一副三角尺可以画出哪些大于 度小于 度的角?
这些角有什么共同点?
这些角的度数都是 的倍数.
例题讲解
一副三角尺可以画出
.
2
例4
一副三角尺可以画出哪些大于 度小于 度的角?
这些角有什么共同点?
方法 (度量法)
用量角器量出 与 的度数,
就可以比较它们的大小了.
图中,
所以 .
,
角的大小比较
课
堂
小
结
角的大小比较
将两个角的一边重合在一起,两个角的另一边落在第一边的同一侧,观察这两边的位置,就可以确定两个角的大小了.
方法 (叠合法)
课
堂
小
结
两个角的和或差,仍然是一个角.
如图, 是 与 的和,
记作 ;
是 与 的差,
记作 ;
角的和或差
课
堂
小
结
在本节课内容的学习过程中,通过类比线段长短的比较,学习了角的大小比较,这体现了我们在数学学习中经常用到的类比的数学思想;在没有给定图形时,我们运用分类讨论的思想画出了题目所包含的全部图形.
数学思想方法:
课
堂
小
结
再 见
角
(第二课时)
角的动态定义:
复习巩固
有公共端点的两条射线组成的图形叫做角.
角是由一条射线绕着它的端点旋转而形成的图形.
顶点
边
边
顶点
终边
始边
角的静态定义:
大写英文字母;
小写希腊字母;
数字.
1
2
3
或
角的表示方法:
复习巩固
周角 ,
平角 ,
,
.
角的换算:
1
2
3
4
复习巩固
度分秒的求和运算与第一章学习的有理数的求和运算,有什么相同点和不同点吗?
思考
度分秒之间同单位的换算是十进制的;
度分秒之间的相互转换是六十进制的.
例题讲解
;
1
同单位直接相加
;
每满 进
计算:
例1
例题讲解
;
2
解:
借 作
;
同单位直接相减
计算:
例1
与加法类似,先进行同单位的运算.
分析
借 作
例题讲解
;
3
解:
化为和
满 进
;
乘法分配律
计算:
例1
例题讲解
(精确到分)
4
解:
.
精确到分,要先取到小数点后 位,
计算:
例1
然后再四舍五入.
法
先把 约等于多少度算出来,再把度化成分.
分析
(精确到分)
4
.
例题讲解
四舍五入,精确到分.
计算:
例1
法
后还需要有一位小数,因此此处要先保留两位小数.
分析
解:
小结
先把度、分、秒分别求和或作差;
然后根据满 进 ,或借 作 ,计算得到最后的结果.
1
2
先把度、分、秒同时乘以倍数或除以份数;
再根据题目的要求,计算得到最后的结果.
1
2
和差运算:
倍分运算:
学习新知
角的大小比较和角的运算.
线段的定义和表示方法
线段的长短比较和线段的运算
根据学习线段的经验,接下来将要学习角的什么内容?
思考
学习新知
我们学过哪些比较线段长短的方法?
度量法
1
2
叠合法
回忆
如何比较两个角的大小呢?
思考
方法 (度量法)
学习新知
角的大小比较
如何比较 与 的大小呢?
用量角器量出 与 的度数,
就可以比较它们的大小了.
图中,
所以 .
,
学习新知
角的大小比较
还有什么方法比较 与 的大小呢?
将两个角的一边重合在一起,两个角的另一边落在第一边的同一侧,观察这两边的位置,就可以确定两个角的大小了.
方法 (叠合法)
学习新知
角的大小比较
固定 的位置,
与 在 的同一侧,
若 在 内部,则 ;
若 与 重合,则 ;
若 在 外部,则 ;
让 的边 与 重合,
学习新知
两个角的三种大小关系:小于,等于或大于.
角的大小比较
学习新知
度量法
判断下图中 与 的大小关系.
角的大小与角的两边张开的大小有关;与角的边画出的长短无关.
注意
学习新知
叠合法
判断下图中 与 的大小关系.
例题讲解
;
1
;
2
;
3
.
4
如图,用“、 或 ”填空.
例2
学习新知
图中有 和 ,
共 个角.
能用等式表示它们之间满足的数量关系吗?
思考
图中共有几个角?
观察
学习新知
角的和差
是 与 的和,
记作 ;
是 与 的差,
记作 ;
类似地, .
例题讲解
;
1
;
2
如图,填空:
例3
例题讲解
;
3
如图,填空:
例3
例题讲解
.
4
如图,填空:
例3
例题讲解
1
例4
一副三角尺中包含哪些度数的角?
一副三角尺中含有 的角.
用一个三角尺能画出的角.
例题讲解
2
例4
一副三角尺可以画出哪些大于 度小于 度的角?
这些角有什么共同点?
用一副三角尺可以拼出这些图形
例题讲解
用一副三角尺可以拼出这些图形
2
例4
一副三角尺可以画出哪些大于 度小于 度的角?
这些角有什么共同点?
例题讲解
用一副三角尺可以拼出这些图形
2
例4
一副三角尺可以画出哪些大于 度小于 度的角?
这些角有什么共同点?
例题讲解
用一副三角尺可以拼出这些图形
2
例4
一副三角尺可以画出哪些大于 度小于 度的角?
这些角有什么共同点?
这些角的度数都是 的倍数.
例题讲解
一副三角尺可以画出
.
2
例4
一副三角尺可以画出哪些大于 度小于 度的角?
这些角有什么共同点?
方法 (度量法)
用量角器量出 与 的度数,
就可以比较它们的大小了.
图中,
所以 .
,
角的大小比较
课
堂
小
结
角的大小比较
将两个角的一边重合在一起,两个角的另一边落在第一边的同一侧,观察这两边的位置,就可以确定两个角的大小了.
方法 (叠合法)
课
堂
小
结
两个角的和或差,仍然是一个角.
如图, 是 与 的和,
记作 ;
是 与 的差,
记作 ;
角的和或差
课
堂
小
结
在本节课内容的学习过程中,通过类比线段长短的比较,学习了角的大小比较,这体现了我们在数学学习中经常用到的类比的数学思想;在没有给定图形时,我们运用分类讨论的思想画出了题目所包含的全部图形.
数学思想方法:
课
堂
小
结
再 见
