4.3.3.1 余角 课件(共23张PPT)
文档属性
| 名称 | 4.3.3.1 余角 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 20:05:28 | ||
图片预览


文档简介
(共23张PPT)
角
(第四课时)
引入新知
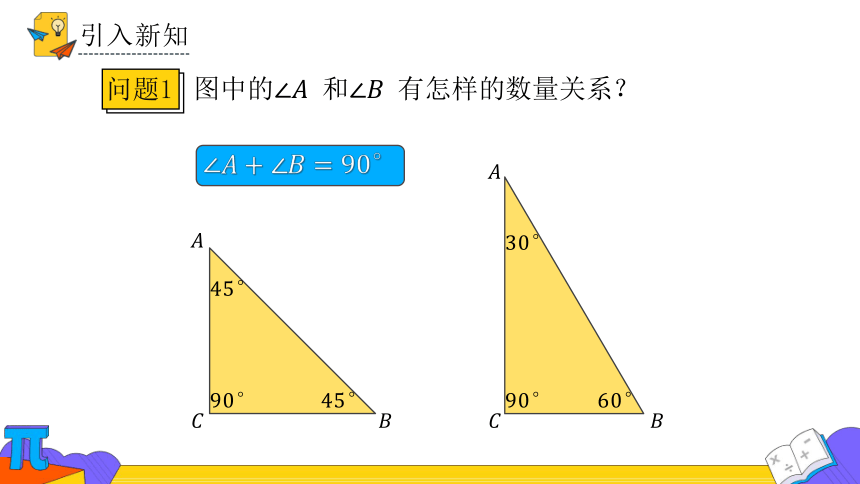
图中的 和 有怎样的数量关系?
问题1
引入新知
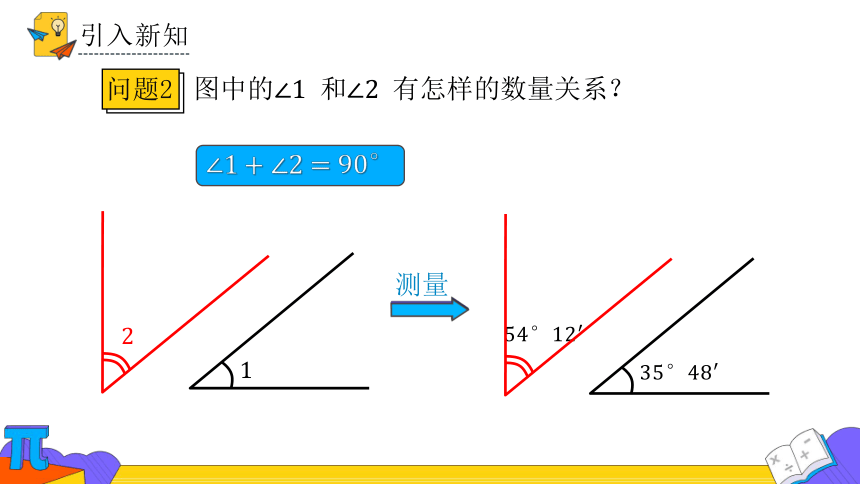
图中的 和 有怎样的数量关系?
问题2
测量
引入新知
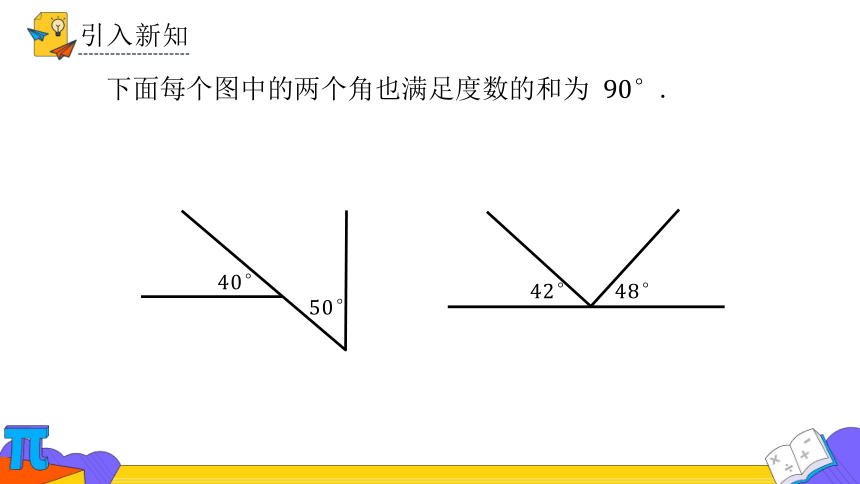
下面每个图中的两个角也满足度数的和为 .
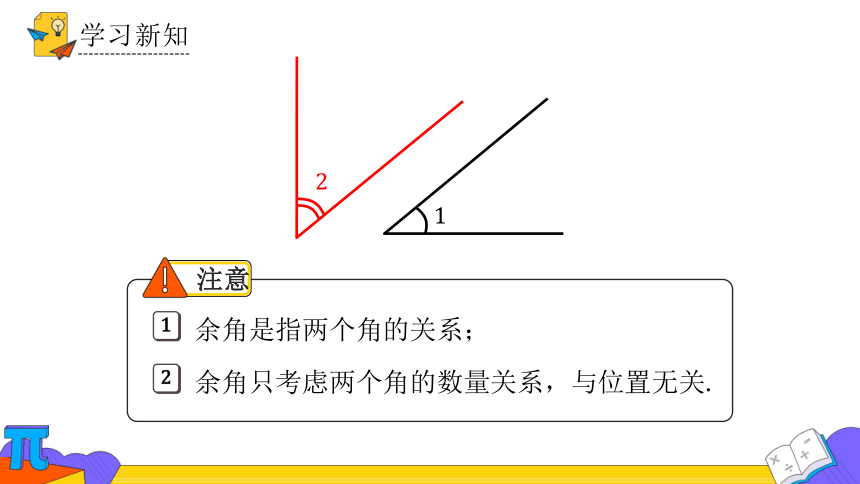
学习新知
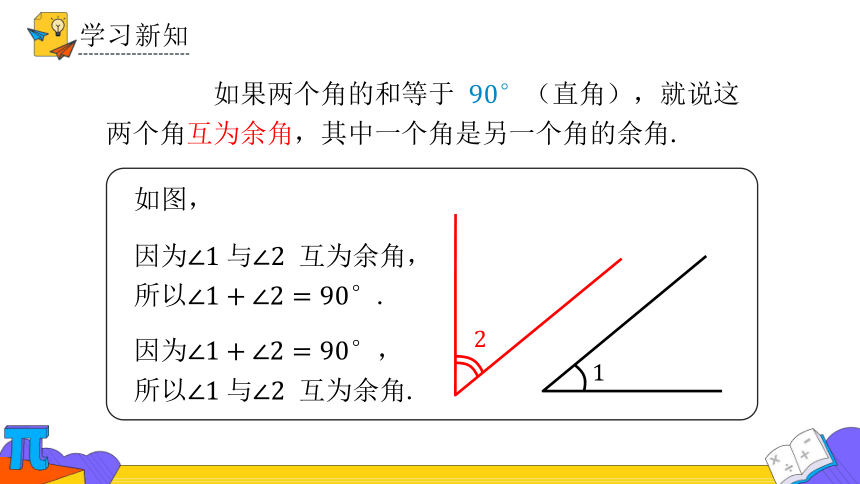
如果两个角的和等于 (直角),就说这两个角互为余角,其中一个角是另一个角的余角.
如图,
因为 互为余角,所以.
因为,
所以.
学习新知
余角是指两个角的关系;
余角只考虑两个角的数量关系,与位置无关.
注意
1
2
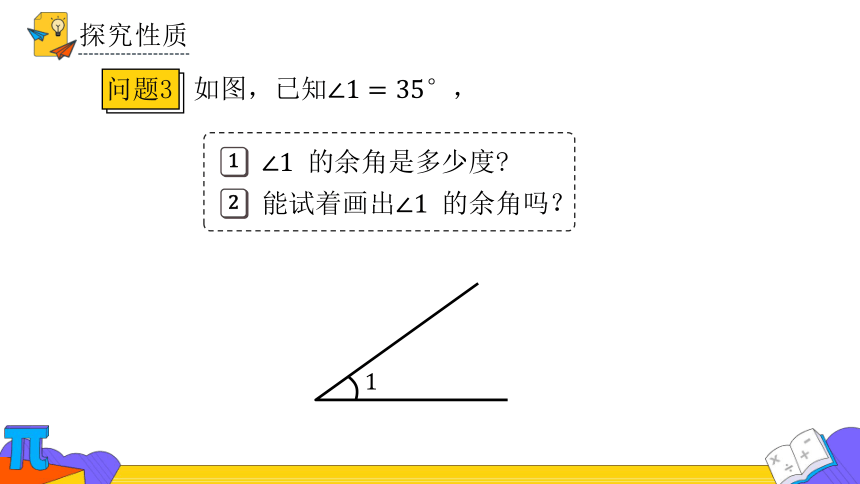
探究性质
如图,已知,
问题3
1
2
的余角是多少度
能试着画出 的余角吗?
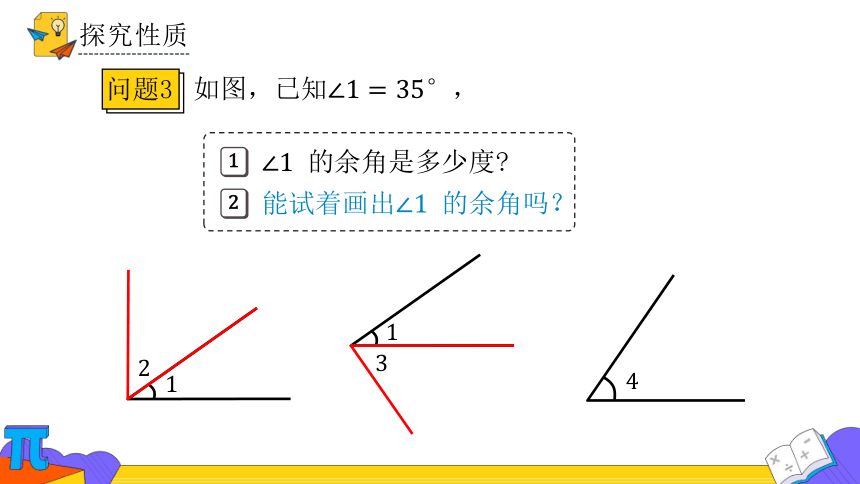
探究性质
如图,已知,
问题3
1
2
的余角是多少度
能试着画出 的余角吗?
探究性质
与 互为余角, 与 互为余角,那么 与 有怎样的数量关系呢?
思考
你能证明这个结论吗?
探究性质
与 互为余角, 与 互为余角,那么 与 有怎样的数量关系呢?
思考
已知: 与 互余, 与 互余,
由等式性质可得.
求证:.
证明:
所以.
同理,因为 与 互余,所以,
所以.
因为 与 互余,所以
探究性质
同角的余角相等.
因为 ,,
所以.
如果,,且,那么 吗?
问题
探究性质
等角的余角相等.
因为,,且,
所以.
同角(等角)的余角相等.
性质
应用新知
已知, 与 互为余角,求 的度数.
例1
因为 与 互为余角,
分析
所以根据余角的定义,可得
所以,
因为,所以可求出 的度数.
应用新知
已知, 与 互为余角,求 的度数.
例1
因为 与 互为余角(已知),
所以(余角定义),
所以.
因为,
解:
所以.
应用新知
一个角比它的余角大 ,求这个角的度数.
例2
设这个角为 .
分析
根据余角的定义,它的余角表示为,
题目中的数量关系:这个角它的余角.
应用新知
设这个角为 ,依题意得:
答:这个角为 .
解:
一个角比它的余角大 ,求这个角的度数.
例2
如图,点 ,, 在同一直线上,射线 和射线 分别平分 和,
例3
求 的度数;
;
.
分析
因为点,, 在同一直线上,
所以.
又因为射线 和射线 分别平分 和,
所以
解:
.
如图,点 ,, 在同一直线上,射线 和射线 分别平分 和,
例3
求 的度数;
所以.
;
解:
如图,点 ,, 在同一直线上,射线 和射线 分别平分 和,
例3
图中哪些角互为余角?
.
;
;
课
堂
小
结
因为 与 互为余角,
所以.
因为,
所以 与 互为余角.
.余角的概念
和为 的两个角互为余角.
课
堂
小
结
因为,
所以.
因为,,且,
所以.
.余角的性质
同角(等角)的余角相等.
课后作业
如图,三角形 中,,, ,求 的度数.
再 见
角
(第四课时)
引入新知
图中的 和 有怎样的数量关系?
问题1
引入新知
图中的 和 有怎样的数量关系?
问题2
测量
引入新知
下面每个图中的两个角也满足度数的和为 .
学习新知
如果两个角的和等于 (直角),就说这两个角互为余角,其中一个角是另一个角的余角.
如图,
因为 互为余角,所以.
因为,
所以.
学习新知
余角是指两个角的关系;
余角只考虑两个角的数量关系,与位置无关.
注意
1
2
探究性质
如图,已知,
问题3
1
2
的余角是多少度
能试着画出 的余角吗?
探究性质
如图,已知,
问题3
1
2
的余角是多少度
能试着画出 的余角吗?
探究性质
与 互为余角, 与 互为余角,那么 与 有怎样的数量关系呢?
思考
你能证明这个结论吗?
探究性质
与 互为余角, 与 互为余角,那么 与 有怎样的数量关系呢?
思考
已知: 与 互余, 与 互余,
由等式性质可得.
求证:.
证明:
所以.
同理,因为 与 互余,所以,
所以.
因为 与 互余,所以
探究性质
同角的余角相等.
因为 ,,
所以.
如果,,且,那么 吗?
问题
探究性质
等角的余角相等.
因为,,且,
所以.
同角(等角)的余角相等.
性质
应用新知
已知, 与 互为余角,求 的度数.
例1
因为 与 互为余角,
分析
所以根据余角的定义,可得
所以,
因为,所以可求出 的度数.
应用新知
已知, 与 互为余角,求 的度数.
例1
因为 与 互为余角(已知),
所以(余角定义),
所以.
因为,
解:
所以.
应用新知
一个角比它的余角大 ,求这个角的度数.
例2
设这个角为 .
分析
根据余角的定义,它的余角表示为,
题目中的数量关系:这个角它的余角.
应用新知
设这个角为 ,依题意得:
答:这个角为 .
解:
一个角比它的余角大 ,求这个角的度数.
例2
如图,点 ,, 在同一直线上,射线 和射线 分别平分 和,
例3
求 的度数;
;
.
分析
因为点,, 在同一直线上,
所以.
又因为射线 和射线 分别平分 和,
所以
解:
.
如图,点 ,, 在同一直线上,射线 和射线 分别平分 和,
例3
求 的度数;
所以.
;
解:
如图,点 ,, 在同一直线上,射线 和射线 分别平分 和,
例3
图中哪些角互为余角?
.
;
;
课
堂
小
结
因为 与 互为余角,
所以.
因为,
所以 与 互为余角.
.余角的概念
和为 的两个角互为余角.
课
堂
小
结
因为,
所以.
因为,,且,
所以.
.余角的性质
同角(等角)的余角相等.
课后作业
如图,三角形 中,,, ,求 的度数.
再 见
