4.3.2.2 角的运算 课件(共30张PPT)
文档属性
| 名称 | 4.3.2.2 角的运算 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 20:00:22 | ||
图片预览


文档简介
(共30张PPT)
角
(第三课时)
复习回顾
角的大小比较
’
度量法
用量角器量出 与 的度数,就可以比较它们的大小了.
比如,,
所以 .
复习回顾
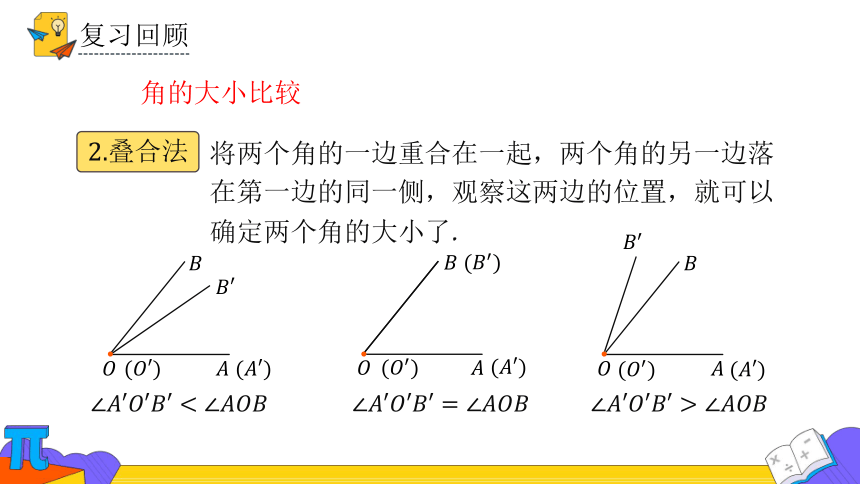
将两个角的一边重合在一起,两个角的另一边落在第一边的同一侧,观察这两边的位置,就可以确定两个角的大小了.
角的大小比较
叠合法
复习回顾
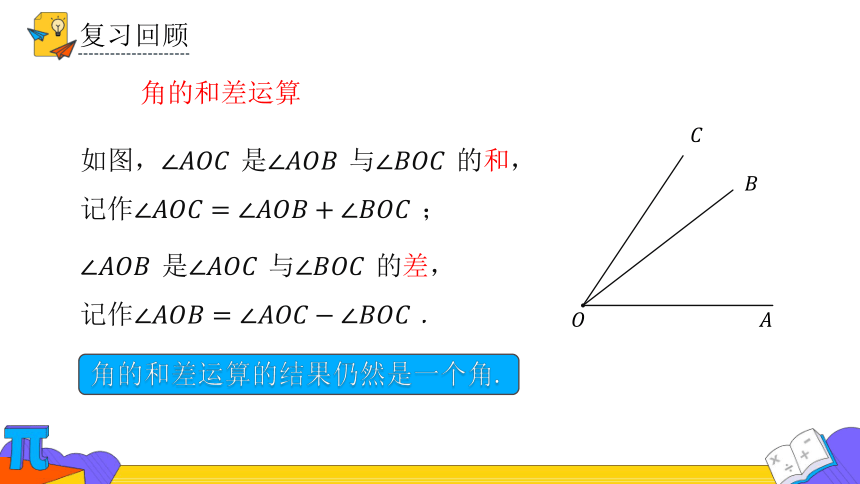
角的和差运算
如图, 是 与 的和,
记作 ;
是 与 的差,
记作 .
角的和差运算的结果仍然是一个角.
引入新知
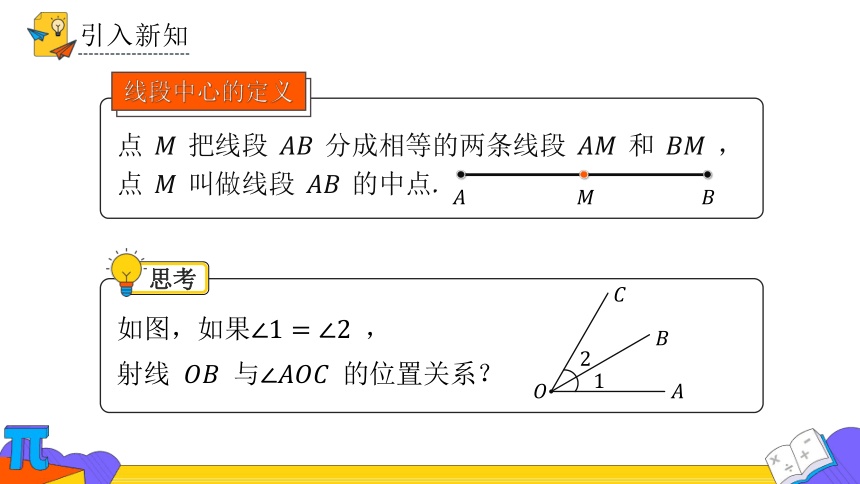
点 把线段 分成相等的两条线段 和 ,点 叫做线段 的中点.
如图,如果 ,
射线 与 的位置关系?
线段中心的定义
思考
学习新知
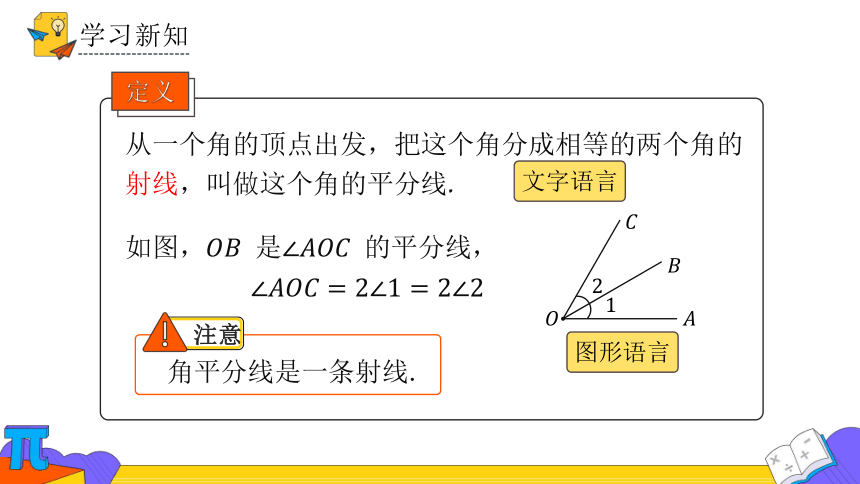
如图, 是 的平分线,
角平分线是一条射线.
注意
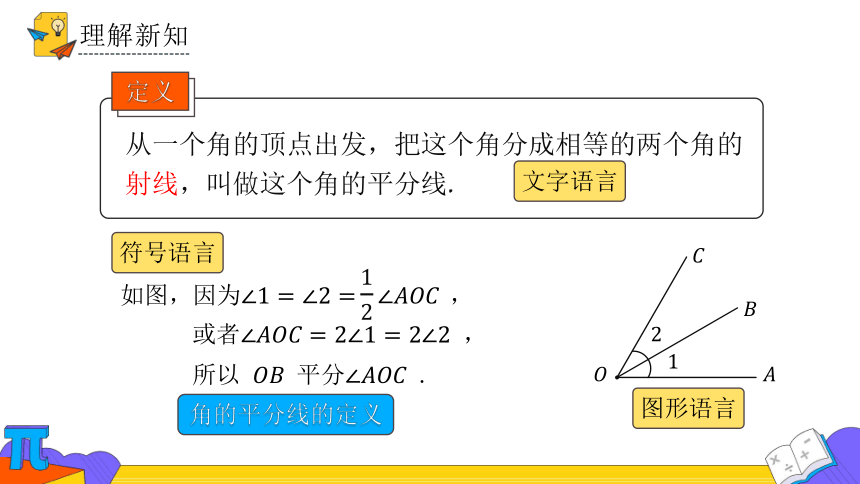
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.
定义
文字语言
图形语言
理解新知
或者 ,
所以 平分 .
角的平分线的定义
如图,因为 ,
图形语言
符号语言
文字语言
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.
定义
理解新知
图形语言
符号语言
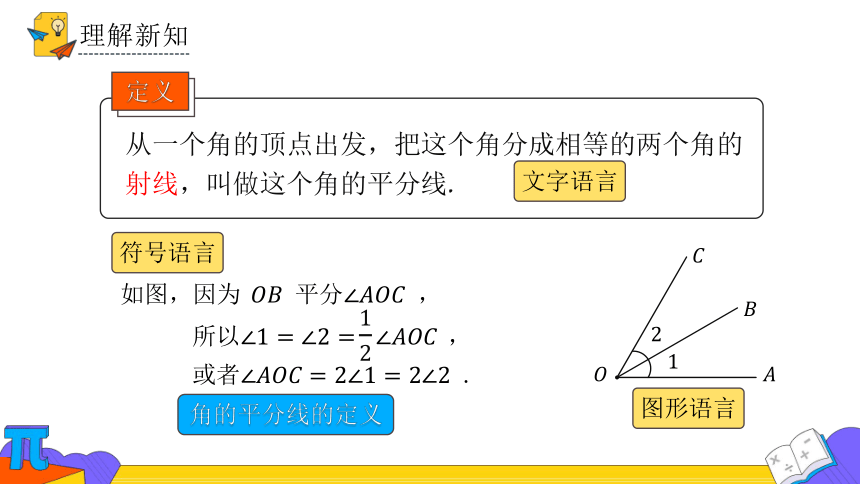
或者 .
如图,因为 平分 ,
角的平分线的定义
所以 ,
文字语言
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.
定义
理解新知
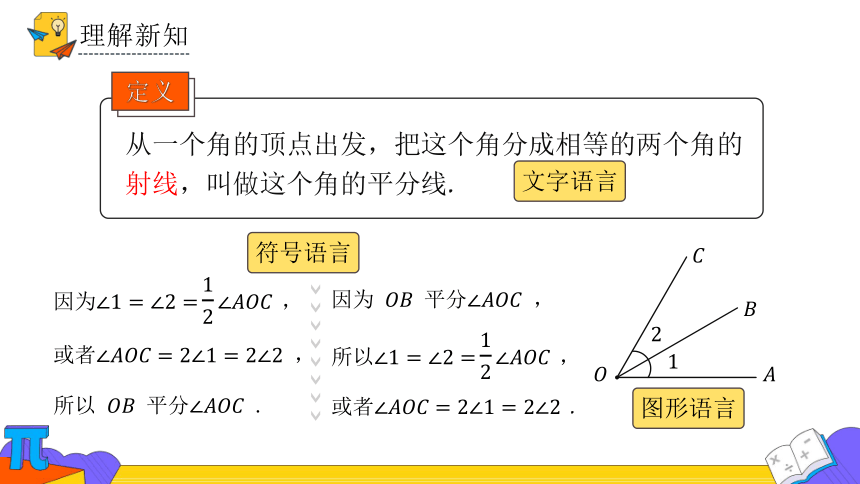
因为 ,
或者 ,
所以 平分 .
因为 平分 ,
所以 ,
或者 .
图形语言
符号语言
文字语言
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.
定义
学习新知
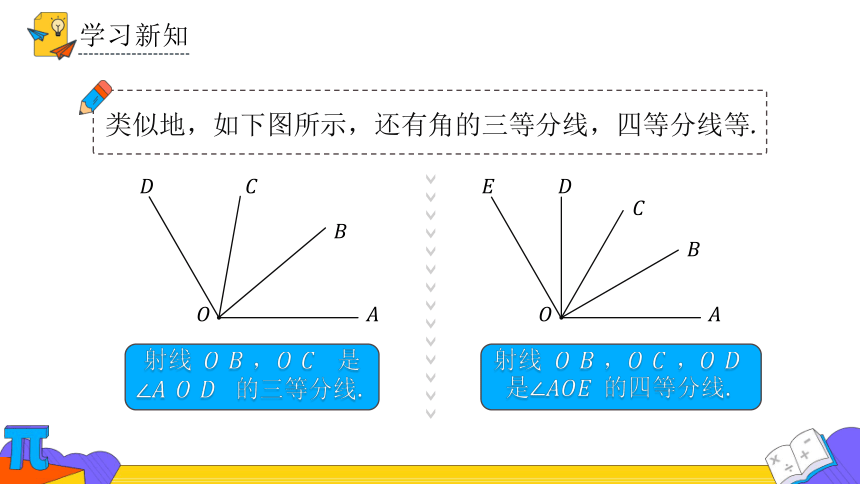
类似地,如下图所示,还有角的三等分线,四等分线等.
射线 , 是
的三等分线.
射线 , , 是 的四等分线.
学习新知
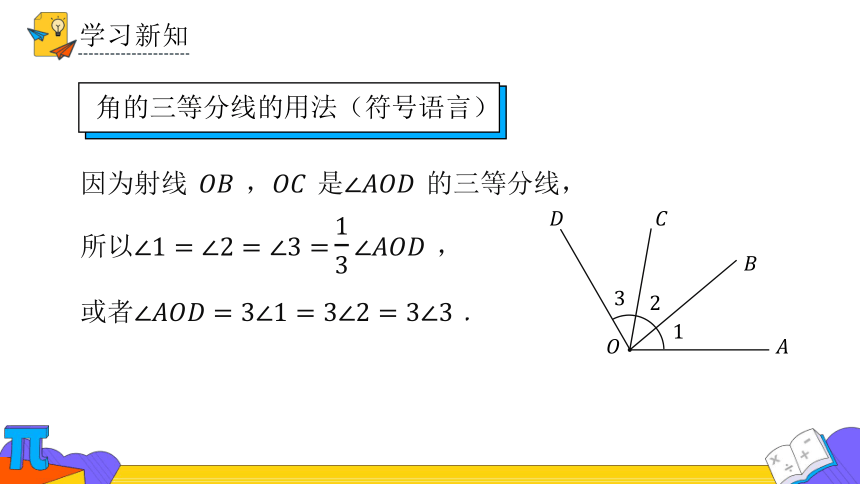
因为射线 , 是 的三等分线,
所以 ,
或者 .
角的三等分线的用法(符号语言)
学习新知
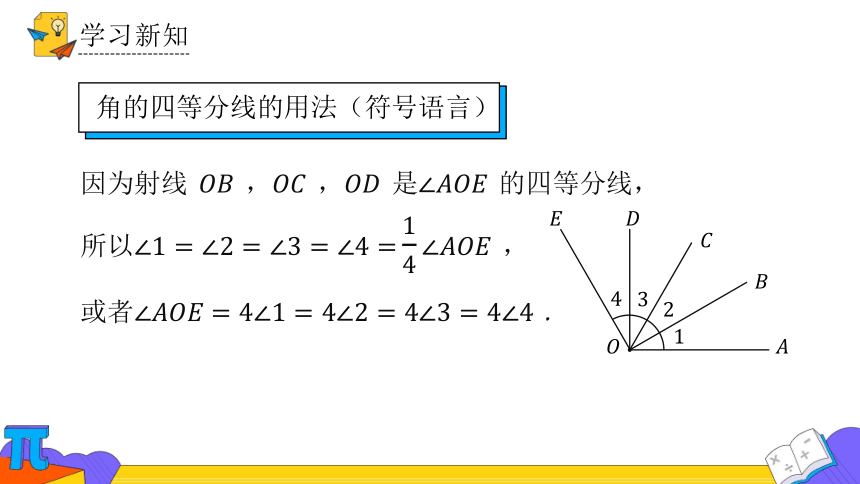
因为射线 , , 是 的四等分线,
所以 ,
或者 .
角的四等分线的用法(符号语言)
学习新知
方法
用量角器,可以作出一个角的平分线.
如何作出一个角的平分线?
探究
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.
定义
方法
学习新知
通过折纸作角平分线.
还有其他方法吗?
思考
例题讲解
如图,已知 是 的平分线, 是 的平
分线,若,求 的度数.
由角平分线的定义可以得
,
因为,
所以可以求 的度数.
例1
,
分析
例1
例题讲解
.
因为射线 分别是 的平分线,
所以 , ,
因为,
所以,
解:
如图,已知 是 的平分线, 是 的平
分线,若,求 的度数.
分析
如图,, 在 的内部, 平分 , 平分 ,求 的度数.
例2
例题讲解
例题讲解
因为 平分 , 平分 ,
所以 , ,
所以
因为,
所以 .
解:
如图, 是直角, ,平分 , 平分 ,求 的度数.
例3
例题讲解
,
,
分析
例题讲解
因为 平分 , 平分 ,
所以 , ,
所以
因为 是直角,即,
所以 .
解:
如图,直线 交于点 ,, 平分 , 为 的反向延长线.
例4
例题讲解
由平角可以得
;
由角平分线定义可得 ,
进而 .
求 , 的度数;
分析
例4
例题讲解
解:
.
因为直线 , 交于点 ,
所以,
因为,
进而
如图,直线 交于点 ,, 平分 , 为 的反向延长线.
求 , 的度数;
所以 ,
例4
因为 平分 ,
因为 为 的反向延长线,
.
所以,
所以
例题讲解
解:
如图,直线 交于点 ,, 平分 , 为 的反向延长线.
求 , 的度数;
例4
平分 吗?
例题讲解
,
通过计算得出,
所以 平分 .
°
分析
如图,直线 交于点 ,, 平分 , 为 的反向延长线.
例4
例题讲解
所以,
解:
因为 是直线,
所以
所以 平分 .
所以,
,
平分 吗?
如图,直线 交于点 ,, 平分 , 为 的反向延长线.
定义(文字语言)
角的平分线的定义及其三种语言表示:
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.
角平分线是一条射线.
注意
图形语言
课
堂
小
结
对折
角的平分线的定义及其三种语言表示:
符号语言
因为 ,
或者 ,
所以 平分 .
因为 平分 ,
所以 ,
或者 .
课
堂
小
结
课后拓展
如图,, 分别平分 和 ,已知任意三
角形的内角和为 ,若,求 的度数.
因为任意三角形的内角和为 ,
可求,
进而 ,
再利用三角形 求 的度数.
, ,
分析
课后拓展
因为 平分 , 平分 ,
所以 , .
因为任意三角形的内角和为 ,
所以.
所以 ,
解:
所以,
,
因为,
所以,
再 见
角
(第三课时)
复习回顾
角的大小比较
’
度量法
用量角器量出 与 的度数,就可以比较它们的大小了.
比如,,
所以 .
复习回顾
将两个角的一边重合在一起,两个角的另一边落在第一边的同一侧,观察这两边的位置,就可以确定两个角的大小了.
角的大小比较
叠合法
复习回顾
角的和差运算
如图, 是 与 的和,
记作 ;
是 与 的差,
记作 .
角的和差运算的结果仍然是一个角.
引入新知
点 把线段 分成相等的两条线段 和 ,点 叫做线段 的中点.
如图,如果 ,
射线 与 的位置关系?
线段中心的定义
思考
学习新知
如图, 是 的平分线,
角平分线是一条射线.
注意
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.
定义
文字语言
图形语言
理解新知
或者 ,
所以 平分 .
角的平分线的定义
如图,因为 ,
图形语言
符号语言
文字语言
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.
定义
理解新知
图形语言
符号语言
或者 .
如图,因为 平分 ,
角的平分线的定义
所以 ,
文字语言
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.
定义
理解新知
因为 ,
或者 ,
所以 平分 .
因为 平分 ,
所以 ,
或者 .
图形语言
符号语言
文字语言
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.
定义
学习新知
类似地,如下图所示,还有角的三等分线,四等分线等.
射线 , 是
的三等分线.
射线 , , 是 的四等分线.
学习新知
因为射线 , 是 的三等分线,
所以 ,
或者 .
角的三等分线的用法(符号语言)
学习新知
因为射线 , , 是 的四等分线,
所以 ,
或者 .
角的四等分线的用法(符号语言)
学习新知
方法
用量角器,可以作出一个角的平分线.
如何作出一个角的平分线?
探究
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.
定义
方法
学习新知
通过折纸作角平分线.
还有其他方法吗?
思考
例题讲解
如图,已知 是 的平分线, 是 的平
分线,若,求 的度数.
由角平分线的定义可以得
,
因为,
所以可以求 的度数.
例1
,
分析
例1
例题讲解
.
因为射线 分别是 的平分线,
所以 , ,
因为,
所以,
解:
如图,已知 是 的平分线, 是 的平
分线,若,求 的度数.
分析
如图,, 在 的内部, 平分 , 平分 ,求 的度数.
例2
例题讲解
例题讲解
因为 平分 , 平分 ,
所以 , ,
所以
因为,
所以 .
解:
如图, 是直角, ,平分 , 平分 ,求 的度数.
例3
例题讲解
,
,
分析
例题讲解
因为 平分 , 平分 ,
所以 , ,
所以
因为 是直角,即,
所以 .
解:
如图,直线 交于点 ,, 平分 , 为 的反向延长线.
例4
例题讲解
由平角可以得
;
由角平分线定义可得 ,
进而 .
求 , 的度数;
分析
例4
例题讲解
解:
.
因为直线 , 交于点 ,
所以,
因为,
进而
如图,直线 交于点 ,, 平分 , 为 的反向延长线.
求 , 的度数;
所以 ,
例4
因为 平分 ,
因为 为 的反向延长线,
.
所以,
所以
例题讲解
解:
如图,直线 交于点 ,, 平分 , 为 的反向延长线.
求 , 的度数;
例4
平分 吗?
例题讲解
,
通过计算得出,
所以 平分 .
°
分析
如图,直线 交于点 ,, 平分 , 为 的反向延长线.
例4
例题讲解
所以,
解:
因为 是直线,
所以
所以 平分 .
所以,
,
平分 吗?
如图,直线 交于点 ,, 平分 , 为 的反向延长线.
定义(文字语言)
角的平分线的定义及其三种语言表示:
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.
角平分线是一条射线.
注意
图形语言
课
堂
小
结
对折
角的平分线的定义及其三种语言表示:
符号语言
因为 ,
或者 ,
所以 平分 .
因为 平分 ,
所以 ,
或者 .
课
堂
小
结
课后拓展
如图,, 分别平分 和 ,已知任意三
角形的内角和为 ,若,求 的度数.
因为任意三角形的内角和为 ,
可求,
进而 ,
再利用三角形 求 的度数.
, ,
分析
课后拓展
因为 平分 , 平分 ,
所以 , .
因为任意三角形的内角和为 ,
所以.
所以 ,
解:
所以,
,
因为,
所以,
再 见
