反证法
图片预览





文档简介
课件15张PPT。14.1.3 反证法 学习目标
1、了解反证法的证明步骤,体会反证法证明问题的思
想,并能够运用反证法来证明一些问题;
2、理解并体会反证法的思想内涵;
3、通过反证法的学习,培养辩证唯物主义观念。
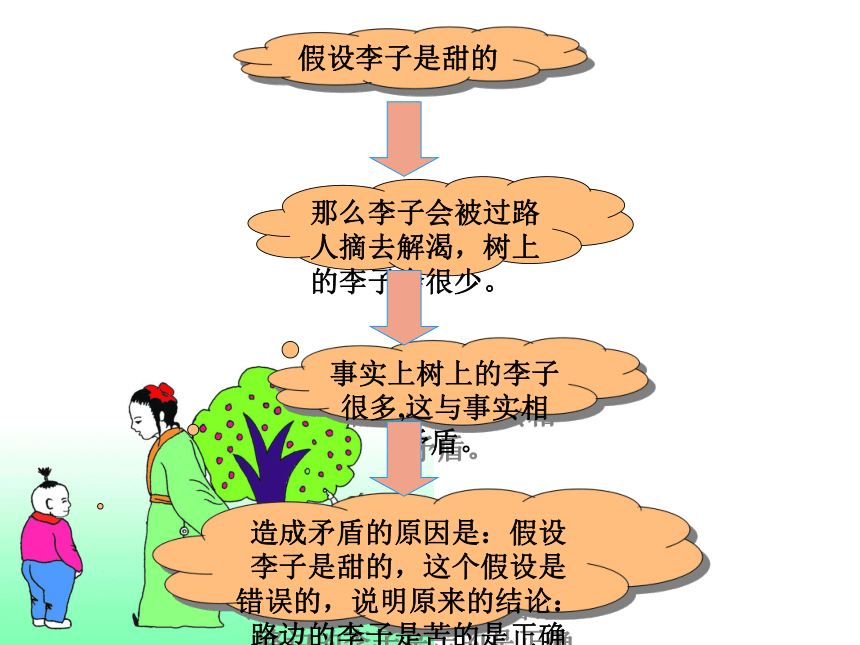
路边苦李 王戎7岁时,与小伙伴们外出游玩,看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动.有人问王戎为什么?王戎回答说:“树在道边而多子,此必苦李.”
小伙伴摘取一个尝了一下果然是苦李. 王戎是怎样知道李子是苦的呢?他运用了怎样的推理方法?假设李子是甜的那么李子会被过路人摘去解渴,树上的李子会很少。事实上树上的李子很多,这与事实相矛盾。造成矛盾的原因是:假设李子是甜的,这个假设是错误的,说明原来的结论:路边的李子是苦的是正确的。 在△ABC中,若AB≠AC,
则∠B≠∠C.如何说明呢?方 法 迁 移假设李子是甜的假设∠B=∠C那么AB=AC,
这与已知条件AB≠AC相矛盾假设不正确,则∠B≠∠C假设不正确,则李子是苦的。那么李子会被过路人摘去解渴,则李子会很少,这与事实相矛盾。
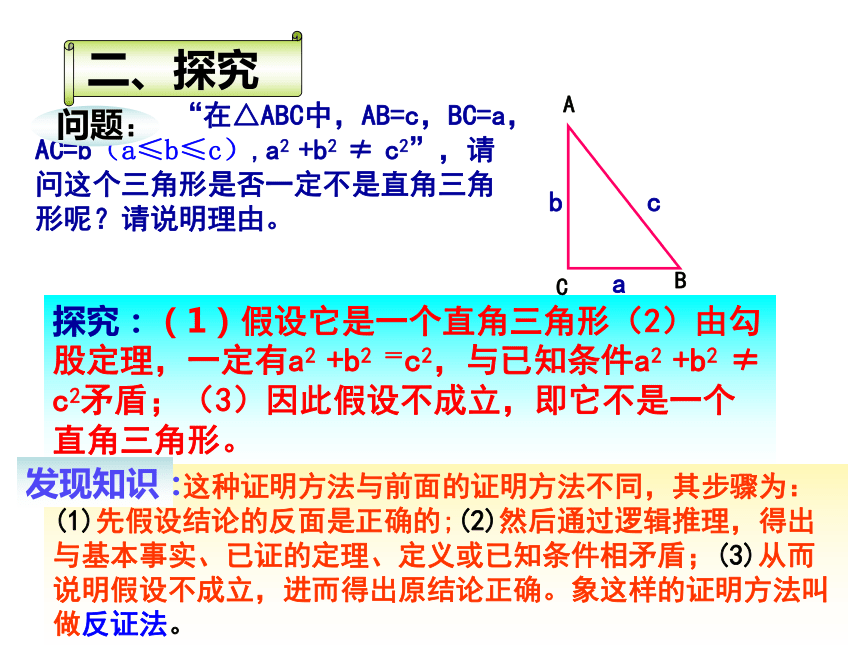
方法迁移探究:(1)假设它是一个直角三角形(2)由勾股定理,一定有a2 +b2 =c2,与已知条件a2 +b2 ≠ c2矛盾;(3)因此假设不成立,即它不是一个直角三角形。 这种证明方法与前面的证明方法不同,其步骤为:(1)先假设结论的反面是正确的;(2)然后通过逻辑推理,得出与基本事实、已证的定理、定义或已知条件相矛盾;(3)从而说明假设不成立,进而得出原结论正确。象这样的证明方法叫做反证法。发现知识:准确地作出反设(即否定结论)是非常重要的,下面是一些常见的关键词的否定形式. ?不是不都是不大于 不小于一个也没有至少有两个至多有(n-1)个至少有(n+1)个存在某个x不成立存在某个x,成立不等于某个证明:假设a与b不止一个交点,不妨假设有两个交点A和A’。
因为两点确定一条直线,即经过点A和A’的直线有且只有一条,这与已知两条直线矛盾,假设不成立。
所以两条直线相交只有一个交点。小结:根据假设推出结论除了可以与已知条件矛盾以外,还可以与我们学过的基本事实、定理矛盾求证:两条直线相交只有一个交点。已知:如图两条相交直线a、b。
求证:a与b只有一个交点。证明:假设a与b不平行,则可设它们相交于点A。
那么过点A 就有两条直线a、b与直线c平行,这与“过直线外一点有且只有一条直线与已知直线平行矛盾,假设不成立。
∴a//b.小结:根据假设推出结论除了可以与已知条件矛盾以外,还可以与我们学过的定理、公理矛盾 求证:在一个三角形中,至少有一个内角小于或等于60°。已知:△ABC
求证:△ABC中至少有一个内角小于或等于60°.证明:假设 ,
则 。
∴ ,
即 。
这与 矛盾.假设不成立.
∴ .△ABC中没有一个内角小于或等于60°∠A>60°,∠B>60°,∠C>60°∠A+∠B+∠C>180°三角形的内角和为180度△ABC中至少有一个内角小于或等于60°.点拨:至少的反面是没有!∠A+∠B+∠C>60°+60°+60°=180°假设结论的反面正确推理论证得出结论回顾与归纳反证法反设归谬结论证明真命题 的方法1、试说出下列命题的反面:
(1)a是实数。 (2)a大于2。
(3)a小于2。 (4)至少有2个
(5)最多有一个 (6)两条直线平行。
2、用反证法证明“若a2≠ b2,则a ≠ b”的第一步是 。
3、用反证法证明“如果一个三角形没有两个相等的角,那么这个三角形不是等腰三角形”的第一步
。 a不是实数 a小于或等于2 a大于或等于2没有两个一个也没有两直线相交假设a=b假设这个三角形是等腰三角形1、知识小结:
反证法证明的思路:假设命题不成立→正确的推理,得出矛盾→肯定待定命题的结论2、难点提示:
利用反证法证明命题时,一定要准确而全面的找出命题结论的反面。至少的反面是没有,最多的反面是不止。课时作业设计用反证法证明下列命题:
1.求证:三角形内角中至多有一个内角是钝角。
2.已知:如图,AB∥CD,AB ∥EF。
求证:CD ∥EF。
3.证明“在同一平面内,垂直于同一条直线的两条直线互相平行.”
1、了解反证法的证明步骤,体会反证法证明问题的思
想,并能够运用反证法来证明一些问题;
2、理解并体会反证法的思想内涵;
3、通过反证法的学习,培养辩证唯物主义观念。
路边苦李 王戎7岁时,与小伙伴们外出游玩,看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动.有人问王戎为什么?王戎回答说:“树在道边而多子,此必苦李.”
小伙伴摘取一个尝了一下果然是苦李. 王戎是怎样知道李子是苦的呢?他运用了怎样的推理方法?假设李子是甜的那么李子会被过路人摘去解渴,树上的李子会很少。事实上树上的李子很多,这与事实相矛盾。造成矛盾的原因是:假设李子是甜的,这个假设是错误的,说明原来的结论:路边的李子是苦的是正确的。 在△ABC中,若AB≠AC,
则∠B≠∠C.如何说明呢?方 法 迁 移假设李子是甜的假设∠B=∠C那么AB=AC,
这与已知条件AB≠AC相矛盾假设不正确,则∠B≠∠C假设不正确,则李子是苦的。那么李子会被过路人摘去解渴,则李子会很少,这与事实相矛盾。
方法迁移探究:(1)假设它是一个直角三角形(2)由勾股定理,一定有a2 +b2 =c2,与已知条件a2 +b2 ≠ c2矛盾;(3)因此假设不成立,即它不是一个直角三角形。 这种证明方法与前面的证明方法不同,其步骤为:(1)先假设结论的反面是正确的;(2)然后通过逻辑推理,得出与基本事实、已证的定理、定义或已知条件相矛盾;(3)从而说明假设不成立,进而得出原结论正确。象这样的证明方法叫做反证法。发现知识:准确地作出反设(即否定结论)是非常重要的,下面是一些常见的关键词的否定形式. ?不是不都是不大于 不小于一个也没有至少有两个至多有(n-1)个至少有(n+1)个存在某个x不成立存在某个x,成立不等于某个证明:假设a与b不止一个交点,不妨假设有两个交点A和A’。
因为两点确定一条直线,即经过点A和A’的直线有且只有一条,这与已知两条直线矛盾,假设不成立。
所以两条直线相交只有一个交点。小结:根据假设推出结论除了可以与已知条件矛盾以外,还可以与我们学过的基本事实、定理矛盾求证:两条直线相交只有一个交点。已知:如图两条相交直线a、b。
求证:a与b只有一个交点。证明:假设a与b不平行,则可设它们相交于点A。
那么过点A 就有两条直线a、b与直线c平行,这与“过直线外一点有且只有一条直线与已知直线平行矛盾,假设不成立。
∴a//b.小结:根据假设推出结论除了可以与已知条件矛盾以外,还可以与我们学过的定理、公理矛盾 求证:在一个三角形中,至少有一个内角小于或等于60°。已知:△ABC
求证:△ABC中至少有一个内角小于或等于60°.证明:假设 ,
则 。
∴ ,
即 。
这与 矛盾.假设不成立.
∴ .△ABC中没有一个内角小于或等于60°∠A>60°,∠B>60°,∠C>60°∠A+∠B+∠C>180°三角形的内角和为180度△ABC中至少有一个内角小于或等于60°.点拨:至少的反面是没有!∠A+∠B+∠C>60°+60°+60°=180°假设结论的反面正确推理论证得出结论回顾与归纳反证法反设归谬结论证明真命题 的方法1、试说出下列命题的反面:
(1)a是实数。 (2)a大于2。
(3)a小于2。 (4)至少有2个
(5)最多有一个 (6)两条直线平行。
2、用反证法证明“若a2≠ b2,则a ≠ b”的第一步是 。
3、用反证法证明“如果一个三角形没有两个相等的角,那么这个三角形不是等腰三角形”的第一步
。 a不是实数 a小于或等于2 a大于或等于2没有两个一个也没有两直线相交假设a=b假设这个三角形是等腰三角形1、知识小结:
反证法证明的思路:假设命题不成立→正确的推理,得出矛盾→肯定待定命题的结论2、难点提示:
利用反证法证明命题时,一定要准确而全面的找出命题结论的反面。至少的反面是没有,最多的反面是不止。课时作业设计用反证法证明下列命题:
1.求证:三角形内角中至多有一个内角是钝角。
2.已知:如图,AB∥CD,AB ∥EF。
求证:CD ∥EF。
3.证明“在同一平面内,垂直于同一条直线的两条直线互相平行.”
