3.1.1.2 一元一次方程 课件(共32张PPT)
文档属性
| 名称 | 3.1.1.2 一元一次方程 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 20:18:22 | ||
图片预览











文档简介
(共32张PPT)
一元一次方程
(第二课时)
复习回顾
分析题意,圈画关键词、列表或画图
1
设未知数,列方程.
2
列方程解实际问题初始的两步:
找出相等关系;
1
用一根长 的铁丝围成一个正方形,正方形的边长是多少
复习回顾
根据下列问题,设未知数并列出方程:
列方程
解:设正方形的边长为
分析
周长
一台计算机已使用,预计每月再使用,经过多少个月这台计算机的使用时间达到规定的检修时间?
2
分析
解:设经过 个月可达到规定的检修时间,则再使用时间为
列方程
根据下列问题,设未知数并列出方程:
某校女生占全体学生的,比男生多人,这个学校有多少学生?
3
根据下列问题,设未知数并列出方程:
分析
解:设这个学校有名学生,则女生人数为
列方程
人数为
某校女生占全体学生的,比男生多人,这个学校有多少学生?
3
根据下列问题,设未知数并列出方程:
分析
解:设这个学校有名男生,则女生人数为
列方程
全体学生人 数为
学习新知
;
;
只含有一个未知数
1
未知数的次数都是
2
观察这三个方程有什么共同特点?
学习新知
;
;
只含有一个未知数
1
未知数的次数都是
2
学习新知
;
;
只含有一个未知数
1
未知数的次数都是
2
学习新知
;
;
只含有一个未知数
1
未知数的次数都是
2
学习新知
;
;
只含有一个未知数
1
未知数的次数都是
2
等号两边都是整式
3
一元一次方程的定义:
只含有一个未知数,未知数的次数都是,等号两边都是整式,这样的方程叫做一元一次方程.
课堂练习
1
3
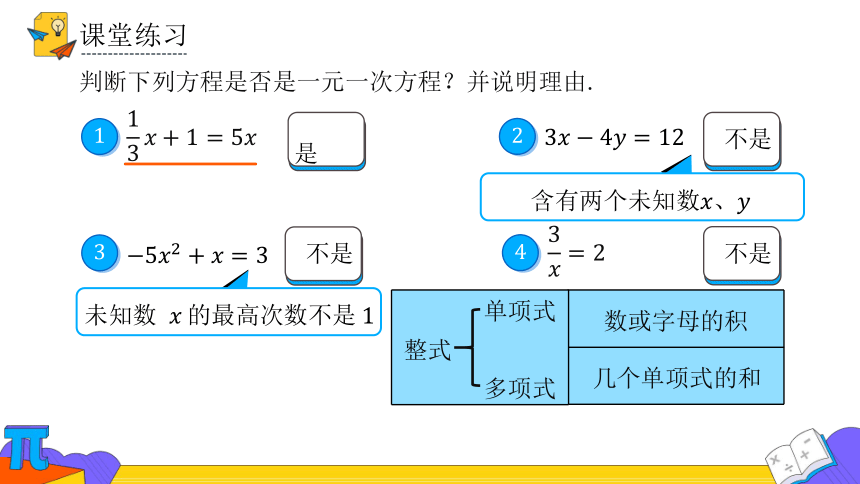
判断下列方程是否是一元一次方程?并说明理由.
2
4
是
不是
不是
两个未知数
未知数 最高次数不是
整式
单项式
多项式
数或字母的积
几个单项式的和
不是
提出问题
方程 中未知数的值是多少?
问题1
因为,
分析
叫做方程的解.
所以当 时,方程 左右两边的值相等.
方程 中未知数 的值是多少?
问题2
分析
根据下列问题,设未知数并列出方程:
一台计算机已使用,预计每月再使用,经过多少个月这台计算机的使用时间达到规定的检修时间?
2
解:设经过 个月可达到规定的检修时间,则再使用时间为
.
列方程
方程 中未知数 的值是多少?
问题2
分析
…
…
方程 中未知数 的值是多少?
问题2
分析
叫做方程 的解.
…
…
时方程
方程 中未知数 的值是多少?
问题2
任取未知数的值
等式成立
左右两边等式成立
得方程的解
代入
等式不成立
学习新知
解方程就是求出使方程中等号左
右两边相等的未知数的值,这个值就
是方程的解.
例题讲解
分析
的解
代入
等式成立
的解
等式不成立
,
,
所以
所以
,
,
所以
所以
课堂练习
各是下列哪个方程的解?
1
,
,
所以
所以
各是下列哪个方程的解?
1
,
,
所以
所以
各是下列哪个方程的解?
1
各是下列哪个方程的解?
1
,
,
所以
所以
各是下列哪个方程的解?
1
,
,
所以
所以
是否是方程
2
是否是方程解?
是否是方程
2
所以
所以
,
,
是否是方程解?
2
所以
所以
,
,
1. 一元一次方程的三个特征是什么?
只含有一个未知数
1
2
未知数的次数都是
3
等号两边都是整式
课
堂
小
结
课
堂
小
结
如:
的解
代入
等式成立
的解
等式不成立
2. 如何检验某个值是不是方程的解?
再 见
一元一次方程
(第二课时)
复习回顾
分析题意,圈画关键词、列表或画图
1
设未知数,列方程.
2
列方程解实际问题初始的两步:
找出相等关系;
1
用一根长 的铁丝围成一个正方形,正方形的边长是多少
复习回顾
根据下列问题,设未知数并列出方程:
列方程
解:设正方形的边长为
分析
周长
一台计算机已使用,预计每月再使用,经过多少个月这台计算机的使用时间达到规定的检修时间?
2
分析
解:设经过 个月可达到规定的检修时间,则再使用时间为
列方程
根据下列问题,设未知数并列出方程:
某校女生占全体学生的,比男生多人,这个学校有多少学生?
3
根据下列问题,设未知数并列出方程:
分析
解:设这个学校有名学生,则女生人数为
列方程
人数为
某校女生占全体学生的,比男生多人,这个学校有多少学生?
3
根据下列问题,设未知数并列出方程:
分析
解:设这个学校有名男生,则女生人数为
列方程
全体学生人 数为
学习新知
;
;
只含有一个未知数
1
未知数的次数都是
2
观察这三个方程有什么共同特点?
学习新知
;
;
只含有一个未知数
1
未知数的次数都是
2
学习新知
;
;
只含有一个未知数
1
未知数的次数都是
2
学习新知
;
;
只含有一个未知数
1
未知数的次数都是
2
学习新知
;
;
只含有一个未知数
1
未知数的次数都是
2
等号两边都是整式
3
一元一次方程的定义:
只含有一个未知数,未知数的次数都是,等号两边都是整式,这样的方程叫做一元一次方程.
课堂练习
1
3
判断下列方程是否是一元一次方程?并说明理由.
2
4
是
不是
不是
两个未知数
未知数 最高次数不是
整式
单项式
多项式
数或字母的积
几个单项式的和
不是
提出问题
方程 中未知数的值是多少?
问题1
因为,
分析
叫做方程的解.
所以当 时,方程 左右两边的值相等.
方程 中未知数 的值是多少?
问题2
分析
根据下列问题,设未知数并列出方程:
一台计算机已使用,预计每月再使用,经过多少个月这台计算机的使用时间达到规定的检修时间?
2
解:设经过 个月可达到规定的检修时间,则再使用时间为
.
列方程
方程 中未知数 的值是多少?
问题2
分析
…
…
方程 中未知数 的值是多少?
问题2
分析
叫做方程 的解.
…
…
时方程
方程 中未知数 的值是多少?
问题2
任取未知数的值
等式成立
左右两边等式成立
得方程的解
代入
等式不成立
学习新知
解方程就是求出使方程中等号左
右两边相等的未知数的值,这个值就
是方程的解.
例题讲解
分析
的解
代入
等式成立
的解
等式不成立
,
,
所以
所以
,
,
所以
所以
课堂练习
各是下列哪个方程的解?
1
,
,
所以
所以
各是下列哪个方程的解?
1
,
,
所以
所以
各是下列哪个方程的解?
1
各是下列哪个方程的解?
1
,
,
所以
所以
各是下列哪个方程的解?
1
,
,
所以
所以
是否是方程
2
是否是方程解?
是否是方程
2
所以
所以
,
,
是否是方程解?
2
所以
所以
,
,
1. 一元一次方程的三个特征是什么?
只含有一个未知数
1
2
未知数的次数都是
3
等号两边都是整式
课
堂
小
结
课
堂
小
结
如:
的解
代入
等式成立
的解
等式不成立
2. 如何检验某个值是不是方程的解?
再 见
