3.2.3 解一元一次方程(一)——合并同类项与移项 课件(共35张PPT)
文档属性
| 名称 | 3.2.3 解一元一次方程(一)——合并同类项与移项 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 20:16:12 | ||
图片预览











文档简介
(共35张PPT)
(第三课时)
解一元一次方程(一)
复习回顾
通过移项这个变形过程,将所给方程中含有未知数的项和常数项分别移到方程的两侧. 然后,通过合并同类项和系数化为等步骤,将方程变形为的形式,得到方程的解.
复习回顾
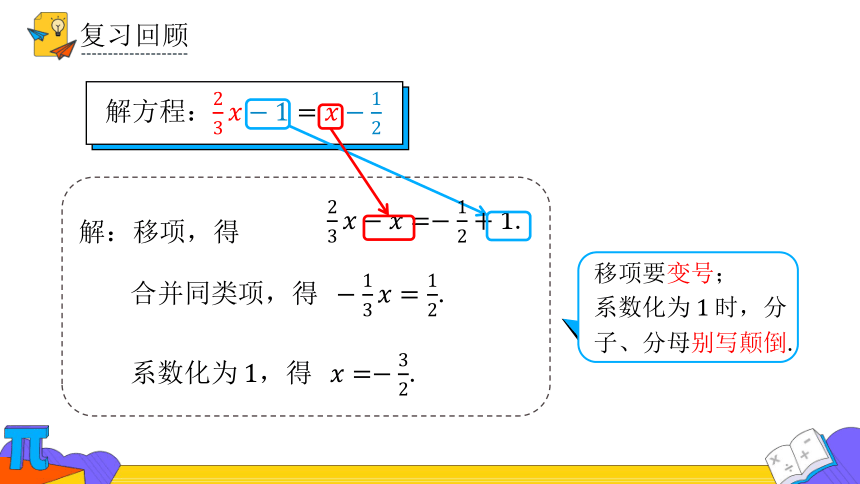
解方程:
.
复习回顾
解方程:
:移项,得
同类项,得.
系数化为,得.
移项要变号;
系数化为时,分子、分母别写颠倒.
学习新知
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多;如用新工艺,则废水排量要比环保限制的最大量少. 新、旧工艺的废水排量之比为:,两种工艺的废水排量各是多少?
例1
学习新知
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多;如用新工艺,则废水排量要比环保限制的最大量少. 新、旧工艺的废水排量之比为:,两种工艺的废水排量各是多少?
例1
旧工艺废水排量环保限制的最大量,
分析
学习新知
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多;如用新工艺,则废水排量要比环保限制的最大量少. 新、旧工艺的废水排量之比为:,两种工艺的废水排量各是多少?
例1
旧工艺废水排量环保限制的最大量,
新工艺废水排量环保限制的最大量,
分析
②
学习新知
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多;如用新工艺,则废水排量要比环保限制的最大量少. 新、旧工艺的废水排量之比为:,两种工艺的废水排量各是多少?
例1
旧工艺废水排量环保限制的最大量,
新工艺废水排量环保限制的最大量,
新工艺废水排量 : 旧工艺废水排量:.
③
分析
②
旧工艺废水排量环保限制的最大量,
分析
新工艺废水排量环保限制的最大量,
新工艺废水排量 : 旧工艺废水排量:.
怎样设未知数,并表示相关的未知量更好?
设新工艺废水排量为,根据条件 ,旧工艺废水排量 .
根据条件 ,可设新、旧工艺的废水排量分别为和 .
学习新知
③
②
学习新知
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多;如用新工艺,则废水排量要比环保限制的最大量少. 新、旧工艺的废水排量之比为:,两种工艺的废水排量各是多少?
例1
设新、旧工艺的废水排量分别为和 .
环保限制的最大量. ①
环保限制的最大量. ②
环保限制的最大量.
环保限制的最大量.
分析
学习新知
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多;如用新工艺,则废水排量要比环保限制的最大量少. 新、旧工艺的废水排量之比为:,两种工艺的废水排量各是多少?
例1
如何求解这个方程呢?
解:
设新、旧工艺的废水排量分别为和.
根据废水排量与环保限制最大量之间的关系,
得.
学习新知
如何求解呢?
移项,得.
合并同类项,得.
系数化为,得.
想一想,这个问题解决了吗?
解:设新、旧工艺的废水排量分别为和 .
根据废水排量与环保限制最大量之间的关系,得
移项,得.
合并同类项,得.
系数化为,得.
所以, .
答:新、旧工艺产生的废水排量分别为和.
还可以怎样列方程?
学习新知
.
根据条件 ,可设新、旧工艺的废水排量分别为和 .
根据条件 ,可得环保限制的最大量为,
代入条件 ,可得新工艺废水排量为,
于是可列方程.
学习新知
环保限制的最大量. ①
环保限制的最大量. ②
分析
根据条件 ,可设新、旧工艺的废水排量分别为和 .
根据条件 ,可得环保限制的最大量为,
代入条件 ,可得旧工艺废水排量为,
于是可列方程.
还有不同的设法吗?
学习新知
环保限制的最大量. ①
环保限制的最大量. ②
分析
旧工艺废水排量环保限制的最大量,
新工艺废水排量环保限制的最大量,
新工艺废水排量 : 旧工艺废水排量:.
③
设环保限制的最大量为,
根据条件 ,得旧工艺的废水排量为,
学习新知
根据条件 ,得新工艺的废水排量为 ,
根据条件 ,可列方程 .
分析
设新工艺废水排量为,
学习新知
根据条件 ,得环保限制的最大量为,
根据条件 ,得旧工艺废水排量为 ,
根据条件 ,可列方程 .
旧工艺废水排量环保限制的最大量,
新工艺废水排量环保限制的最大量,
新工艺废水排量 : 旧工艺废水排量:.
③
分析
学习新知
.
.
.
学习新知
1
3
2
4
审题——勾画关键词,找出相等关系;
表示相等关系;
设未知数,列方程;
解方程、检验,并答题.
.列方程解应用题的步骤:
小结
学习新知
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多;如用新工艺,则废水排量要比环保限制的最大量少. 新、旧工艺的废水排量之比为:,两种工艺的废水排量各是多少?
例1
旧工艺废水排量环保限制的最大量,
新工艺废水排量环保限制的最大量,
新工艺废水排量 : 旧工艺废水排量:.
②
.观察未知量的特点,选择合适的方式设未知数.
③
①
学以致用
洗衣机厂今年计划生产洗衣机台,其中型、型、型三种洗衣机的数量比为::,计划生产这三种洗衣机各多少台?
练习1
学以致用
洗衣机厂今年计划生产洗衣机台,其中型、型、型三种洗衣机的数量比为::,计划生产这三种洗衣机各多少台?
练习1
因为、、型三种洗衣机的数量之比为::,所以可设这三种型号洗衣机的数量分别为台、台、台,再根据这三种洗衣机数量之和为台,列方程.
分析
学以致用
解:设计划生产三种洗衣机各台、台、台.
根据三种洗衣机数量之和为,得
.
合并同类项,得
系数化为,得.
所以, .
答:这三种洗衣机各、和台.
.
学以致用
把一根长的木棍锯成两段,要使其中一段长比另一段长的倍少,应该在木棍的哪个位置锯开?
练习2
一段长另一段长,
一段长另一段长.
分析
①
②
学以致用
把一根长的木棍锯成两段,要使其中一段长比另一段长的倍少,应该在木棍的哪个位置锯开?
练习2
一段长另一段长,
一段长另一段长.
分析
①
②
学以致用
把一根长的木棍锯成两段,要使其中一段长比另一段长的倍少,应该在木棍的哪个位置锯开?
练习2
一段长另一段长,
一段长另一段长.
分析
①
②
学以致用
把一根长的木棍锯成两段,要使其中一段长比另一段长的倍少,应该在木棍的哪个位置锯开?
练习2
一段长另一段长,
一段长另一段长.
分析
①
②
一段长另一段长,
一段长另一段长.
学以致用
把一根长的木棍锯成两段,要使其中一段长比另一段长的倍少,应该在木棍的哪个位置锯开?
练习2
怎样设未知数,并表示相关的未知量更好?
分析
①
②
学以致用
把一根长的木棍锯成两段,要使其中一段长比另一段长的倍少,应该在木棍的哪个位置锯开?
练习2
设在距木棍一端处锯开.
根据另一段木棍长度,列出方程
.
解:
解:设在距木棍一端处锯开.
根据另一段木棍长度,列出方程
合并同类项,得
系数化为,得
答:距一端处锯开.
学以致用
移项,得
.
.
.
.
1
审题;表示相等关系;
设未知数列方程;求解检验并答题;
列方程解应用题的步骤:
2
如 解方程:
解:移项,得
解方程移项要变号;
合并同类项,得
系数化为,得
课
堂
小
结
.
.
.
.
课后思考
在一张普通的月历中,相邻三行里同一列的三个日期数之和能否为?如果能,这三个数分别是多少?
课后思考
在一张普通的月历中,相邻三行里同一列的三个日期数之和能否为?如果能,这三个数分别是多少?
相邻三行里同一列的上、中、下三个日期数字中,后一个比前一个大;
分析
1
课后思考
相邻三行里同一列的上、中、下三个日期数字中,后一个比前一个大;
分析
1
2
上中下.
在一张普通的月历中,相邻三行里同一列的三个日期数之和能否为?如果能,这三个数分别是多少?
再 见
(第三课时)
解一元一次方程(一)
复习回顾
通过移项这个变形过程,将所给方程中含有未知数的项和常数项分别移到方程的两侧. 然后,通过合并同类项和系数化为等步骤,将方程变形为的形式,得到方程的解.
复习回顾
解方程:
.
复习回顾
解方程:
:移项,得
同类项,得.
系数化为,得.
移项要变号;
系数化为时,分子、分母别写颠倒.
学习新知
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多;如用新工艺,则废水排量要比环保限制的最大量少. 新、旧工艺的废水排量之比为:,两种工艺的废水排量各是多少?
例1
学习新知
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多;如用新工艺,则废水排量要比环保限制的最大量少. 新、旧工艺的废水排量之比为:,两种工艺的废水排量各是多少?
例1
旧工艺废水排量环保限制的最大量,
分析
学习新知
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多;如用新工艺,则废水排量要比环保限制的最大量少. 新、旧工艺的废水排量之比为:,两种工艺的废水排量各是多少?
例1
旧工艺废水排量环保限制的最大量,
新工艺废水排量环保限制的最大量,
分析
②
学习新知
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多;如用新工艺,则废水排量要比环保限制的最大量少. 新、旧工艺的废水排量之比为:,两种工艺的废水排量各是多少?
例1
旧工艺废水排量环保限制的最大量,
新工艺废水排量环保限制的最大量,
新工艺废水排量 : 旧工艺废水排量:.
③
分析
②
旧工艺废水排量环保限制的最大量,
分析
新工艺废水排量环保限制的最大量,
新工艺废水排量 : 旧工艺废水排量:.
怎样设未知数,并表示相关的未知量更好?
设新工艺废水排量为,根据条件 ,旧工艺废水排量 .
根据条件 ,可设新、旧工艺的废水排量分别为和 .
学习新知
③
②
学习新知
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多;如用新工艺,则废水排量要比环保限制的最大量少. 新、旧工艺的废水排量之比为:,两种工艺的废水排量各是多少?
例1
设新、旧工艺的废水排量分别为和 .
环保限制的最大量. ①
环保限制的最大量. ②
环保限制的最大量.
环保限制的最大量.
分析
学习新知
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多;如用新工艺,则废水排量要比环保限制的最大量少. 新、旧工艺的废水排量之比为:,两种工艺的废水排量各是多少?
例1
如何求解这个方程呢?
解:
设新、旧工艺的废水排量分别为和.
根据废水排量与环保限制最大量之间的关系,
得.
学习新知
如何求解呢?
移项,得.
合并同类项,得.
系数化为,得.
想一想,这个问题解决了吗?
解:设新、旧工艺的废水排量分别为和 .
根据废水排量与环保限制最大量之间的关系,得
移项,得.
合并同类项,得.
系数化为,得.
所以, .
答:新、旧工艺产生的废水排量分别为和.
还可以怎样列方程?
学习新知
.
根据条件 ,可设新、旧工艺的废水排量分别为和 .
根据条件 ,可得环保限制的最大量为,
代入条件 ,可得新工艺废水排量为,
于是可列方程.
学习新知
环保限制的最大量. ①
环保限制的最大量. ②
分析
根据条件 ,可设新、旧工艺的废水排量分别为和 .
根据条件 ,可得环保限制的最大量为,
代入条件 ,可得旧工艺废水排量为,
于是可列方程.
还有不同的设法吗?
学习新知
环保限制的最大量. ①
环保限制的最大量. ②
分析
旧工艺废水排量环保限制的最大量,
新工艺废水排量环保限制的最大量,
新工艺废水排量 : 旧工艺废水排量:.
③
设环保限制的最大量为,
根据条件 ,得旧工艺的废水排量为,
学习新知
根据条件 ,得新工艺的废水排量为 ,
根据条件 ,可列方程 .
分析
设新工艺废水排量为,
学习新知
根据条件 ,得环保限制的最大量为,
根据条件 ,得旧工艺废水排量为 ,
根据条件 ,可列方程 .
旧工艺废水排量环保限制的最大量,
新工艺废水排量环保限制的最大量,
新工艺废水排量 : 旧工艺废水排量:.
③
分析
学习新知
.
.
.
学习新知
1
3
2
4
审题——勾画关键词,找出相等关系;
表示相等关系;
设未知数,列方程;
解方程、检验,并答题.
.列方程解应用题的步骤:
小结
学习新知
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多;如用新工艺,则废水排量要比环保限制的最大量少. 新、旧工艺的废水排量之比为:,两种工艺的废水排量各是多少?
例1
旧工艺废水排量环保限制的最大量,
新工艺废水排量环保限制的最大量,
新工艺废水排量 : 旧工艺废水排量:.
②
.观察未知量的特点,选择合适的方式设未知数.
③
①
学以致用
洗衣机厂今年计划生产洗衣机台,其中型、型、型三种洗衣机的数量比为::,计划生产这三种洗衣机各多少台?
练习1
学以致用
洗衣机厂今年计划生产洗衣机台,其中型、型、型三种洗衣机的数量比为::,计划生产这三种洗衣机各多少台?
练习1
因为、、型三种洗衣机的数量之比为::,所以可设这三种型号洗衣机的数量分别为台、台、台,再根据这三种洗衣机数量之和为台,列方程.
分析
学以致用
解:设计划生产三种洗衣机各台、台、台.
根据三种洗衣机数量之和为,得
.
合并同类项,得
系数化为,得.
所以, .
答:这三种洗衣机各、和台.
.
学以致用
把一根长的木棍锯成两段,要使其中一段长比另一段长的倍少,应该在木棍的哪个位置锯开?
练习2
一段长另一段长,
一段长另一段长.
分析
①
②
学以致用
把一根长的木棍锯成两段,要使其中一段长比另一段长的倍少,应该在木棍的哪个位置锯开?
练习2
一段长另一段长,
一段长另一段长.
分析
①
②
学以致用
把一根长的木棍锯成两段,要使其中一段长比另一段长的倍少,应该在木棍的哪个位置锯开?
练习2
一段长另一段长,
一段长另一段长.
分析
①
②
学以致用
把一根长的木棍锯成两段,要使其中一段长比另一段长的倍少,应该在木棍的哪个位置锯开?
练习2
一段长另一段长,
一段长另一段长.
分析
①
②
一段长另一段长,
一段长另一段长.
学以致用
把一根长的木棍锯成两段,要使其中一段长比另一段长的倍少,应该在木棍的哪个位置锯开?
练习2
怎样设未知数,并表示相关的未知量更好?
分析
①
②
学以致用
把一根长的木棍锯成两段,要使其中一段长比另一段长的倍少,应该在木棍的哪个位置锯开?
练习2
设在距木棍一端处锯开.
根据另一段木棍长度,列出方程
.
解:
解:设在距木棍一端处锯开.
根据另一段木棍长度,列出方程
合并同类项,得
系数化为,得
答:距一端处锯开.
学以致用
移项,得
.
.
.
.
1
审题;表示相等关系;
设未知数列方程;求解检验并答题;
列方程解应用题的步骤:
2
如 解方程:
解:移项,得
解方程移项要变号;
合并同类项,得
系数化为,得
课
堂
小
结
.
.
.
.
课后思考
在一张普通的月历中,相邻三行里同一列的三个日期数之和能否为?如果能,这三个数分别是多少?
课后思考
在一张普通的月历中,相邻三行里同一列的三个日期数之和能否为?如果能,这三个数分别是多少?
相邻三行里同一列的上、中、下三个日期数字中,后一个比前一个大;
分析
1
课后思考
相邻三行里同一列的上、中、下三个日期数字中,后一个比前一个大;
分析
1
2
上中下.
在一张普通的月历中,相邻三行里同一列的三个日期数之和能否为?如果能,这三个数分别是多少?
再 见
