3.3.4 解一元一次方程(二)——去括号与去分母 课件(共14张PPT)
文档属性
| 名称 | 3.3.4 解一元一次方程(二)——去括号与去分母 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 20:12:26 | ||
图片预览




文档简介
(共14张PPT)
(第四课时)
解一元一次方程(二)
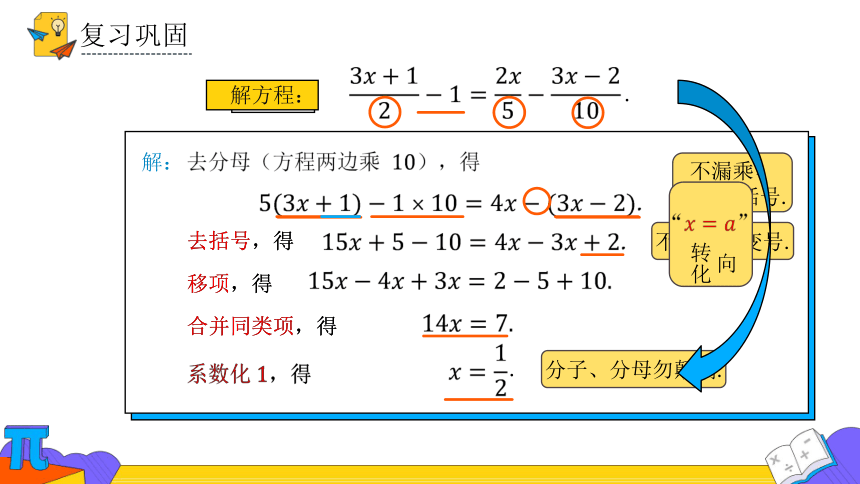
复习巩固
解方程:
解:
去分母(方程两边乘 ),得
.
去括号,得
.
移项,得
系数化,得
.
合并同类项,得
.
去括号,得
移项,得
系数化,得
合并同类项,得
不漏乘、
分子加括号.
不漏乘、变号.
分子、分母勿颠倒.
向 转化
“”
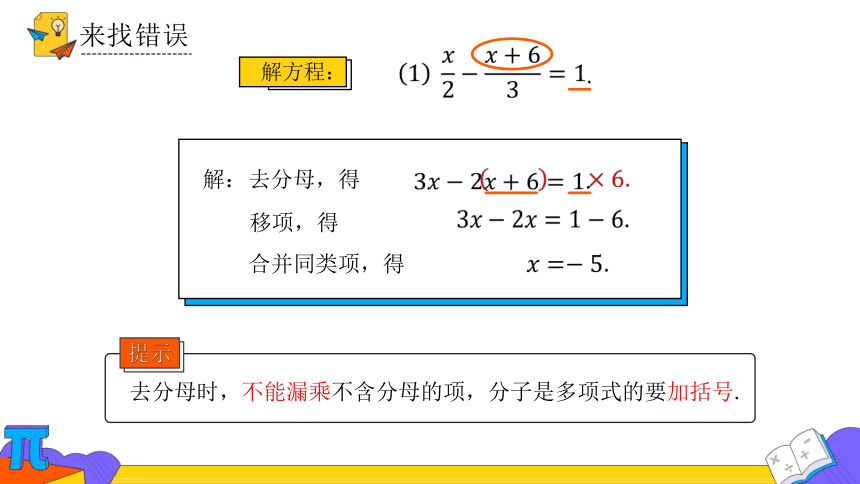
来找错误
解方程:
.
解:
去分母,得
.
移项,得
.
合并同类项,得
去分母时,不能漏乘不含分母的项,分子是多项式的要加括号.
提示
来找错误
解方程:
.
解:
去分母(两边同乘 ),得
.
移项,得
.
合并同类项,得
正确解法
去括号,得
.
.
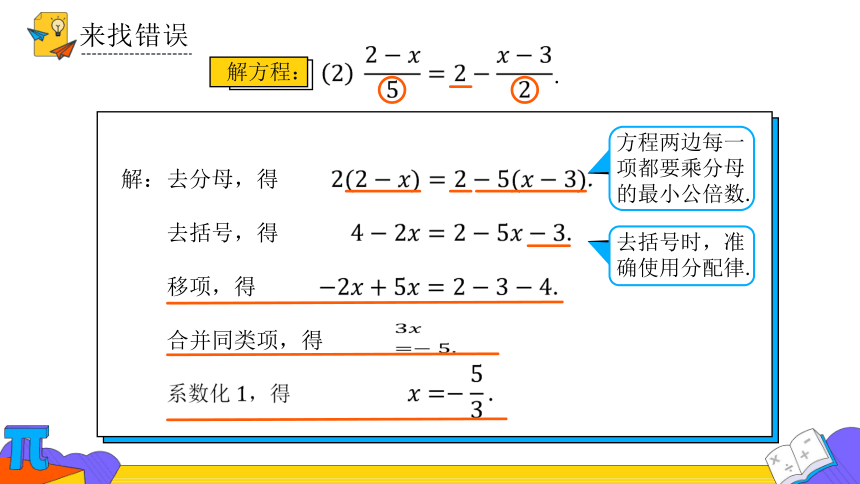
来找错误
解方程:
.
解:
去分母,得
.
移项,得
.
去括号,得
合并同类项,得
系数化,得
去括号时,准确使用分配律.
方程两边每一项都要乘分母的最小公倍数.
来找错误
解:
去分母,得
移项,得
.
合并同类项,得
正确解法
去括号,得
.
解方程:
.
系数化,得
.
例题讲解
的倍与 之和的二分之一等于
分析:
例1
例题讲解
去分母,得
移项,得
去括号,得
合并同类项,得
系数化 ,得
解:
例题讲解
有一些相同的房间需要粉刷墙面. 一天 名一级技工粉刷 个房间,结果其中有 墙面未来得及粉刷;同样时间内 名二级技工粉刷了 个房间之外,还多粉刷了另外的 墙面. 每名一级技工比二级技工一天多粉刷 墙面,求每个房间需要粉刷的墙面面积.
分析:
解:设每个房间需要粉刷的墙面面积为 .
例2
例题讲解
有一些相同的房间需要粉刷墙面. 一天 名一级技工粉刷 个房间,结果其中有 墙面未来得及粉刷;同样时间内 名二级技工粉刷了 个房间之外,还多粉刷了另外的 墙面. 每名一级技工比二级技工一天多粉刷 墙面,求每个房间需要粉刷的墙面面积.
分析:
一天的总量 每名技工的量
一级技工
二级技工
例2
例题讲解
解:设每个房间需要粉刷的墙面面积为 .
去分母,得
移项,得
去括号,得
合并同类项,得
系数化 ,得
答:每个房间需要粉刷的墙面面积为 .
一、
解一元一次方程的步骤及注意事项:
课
堂
小
结
去分母
去括号
移项
合并同类项
1
2
3
4
系数化
5
——不漏乘、分子加括号.
——不漏乘,符号问题.
——改变符号.
——系数相加减.
——分子、分母勿写反.
二、
列方程解一元一次方程应用题的步骤
课
堂
小
结
审——读题,圈画重点语句.
设——选择合适的未知量设为未知数.
列——依据等量关系列出方程.
解——采取最优步骤方案求解.
1
2
3
4
验——验证是否符合实际问题.
5
答——勿忘答题,要叙述完整,若有单位,
6
同时要写上单位.
再 见
(第四课时)
解一元一次方程(二)
复习巩固
解方程:
解:
去分母(方程两边乘 ),得
.
去括号,得
.
移项,得
系数化,得
.
合并同类项,得
.
去括号,得
移项,得
系数化,得
合并同类项,得
不漏乘、
分子加括号.
不漏乘、变号.
分子、分母勿颠倒.
向 转化
“”
来找错误
解方程:
.
解:
去分母,得
.
移项,得
.
合并同类项,得
去分母时,不能漏乘不含分母的项,分子是多项式的要加括号.
提示
来找错误
解方程:
.
解:
去分母(两边同乘 ),得
.
移项,得
.
合并同类项,得
正确解法
去括号,得
.
.
来找错误
解方程:
.
解:
去分母,得
.
移项,得
.
去括号,得
合并同类项,得
系数化,得
去括号时,准确使用分配律.
方程两边每一项都要乘分母的最小公倍数.
来找错误
解:
去分母,得
移项,得
.
合并同类项,得
正确解法
去括号,得
.
解方程:
.
系数化,得
.
例题讲解
的倍与 之和的二分之一等于
分析:
例1
例题讲解
去分母,得
移项,得
去括号,得
合并同类项,得
系数化 ,得
解:
例题讲解
有一些相同的房间需要粉刷墙面. 一天 名一级技工粉刷 个房间,结果其中有 墙面未来得及粉刷;同样时间内 名二级技工粉刷了 个房间之外,还多粉刷了另外的 墙面. 每名一级技工比二级技工一天多粉刷 墙面,求每个房间需要粉刷的墙面面积.
分析:
解:设每个房间需要粉刷的墙面面积为 .
例2
例题讲解
有一些相同的房间需要粉刷墙面. 一天 名一级技工粉刷 个房间,结果其中有 墙面未来得及粉刷;同样时间内 名二级技工粉刷了 个房间之外,还多粉刷了另外的 墙面. 每名一级技工比二级技工一天多粉刷 墙面,求每个房间需要粉刷的墙面面积.
分析:
一天的总量 每名技工的量
一级技工
二级技工
例2
例题讲解
解:设每个房间需要粉刷的墙面面积为 .
去分母,得
移项,得
去括号,得
合并同类项,得
系数化 ,得
答:每个房间需要粉刷的墙面面积为 .
一、
解一元一次方程的步骤及注意事项:
课
堂
小
结
去分母
去括号
移项
合并同类项
1
2
3
4
系数化
5
——不漏乘、分子加括号.
——不漏乘,符号问题.
——改变符号.
——系数相加减.
——分子、分母勿写反.
二、
列方程解一元一次方程应用题的步骤
课
堂
小
结
审——读题,圈画重点语句.
设——选择合适的未知量设为未知数.
列——依据等量关系列出方程.
解——采取最优步骤方案求解.
1
2
3
4
验——验证是否符合实际问题.
5
答——勿忘答题,要叙述完整,若有单位,
6
同时要写上单位.
再 见
