3.2.4 解一元一次方程(一)——合并同类项与移项 课件(共23张PPT)
文档属性
| 名称 | 3.2.4 解一元一次方程(一)——合并同类项与移项 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-26 20:38:06 | ||
图片预览







文档简介
(共23张PPT)
(第四课时)
解一元一次方程(一)
复习回顾
通过移项这个变形过程,将所给方程中含有未知数的项和常数项分别移到方程的两侧. 然后,通过合并同类项和系数化为等步骤,将方程变形为的形式,得到方程的解.
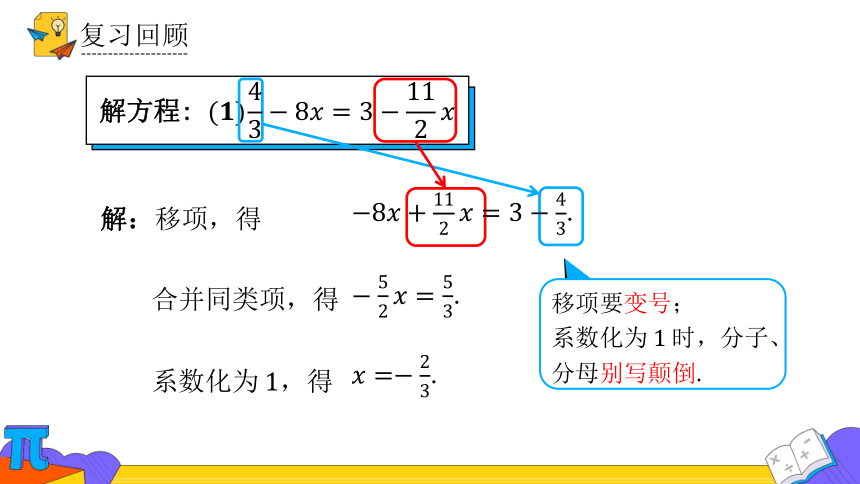
复习回顾
解方程:
解:移项,得
同类项,得
系数化为,得
移项要变号;
系数化为时,分子、分母别写颠倒.
.
.
.
复习回顾
解法一:移项,得
同类项,得.
系数化为,得.
未知数是
注意
解方程:
.
复习回顾
解法二:移项,得.
一般把未知数放在等号左边
注意
同类项,得.
系数化为,得.
即.
解方程:
复习回顾
解:移项,得
同类项,得
系数化为,得
.
.
.
解方程:
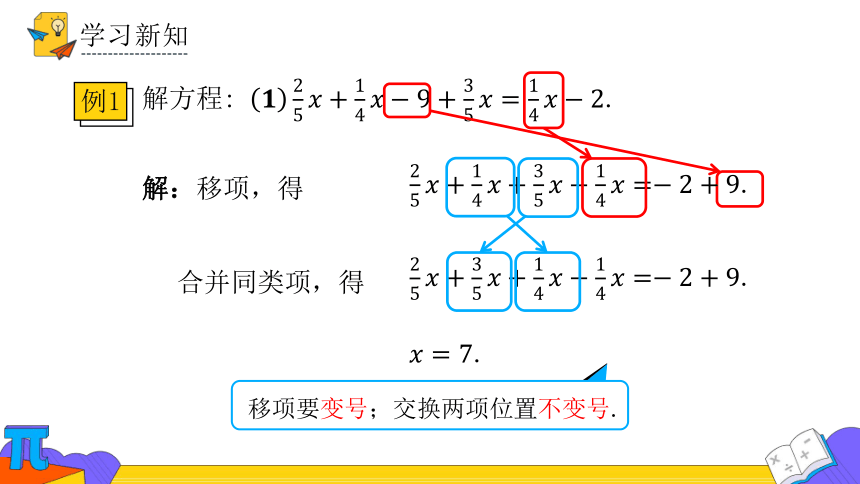
学习新知
例1
解方程: .
解:移项,得
同类项,得
.
.
.
移项要变号;
学习新知
例1
解方程: .
解:移项,得
同类项,得
.
.
.
移项要变号;
学习新知
例1
解方程: .
解:移项,得
同类项,得
.
.
.
移项要变号;交换两项位置不变号.
学习新知
例1
解方程: .
解法一:移项,得
同类项,得
.
.
.
系数化为,得
学习新知
例1
解方程: .
解法二:合并同类项,得
同类项,得
.
.
.
系数化为,得
移项,得
.
学习新知
例2
我们知道分数写为小数形式即,反过来,无限循环小数写为分数形式即 .
一般地,任何一个无限循环小数都可以写为分数形式吗?
如果可以,应怎样写呢?
设,
分析
学习新知
如何把化为分数形式?
解:设,
···
···
.
解.
所以.
只能构造倍关系吗
①
②
学习新知
如何把化为分数形式?
设,
···
···
分析
学习新知
如何把化为分数形式?
设,
···
···
所以.
解.
所以.
分析
如何将化为分数形式?
巩固练习
如何把化为分数形式?
解:设,
···
···
.
解.
所以.
①
②
巩固练习
如何把化为分数形式?
解:设,
···
···
所以.
解.
所以.
如何将
化为分数形式?
①
②
巩固练习
如何把化为分数形式?
解:设,
···
···
所以.
解.
所以.
①
②
课
堂
小
结
1
解方程移项要变号;
2
灵活利用解方程的步骤求解项数较多的一元一次方程;
课
堂
小
结
灵活利用解方程的步骤求解项数较多的一元一次方程;
2
如,解方程: .
解:合并同类项,得
.
同类项,得
.
.
系数化为,得
移项,得
.
课
堂
小
结
会用一元一次方程解决无限循环小数化分数问题.
3
如:把化为分数形式.
解:设,
···
···
.
解.
所以.
①
②
课后思考
如何把化为分数形式?
再 见
(第四课时)
解一元一次方程(一)
复习回顾
通过移项这个变形过程,将所给方程中含有未知数的项和常数项分别移到方程的两侧. 然后,通过合并同类项和系数化为等步骤,将方程变形为的形式,得到方程的解.
复习回顾
解方程:
解:移项,得
同类项,得
系数化为,得
移项要变号;
系数化为时,分子、分母别写颠倒.
.
.
.
复习回顾
解法一:移项,得
同类项,得.
系数化为,得.
未知数是
注意
解方程:
.
复习回顾
解法二:移项,得.
一般把未知数放在等号左边
注意
同类项,得.
系数化为,得.
即.
解方程:
复习回顾
解:移项,得
同类项,得
系数化为,得
.
.
.
解方程:
学习新知
例1
解方程: .
解:移项,得
同类项,得
.
.
.
移项要变号;
学习新知
例1
解方程: .
解:移项,得
同类项,得
.
.
.
移项要变号;
学习新知
例1
解方程: .
解:移项,得
同类项,得
.
.
.
移项要变号;交换两项位置不变号.
学习新知
例1
解方程: .
解法一:移项,得
同类项,得
.
.
.
系数化为,得
学习新知
例1
解方程: .
解法二:合并同类项,得
同类项,得
.
.
.
系数化为,得
移项,得
.
学习新知
例2
我们知道分数写为小数形式即,反过来,无限循环小数写为分数形式即 .
一般地,任何一个无限循环小数都可以写为分数形式吗?
如果可以,应怎样写呢?
设,
分析
学习新知
如何把化为分数形式?
解:设,
···
···
.
解.
所以.
只能构造倍关系吗
①
②
学习新知
如何把化为分数形式?
设,
···
···
分析
学习新知
如何把化为分数形式?
设,
···
···
所以.
解.
所以.
分析
如何将化为分数形式?
巩固练习
如何把化为分数形式?
解:设,
···
···
.
解.
所以.
①
②
巩固练习
如何把化为分数形式?
解:设,
···
···
所以.
解.
所以.
如何将
化为分数形式?
①
②
巩固练习
如何把化为分数形式?
解:设,
···
···
所以.
解.
所以.
①
②
课
堂
小
结
1
解方程移项要变号;
2
灵活利用解方程的步骤求解项数较多的一元一次方程;
课
堂
小
结
灵活利用解方程的步骤求解项数较多的一元一次方程;
2
如,解方程: .
解:合并同类项,得
.
同类项,得
.
.
系数化为,得
移项,得
.
课
堂
小
结
会用一元一次方程解决无限循环小数化分数问题.
3
如:把化为分数形式.
解:设,
···
···
.
解.
所以.
①
②
课后思考
如何把化为分数形式?
再 见
