4.1.2 无理数指数幂及其运算性质 课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共18张PPT)
文档属性
| 名称 | 4.1.2 无理数指数幂及其运算性质 课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 16:52:25 | ||
图片预览






文档简介
§4.1.2 无理数指数幂及其运算性质
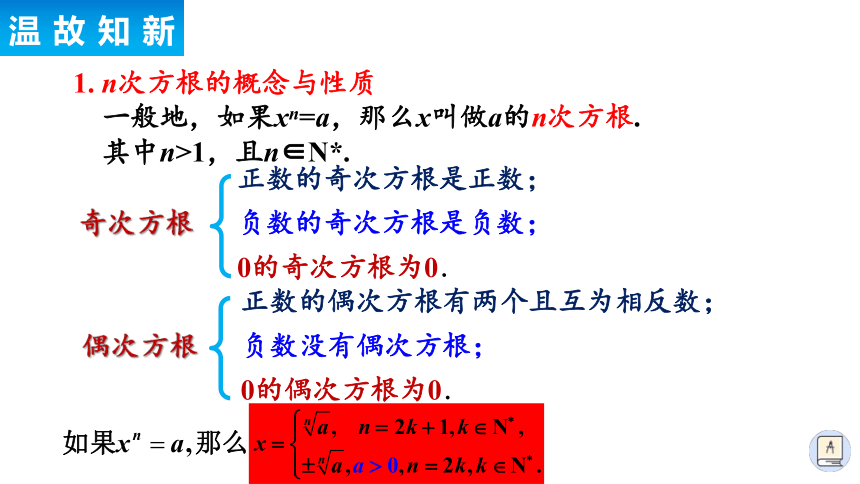
1. n次方根的概念与性质
偶次方根
负数没有偶次方根;
正数的偶次方根有两个且互为相反数;
0的偶次方根为0.
奇次方根
负数的奇次方根是负数;
正数的奇次方根是正数;
0的奇次方根为0.
温故知新
一般地,如果xn=a,那么x叫做a的n次方根.
其中n>1,且n∈N*.
2.根式的概念与性质
温故知新
性质2:当n为奇数时,????????????=????;
当n为偶数时,
?
性质1:????????????=????
?
式子????????叫做根式,其中n叫做根指数,a叫做被开方数.
?
????????????=????=????,????≥????,?????,?????
(3)规定: 0的正分数指数幂为0
0的负分数指数幂没有意义.
(1).正数的正分数指数幂的意义:
(2)正数的负分数指数幂的意义:
3.分数指数幂的意义
温故知新
4.有理指数幂的运算性质
指数的概念从整数指数推广到了有理数指数,
整数指数幂的运算性质对于有理指数幂都适用.
温故知新
上面我们将 中指数x的取值范围从整数拓展到了有理数.那么,当指数x是无理数时, 的意义是什么?它是一个确定的数吗?如果是,那么它有什么运算性质?
创设情境
网络上盛极一时的数学恒等式“1.0130≈1.35 , 1.01365≈37.8 , 1.01730≈1427.6 ”
?
形象地向我们展示了通过努力每天进步1% ,就会在一个月、一年以及两年后产生巨大差异.虽然这是一种理想化的算法,但它也让我们直观地感受到了“小小的改变和时间累积的力量”.
?
1.了解指数幂由有理数扩充到无理数的过程,理解无理数指数幂的含义.(数学抽象)
2.理解指数幂的运算性质.(数学运算)
3.能进行指数幂(实数幂)的运算.(数学运算)
学习目标
问题1 根据2的不足近似值????和过剩近似值????,利用计算工具计算相应的5????,5????的近似值并填入表中,观察它们的变化趋势,你有什么发现?
?
不足近似值:舍而不进,按照所需要的精确度截取指定数位后,直接略去后面的数位,这样就得到了一个小于真实值的近似值,叫做不足近似值;
在初中的学习中,我们通过有理数认识了一些无理数. 类似地,也可以通过有理数指数幂来认识无理数指数幂.
探究新知
过剩近似值:进一而舍,按照所需要的精确度截取指定数位后,不管去掉部分最高位是否四舍五入而全都进位,即保留部分的最后一位数加1,这样就得到一个大于真实值的近似值,叫做过剩近似值.
问题1 根据2的不足近似值????和过剩近似值????,利用计算工具计算相应的5????,5????的近似值并填入表中,观察它们的变化趋势,你有什么发现?
?
探究新知
目录
CONTENT
问题1 根据2的不足近似值????和过剩近似值????,利用计算工具计算相应的5????,5????的近似值并填入表中,观察它们的变化趋势,你有什么发现?
?
探究新知
可以发现,当 的不足近似值 x 和过剩近似值 y 逐渐逼近 时, 都趋向于同一个数,这个数就是 . 也就是说, 是一串逐渐增大的有理数指数幂
和另一串逐渐减小的有理数指数幂
逐步逼近的结果,它是一个确定的实数. 这个过程可以用图4.1-1表示 .
图4.1-1
探究新知
通过观察,可以发现:
?????2?????
5??????????5????
A是一个确定的数,就是52
?
问题2 参照以上过程,你能再给出一个无理数指数幂,如 ,说明它也是一个确定的实数吗?
(1)当 的不足近似值从小于 的方向逼近 时, 的近似值从小于 的方向逼近于同一个常数;
(2)当 的过剩近似值从大于 的方向逼近 时, 的近似值从大于 的方向逼近于同一个常数.
观察可发现 是一个确定的实数
总结
(1)无理数可以作为指数;
(2)无理数指数幂的近似值可以利用逼近的方式得到.
探究新知
一般地,无理数指数幂 是一个确定的实数. 这样,我们就将指数幂数 中指数 x 的取值范围从整数逐步拓展到了实数。实数指数幂是一个确定的实数.
二、实数指数幂的运算性质
整数指数幂的运算性质也适用于实数指数幂,即对于任意实数r,s,均有下面的运算性质.
探究新知
一、无理数指数幂
1. 计算下列各式:
解:
课堂练习
利用计算工具,探究下列实数指数幂的变化规律:
(1)x 取负实数,使得 |x| 的值逐渐增大并趋向于无穷大,计算相应的 的值,观察变化趋势;
(2)x 取正实数,使得 x 的值逐渐增大并趋向于无穷大,计算相应的 的值,观察变化趋势.
解:(1)
由此可以看出,x 取负实数,使得 |x| 的值逐渐增大并趋向于无穷大时, 趋向于0.
课堂练习
解:(2)
由此可以看出,x 取正实数,使得 x 的值逐渐增大,当 x 的值趋向于无穷大时, 的值趋向于0.
课堂练习
课堂小结
1.本节课我们学习了哪些知识?
实数指数幂
逼近思想及用有理数近似表示无理数的方法
2.思想、方法?
课后作业
1.课本109页
2.练习册4.1.2
1. n次方根的概念与性质
偶次方根
负数没有偶次方根;
正数的偶次方根有两个且互为相反数;
0的偶次方根为0.
奇次方根
负数的奇次方根是负数;
正数的奇次方根是正数;
0的奇次方根为0.
温故知新
一般地,如果xn=a,那么x叫做a的n次方根.
其中n>1,且n∈N*.
2.根式的概念与性质
温故知新
性质2:当n为奇数时,????????????=????;
当n为偶数时,
?
性质1:????????????=????
?
式子????????叫做根式,其中n叫做根指数,a叫做被开方数.
?
????????????=????=????,????≥????,?????,?????
(3)规定: 0的正分数指数幂为0
0的负分数指数幂没有意义.
(1).正数的正分数指数幂的意义:
(2)正数的负分数指数幂的意义:
3.分数指数幂的意义
温故知新
4.有理指数幂的运算性质
指数的概念从整数指数推广到了有理数指数,
整数指数幂的运算性质对于有理指数幂都适用.
温故知新
上面我们将 中指数x的取值范围从整数拓展到了有理数.那么,当指数x是无理数时, 的意义是什么?它是一个确定的数吗?如果是,那么它有什么运算性质?
创设情境
网络上盛极一时的数学恒等式“
?
形象地向我们展示了通过努力每天进步
?
1.了解指数幂由有理数扩充到无理数的过程,理解无理数指数幂的含义.(数学抽象)
2.理解指数幂的运算性质.(数学运算)
3.能进行指数幂(实数幂)的运算.(数学运算)
学习目标
问题1 根据2的不足近似值????和过剩近似值????,利用计算工具计算相应的5????,5????的近似值并填入表中,观察它们的变化趋势,你有什么发现?
?
不足近似值:舍而不进,按照所需要的精确度截取指定数位后,直接略去后面的数位,这样就得到了一个小于真实值的近似值,叫做不足近似值;
在初中的学习中,我们通过有理数认识了一些无理数. 类似地,也可以通过有理数指数幂来认识无理数指数幂.
探究新知
过剩近似值:进一而舍,按照所需要的精确度截取指定数位后,不管去掉部分最高位是否四舍五入而全都进位,即保留部分的最后一位数加1,这样就得到一个大于真实值的近似值,叫做过剩近似值.
问题1 根据2的不足近似值????和过剩近似值????,利用计算工具计算相应的5????,5????的近似值并填入表中,观察它们的变化趋势,你有什么发现?
?
探究新知
目录
CONTENT
问题1 根据2的不足近似值????和过剩近似值????,利用计算工具计算相应的5????,5????的近似值并填入表中,观察它们的变化趋势,你有什么发现?
?
探究新知
可以发现,当 的不足近似值 x 和过剩近似值 y 逐渐逼近 时, 都趋向于同一个数,这个数就是 . 也就是说, 是一串逐渐增大的有理数指数幂
和另一串逐渐减小的有理数指数幂
逐步逼近的结果,它是一个确定的实数. 这个过程可以用图4.1-1表示 .
图4.1-1
探究新知
通过观察,可以发现:
?????2?????
5??????????5????
A是一个确定的数,就是52
?
问题2 参照以上过程,你能再给出一个无理数指数幂,如 ,说明它也是一个确定的实数吗?
(1)当 的不足近似值从小于 的方向逼近 时, 的近似值从小于 的方向逼近于同一个常数;
(2)当 的过剩近似值从大于 的方向逼近 时, 的近似值从大于 的方向逼近于同一个常数.
观察可发现 是一个确定的实数
总结
(1)无理数可以作为指数;
(2)无理数指数幂的近似值可以利用逼近的方式得到.
探究新知
一般地,无理数指数幂 是一个确定的实数. 这样,我们就将指数幂数 中指数 x 的取值范围从整数逐步拓展到了实数。实数指数幂是一个确定的实数.
二、实数指数幂的运算性质
整数指数幂的运算性质也适用于实数指数幂,即对于任意实数r,s,均有下面的运算性质.
探究新知
一、无理数指数幂
1. 计算下列各式:
解:
课堂练习
利用计算工具,探究下列实数指数幂的变化规律:
(1)x 取负实数,使得 |x| 的值逐渐增大并趋向于无穷大,计算相应的 的值,观察变化趋势;
(2)x 取正实数,使得 x 的值逐渐增大并趋向于无穷大,计算相应的 的值,观察变化趋势.
解:(1)
由此可以看出,x 取负实数,使得 |x| 的值逐渐增大并趋向于无穷大时, 趋向于0.
课堂练习
解:(2)
由此可以看出,x 取正实数,使得 x 的值逐渐增大,当 x 的值趋向于无穷大时, 的值趋向于0.
课堂练习
课堂小结
1.本节课我们学习了哪些知识?
实数指数幂
逼近思想及用有理数近似表示无理数的方法
2.思想、方法?
课后作业
1.课本109页
2.练习册4.1.2
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
