4.2.1 等差数列的概念(第1课时 等差数列的概念及通项公式)课件-2022-2023学年高二上学期数学人教A版(2019)选择性必修第二册(共32张PPT)
文档属性
| 名称 | 4.2.1 等差数列的概念(第1课时 等差数列的概念及通项公式)课件-2022-2023学年高二上学期数学人教A版(2019)选择性必修第二册(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 16:53:34 | ||
图片预览











文档简介
(共32张PPT)
高中数学(选择性必修) 第二册
第一课时 等差数列的概念及通项公式
4.2 等差数列
2022.11.22
1
4.2.1 等差数列的概念
教学目标
通过对数列概念的探究,培养学生严谨求实的学习作风和锲而不舍的学习精神,养成细心观察、认真分析、善于总结的良好学习习惯.
知识与技能:
过程与方法:
通过对数列概念的探究,培养学生观察、归纳、 类比、猜想、推理等发现规律的一般方法。通过阶梯性练习,提高学生的分析问题和解决问题的能力.
情感态度与价值观:
1.正确理解等差数列的概念;
2.掌握等差数列的通项公式;
3、并能对等差数列的通项公式进行简单的运用.
2
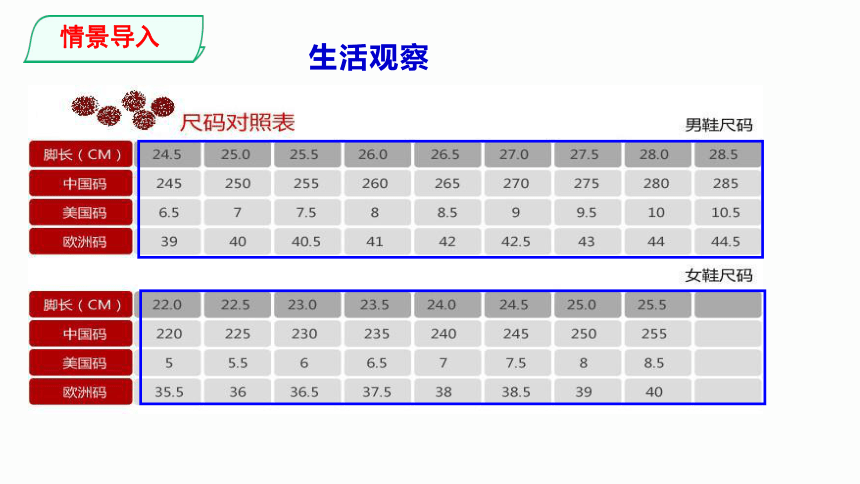
生活观察
情景导入
我们知道,数列是一种特殊的函数. 在函数的研究中,我们在理解了函数的一般概念,了解了函数变化规律的研究内容(如单调性、奇偶性)后,通过研究基本初等函数,不仅加深了对函数的理解,而且掌握了幂函数、指数函数、对数函数、三角函数等非常有用的函数模型.
类似地,在了解了数列的一般概念后,我们要研究一些具有特殊变化规律的数列,建立它们的通项公式和前n项和公式,并运用它们解决实际问题和数学问题,从中感受数学模型的现实意义与应用. 下面,我们从一类取值规律比较简单的数列入手.
4.2 等 差 数 列
2. S, M, L, XL, XXL, XXXL型号的女装上衣对应的尺码分别是
38 , 40 , 42 , 44 , 46 , 48. (2)
1 .北京天坛圜丘坛的地面由石板铺成, 最中间是圆形的天心石, 围绕天心石的是9圈扇环形的石板, 从内到外各圈的石板数依次为
9, 18, 27, 36, 45, 54, 63, 72, 81. (1)
3.测量某地垂直地面方向上海拔500米以下的大气温度, 得到从距离地面20米起每升高100米处的大气温度(单位: C)依次为
25 , 24 , 23 , 22 , 21. (3)
请看下面几个问题中的数列.
导入新课:
5
思考p13:在代数的学习中,我们常常通过运算来发现规律. 例如,在指数函数的学习中,我们通过运算发现了A、B两地旅游人数的变化规律,类似的,你能通过运算发现以上数列的取值规律吗?
6
9 , 18 , 27 , 36 , 45 , 54 , 63 , 72 , 81.
38 , 40 , 42 , 44 , 46 , 48.
(3) 25 , 24 , 23 , 22 , 21.
对于①,我们发现 18=9+9 , 27=18+9 , .... , 81=72+9,
换一种写法,就是 18-9=9 , 27-18=9 , .... , 81-72=9.
如果用{an}表示数列①, 那么有a2-a1=9 , a3- a2 =9 , ... , a9-a8=9.
这表明,数列①有这样的取值规律:从第2项起,每一项与 它的前一项的差都等于同一个常数.
同样:数列(2)、(3)
也有这样的取值规律.
(1)姚明刚进NBA一周训练罚球个数:
6000, 6500, 7000, 7500, 8000, 8500,( )
(2)某女鞋的尺码(鞋底长,单位CM):
22.5, 23, 23.5, 24, 24.5, 25, 25.5,( )
(3)某系统抽样所抽取的样本号分别是:
115,103,91,79,67,55,( ) .
(4) 8, 8, 8, 8,( )
9000
26
43
8
1、观察下列数列并按规律填空,以下四组数据有什么共同特点?
结论:同一组数列中从第二项起,每一项与前一项的差是同一个常数.
相差500
相差0.5
相差-12
相差 0
导入新课:
7
新课讲授:一、等差数列及其有关概念
2、等差数列的符号表示(定义式)
1、等差数列的定义:
数列{an}中,任取连续的两项 an、an-1 (n≥2) 或 an+1、an (n∈ N*).
若 an-an-1=d (常数) (n≥2) {an}为等差数列.
如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列。
这个常数叫做等差数列的公差,通常用字母d表示。
或: 若an+1-an= d(常数) (n∈ N*) {an}为等差数列
8
9
(1)姚明刚进NBA一周训练罚球个数:
6000, 6500, 7000, 7500, 8000, 8500,( )
(2)某女鞋的尺码(鞋底长,单位CM):
22.5, 23, 23.5, 24, 24.5, 25, 25.5,( )
(3)某系统抽样所抽取的样本号分别是:
115,103,91,79,67,55,( ) .
(4) 8, 8, 8, 8,( )
8
1、观察下列数列并按规律填空,它们的共同特点是什么?
d =500
上述数列的共同特征:从第二项起每一项与前一项的差是同一个常数.
d = -12
43
9000
26
d = 0.5
d = 0
10
导入新课:
(2)若一个数列从第2项起每一项与它前一项的差都是常数 ,
则这个数列一定是等差数列. ( )
(1)若某数列中的各项依次为16, 32, 48, 64, 80, 96, 112, 128, …,
则该数列为等差数列. ( )
√
×
√
判断正误.(请在括号中打“√”或“×”)
(3) 若a,b,c是等差数列,则c,b,a也是等差数列. ( )
11
课堂练习:1
解析 :比如 1, 2, 4, 7, 11, 16, … 不是等差数列
例1、判断下列数列是否是等差数列
① 15,12,10,8,6…( ) ④ 1,3,6,10,15… ( )
② 4,7,10,13,16… ( ) ⑤ 6,4,2,0,-2… ( )
③ a,a,a,a,a,… ( ) ⑥ 5,5,5,5,5…( )
分析:判断等差数列的方法:定义法
an+1-an=d(常数) {an}是等差数列 ;
×
×
注意
①公差是每一项(第2项起)与它的前一项的差;
②差值d要求是同一个常数;公差d可以是正数,负数,也可以为0;
12
典型例题:
1、判定下列数列是否是等差数列? 如果是,请说明公差?
(1)4 ,5,6,7,8,…; ( )
(2)1,1,1,1 ,1,…; ( )
(3)5,3,1,-1,-3,…; ( )
(4)1,2,3,2,3,4,…;( )
(5) 0,2,3,4,5,6,… . ( )
对点练清:1
d=1
d=0
d= -2
×
×
>0,递增数列
= 0,常数列
< 0,递减数列
13
分析:判断等差数列的方法:定义法
an+1-an=d(常数) {an}是等差数列 ;
例2、已知数列{an},a1 = -2,an+1 =an +3,
(1)试写出这个数列的第2项到第5项;
(2)判断该数列是否为等差数列.
解:(1)数列{an}中,
a1 = -2,an+1 =an +3
∴a2= a1+3= -2+3=1 ;
a3= a2+3= 1+3=4 ;
a4= a3+3= 4+3=7 ;
a5= a4+3= 7+3=10.
(2)数列{an}中,an+1 =an +3
∴an+1 -an =3 定值
数列{an}为等差数列.
分析:判断等差数列的方法:定义法
an+1-an=d (常数) {an}是等差数列 ;
典型例题:
14
1、已知等差数列的首项为12,公差为-5,试写出该数列的第2项到第5项.
等差数列{an}中,a1= 12
解:设该等差数列为{an},
则 a1=12,公差d = -5 ;
∴a2= a1+d= 12+(-5)=7 ;
a3= a2+d= 7+(-5)=2 ;
a4= a3+d= 2+(-5)=-3 ;
a5= a4+d= -3+(-5)=-8.
分析:根据等差数列的定义可知:
an+1=an+d (常数)
课堂练习:3
如果在a与b中间插入一个数 A,使 a, A, b成等差数列, 那么A应满足什么条件?
例3、在下列的两个数中插入一个数使它们成等差数列.
(1) 3、( )、7; (2) -12,( )、0.
思考:
解析:由a, A, b成等差数列可知:A-a = b-A
反过来,
a+b = 2A a, A, b 成等差数列
-6
5
16
典型例题:
2、等差中项:
如果a, A, b成等差数列,那么A叫做a与b的等差中项.
17
新课讲授:一、等差数列及其有关概念
-8
因为 an+1-an = d ,
所以 a2-a1=d,a3-a2=d,a4-a3=d,… …
则 a2=a1+d ,
a3 = a2+d = (a1+d )+d = a1+2d ,
a4=a3+d=(a1+2d )+d = a1+3d ,
归纳可得 an=an-1+d=a1+(n-1)d (n ≥ 2)
当 n=1时,上式为a1= a1 +(1-1) d = a1 . 这就是说 , 上式当n=1也成立.
因此:等差数列{an}的通项公式为:
an=a1+(n-1)d
递推公式
已知等差数列{an} ,它的公差是d,求{an}的通项公式 .
方法1:
探究 p13:你能根据等差数列的定义推导它的通项公式吗?
不完全归纳法
18
由等差数列的定义:an-an-1=d
(n-1)个
因此:a2-a1=d
a3-a2=d
a4-a3=d
…
an-1-an-2=d
an-an-1=d
将所有等式相加得
n=1时亦成立
an-a1=(n-1)d
方法2:
an=a1+(n-1)d
探究 p13:你能根据等差数列的定义推导它的通项公式吗?
已知等差数列{an} ,它的公差是d,求{an}的通项公式 .
累加法
19
1、递推公式: an+1-an = d ,
2、通项公式为:
an=a1+(n-1) d
已知等差数列{an} , 首项 a1,公差是d,求{an}的通项公式 .
an、a1、n、d
知三求一
新课讲授:二、等差数列的通项公式
20
思考p14:观察等差数列{an}的通项公式 , 你认为它与我们
熟悉的哪一类函数有关
由于an=a1+(n-1)d =dn+(a1-d),
如图:在平面直角坐标中画出函数
f(x)=dx+(a1-d) 的图像,
就得到一条斜率为d, 截距为a1-d的直线.
an=f (n)
∴当d≠0时 , an是一次函数 f(x)=dx+(a1-d)
(x∈R)当x=n时的函数值 , 即
新课讲授:二、等差数列的通项公式
21
在这条直线上描出点
(1 , f(1)) , (2, f(2)) , , (n, f(n)) , ,
就得到等差数列an的图像.
事实上, 公差d≠0的等差数列{an} 的图象是
点(n, an)组成的集合, 这些点均匀分布在
直线 f(x)=dx+(a1-d)上面.
反之, 任给一次函数f(x)=kx+b (k和b为常数),
则f(1)=k+b, f(2)=2k+b, , f(n)=nk+b, ,
构成一个等差数列{nk+b}, 其首项为(k+b), 公差为k.
新课讲授:二、等差数列的通项公式
22
例1.已知数列{an}的通项公式是an=3n-1,求证:{an}为等差数列.
证明:数列{an}中,an=3n-1,
∴an+1=3(n+1)-1
∴an+1-an=[3(n+1)-1]-(3n-1)
=(3n+2)-(3n-1)=3
∴{an}为等差数列。
分析:判断等差数列的方法:(定义法)
an+1-an=d {an}是等差数列
小结:等差数列的判定与证明:
(1)等差数列的判定方法: (定义法)
an+1-an= d (常数) ( n∈N* )
{an}为等差数列;
(2) 要证明一个数列是等差数列,
一般用定义法 .
典型例题 :
23
(1) an=2n-3 ( );
(2) an=n2-1 ( ) ;
(3) an=5-3n ( ) ;
(4) an=7n+3 ( ).
课堂练习:1
1、已知数列{an},判断下列数列是否为等差数列?
分析:1°等差数列的判定方法:(定义法)
an+1-an= d (常数 ) ( n∈N* ) {an}为等差数列.
×
d = an+1- an=7
d = an+1- an=2
d = an+1- an=-3
d = an+1- an=2n+1
不确定
常数
常数
常数
2°类似 an=kn+b 形式是等差数列.
24
例2 已知等差数列{an}的通项公式为an=5-2n,求数列{an}的公差和首项;
解: 当n≥2时,由{an}的通项公式 an = 5-2n ,
可得: an-1 =5-2(n-1)=7-2n ,
∴公差 d=an-an-1 = (5-2n )–(7-2n )= -2,
典型例题 p14:
把 n = 1代入 an = 5-2n, 得 a1=5-2×1=3.
所以 {an}的公差为-2 , 首项为 3.
分析:已知等差数列的通项公式,只要根据等差数列的定义,
由 an+1-an = d ,即可求出公差d ;
25
解: 由已知条件, 得d =5-8=-3.
把 a1= 8 , d =-3代入an=a1+(n-1)d , 得
an= 8-3(n-1)=11-3n.
把n=20代入上式,得 a20 = 11-3×20 =-49.
所以,这个数列的第 20 项是-49.
典型例题 p14:
例3 求等差数列8,5,2,······的第20项;
分析:可以先根据数列的两个已知项求出通项公式,
再利用通项公式求数列的第20项.
26
例4 . -401是不是等差数列-5, -9, -13,···的项?如果是, 是第几项?
分析:先求出数列的通项公式,它是一个关于n的方程,再看
-401是否能使这个方程有正整数解.
解:设等差数列为 {an} 由题意 :a1=-5,
公差 d =-9- (-5)=-4 ,
则数列{an}的通项公式为:
an=-5-4(n-1)=-4n-1.
令-4n-1=-401, 解得n=100.
所以,-401是这个数列的项,是第100项.
典型例题 p15:
27
典型例题:等差中项理解和应用
例5、已知三个数的和为18,且这三个数组成公差为3 的等差数列,求这三个数.
分析:三个数成等差数列,可采用对称的设法:a-d、a、a+d .
解:设所求三个数为:a-3、a、a+3,
由题意可知:(a-3)+a+(a+3)=18;
则 3a = 18
∴a = 6
∴所求三个为:3、6、9.
28
课堂练习:2
1、若一个三角形的三个内角成等差数列,其中一个内角为32°,
则其他两角度数为 , .
分析:隐含条件三角形内角和为180°.
解:由题意设三角形三个内角分别为:
x-d,x,x+d,
则 (x-d)+x+(x+d)=180
解得:3x=180∴x=60
又∵其中一个角为32°∴公差d=60-32=28
∴另外一个角为 x+d=88
三角形其它两角度数为:60°,88°
88°
60°
29
1. 定义: 如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列。
2. 通项公式: an=a1+(n-1)d
4. 图象:直线上均匀排开的一群孤立的点.
3. 等差中项:a, A , b成等差数列 2A=a+b.
{an}为等差数列
5. 等差数列的判断
an-an-1=d (n≥2)或an+1-an=d (n∈N*).
课堂小结
30
不渴望能够一跃千里,只希望每天能够前进一步。
31
课后作业:
再见!
32
高中数学(选择性必修) 第二册
第一课时 等差数列的概念及通项公式
4.2 等差数列
2022.11.22
1
4.2.1 等差数列的概念
教学目标
通过对数列概念的探究,培养学生严谨求实的学习作风和锲而不舍的学习精神,养成细心观察、认真分析、善于总结的良好学习习惯.
知识与技能:
过程与方法:
通过对数列概念的探究,培养学生观察、归纳、 类比、猜想、推理等发现规律的一般方法。通过阶梯性练习,提高学生的分析问题和解决问题的能力.
情感态度与价值观:
1.正确理解等差数列的概念;
2.掌握等差数列的通项公式;
3、并能对等差数列的通项公式进行简单的运用.
2
生活观察
情景导入
我们知道,数列是一种特殊的函数. 在函数的研究中,我们在理解了函数的一般概念,了解了函数变化规律的研究内容(如单调性、奇偶性)后,通过研究基本初等函数,不仅加深了对函数的理解,而且掌握了幂函数、指数函数、对数函数、三角函数等非常有用的函数模型.
类似地,在了解了数列的一般概念后,我们要研究一些具有特殊变化规律的数列,建立它们的通项公式和前n项和公式,并运用它们解决实际问题和数学问题,从中感受数学模型的现实意义与应用. 下面,我们从一类取值规律比较简单的数列入手.
4.2 等 差 数 列
2. S, M, L, XL, XXL, XXXL型号的女装上衣对应的尺码分别是
38 , 40 , 42 , 44 , 46 , 48. (2)
1 .北京天坛圜丘坛的地面由石板铺成, 最中间是圆形的天心石, 围绕天心石的是9圈扇环形的石板, 从内到外各圈的石板数依次为
9, 18, 27, 36, 45, 54, 63, 72, 81. (1)
3.测量某地垂直地面方向上海拔500米以下的大气温度, 得到从距离地面20米起每升高100米处的大气温度(单位: C)依次为
25 , 24 , 23 , 22 , 21. (3)
请看下面几个问题中的数列.
导入新课:
5
思考p13:在代数的学习中,我们常常通过运算来发现规律. 例如,在指数函数的学习中,我们通过运算发现了A、B两地旅游人数的变化规律,类似的,你能通过运算发现以上数列的取值规律吗?
6
9 , 18 , 27 , 36 , 45 , 54 , 63 , 72 , 81.
38 , 40 , 42 , 44 , 46 , 48.
(3) 25 , 24 , 23 , 22 , 21.
对于①,我们发现 18=9+9 , 27=18+9 , .... , 81=72+9,
换一种写法,就是 18-9=9 , 27-18=9 , .... , 81-72=9.
如果用{an}表示数列①, 那么有a2-a1=9 , a3- a2 =9 , ... , a9-a8=9.
这表明,数列①有这样的取值规律:从第2项起,每一项与 它的前一项的差都等于同一个常数.
同样:数列(2)、(3)
也有这样的取值规律.
(1)姚明刚进NBA一周训练罚球个数:
6000, 6500, 7000, 7500, 8000, 8500,( )
(2)某女鞋的尺码(鞋底长,单位CM):
22.5, 23, 23.5, 24, 24.5, 25, 25.5,( )
(3)某系统抽样所抽取的样本号分别是:
115,103,91,79,67,55,( ) .
(4) 8, 8, 8, 8,( )
9000
26
43
8
1、观察下列数列并按规律填空,以下四组数据有什么共同特点?
结论:同一组数列中从第二项起,每一项与前一项的差是同一个常数.
相差500
相差0.5
相差-12
相差 0
导入新课:
7
新课讲授:一、等差数列及其有关概念
2、等差数列的符号表示(定义式)
1、等差数列的定义:
数列{an}中,任取连续的两项 an、an-1 (n≥2) 或 an+1、an (n∈ N*).
若 an-an-1=d (常数) (n≥2) {an}为等差数列.
如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列。
这个常数叫做等差数列的公差,通常用字母d表示。
或: 若an+1-an= d(常数) (n∈ N*) {an}为等差数列
8
9
(1)姚明刚进NBA一周训练罚球个数:
6000, 6500, 7000, 7500, 8000, 8500,( )
(2)某女鞋的尺码(鞋底长,单位CM):
22.5, 23, 23.5, 24, 24.5, 25, 25.5,( )
(3)某系统抽样所抽取的样本号分别是:
115,103,91,79,67,55,( ) .
(4) 8, 8, 8, 8,( )
8
1、观察下列数列并按规律填空,它们的共同特点是什么?
d =500
上述数列的共同特征:从第二项起每一项与前一项的差是同一个常数.
d = -12
43
9000
26
d = 0.5
d = 0
10
导入新课:
(2)若一个数列从第2项起每一项与它前一项的差都是常数 ,
则这个数列一定是等差数列. ( )
(1)若某数列中的各项依次为16, 32, 48, 64, 80, 96, 112, 128, …,
则该数列为等差数列. ( )
√
×
√
判断正误.(请在括号中打“√”或“×”)
(3) 若a,b,c是等差数列,则c,b,a也是等差数列. ( )
11
课堂练习:1
解析 :比如 1, 2, 4, 7, 11, 16, … 不是等差数列
例1、判断下列数列是否是等差数列
① 15,12,10,8,6…( ) ④ 1,3,6,10,15… ( )
② 4,7,10,13,16… ( ) ⑤ 6,4,2,0,-2… ( )
③ a,a,a,a,a,… ( ) ⑥ 5,5,5,5,5…( )
分析:判断等差数列的方法:定义法
an+1-an=d(常数) {an}是等差数列 ;
×
×
注意
①公差是每一项(第2项起)与它的前一项的差;
②差值d要求是同一个常数;公差d可以是正数,负数,也可以为0;
12
典型例题:
1、判定下列数列是否是等差数列? 如果是,请说明公差?
(1)4 ,5,6,7,8,…; ( )
(2)1,1,1,1 ,1,…; ( )
(3)5,3,1,-1,-3,…; ( )
(4)1,2,3,2,3,4,…;( )
(5) 0,2,3,4,5,6,… . ( )
对点练清:1
d=1
d=0
d= -2
×
×
>0,递增数列
= 0,常数列
< 0,递减数列
13
分析:判断等差数列的方法:定义法
an+1-an=d(常数) {an}是等差数列 ;
例2、已知数列{an},a1 = -2,an+1 =an +3,
(1)试写出这个数列的第2项到第5项;
(2)判断该数列是否为等差数列.
解:(1)数列{an}中,
a1 = -2,an+1 =an +3
∴a2= a1+3= -2+3=1 ;
a3= a2+3= 1+3=4 ;
a4= a3+3= 4+3=7 ;
a5= a4+3= 7+3=10.
(2)数列{an}中,an+1 =an +3
∴an+1 -an =3 定值
数列{an}为等差数列.
分析:判断等差数列的方法:定义法
an+1-an=d (常数) {an}是等差数列 ;
典型例题:
14
1、已知等差数列的首项为12,公差为-5,试写出该数列的第2项到第5项.
等差数列{an}中,a1= 12
解:设该等差数列为{an},
则 a1=12,公差d = -5 ;
∴a2= a1+d= 12+(-5)=7 ;
a3= a2+d= 7+(-5)=2 ;
a4= a3+d= 2+(-5)=-3 ;
a5= a4+d= -3+(-5)=-8.
分析:根据等差数列的定义可知:
an+1=an+d (常数)
课堂练习:3
如果在a与b中间插入一个数 A,使 a, A, b成等差数列, 那么A应满足什么条件?
例3、在下列的两个数中插入一个数使它们成等差数列.
(1) 3、( )、7; (2) -12,( )、0.
思考:
解析:由a, A, b成等差数列可知:A-a = b-A
反过来,
a+b = 2A a, A, b 成等差数列
-6
5
16
典型例题:
2、等差中项:
如果a, A, b成等差数列,那么A叫做a与b的等差中项.
17
新课讲授:一、等差数列及其有关概念
-8
因为 an+1-an = d ,
所以 a2-a1=d,a3-a2=d,a4-a3=d,… …
则 a2=a1+d ,
a3 = a2+d = (a1+d )+d = a1+2d ,
a4=a3+d=(a1+2d )+d = a1+3d ,
归纳可得 an=an-1+d=a1+(n-1)d (n ≥ 2)
当 n=1时,上式为a1= a1 +(1-1) d = a1 . 这就是说 , 上式当n=1也成立.
因此:等差数列{an}的通项公式为:
an=a1+(n-1)d
递推公式
已知等差数列{an} ,它的公差是d,求{an}的通项公式 .
方法1:
探究 p13:你能根据等差数列的定义推导它的通项公式吗?
不完全归纳法
18
由等差数列的定义:an-an-1=d
(n-1)个
因此:a2-a1=d
a3-a2=d
a4-a3=d
…
an-1-an-2=d
an-an-1=d
将所有等式相加得
n=1时亦成立
an-a1=(n-1)d
方法2:
an=a1+(n-1)d
探究 p13:你能根据等差数列的定义推导它的通项公式吗?
已知等差数列{an} ,它的公差是d,求{an}的通项公式 .
累加法
19
1、递推公式: an+1-an = d ,
2、通项公式为:
an=a1+(n-1) d
已知等差数列{an} , 首项 a1,公差是d,求{an}的通项公式 .
an、a1、n、d
知三求一
新课讲授:二、等差数列的通项公式
20
思考p14:观察等差数列{an}的通项公式 , 你认为它与我们
熟悉的哪一类函数有关
由于an=a1+(n-1)d =dn+(a1-d),
如图:在平面直角坐标中画出函数
f(x)=dx+(a1-d) 的图像,
就得到一条斜率为d, 截距为a1-d的直线.
an=f (n)
∴当d≠0时 , an是一次函数 f(x)=dx+(a1-d)
(x∈R)当x=n时的函数值 , 即
新课讲授:二、等差数列的通项公式
21
在这条直线上描出点
(1 , f(1)) , (2, f(2)) , , (n, f(n)) , ,
就得到等差数列an的图像.
事实上, 公差d≠0的等差数列{an} 的图象是
点(n, an)组成的集合, 这些点均匀分布在
直线 f(x)=dx+(a1-d)上面.
反之, 任给一次函数f(x)=kx+b (k和b为常数),
则f(1)=k+b, f(2)=2k+b, , f(n)=nk+b, ,
构成一个等差数列{nk+b}, 其首项为(k+b), 公差为k.
新课讲授:二、等差数列的通项公式
22
例1.已知数列{an}的通项公式是an=3n-1,求证:{an}为等差数列.
证明:数列{an}中,an=3n-1,
∴an+1=3(n+1)-1
∴an+1-an=[3(n+1)-1]-(3n-1)
=(3n+2)-(3n-1)=3
∴{an}为等差数列。
分析:判断等差数列的方法:(定义法)
an+1-an=d {an}是等差数列
小结:等差数列的判定与证明:
(1)等差数列的判定方法: (定义法)
an+1-an= d (常数) ( n∈N* )
{an}为等差数列;
(2) 要证明一个数列是等差数列,
一般用定义法 .
典型例题 :
23
(1) an=2n-3 ( );
(2) an=n2-1 ( ) ;
(3) an=5-3n ( ) ;
(4) an=7n+3 ( ).
课堂练习:1
1、已知数列{an},判断下列数列是否为等差数列?
分析:1°等差数列的判定方法:(定义法)
an+1-an= d (常数 ) ( n∈N* ) {an}为等差数列.
×
d = an+1- an=7
d = an+1- an=2
d = an+1- an=-3
d = an+1- an=2n+1
不确定
常数
常数
常数
2°类似 an=kn+b 形式是等差数列.
24
例2 已知等差数列{an}的通项公式为an=5-2n,求数列{an}的公差和首项;
解: 当n≥2时,由{an}的通项公式 an = 5-2n ,
可得: an-1 =5-2(n-1)=7-2n ,
∴公差 d=an-an-1 = (5-2n )–(7-2n )= -2,
典型例题 p14:
把 n = 1代入 an = 5-2n, 得 a1=5-2×1=3.
所以 {an}的公差为-2 , 首项为 3.
分析:已知等差数列的通项公式,只要根据等差数列的定义,
由 an+1-an = d ,即可求出公差d ;
25
解: 由已知条件, 得d =5-8=-3.
把 a1= 8 , d =-3代入an=a1+(n-1)d , 得
an= 8-3(n-1)=11-3n.
把n=20代入上式,得 a20 = 11-3×20 =-49.
所以,这个数列的第 20 项是-49.
典型例题 p14:
例3 求等差数列8,5,2,······的第20项;
分析:可以先根据数列的两个已知项求出通项公式,
再利用通项公式求数列的第20项.
26
例4 . -401是不是等差数列-5, -9, -13,···的项?如果是, 是第几项?
分析:先求出数列的通项公式,它是一个关于n的方程,再看
-401是否能使这个方程有正整数解.
解:设等差数列为 {an} 由题意 :a1=-5,
公差 d =-9- (-5)=-4 ,
则数列{an}的通项公式为:
an=-5-4(n-1)=-4n-1.
令-4n-1=-401, 解得n=100.
所以,-401是这个数列的项,是第100项.
典型例题 p15:
27
典型例题:等差中项理解和应用
例5、已知三个数的和为18,且这三个数组成公差为3 的等差数列,求这三个数.
分析:三个数成等差数列,可采用对称的设法:a-d、a、a+d .
解:设所求三个数为:a-3、a、a+3,
由题意可知:(a-3)+a+(a+3)=18;
则 3a = 18
∴a = 6
∴所求三个为:3、6、9.
28
课堂练习:2
1、若一个三角形的三个内角成等差数列,其中一个内角为32°,
则其他两角度数为 , .
分析:隐含条件三角形内角和为180°.
解:由题意设三角形三个内角分别为:
x-d,x,x+d,
则 (x-d)+x+(x+d)=180
解得:3x=180∴x=60
又∵其中一个角为32°∴公差d=60-32=28
∴另外一个角为 x+d=88
三角形其它两角度数为:60°,88°
88°
60°
29
1. 定义: 如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列。
2. 通项公式: an=a1+(n-1)d
4. 图象:直线上均匀排开的一群孤立的点.
3. 等差中项:a, A , b成等差数列 2A=a+b.
{an}为等差数列
5. 等差数列的判断
an-an-1=d (n≥2)或an+1-an=d (n∈N*).
课堂小结
30
不渴望能够一跃千里,只希望每天能够前进一步。
31
课后作业:
再见!
32
