4.4.3 不同函数增长的差异 课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共13张PPT)
文档属性
| 名称 | 4.4.3 不同函数增长的差异 课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-25 00:00:00 | ||
图片预览





文档简介
4.4.3 不同函数增长的差异
讲课人:XX
1.理解函数模型是描述客观世界中变量关系和规律的重要工具。
2.在实际情境中,会选择合适的函数类型刻画现实问题的变化规律。
3.比较对数函数、一次函数、指数函数增长速度的差异,理解“对数增长”“直线上升”“指数爆炸”等术语的现实含义。
教学目标
重点
难点
我们学习过的一次函数、二次函数、反比例函数、幂函数、指数函数、对数函数中,哪些函数在定义域上是增函数?
问题导入
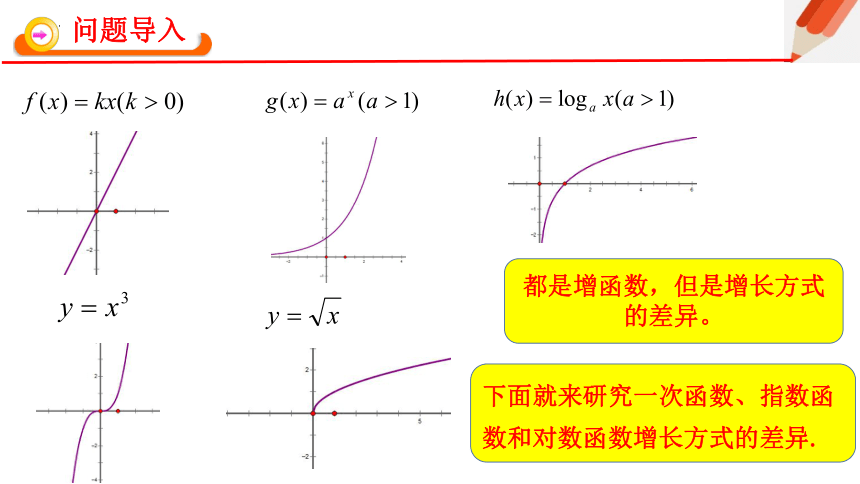
问题导入
都是增函数,但是增长方式的差异。
下面就来研究一次函数、指数函数和对数函数增长方式的差异.
探究:观察函数????=????????,????=????????,????=????????????????????,探索它们在区间[0,+∞)上的增长差异,思考以下几个问题.
?
实验探究
问题1:三个函数在区间[????,+∞)上的图象有什么特点?
?
问题2:当x趋于无穷大时,三个函数中哪个函数的增长最快?哪个最慢?
小组讨论
指数函数、一次函数与对数函数增长的差异
{EB344D84-9AFB-497E-A393-DC336BA19D2E}
指数函数
一次函数
对数函数
解析式
y=ax(a>1)
y=kx(k>0)
y=logax(a>1)
单调性
在[0,+∞)上单调递增
图象
(随x的增大)
趋向于和x轴_____
呈直线上升
趋向于和x轴_____
增长速度
(随x的增大)
y的增长速度越来越___
y的增长速度_ _
y的增长速度越来越___
归纳总结
总会存在一个x0,当x>x0时, __________
垂直
平行
快
慢
ax >kx>logax
不变
实验探究
实验探究
一般地,虽然对数函数????=????????????????????(????>????)与一次函数????=????????(????>????)在区间(????,+∞)上都单调递增,但它们的增长速度不同.
随着????的增大,一次函数????=????????(????>????)保持固定的增长速度,而对数函数????=????????????????????(????>????)的增长速度越来越慢.
不论????的值比????的值大多少,在一定范围内,????????????????????可能会大于????????,但由于????????????????????的增长最终会慢于????????的增长,
因此总会存在一个????????,当????>????????时,恒有?????????????????????
实验探究
例题讲解
例1 下列函数中,随着x的增大,函数值的增长速度最快是( )
????.????=24????????????
?
????.????=????30
?
????.????=????24
?
????.????=24?3????
?
变式1 下列函数中,随着x的增大,函数值的增长越来越慢是( )
????.????=4?3????
?
????.????=4????????????
?
????.????=????6
?
????.????=4????
?
例题讲解
例2 在2h内将某种药物注射进患者的血液中.在注射期间,血液中的药物含量呈线性增加;停止射后,血液中的药物含量呈指数衰减.能反映血液中药物含量Q随时间t变化的图象是( )
例题讲解
例3 高为H,满缸水量为V的鱼缸的轴截面如图所示,其底部破了一个
小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为v,则函数v=f(h)的大致图象是( )
小组讨论
思考 假设有一套住房的房价从2002年的20万元上涨到2012年的40万元.下表给出了两种价格增长方式,其中P1是按直线上升的房价,P2是按指数增长的房价,t是2002年以来经过的年数.
(1)求函数P1=f(t)的解析式;
(2)求函数P2=g(t)的解析式;
(3)完成上表空格中的数据,并在同一直角坐标系中画出两个函数的图象,然后比较两种价格增长方式的差异.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}t
0
5
10
15
20
P1/万元
20
40
P2/万元
20
40
本节课心情指数:
还有哪些困惑:
本节课对数学知识的重大发现:
进一步体悟了探究数学知识的神器(思想与方法):
课堂小结
讲课人:XX
1.理解函数模型是描述客观世界中变量关系和规律的重要工具。
2.在实际情境中,会选择合适的函数类型刻画现实问题的变化规律。
3.比较对数函数、一次函数、指数函数增长速度的差异,理解“对数增长”“直线上升”“指数爆炸”等术语的现实含义。
教学目标
重点
难点
我们学习过的一次函数、二次函数、反比例函数、幂函数、指数函数、对数函数中,哪些函数在定义域上是增函数?
问题导入
问题导入
都是增函数,但是增长方式的差异。
下面就来研究一次函数、指数函数和对数函数增长方式的差异.
探究:观察函数????=????????,????=????????,????=????????????????????,探索它们在区间[0,+∞)上的增长差异,思考以下几个问题.
?
实验探究
问题1:三个函数在区间[????,+∞)上的图象有什么特点?
?
问题2:当x趋于无穷大时,三个函数中哪个函数的增长最快?哪个最慢?
小组讨论
指数函数、一次函数与对数函数增长的差异
{EB344D84-9AFB-497E-A393-DC336BA19D2E}
指数函数
一次函数
对数函数
解析式
y=ax(a>1)
y=kx(k>0)
y=logax(a>1)
单调性
在[0,+∞)上单调递增
图象
(随x的增大)
趋向于和x轴_____
呈直线上升
趋向于和x轴_____
增长速度
(随x的增大)
y的增长速度越来越___
y的增长速度_ _
y的增长速度越来越___
归纳总结
总会存在一个x0,当x>x0时, __________
垂直
平行
快
慢
ax >kx>logax
不变
实验探究
实验探究
一般地,虽然对数函数????=????????????????????(????>????)与一次函数????=????????(????>????)在区间(????,+∞)上都单调递增,但它们的增长速度不同.
随着????的增大,一次函数????=????????(????>????)保持固定的增长速度,而对数函数????=????????????????????(????>????)的增长速度越来越慢.
不论????的值比????的值大多少,在一定范围内,????????????????????可能会大于????????,但由于????????????????????的增长最终会慢于????????的增长,
因此总会存在一个????????,当????>????????时,恒有?????????????????????
实验探究
例题讲解
例1 下列函数中,随着x的增大,函数值的增长速度最快是( )
????.????=24????????????
?
????.????=????30
?
????.????=????24
?
????.????=24?3????
?
变式1 下列函数中,随着x的增大,函数值的增长越来越慢是( )
????.????=4?3????
?
????.????=4????????????
?
????.????=????6
?
????.????=4????
?
例题讲解
例2 在2h内将某种药物注射进患者的血液中.在注射期间,血液中的药物含量呈线性增加;停止射后,血液中的药物含量呈指数衰减.能反映血液中药物含量Q随时间t变化的图象是( )
例题讲解
例3 高为H,满缸水量为V的鱼缸的轴截面如图所示,其底部破了一个
小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为v,则函数v=f(h)的大致图象是( )
小组讨论
思考 假设有一套住房的房价从2002年的20万元上涨到2012年的40万元.下表给出了两种价格增长方式,其中P1是按直线上升的房价,P2是按指数增长的房价,t是2002年以来经过的年数.
(1)求函数P1=f(t)的解析式;
(2)求函数P2=g(t)的解析式;
(3)完成上表空格中的数据,并在同一直角坐标系中画出两个函数的图象,然后比较两种价格增长方式的差异.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}t
0
5
10
15
20
P1/万元
20
40
P2/万元
20
40
本节课心情指数:
还有哪些困惑:
本节课对数学知识的重大发现:
进一步体悟了探究数学知识的神器(思想与方法):
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
