人教版物理九年级全一册 第17章第2节 欧姆定律2课件(共26张PPT)
文档属性
| 名称 | 人教版物理九年级全一册 第17章第2节 欧姆定律2课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 696.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-25 19:57:01 | ||
图片预览





文档简介
(共26张PPT)
欧姆定律
(第一课时 欧姆定律)
一、复习归纳:
电流与电压、电阻的关系。
当电阻R一定时,电流I与电压U成正比。
当电压U一定时,电流I与电阻R成反比。
二、欧姆定律内容:
导体中的电流,跟导体两端的电压成正比,跟导体的电阻成反比。
说明:
①适用条件:纯电阻电路(即用电器工作时,消耗的电能完全转化为内能);
②I、U、R对应同一导体或同一段电路,不同时刻、不同导体或不同段电路三者不能混用,应加角码区别。
③同一导体(即R不变),则I与U成正比; 同一电源(即U不变),则I与R成反比。
揭示了电流与电压、电阻的关系。
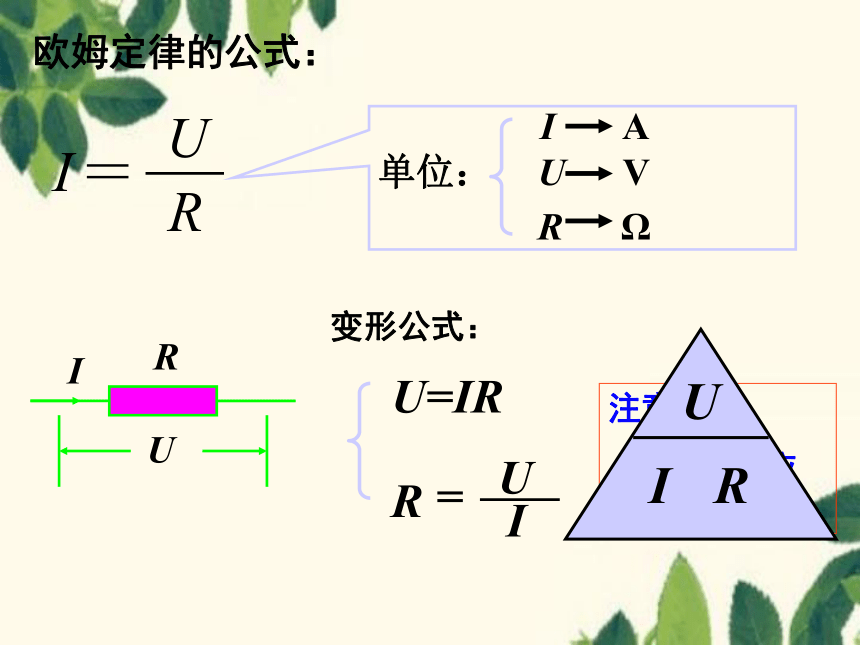
欧姆定律的公式:
I
R
U
=
变形公式:
U=IR
R
=
I
U
R
U
I
注意:
必须对应于同一段电路。
R Ω
单位:
I A
U V
R
U
I
U=IR
R
=
I
U
意义:导体中的电流,跟导体两端的电压成正比,跟导体的电阻成反比。(决定式)
意义:电压在数值上等于导体中的电流跟导体的电阻的乘积。(计算式)
意义:电阻在数值上等于导体两端的电压跟导体中的电流的比值。(计算式)
R
U
I=
各个公式的意义:
车床照明灯的电压是36V,它正常工作时灯丝的电阻是30Ω。求通过灯丝的电流。
R=30Ω
I=?
U=36V
应用1:已知电压、电阻,求电流。
(2)列出已知条件和所求量
解题步骤:
(1)画电路图(简图)
(3)求解I
解:通过灯丝的电流
I=
U
R
36V
30Ω
=
=
1.2A
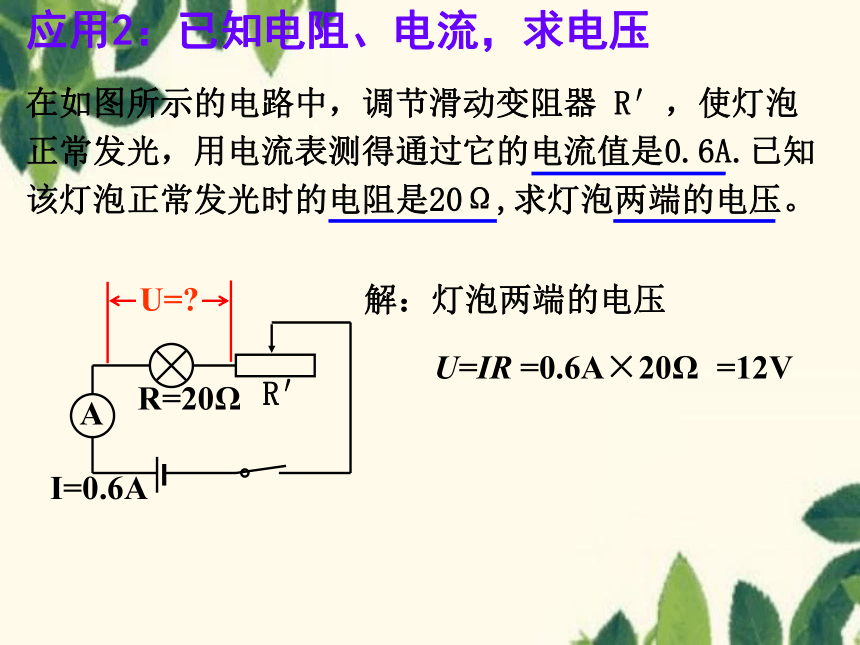
应用2:已知电阻、电流,求电压
在如图所示的电路中,调节滑动变阻器 R′,使灯泡正常发光,用电流表测得通过它的电流值是0.6A.已知该灯泡正常发光时的电阻是20Ω,求灯泡两端的电压。
解:灯泡两端的电压
U=IR
=0.6A×20Ω
=12V
R=20Ω
A
R′
I=0.6A
U=
U=220V
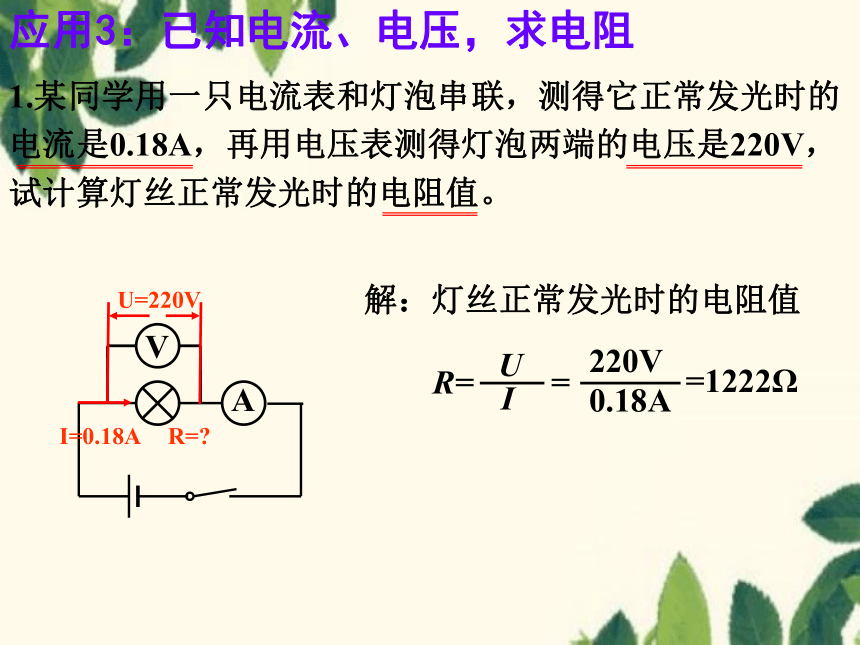
1.某同学用一只电流表和灯泡串联,测得它正常发光时的电流是0.18A,再用电压表测得灯泡两端的电压是220V,试计算灯丝正常发光时的电阻值。
应用3:已知电流、电压,求电阻
V
A
R=
U
I
220V
0.18A
=
=1222Ω
解:灯丝正常发光时的电阻值
I=0.18A
R=
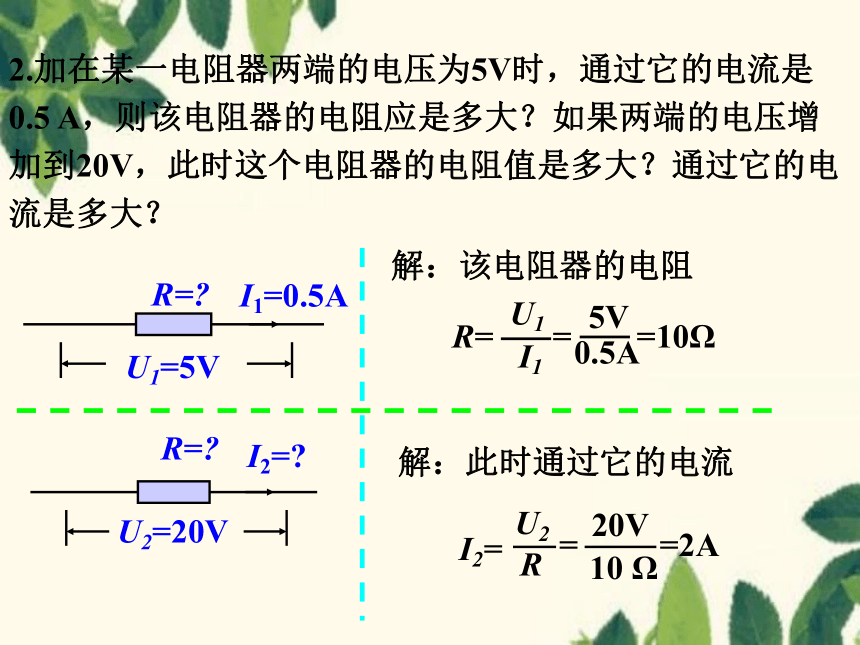
2.加在某一电阻器两端的电压为5V时,通过它的电流是0.5 A,则该电阻器的电阻应是多大?如果两端的电压增加到20V,此时这个电阻器的电阻值是多大?通过它的电流是多大?
U2=20V
R=
I2=
I1=0.5A
R=
U1=5V
解:该电阻器的电阻
U1
I1
5V
0.5A
R=
=10Ω
=
解:此时通过它的电流
R
U2
10 Ω
20V
=
I2=
=2A
例1:试电笔内的大电阻的阻值为880 kΩ,氖管和人体的电阻都比这个值小得多,可以不计。问使用时流过人体的电流是多少?
解:使用时流过人体的电流
I=
U
R
220V
880×103Ω
=
=0.25×10-3 A=0.25mA
例2:实验中测得一个未知电阻两端的电压为2.4V,流过的电流为160mA,这个电阻的阻值是多少?
例3:已知一个电阻的阻值是24Ω,流过它的电流是150mA,则这个电阻两端的电压是多少?
I
解:这个电阻的阻值:
R= = = 15Ω
U
2.4V
0.16A
解:这个电阻两端的电压
U=IR=0.15A×24 Ω=3.6V
1、某灯泡的正常工作的电压是24V,电路中通过的电流是0.5A,若把它接入36V的电源上,为了能使灯泡正常工作,需要串联一个多大的电阻?
牛刀小试:
答案:串联的电阻R=24Ω
2、如图所示,R1=20Ω ,开关S闭合后电流表A的示数为2.7A,电流表A1的示数为1.8A。求:(1)电源的电压;(2)电阻R2的阻值.
答案:电源电压U=36V 电阻R2 的阻值R2 = 40Ω
二 欧姆定律及其应用
(第二课时 电阻的串联和并联)
电阻的串联与并联
R1
R2
R1
R2
R串
R并
电阻串联相当于增大导体的长度。
串联总电阻比任何一个分电阻都大。
电阻并联相当于增大导体的横截面积。
并联总电阻比任何一个分电阻都小。
等效替代法
1、串联电路的总电阻与分电阻的关系
R1
R2
U1
U总
U2
由欧姆定律变形公式可得:
U1=IR1 U2=IR2 U总=IR总 串联电路中:U总=U1+U2
即:IR总=IR1+IR2 R总=R1+R2
结论:串联电路的总电阻比任何一个分电阻都大。
电阻的串联(理论推导)
I
I
I
R总
I
U总
R1
R2
U
I1
I总
I2
由欧姆定律可得:
并联电路中:I总=I1+I2
即
结论:并联电路的总电阻比任何一个分电阻都小。
电阻的并联(理论推导)
2、并联电路的总电阻与分电阻的关系
I总
R总
U
R1
U
I1=
R2
U
I2=
R总
U
I总=
R总
U
R1
U
=
R2
U
+
R总
1
R1
1
=
R2
1
+
1、串联电路的总电阻等于各串联电阻之和。
R串= R1+ R2
2、并联电路的总电阻的倒数等于各并联电阻倒数之和。
n个阻值相同的电阻R0串联,总电阻
n个阻值相同的电阻 R0并联,总电阻
R串=nR0
R并
R1
R2
1
1
1
=
+
R1R2
R并=
R1+R2
R0
R并=
n
当堂训练
1.将4Ω和12Ω的电阻串联接入电路总电阻为 。
2.将两个电阻均为6Ω的电阻串联接入电路总电阻为 。
3.将5个20Ω的电阻串联,总电阻为 Ω,若将n个阻值为R的电阻串联,总电阻为 。
4.将两个电阻串联,总电阻为72 Ω,若一个电阻为30 Ω,另一个是 。
5.已知R1=20Ω,R2=60Ω,则R1与R2并联后的总电阻R= .
6.若将n个阻值为R的电阻并联,总电阻为 。
16Ω
12Ω
100
nR
42Ω
15Ω
R
n
n
串联电路 并联电路
电
路
图
电流 I = I1 =I2 I =I1+I2
电压 U =U1+U2 U =U1=U2
电
阻 R =R1+R2
R = nR0
电压、电流分配关系
R并
R1
R2
1
1
1
=
+
R =
n
R0
I2
R1
I1
R2
=
U2
R2
U1
R1
=
R并 =
R1+R2
R1R2
I1
I2
I
I1
I2
I
R1
R1
R2
R2
例:在如图的电路中,R1=20 , R2=60 ,
电源电压U=36V,请用两种方法求干路的总电流I和两灯总电阻R。
R1
U=36V
R2
I
I2
I1
解法一:在并联电路中: U1=U2=U=36V
则
干路的总电流:I=I1+I2=1.8A+0.6A=2.4A
两灯总电阻:R= = =15
U
I
36V
2.4A
I2= = =0.6A
U2
R2
36V
60
I1= = =1.8A
U1
R1
36V
20
解法二:
干路的总电流:I= = =2.4A
U
R
36V
15
在并联电路中:
R= = =15
R1+R2
R1R2
20 × 60
20 + 60
1、电源电压保持不变, R1 = R2 = R3 = 20Ω ,当S1、S2都断开,电流表示数是0.3A,求:(1)电源电压;(2)S1、S2都闭合时,电流表示数是多少?
A
R1
R2
R3
S1
S2
解:(1)当S1、S2都断开时, R1
与R2串联在电路中,R3断路。
电源电压:
U=I(R1+R2)=0.3A×(20Ω+20Ω)
=12V
(2)当S1、S2都闭合时,R1与R3并联,R2被短路。此时电路中总电阻
R1+R3
R1R3
20Ω× 20Ω
20Ω+ 20Ω
R总= = = 10Ω
电流表示数
I ′= = = 1.2A
U
R总
12V
10Ω
2、如图,电源电压为6V不变,灯L1的电阻为12Ω,灯L2的电阻为9Ω,灯L3的电阻为18Ω.求:
(1)开关S1、S2同时断开和闭合时,电压表、电流表的示数分别为多少?
(2)开关S1、S2同时断开和闭合时,电流之比是多少?
A
V
L1
L2
L3
S1
S2
2.如图,电源电压为6V不变,灯L1的电阻为12Ω ,灯L2的电阻为9Ω , 灯L3的电阻为18Ω 。
求:1)开关S1、S2同时断开和闭合时,电压表、电流表的示数分别为多少?
S1、S2同时断开时:
L1
V
A
L 1
L 3
V
L1L3串联,电压表测 L 1两端电压
A
L2
S1
S2
L3
S1、S2同时闭合时:
L2L3并联,L1
和电压表被短路.
A
V
L1
L2
L3
S1
S2
2.如图,电源电压为6V不变,灯L1的电阻为12Ω ,灯L2的电阻为9Ω ,灯L3的电阻为18Ω 。
求:1)开关S1、S2同时断开和闭合时,电压表的示数分别为多少?
解:当S1、S2都断开时,L2断路,L1、L3
串联,即I1 = I2 = I3
U 6V 6V
I= = = =0.2A
R1+R3 12 Ω +18 Ω 30 Ω
U1=I1R1=0.2A× 12 Ω =2.4 V
当S1、S2都闭合时,L1被短路 U1=0V
A
V
L1
L2
L3
S1
S2
2.如图,电源电压为6V不变,灯L1的电阻为12Ω ,灯L2的电阻
为9Ω , 灯L3的电阻为18Ω .
求:2)开关S1、S2同时断开和闭合时,电流之比是多少?
A
V
L1
L2
L3
S1
S2
解:当S1、S2都断开时,L2断路,L1、L3
串联,即I1 = I2 = I3
U 6V 6V
I= = = =0.2A
R1+R3 12 Ω +18 Ω 30 Ω
当S1、S2都闭合时,L1被短路,L2、L3
并联,U = U2 = U3
R2 R3 9 Ω × 18 Ω
R = = = 6 Ω
R2+ R3 9 Ω + 18 Ω
U 6V
I = = = 1A
R 6 Ω
即,电流比是: I断 0.2A 1
= =
I合 1A 5
人物简介
乔治·西蒙·欧姆 (Georg Simon Ohm,1787—1845)一个天才的研究者,1787年5月16日生于德国埃尔兰根城,父亲自学了数学和物理方面的知识,并教给少年时期的欧姆,唤起了欧姆对科学的兴趣。然而他的成就对我们后人的意义是非常远大的。
欧姆是德国物理学家,提出了经典电磁理论中著名的欧姆定律。为纪念其重要贡献, 人们将其名字作为电阻的单位。欧姆的名字也被用于其他物理及相关技术内容中,比如“欧姆接触”、“欧姆杀菌”,“欧姆表”等。
乔治·西蒙·欧姆研究成果
欧姆定律
(第一课时 欧姆定律)
一、复习归纳:
电流与电压、电阻的关系。
当电阻R一定时,电流I与电压U成正比。
当电压U一定时,电流I与电阻R成反比。
二、欧姆定律内容:
导体中的电流,跟导体两端的电压成正比,跟导体的电阻成反比。
说明:
①适用条件:纯电阻电路(即用电器工作时,消耗的电能完全转化为内能);
②I、U、R对应同一导体或同一段电路,不同时刻、不同导体或不同段电路三者不能混用,应加角码区别。
③同一导体(即R不变),则I与U成正比; 同一电源(即U不变),则I与R成反比。
揭示了电流与电压、电阻的关系。
欧姆定律的公式:
I
R
U
=
变形公式:
U=IR
R
=
I
U
R
U
I
注意:
必须对应于同一段电路。
R Ω
单位:
I A
U V
R
U
I
U=IR
R
=
I
U
意义:导体中的电流,跟导体两端的电压成正比,跟导体的电阻成反比。(决定式)
意义:电压在数值上等于导体中的电流跟导体的电阻的乘积。(计算式)
意义:电阻在数值上等于导体两端的电压跟导体中的电流的比值。(计算式)
R
U
I=
各个公式的意义:
车床照明灯的电压是36V,它正常工作时灯丝的电阻是30Ω。求通过灯丝的电流。
R=30Ω
I=?
U=36V
应用1:已知电压、电阻,求电流。
(2)列出已知条件和所求量
解题步骤:
(1)画电路图(简图)
(3)求解I
解:通过灯丝的电流
I=
U
R
36V
30Ω
=
=
1.2A
应用2:已知电阻、电流,求电压
在如图所示的电路中,调节滑动变阻器 R′,使灯泡正常发光,用电流表测得通过它的电流值是0.6A.已知该灯泡正常发光时的电阻是20Ω,求灯泡两端的电压。
解:灯泡两端的电压
U=IR
=0.6A×20Ω
=12V
R=20Ω
A
R′
I=0.6A
U=
U=220V
1.某同学用一只电流表和灯泡串联,测得它正常发光时的电流是0.18A,再用电压表测得灯泡两端的电压是220V,试计算灯丝正常发光时的电阻值。
应用3:已知电流、电压,求电阻
V
A
R=
U
I
220V
0.18A
=
=1222Ω
解:灯丝正常发光时的电阻值
I=0.18A
R=
2.加在某一电阻器两端的电压为5V时,通过它的电流是0.5 A,则该电阻器的电阻应是多大?如果两端的电压增加到20V,此时这个电阻器的电阻值是多大?通过它的电流是多大?
U2=20V
R=
I2=
I1=0.5A
R=
U1=5V
解:该电阻器的电阻
U1
I1
5V
0.5A
R=
=10Ω
=
解:此时通过它的电流
R
U2
10 Ω
20V
=
I2=
=2A
例1:试电笔内的大电阻的阻值为880 kΩ,氖管和人体的电阻都比这个值小得多,可以不计。问使用时流过人体的电流是多少?
解:使用时流过人体的电流
I=
U
R
220V
880×103Ω
=
=0.25×10-3 A=0.25mA
例2:实验中测得一个未知电阻两端的电压为2.4V,流过的电流为160mA,这个电阻的阻值是多少?
例3:已知一个电阻的阻值是24Ω,流过它的电流是150mA,则这个电阻两端的电压是多少?
I
解:这个电阻的阻值:
R= = = 15Ω
U
2.4V
0.16A
解:这个电阻两端的电压
U=IR=0.15A×24 Ω=3.6V
1、某灯泡的正常工作的电压是24V,电路中通过的电流是0.5A,若把它接入36V的电源上,为了能使灯泡正常工作,需要串联一个多大的电阻?
牛刀小试:
答案:串联的电阻R=24Ω
2、如图所示,R1=20Ω ,开关S闭合后电流表A的示数为2.7A,电流表A1的示数为1.8A。求:(1)电源的电压;(2)电阻R2的阻值.
答案:电源电压U=36V 电阻R2 的阻值R2 = 40Ω
二 欧姆定律及其应用
(第二课时 电阻的串联和并联)
电阻的串联与并联
R1
R2
R1
R2
R串
R并
电阻串联相当于增大导体的长度。
串联总电阻比任何一个分电阻都大。
电阻并联相当于增大导体的横截面积。
并联总电阻比任何一个分电阻都小。
等效替代法
1、串联电路的总电阻与分电阻的关系
R1
R2
U1
U总
U2
由欧姆定律变形公式可得:
U1=IR1 U2=IR2 U总=IR总 串联电路中:U总=U1+U2
即:IR总=IR1+IR2 R总=R1+R2
结论:串联电路的总电阻比任何一个分电阻都大。
电阻的串联(理论推导)
I
I
I
R总
I
U总
R1
R2
U
I1
I总
I2
由欧姆定律可得:
并联电路中:I总=I1+I2
即
结论:并联电路的总电阻比任何一个分电阻都小。
电阻的并联(理论推导)
2、并联电路的总电阻与分电阻的关系
I总
R总
U
R1
U
I1=
R2
U
I2=
R总
U
I总=
R总
U
R1
U
=
R2
U
+
R总
1
R1
1
=
R2
1
+
1、串联电路的总电阻等于各串联电阻之和。
R串= R1+ R2
2、并联电路的总电阻的倒数等于各并联电阻倒数之和。
n个阻值相同的电阻R0串联,总电阻
n个阻值相同的电阻 R0并联,总电阻
R串=nR0
R并
R1
R2
1
1
1
=
+
R1R2
R并=
R1+R2
R0
R并=
n
当堂训练
1.将4Ω和12Ω的电阻串联接入电路总电阻为 。
2.将两个电阻均为6Ω的电阻串联接入电路总电阻为 。
3.将5个20Ω的电阻串联,总电阻为 Ω,若将n个阻值为R的电阻串联,总电阻为 。
4.将两个电阻串联,总电阻为72 Ω,若一个电阻为30 Ω,另一个是 。
5.已知R1=20Ω,R2=60Ω,则R1与R2并联后的总电阻R= .
6.若将n个阻值为R的电阻并联,总电阻为 。
16Ω
12Ω
100
nR
42Ω
15Ω
R
n
n
串联电路 并联电路
电
路
图
电流 I = I1 =I2 I =I1+I2
电压 U =U1+U2 U =U1=U2
电
阻 R =R1+R2
R = nR0
电压、电流分配关系
R并
R1
R2
1
1
1
=
+
R =
n
R0
I2
R1
I1
R2
=
U2
R2
U1
R1
=
R并 =
R1+R2
R1R2
I1
I2
I
I1
I2
I
R1
R1
R2
R2
例:在如图的电路中,R1=20 , R2=60 ,
电源电压U=36V,请用两种方法求干路的总电流I和两灯总电阻R。
R1
U=36V
R2
I
I2
I1
解法一:在并联电路中: U1=U2=U=36V
则
干路的总电流:I=I1+I2=1.8A+0.6A=2.4A
两灯总电阻:R= = =15
U
I
36V
2.4A
I2= = =0.6A
U2
R2
36V
60
I1= = =1.8A
U1
R1
36V
20
解法二:
干路的总电流:I= = =2.4A
U
R
36V
15
在并联电路中:
R= = =15
R1+R2
R1R2
20 × 60
20 + 60
1、电源电压保持不变, R1 = R2 = R3 = 20Ω ,当S1、S2都断开,电流表示数是0.3A,求:(1)电源电压;(2)S1、S2都闭合时,电流表示数是多少?
A
R1
R2
R3
S1
S2
解:(1)当S1、S2都断开时, R1
与R2串联在电路中,R3断路。
电源电压:
U=I(R1+R2)=0.3A×(20Ω+20Ω)
=12V
(2)当S1、S2都闭合时,R1与R3并联,R2被短路。此时电路中总电阻
R1+R3
R1R3
20Ω× 20Ω
20Ω+ 20Ω
R总= = = 10Ω
电流表示数
I ′= = = 1.2A
U
R总
12V
10Ω
2、如图,电源电压为6V不变,灯L1的电阻为12Ω,灯L2的电阻为9Ω,灯L3的电阻为18Ω.求:
(1)开关S1、S2同时断开和闭合时,电压表、电流表的示数分别为多少?
(2)开关S1、S2同时断开和闭合时,电流之比是多少?
A
V
L1
L2
L3
S1
S2
2.如图,电源电压为6V不变,灯L1的电阻为12Ω ,灯L2的电阻为9Ω , 灯L3的电阻为18Ω 。
求:1)开关S1、S2同时断开和闭合时,电压表、电流表的示数分别为多少?
S1、S2同时断开时:
L1
V
A
L 1
L 3
V
L1L3串联,电压表测 L 1两端电压
A
L2
S1
S2
L3
S1、S2同时闭合时:
L2L3并联,L1
和电压表被短路.
A
V
L1
L2
L3
S1
S2
2.如图,电源电压为6V不变,灯L1的电阻为12Ω ,灯L2的电阻为9Ω ,灯L3的电阻为18Ω 。
求:1)开关S1、S2同时断开和闭合时,电压表的示数分别为多少?
解:当S1、S2都断开时,L2断路,L1、L3
串联,即I1 = I2 = I3
U 6V 6V
I= = = =0.2A
R1+R3 12 Ω +18 Ω 30 Ω
U1=I1R1=0.2A× 12 Ω =2.4 V
当S1、S2都闭合时,L1被短路 U1=0V
A
V
L1
L2
L3
S1
S2
2.如图,电源电压为6V不变,灯L1的电阻为12Ω ,灯L2的电阻
为9Ω , 灯L3的电阻为18Ω .
求:2)开关S1、S2同时断开和闭合时,电流之比是多少?
A
V
L1
L2
L3
S1
S2
解:当S1、S2都断开时,L2断路,L1、L3
串联,即I1 = I2 = I3
U 6V 6V
I= = = =0.2A
R1+R3 12 Ω +18 Ω 30 Ω
当S1、S2都闭合时,L1被短路,L2、L3
并联,U = U2 = U3
R2 R3 9 Ω × 18 Ω
R = = = 6 Ω
R2+ R3 9 Ω + 18 Ω
U 6V
I = = = 1A
R 6 Ω
即,电流比是: I断 0.2A 1
= =
I合 1A 5
人物简介
乔治·西蒙·欧姆 (Georg Simon Ohm,1787—1845)一个天才的研究者,1787年5月16日生于德国埃尔兰根城,父亲自学了数学和物理方面的知识,并教给少年时期的欧姆,唤起了欧姆对科学的兴趣。然而他的成就对我们后人的意义是非常远大的。
欧姆是德国物理学家,提出了经典电磁理论中著名的欧姆定律。为纪念其重要贡献, 人们将其名字作为电阻的单位。欧姆的名字也被用于其他物理及相关技术内容中,比如“欧姆接触”、“欧姆杀菌”,“欧姆表”等。
乔治·西蒙·欧姆研究成果
同课章节目录
- 第十三章 内能
- 第1节 分子热运动
- 第2节 内能
- 第3节 比热容
- 第十四章 内能的利用
- 第1节 热机
- 第2节 热机的效率
- 第3节 能量的转化和守恒
- 第十五章 电流和电路
- 第1节 两种电荷
- 第2节 电流和电路
- 第3节 串联和并联
- 第4节 电流的测量
- 第5节 串、并联电路中电流的规律
- 第十六章 电压 电阻
- 第1节 电压
- 第2节 串、并联电路电压的规律
- 第3节 电阻
- 第4节 变阻器
- 第十七章 欧姆定律
- 第1节 电流与电压和电阻的关系
- 第2节 欧姆定律
- 第3节 电阻的测量
- 第4节 欧姆定律在串、并联电路中的应用
- 第十八章 电功率
- 第1节 电能 电功
- 第2节 电功率
- 第3节 测量小灯泡的电功率
- 第4节 焦耳定律
- 第十九章 生活用电
- 第1节 家庭电路
- 第2节 家庭电路电流过大的原因
- 第3节 安全用电
- 第二十章 电与磁
- 第1节 磁现象 磁场
- 第2节 电生磁
- 第3节 电磁铁 电磁继电器
- 第4节 电动机
- 第5节 磁生电
- 第二十一章 信息的传递
- 第1节 现代顺风耳──电话
- 第2节 电磁波的海洋
- 第3节 广播、电视和移动通信
- 第4节 越来越宽的信息之路
- 第二十二章 能源与可持续发展
- 第1节 能源
- 第2节 核能
- 第3节 太阳能
- 第4节 能源与可持续发展
