人教版新教材必修一4.5 牛顿运动定律的应用 等时圆专题(含答案)
文档属性
| 名称 | 人教版新教材必修一4.5 牛顿运动定律的应用 等时圆专题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 752.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-25 00:00:00 | ||
图片预览


文档简介
人教版新教材必修一等时圆专题(含答案)
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共60.0分)
三个光滑斜轨道、、,它们的倾角依次是、、,这些轨道交于点,现有位于同一竖直线上的三个物体甲、乙、丙分别沿这三个轨道同时从静止自由下滑,如图所示,物体滑到点的先后顺序是( )
A. 甲最先,乙稍后,丙最后 B. 甲、乙、丙同时到达
C. 乙最先,然后甲和丙同时到达 D. 乙最先,甲稍后,丙最后
如图所示,圆柱形的仓库内有三块长度不同的滑板、、,其下端都固定于底部的圆心点,而上端则搁在仓库侧壁,三块滑块与水平面的夹角依次是、、若有三个小孩同时从、、处开始下滑忽略阻力,则( )
A. 处小孩先到点 B. 处小孩先到点
C. 处小孩先到点 D. 、、处小孩同时到点
如图所示,在斜面上有四条光滑细杆,其中杆竖直放置,杆与杆等长,杆与斜面垂直放置,每根杆上都套着一个小滑环图中未画出,四个环分别从点由静止释放,沿、、、滑到斜面上所用的时间依次为、、、,下列关系错误的是
A. B. C. D.
如图所示,一只可视为质点的蚂蚁在半球形碗内缓慢从底部经过点爬到最高点点,之后开始沿碗下滑并再次经过点滑到底部,蚂蚁与碗内各处的动摩擦因数均相同且小于,若最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
A. 点与球心的连线与竖直方向的夹角小于
B. 上爬过程中,蚂蚁所受摩擦力逐渐减小
C. 上爬过程中,蚂蚁所受碗的作用力逐渐增大
D. 上爬过程和下滑过程中,蚂蚁经过点时所受支持力相同
如图所示,、和是竖直平面内三根固定的光滑细杆,、、、、位于同一圆周上,为圆周的最高点,为最低点,为圆心。每根杆上都套着一个小滑环未画出,两个滑环从点无初速释放,一个滑环从点无初速释放,用、、分别表示滑环沿、、到达、所用的时间,则下列关系不正确的是( )
A. B. C. D.
如图为竖直面内的一个圆,从圆上最高点到圆上、两个斜面和,斜面与竖直方向夹角为和,物块从点由静止释放,沿经时间到,沿经时间到则( )
A. 若不计摩擦,则
B. 若不计摩擦,则
C. 若有摩擦且动摩擦因数相同,则
D. 若有摩擦且动摩擦因数相同,则
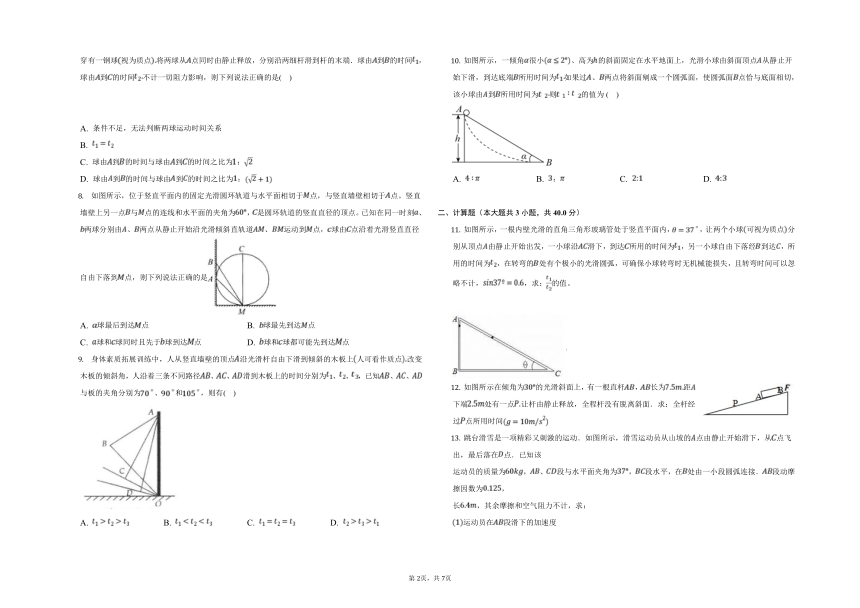
如图所示,倾角为的斜面上有、两点,在点竖直地固定一光滑直杆,点与斜面底端点间置有一光滑的直杆两杆上各穿有一钢球视为质点将两球从点同时由静止释放,分别沿两细杆滑到杆的末端.球由到的时间,球由到的时间不计一切阻力影响,则下列说法正确的是( )
A. 条件不足,无法判断两球运动时间关系
B.
C. 球由到的时间与球由到的时间之比为:
D. 球由到的时间与球由到的时间之比为:
如图所示,位于竖直平面内的固定光滑圆环轨道与水平面相切于点,与竖直墙壁相切于点。竖直墙壁上另一点与点的连线和水平面的夹角为,是圆环轨道的竖直直径的顶点。已知在同一时刻、两球分别由、两点从静止开始沿光滑倾斜直轨道、运动到点,球由点沿着光滑竖直直径自由下落到点,则下列说法正确的是
A. 球最后到达点 B. 球最先到达点
C. 球和球同时且先于球到达点 D. 球和球都可能先到达点
身体素质拓展训练中,人从竖直墙壁的顶点沿光滑杆自由下滑到倾斜的木板上人可看作质点改变木板的倾斜角,人沿着三条不同路径、、滑到木板上的时间分别为、、,已知、、与板的夹角分别为、和,则有( )
A. B. C. D.
如图所示,一倾角很小、高为的斜面固定在水平地面上,光滑小球由斜面顶点从静止开始下滑,到达底端所用时间为如果过、两点将斜面剜成一个圆弧面,使圆弧面点恰与底面相切,该小球由到所用时间为 则 的值为( )
A. B. : C. D.
二、计算题(本大题共3小题,共40.0分)
如图所示,一根内壁光滑的直角三角形玻璃管处于竖直平面内,,让两个小球可视为质点分别从顶点由静止开始出发,一小球沿滑下,到达所用的时间为,另一小球自由下落经到达,所用的时间为,在转弯的处有个极小的光滑圆弧,可确保小球转弯时无机械能损失,且转弯时间可以忽略不计,,求:的值。
如图所示在倾角为的光滑斜面上,有一根直杆,长为距下端处有一点让杆由静止释放,全程杆没有脱离斜面.求:全杆经过点所用时间
跳台滑雪是一项精彩又刺激的运动.如图所示,滑雪运动员从山坡的点由静止开始滑下,从点飞出,最后落在点.已知该
运动员的质量为,、段与水平面夹角为,段水平,在处由一小段圆弧连接.段动摩擦因数为,
长,其余摩擦和空气阻力不计,求:
运动员在段滑下的加速度
运动员在空中飞行的时间
运动员落到点时的速度.
答案和解析
1.【答案】
【解析】
【分析】本题考查了匀变速直线运动的位移与时间的关系、从受力确定运动情况、用牛顿运动定律分析斜面体模型的相关知识,试题难度较易
【解答】设三个光滑斜轨道的共同底边长为,当物体沿着与水平方向成角的斜轨道下滑时,加速度,斜轨道长,物体沿光滑斜轨道下滑的时间由可得当时,,,此时值最小,因此乙最先到达点;当和时,,因此甲和丙滑行的时间相同,在乙之后同时到达点,故C正确.
2.【答案】
【解析】
【分析】
根据牛顿第二定律和匀变速直线运动规律,分别计算出小孩从、、三块滑板到所用的时间进行比较即可。
解决本题的关键是根据牛顿第二定律对物体进行受力分析,并根据匀变速直线运动规律计算出时间。
【解答】
斜面上小孩的加速度:
斜面的长度,
得:,
,
把与水平面的夹角分别代入得:,
,,
知,
即先到,同时到,故B正确,ACD错误。
故选B。
3.【答案】
【解析】
【分析】
根据等时圆模型,可知从圆上最高点沿任意一条弦滑到底所用时间相同,故沿和滑到底的时间相同,不是一条完整的弦,时间最短,长度超过一条弦,时间最长.
如果不假思考,套用结论,就会落入等时圆”的陷阱,要注意点不是最高点,难度适中
【解答】
以为直径画园,根据等时圆模型,对小滑环,受重力和支持力,将重力沿杆的方向和垂直杆的方向正交分解,根据牛顿第二定律得小滑环做初速为零的匀加速直线运动的加速度为为杆与竖直方向的夹角
由图中的直角三角形可知,小滑环的位移
所以,与无关,
可知从圆上最高点沿任意一条弦滑到底所用时间相同,故沿和滑到底的时间相同,即,不是一条完整的弦,时间最短,即,长度超过一条弦,时间最长,即故ABC正确,不正确
因选不正确的,故选:.
4.【答案】
【解析】解:蚂蚁缓慢上爬,可以认为蚂蚁处于平衡状态,则合力始终为零,受力分析,根据共点力平衡有:
,
A、在点恰好滑动,则:
由于小于,所以点与球心的连线与竖直方向的夹角小于故A正确;
B、因为点的与球心的连线与竖直方向的夹角比点的小,所以在点碗对蚂蚁的摩擦力小于在点的摩擦力,在上爬过程中,蚂蚁所受摩擦力逐渐增大,故B错误;
C、在蚂蚁向上爬的过程中,碗对蚂蚁的作用力都等于蚂蚁的重力,所以在上爬过程中,蚂蚁所受碗的作用力不变,故C错误。
D、蚂蚁沿碗下滑的过程中做圆周运动,需要一定的向心力,所以下滑的过程中蚂蚁受到的支持力大。故D错误
故选:。
蚂蚁缓慢上爬,可以认为蚂蚁处于平衡状态,合力为零,蚂蚁所受的摩擦力为静摩擦力,与重力延斜面向下的分力平衡,所以越往上爬,所受静摩擦力越大。
解决本题的关键能够正确地受力分析,运用共点力平衡进行求解。
5.【答案】
【解析】
【分析】
本题关键从众多的杆中抽象出一根杆,假设其与水平方向的夹角为,然后根据牛顿第二定律求出加速度,再根据运动学公式求出时间表达式讨论。
先受力分析后根据牛顿第二定律计算出滑环沿任意一根杆滑动的加速度,然后根据位移时间关系公式计算出时间,对表达式分析,得出时间与各因素的关系后得出结论。
【解答】
解:设与竖直方向的夹角为,由几何关系得与竖直方向的夹角为,环沿下滑时的加速度大小为,
沿下滑时的加速度大小为,
设长为,由几何关系得长为,
根据运动学公式有,,,
得,,
由此得到;由于,同理可得到,因此,,故A错误,符合题意,BCD正确,不符合题意。
故选:。
6.【答案】
【解析】解:设圆的直径为.
A、不计摩擦,取任一路线研究,设斜面与竖直方向的夹角为,则加速度为,位移为
由得,与无关,则得:故AB错误.
C、若有摩擦,设动摩擦因数为,则根据牛顿第二定律得:
由得,则越大,越大,故有故C正确,D错误.
故选:
明确几何关系,根据牛顿第二定律得到加速度,由位移公式表示出运动时间,即可进行比较.
本题关键从众多的杆中抽象出一根杆,假设其与水平方向的夹角为,然后根据牛顿第二定律求出加速度,再根据运动学公式求出时间表达式进行讨论.
7.【答案】
【解析】解:质点沿杆下滑的加速度,位移,由可得:;
质点沿杆下滑,令,则位移,加速度为:
根据位移时间关系有
可得运动时间为:
所以可得::
故选:
根据牛顿第二定律求出加速度的大小,结合位移时间公式求出运动的时间,再进行比较.
解决本题的关键正确地受力分析,运用牛顿第二定律结合运动学公式进行求解,知道加速度是联系力学和运动学的桥梁.
8.【答案】
【解析】
【分析】
根据几何关系分别求出各个轨道的位移,根据牛顿第二定律求出加速度,再根据匀变速直线运动的位移时间公式求出运动的时间,从而比较出到达点的先后顺序。
解决本题的关键根据牛顿第二定律求出各段的加速度,运用匀变速直线运动的位移时间公式进行求解。
【解答】
对于段,位移,加速度,根据得,;
对于段,位移,加速度,由得,;
对于段,位移,加速度,由得,。知最小,故C正确,、、D错误。
故选C。
9.【答案】
【解析】
【分析】
将看做圆的直径,由几何关系判断、、三点与圆周的位置关系,由等时圆的特点解决。
本题主要考查等时圆问题,知道在竖直平面内的圆中,从最高点沿光滑杆滑到圆周上各点用时相等是解题的关键,难度不大。
【解答】
在竖直平面内的圆中,从最高点沿光滑杆滑到圆周上各点用时相等。由题意可知,由于、、与板的夹角分别为、和,故由数学知识可知点在以为直径的圆上,而点在圆外、点在圆内,故可知人沿着三条不同路径、、滑到木板上的时间关系为:,故A正确,BCD错误。
故选A。
10.【答案】
【解析】
【分析】
本题主要考查了物理建模的能力,考查了牛顿第二定律的应用和单摆模型。
要求两种运动时间的比值需要求出两种运动的时间,光滑小球从斜劈顶点由静止开始下滑,做匀加速直线运动,这是一个同学的熟悉的运动模型,应用牛顿运动定律和运动学公式即可求解,但是把斜面剜成圆弧面则不易求解,同学会感觉无从下手,无限分割,变曲为直,数学知识又跟不上,几乎无法求解.但是分析发现剜成圆弧面在点与底面相切,以点为中心,在其右侧补偿一个对称的圆弧面,小球的运动即变成了一个同学们都熟悉的简谐运动模型了,小球沿弧运动的时间为类单摆运动周期的四分之一。
【解答】:
第一种情况,小球做匀加速运动,,第二种情况,小球做简谐运动,时间 ,为圆弧槽的半径,,所以,故A正确,BCD错误。
故选A。
11.【答案】解:设三边分别为、、
第一个小球由滑下时加速度为
由位移时间公式得
解得
第二个小球沿段有
解得
该球到达点的速度大小为
沿水平段运动时有,得
则
故
答:的值为。
【解析】根据牛顿第二定律求出小球沿下滑的加速度,由位移公式求出时间与长度的关系。另一小球在段做自由落体运动,段做匀速直线运动,分别求出两段时间与位移大小的关系,再求解的值。
本题要学会用相同的量表示、,分段运用牛顿第二定律和运动学公式相结合求出时间的表达式,也可以通过作速度时间图象进行分析。
12.【答案】解:对杆受力分析,根据牛顿第二定律可知:,
解得:
到达点时有:,
解得:
点到达点时有:,
解得:
全杆经过点所用时间为:
答:全杆经过点所用时间为
【解析】杆全部通过点需时间为杆的上端到达点的时间减去杆的下端到达点的时间,根据匀加速直线运动的位移时间公式即可求解.
本题考查分析处理匀加速直线运动运动的能力.关键抓住杆全部通过点时间如何理解.
13.【答案】解:段:匀加速直线运动,根据牛顿第二定律可知:
解得:
段:根据速度位移公式有:,
解得:
段:平抛运动为:
在水平方向上有:
在竖直方向上有:
联立解得:
在段做平抛运动,则有:
故D点速度为:
答:运动员在段滑下的加速度为
运动员在空中飞行的时间为
运动员落到点时的速度为
【解析】根据牛顿第二定律求得下滑的加速度;
从点做平抛运动,根据平抛运动的特点求得运动时间和速度
本题考查了求运动员的落点位置,分析清楚运动员的运动过程,应用平抛运动规律即可正确解题,解题时注意数学知识的应用.
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共60.0分)
三个光滑斜轨道、、,它们的倾角依次是、、,这些轨道交于点,现有位于同一竖直线上的三个物体甲、乙、丙分别沿这三个轨道同时从静止自由下滑,如图所示,物体滑到点的先后顺序是( )
A. 甲最先,乙稍后,丙最后 B. 甲、乙、丙同时到达
C. 乙最先,然后甲和丙同时到达 D. 乙最先,甲稍后,丙最后
如图所示,圆柱形的仓库内有三块长度不同的滑板、、,其下端都固定于底部的圆心点,而上端则搁在仓库侧壁,三块滑块与水平面的夹角依次是、、若有三个小孩同时从、、处开始下滑忽略阻力,则( )
A. 处小孩先到点 B. 处小孩先到点
C. 处小孩先到点 D. 、、处小孩同时到点
如图所示,在斜面上有四条光滑细杆,其中杆竖直放置,杆与杆等长,杆与斜面垂直放置,每根杆上都套着一个小滑环图中未画出,四个环分别从点由静止释放,沿、、、滑到斜面上所用的时间依次为、、、,下列关系错误的是
A. B. C. D.
如图所示,一只可视为质点的蚂蚁在半球形碗内缓慢从底部经过点爬到最高点点,之后开始沿碗下滑并再次经过点滑到底部,蚂蚁与碗内各处的动摩擦因数均相同且小于,若最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
A. 点与球心的连线与竖直方向的夹角小于
B. 上爬过程中,蚂蚁所受摩擦力逐渐减小
C. 上爬过程中,蚂蚁所受碗的作用力逐渐增大
D. 上爬过程和下滑过程中,蚂蚁经过点时所受支持力相同
如图所示,、和是竖直平面内三根固定的光滑细杆,、、、、位于同一圆周上,为圆周的最高点,为最低点,为圆心。每根杆上都套着一个小滑环未画出,两个滑环从点无初速释放,一个滑环从点无初速释放,用、、分别表示滑环沿、、到达、所用的时间,则下列关系不正确的是( )
A. B. C. D.
如图为竖直面内的一个圆,从圆上最高点到圆上、两个斜面和,斜面与竖直方向夹角为和,物块从点由静止释放,沿经时间到,沿经时间到则( )
A. 若不计摩擦,则
B. 若不计摩擦,则
C. 若有摩擦且动摩擦因数相同,则
D. 若有摩擦且动摩擦因数相同,则
如图所示,倾角为的斜面上有、两点,在点竖直地固定一光滑直杆,点与斜面底端点间置有一光滑的直杆两杆上各穿有一钢球视为质点将两球从点同时由静止释放,分别沿两细杆滑到杆的末端.球由到的时间,球由到的时间不计一切阻力影响,则下列说法正确的是( )
A. 条件不足,无法判断两球运动时间关系
B.
C. 球由到的时间与球由到的时间之比为:
D. 球由到的时间与球由到的时间之比为:
如图所示,位于竖直平面内的固定光滑圆环轨道与水平面相切于点,与竖直墙壁相切于点。竖直墙壁上另一点与点的连线和水平面的夹角为,是圆环轨道的竖直直径的顶点。已知在同一时刻、两球分别由、两点从静止开始沿光滑倾斜直轨道、运动到点,球由点沿着光滑竖直直径自由下落到点,则下列说法正确的是
A. 球最后到达点 B. 球最先到达点
C. 球和球同时且先于球到达点 D. 球和球都可能先到达点
身体素质拓展训练中,人从竖直墙壁的顶点沿光滑杆自由下滑到倾斜的木板上人可看作质点改变木板的倾斜角,人沿着三条不同路径、、滑到木板上的时间分别为、、,已知、、与板的夹角分别为、和,则有( )
A. B. C. D.
如图所示,一倾角很小、高为的斜面固定在水平地面上,光滑小球由斜面顶点从静止开始下滑,到达底端所用时间为如果过、两点将斜面剜成一个圆弧面,使圆弧面点恰与底面相切,该小球由到所用时间为 则 的值为( )
A. B. : C. D.
二、计算题(本大题共3小题,共40.0分)
如图所示,一根内壁光滑的直角三角形玻璃管处于竖直平面内,,让两个小球可视为质点分别从顶点由静止开始出发,一小球沿滑下,到达所用的时间为,另一小球自由下落经到达,所用的时间为,在转弯的处有个极小的光滑圆弧,可确保小球转弯时无机械能损失,且转弯时间可以忽略不计,,求:的值。
如图所示在倾角为的光滑斜面上,有一根直杆,长为距下端处有一点让杆由静止释放,全程杆没有脱离斜面.求:全杆经过点所用时间
跳台滑雪是一项精彩又刺激的运动.如图所示,滑雪运动员从山坡的点由静止开始滑下,从点飞出,最后落在点.已知该
运动员的质量为,、段与水平面夹角为,段水平,在处由一小段圆弧连接.段动摩擦因数为,
长,其余摩擦和空气阻力不计,求:
运动员在段滑下的加速度
运动员在空中飞行的时间
运动员落到点时的速度.
答案和解析
1.【答案】
【解析】
【分析】本题考查了匀变速直线运动的位移与时间的关系、从受力确定运动情况、用牛顿运动定律分析斜面体模型的相关知识,试题难度较易
【解答】设三个光滑斜轨道的共同底边长为,当物体沿着与水平方向成角的斜轨道下滑时,加速度,斜轨道长,物体沿光滑斜轨道下滑的时间由可得当时,,,此时值最小,因此乙最先到达点;当和时,,因此甲和丙滑行的时间相同,在乙之后同时到达点,故C正确.
2.【答案】
【解析】
【分析】
根据牛顿第二定律和匀变速直线运动规律,分别计算出小孩从、、三块滑板到所用的时间进行比较即可。
解决本题的关键是根据牛顿第二定律对物体进行受力分析,并根据匀变速直线运动规律计算出时间。
【解答】
斜面上小孩的加速度:
斜面的长度,
得:,
,
把与水平面的夹角分别代入得:,
,,
知,
即先到,同时到,故B正确,ACD错误。
故选B。
3.【答案】
【解析】
【分析】
根据等时圆模型,可知从圆上最高点沿任意一条弦滑到底所用时间相同,故沿和滑到底的时间相同,不是一条完整的弦,时间最短,长度超过一条弦,时间最长.
如果不假思考,套用结论,就会落入等时圆”的陷阱,要注意点不是最高点,难度适中
【解答】
以为直径画园,根据等时圆模型,对小滑环,受重力和支持力,将重力沿杆的方向和垂直杆的方向正交分解,根据牛顿第二定律得小滑环做初速为零的匀加速直线运动的加速度为为杆与竖直方向的夹角
由图中的直角三角形可知,小滑环的位移
所以,与无关,
可知从圆上最高点沿任意一条弦滑到底所用时间相同,故沿和滑到底的时间相同,即,不是一条完整的弦,时间最短,即,长度超过一条弦,时间最长,即故ABC正确,不正确
因选不正确的,故选:.
4.【答案】
【解析】解:蚂蚁缓慢上爬,可以认为蚂蚁处于平衡状态,则合力始终为零,受力分析,根据共点力平衡有:
,
A、在点恰好滑动,则:
由于小于,所以点与球心的连线与竖直方向的夹角小于故A正确;
B、因为点的与球心的连线与竖直方向的夹角比点的小,所以在点碗对蚂蚁的摩擦力小于在点的摩擦力,在上爬过程中,蚂蚁所受摩擦力逐渐增大,故B错误;
C、在蚂蚁向上爬的过程中,碗对蚂蚁的作用力都等于蚂蚁的重力,所以在上爬过程中,蚂蚁所受碗的作用力不变,故C错误。
D、蚂蚁沿碗下滑的过程中做圆周运动,需要一定的向心力,所以下滑的过程中蚂蚁受到的支持力大。故D错误
故选:。
蚂蚁缓慢上爬,可以认为蚂蚁处于平衡状态,合力为零,蚂蚁所受的摩擦力为静摩擦力,与重力延斜面向下的分力平衡,所以越往上爬,所受静摩擦力越大。
解决本题的关键能够正确地受力分析,运用共点力平衡进行求解。
5.【答案】
【解析】
【分析】
本题关键从众多的杆中抽象出一根杆,假设其与水平方向的夹角为,然后根据牛顿第二定律求出加速度,再根据运动学公式求出时间表达式讨论。
先受力分析后根据牛顿第二定律计算出滑环沿任意一根杆滑动的加速度,然后根据位移时间关系公式计算出时间,对表达式分析,得出时间与各因素的关系后得出结论。
【解答】
解:设与竖直方向的夹角为,由几何关系得与竖直方向的夹角为,环沿下滑时的加速度大小为,
沿下滑时的加速度大小为,
设长为,由几何关系得长为,
根据运动学公式有,,,
得,,
由此得到;由于,同理可得到,因此,,故A错误,符合题意,BCD正确,不符合题意。
故选:。
6.【答案】
【解析】解:设圆的直径为.
A、不计摩擦,取任一路线研究,设斜面与竖直方向的夹角为,则加速度为,位移为
由得,与无关,则得:故AB错误.
C、若有摩擦,设动摩擦因数为,则根据牛顿第二定律得:
由得,则越大,越大,故有故C正确,D错误.
故选:
明确几何关系,根据牛顿第二定律得到加速度,由位移公式表示出运动时间,即可进行比较.
本题关键从众多的杆中抽象出一根杆,假设其与水平方向的夹角为,然后根据牛顿第二定律求出加速度,再根据运动学公式求出时间表达式进行讨论.
7.【答案】
【解析】解:质点沿杆下滑的加速度,位移,由可得:;
质点沿杆下滑,令,则位移,加速度为:
根据位移时间关系有
可得运动时间为:
所以可得::
故选:
根据牛顿第二定律求出加速度的大小,结合位移时间公式求出运动的时间,再进行比较.
解决本题的关键正确地受力分析,运用牛顿第二定律结合运动学公式进行求解,知道加速度是联系力学和运动学的桥梁.
8.【答案】
【解析】
【分析】
根据几何关系分别求出各个轨道的位移,根据牛顿第二定律求出加速度,再根据匀变速直线运动的位移时间公式求出运动的时间,从而比较出到达点的先后顺序。
解决本题的关键根据牛顿第二定律求出各段的加速度,运用匀变速直线运动的位移时间公式进行求解。
【解答】
对于段,位移,加速度,根据得,;
对于段,位移,加速度,由得,;
对于段,位移,加速度,由得,。知最小,故C正确,、、D错误。
故选C。
9.【答案】
【解析】
【分析】
将看做圆的直径,由几何关系判断、、三点与圆周的位置关系,由等时圆的特点解决。
本题主要考查等时圆问题,知道在竖直平面内的圆中,从最高点沿光滑杆滑到圆周上各点用时相等是解题的关键,难度不大。
【解答】
在竖直平面内的圆中,从最高点沿光滑杆滑到圆周上各点用时相等。由题意可知,由于、、与板的夹角分别为、和,故由数学知识可知点在以为直径的圆上,而点在圆外、点在圆内,故可知人沿着三条不同路径、、滑到木板上的时间关系为:,故A正确,BCD错误。
故选A。
10.【答案】
【解析】
【分析】
本题主要考查了物理建模的能力,考查了牛顿第二定律的应用和单摆模型。
要求两种运动时间的比值需要求出两种运动的时间,光滑小球从斜劈顶点由静止开始下滑,做匀加速直线运动,这是一个同学的熟悉的运动模型,应用牛顿运动定律和运动学公式即可求解,但是把斜面剜成圆弧面则不易求解,同学会感觉无从下手,无限分割,变曲为直,数学知识又跟不上,几乎无法求解.但是分析发现剜成圆弧面在点与底面相切,以点为中心,在其右侧补偿一个对称的圆弧面,小球的运动即变成了一个同学们都熟悉的简谐运动模型了,小球沿弧运动的时间为类单摆运动周期的四分之一。
【解答】:
第一种情况,小球做匀加速运动,,第二种情况,小球做简谐运动,时间 ,为圆弧槽的半径,,所以,故A正确,BCD错误。
故选A。
11.【答案】解:设三边分别为、、
第一个小球由滑下时加速度为
由位移时间公式得
解得
第二个小球沿段有
解得
该球到达点的速度大小为
沿水平段运动时有,得
则
故
答:的值为。
【解析】根据牛顿第二定律求出小球沿下滑的加速度,由位移公式求出时间与长度的关系。另一小球在段做自由落体运动,段做匀速直线运动,分别求出两段时间与位移大小的关系,再求解的值。
本题要学会用相同的量表示、,分段运用牛顿第二定律和运动学公式相结合求出时间的表达式,也可以通过作速度时间图象进行分析。
12.【答案】解:对杆受力分析,根据牛顿第二定律可知:,
解得:
到达点时有:,
解得:
点到达点时有:,
解得:
全杆经过点所用时间为:
答:全杆经过点所用时间为
【解析】杆全部通过点需时间为杆的上端到达点的时间减去杆的下端到达点的时间,根据匀加速直线运动的位移时间公式即可求解.
本题考查分析处理匀加速直线运动运动的能力.关键抓住杆全部通过点时间如何理解.
13.【答案】解:段:匀加速直线运动,根据牛顿第二定律可知:
解得:
段:根据速度位移公式有:,
解得:
段:平抛运动为:
在水平方向上有:
在竖直方向上有:
联立解得:
在段做平抛运动,则有:
故D点速度为:
答:运动员在段滑下的加速度为
运动员在空中飞行的时间为
运动员落到点时的速度为
【解析】根据牛顿第二定律求得下滑的加速度;
从点做平抛运动,根据平抛运动的特点求得运动时间和速度
本题考查了求运动员的落点位置,分析清楚运动员的运动过程,应用平抛运动规律即可正确解题,解题时注意数学知识的应用.
第1页,共1页
